基于电磁力反馈的磁浮列车悬浮控制方法

郭 维，侯招文，徐绍龙，甘韦韦，王文韬，陈启会

（株洲中车时代电气股份有限公司，湖南 株洲 412001）

0 引言

磁浮列车的悬浮系统一般可分为电磁吸力悬浮（electrical magnetic suspension，EMS）式、超导电动斥力悬浮式和永久磁铁悬浮式3 种[1]，目前广为应用的是EMS 型悬浮系统，其不仅可应用于中低速磁浮列车，也能应用于高速磁浮列车。EMS 型悬浮系统的工作原理是通过调节悬浮电磁铁中的电流来调节电磁铁与轨道之间的吸引力，使列车稳定悬浮，与轨道保持一定的间隙。该间隙距离一般为8～12 mm，且列车速度越快，悬浮间隙越大。

目前主流的悬浮控制算法采用“间隙外环-电流内环”的双环控制结构[2-3]。其中，间隙外环根据间隙给定值、间隙反馈值以及加速度值计算电磁铁所需要的电流值；电流内环则是通过控制电磁铁两端的电压使电流快速跟随间隙外环计算的电流给定值，这两个控制环节均采用比例-积分-微分（proportionalintegral-derivative, PID）控制器。这种悬浮控制方法物理意义明确，鲁棒性强，但由于其是根据平衡点附近的线性化模型得到的，一旦系统离开平衡点，则难以保证控制性能[4]，容易引起高频抖动，且在阶跃响应时也容易引起超调；同时PID 控制器的参数范围较窄，难以获取优良的控制性能[5]。为此，诸多学者和科研人员提出了一些优化和改进的方法：陈强、李晓龙等将非线性PID 控制引入到磁浮列车的悬浮系统中，有效改善了传统线性PID 控制的静态和动态性能、跟踪设定值与抑制扰动之间的矛盾[6]；李晓龙、张志洲等深入研究了悬浮控制系统中的信号处理算法，为悬浮控制性能的进一步优化提供了算法基础[7-8]；朱付景、刘恒坤等优化了双环控制中微分信号的获取方法，提高了悬浮控制系统性能，减少了车轨耦合振动现象[9-10]；Danfeng Zhou，Jie Li 等分析了磁浮列车悬浮间隙存在低频波动的原因，并提出了抑制低频波动的方法[11-12]。但这类方法都存在控制参数稳定范围小、参数调试难度大的缺点。

根据电磁铁电磁力和磁通的关系可知，只要控制悬浮电磁铁中的磁通，就能控制悬浮电磁铁的电磁力，最终控制悬浮间隙，因此悬浮控制算法中的电流环也可被替换为磁通环。英国Roger Goodall 提出将电流内环替换为磁通内环，并成功应用于工程实践[13]。孙明秋[14]、张文清[5]等对基于磁通反馈的方法进行了改进和优化，结果表明基于磁通反馈的方法具有参数易于调试、参数稳定范围大、控制带宽较窄、抗干扰能力强等优点，但是这类方法需要悬浮用磁通传感器，而这类传感器设计难度高，目前还难以满足工程化需求。

悬浮控制最终是通过控制电磁铁的悬浮力来控制悬浮间隙，因此可在悬浮控制中加入电磁力控制环节。为此，本文提出一种电磁力反馈的方法，其通过间隙控制器得到电磁铁需要产生的悬浮力，根据电磁力控制环节获得电磁铁产生该悬浮力所需要的电流，最终利用电流环实现该电流的输出。实验结果表明，采用该方法，容易获取满足工程运用的控制参数，且容易获得悬浮系统期望的阶跃响应时无超调的效果，具有进一步研究和工程应用的价值。

1 磁浮列车的单电磁铁模型

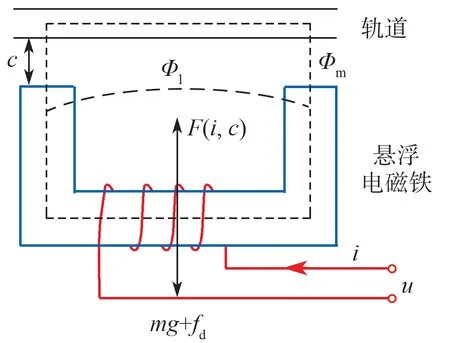
图 1 单电磁铁模型示意图Fig. 1 Schematic diagram of single-electromagnet model

磁浮列车是一个多点悬浮系统，通过机械解耦后，磁浮列车的悬浮控制问题可被简化为单个电磁铁的悬浮控制问题。单电磁铁模型示意如图 1 所示[15]。图中，c为电磁铁磁极与轨道之间的距离；u,i分别为电磁铁两端的电压和流过电磁铁中的电流；Φ m,Φ l分别为气隙磁链和漏磁链；F(i,c)为电磁铁与轨道之间的电磁吸引力；fd(t)为外部扰动力。

忽略漏磁、磁路饱和以及电磁铁和轨道中的磁阻，并假定电磁铁仅有垂直方向位移，则单电磁铁模型可被表述为

式中：m——悬浮模块的质量；g——重力加速度；μ0——真空磁导率；N——电磁铁线圈匝数；A——铁心的有效截面积；R——线圈电阻；k——电磁力系数。

式（1）表明，电磁铁模型为一个非线性系统。当电磁铁悬浮在平衡点(i0,c0)附近时，可通过展开泰勒公式并忽略高阶小项的方式得到式（1）的线性化形式：

式中：s——拉普拉斯变换中的微分算子。

最终得到的系统特征方程为

系统特征方程中的系数存在负数。根据劳斯判据可知，该系统为一个不稳定系统，因此需要进行闭环反馈才能实现系统的稳定控制。

2 基于电磁力反馈的悬浮控制算法

经典悬浮控制算法采用“间隙外环-电流内环”的双环控制结构，其典型结构如图 2 所示。间隙控制器和电流控制器均采用PID 控制器。为了减少间隙微分带来的噪声影响，间隙控制器的微分部分常通过加速度积分的方式获得（图2 中a表示电磁铁的加速度）。该方法物理意义清晰，但在施加干扰或阶跃响应时容易产生超调。虽然可通过各种手段进行优化，但在工程实践中发现难于找到最优参数，存在调试困难等缺点。

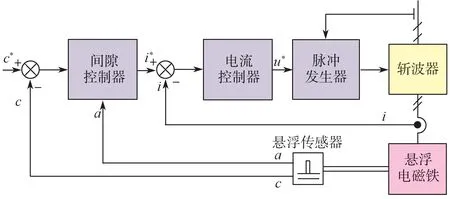
图 2 双环悬浮控制算法框图Fig. 2 Block diagram of the double-loop levitation control algorithm

悬浮控制的最终目的是控制电磁铁和轨道之间的间隙，其最终实现手段是控制电磁铁与轨道之间的电磁吸引力，因此可在间隙控制器和电流控制器之间增加电磁力控制环节，使电磁铁快速产生系统所需的悬浮电磁力，对应的控制算法原理如图 3 所示。间隙控制器根据实际间隙c和给定间隙c*产生电磁铁所需要的电磁力，并将其作为电磁力控制器的给定。本文中的间隙控制器采用PID 控制器，则给定电磁力的表达式可写为

式中：Kpc,KIc,Kdc——间隙控制的比例增益、积分增益和微分增益。

图 3 基于电磁力反馈的悬浮控制算法Fig. 3 Levitation control algorithm based on electromagnetic force feedback

电磁力控制器根据给定电磁力F*（间隙控制器输出）和实际电磁力F（悬浮力观测器输出）得到电磁铁所需要的电流i*（电流给定值），并通过电流控制器实现对该电流的快速跟踪。由于电磁铁和轨道之间的悬浮力（吸引力）无法被测量，因此实际悬浮力可通过当前间隙、当前电流以及电磁铁的参数计算得到，计算表达式如式（1）所示。

在实际应用中，为了简化参数调试难度，电磁力控制器和电流控制器均可使用比例-积分（或比例）控制器替代PID 控制器，故本文中的电磁力控制器和电流控制器均采用比例-积分控制器。电磁力控制器和电流控制器表达式为

式中：Kpf,KIf——电磁力控制器的比例和积分增益；Kpi,KIi——电流控制器的比例和积分增益。

3 实验研究与结果

3.1 实验平台

为了验证上述基于电磁力反馈的悬浮控制算法，搭建了一套小型悬浮控制系统（图 4）。系统主要由可调直流电源提供直流母线电压，DSP（TMS320F28335）为其核心控制芯片，由MOSFET 作为半H 桥功率电路的器件。悬浮控制系统对应的实物如图 5 所示。图中的上、下轨道是固定的，悬浮电磁铁安装在上、下轨道上，中间轨道是活动的，在电磁铁的吸引力和重力的相互作用下能够实现垂向运动。该实验平台不仅能够用于悬浮控制，也能用于导向控制研究。

图 4 悬浮实验平台示意Fig. 4 Schematic diagram of the levitation experimental platform

图 5 悬浮实验平台实物图Fig. 5 Physical picture of the levitation experimental platform

悬浮电磁铁的主要参数如表1 所示。

表 1 单铁悬浮平台参数Tab. 1 Parameters of the single-electromagnet levitation platform

3.2 控制系统实现与参数设定

悬浮控制系统采用TMS320F28335 型控制芯片，其最高运行频率可到150 MHz。由于悬浮系统是一个开环不稳定系统，若控制器的控制周期太长，则系统容易发散；但如果控制周期过短，则控制芯片可能在一个周期内无法运行完全部程序，更重要的是，电磁铁本身是一个电感，其时间常数较大，电磁铁产生的电流无法快速响应控制器的输出，且过高的开关频率会使电力电子器件的损耗加大。因此，综合考虑以上各因素，设定控制器的控制周期为200 μs，电力电子器件（MOSFET 管）的开关频率为5 kHz。

为了简化控制器参数数量，电磁力控制器和电流控制器均采用PI 控制器，间隙控制器采用PID 控制器。一般工程应用中，间隙控制器的微分项通过加速度积分计算获得。加入了电磁力控制器后，通过对间隙进行微分计算也能获得良好的控制性能，因此本实验中未采集加速度信号。为了降低间隙微分计算带来的噪声，微分环节采用不完全微分，其离散形式表达式为

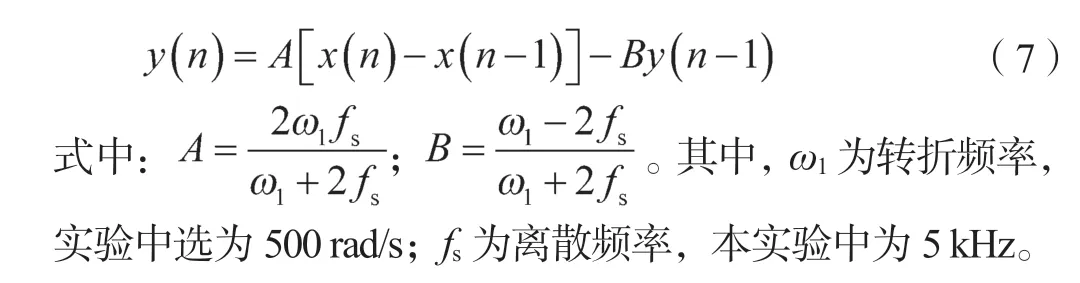
在调试过程中，可由内到外逐环调试。内环主要考虑快速性。首先，断开电磁力控制器环节，直接施加电流阶跃给定信号（需注意该给定信号应比起浮电流小，否则悬浮电磁铁产生的悬浮力将大于其重力，会致使电磁铁快速撞向轨道），调节电流控制器的PI 参数，使电流输出能较快跟踪电流给定值。接着，断开间隙环，直接进行电磁力阶跃给定，调节电磁力控制器的比例和积分增益，使电磁力控制器的输出能快速跟踪电磁力控制器的输入。为了避免出现分母为零的情况，对悬浮力观测器中用于估算电磁力的间隙最小值进行了限幅处理（间隙最小值为0.5 mm）。最后，再调试最外环间隙控制器的控制参数。在基本调试成功后，可对3 个控制环节的参数进行微调，使控制效果最佳。参数调节过程如图6 所示。

图6 控制器参数调节方法Fig. 6 Controller parameter adjustment method

实践证明，基于电磁力反馈的悬浮控制系统的参数较为容易获得。经调试，得到一组控制参数如表 2 所示。

表2 控制器参数Tab. 2 Parameters of the controllers

3.3 实验结果

为了验证本文所提控制算法的性能，在图 5 所示悬浮实验样机平台上进行了测试。图7 示出直流母线电压为36 V、给定间隙为8 mm 时的阶跃响应波形。图中，CH1 通道为电流波形（2.15 A/div），CH2 通道为间隙波形（2 mm/div），CH3 和CH4 通道为运动部分（图5）能够达到的上、下限（即最大和最小间隙值）。由于示波器无法直接采集电流和间隙信号，因此电流信号和间隙信号是根据采样电阻的电压换算得到的，即示波器上CH1 通道的500 mV 表示2.15 A，CH2 通道的2.00 V 表示2 mm。由图可见，阶跃起浮时，系统基本无超调且能够较快地达到给定间隙（起浮过程中间隙是减小的）。图 8为悬浮系统缓降波形（各通道参数同图7），可见，缓降过程中，间隙逐步增加，未出现冲击现象。

图 7 给定间隙为8 mm 时的阶跃响应波形Fig. 7 Step response waveform when the gap reference is 8 mm

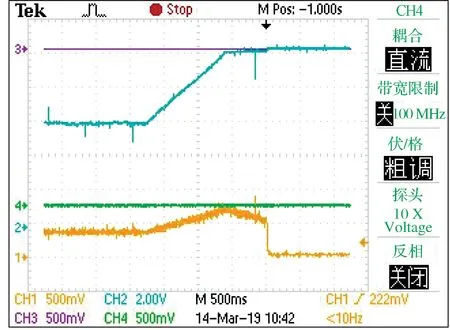
图 8 缓降波形Fig. 8 Slow drop waveform

图 9 和图10 为施加外力干扰使中间轨道撞击上、下轨道后的输出波形（各通道参数同图7）。可以看到，当外力消失后，系统能够以接近临界阻尼的状态返回至给定的8 mm 间隙处。该特性是设计磁浮列车悬浮控制系统时所期望的：即使在外界干扰下列车撞击了轨道，也不会出现来回多次撞轨的现象。

图9 向下施加外力前后输出波形Fig. 9 Output waveforms of the system with and without an external downward force

图 10 向上施加外力前后输出波形Fig. 10 Output waveforms of the system with and without an external upward force

图 11 和图 12 分别为在间隙给定中施加幅值为2 mm、时长为1 s 的正负脉冲干扰后的结果（图中各通道参数同图7）。可以看到，当间隙给定从8 mm →10 mm →8 mm（图10）以及8 mm →6 mm →8 mm（图12）变化过程中，悬浮系统能够快速跟踪相应的给定值，且该过程中超调不超过0.2 mm。在干扰结束后，系统也能够快速回到8 mm 给定间隙处。

图 11 间隙给定中叠加2 mm 正脉冲干扰时的结果Fig. 11 Result for a 2 mm positive pulse interference in the reference gap

图 12 间隙给定中叠加2 mm 负脉冲干扰时的结果Fig. 12 Result for a 2 mm negative pulse interference in the reference gap

图 13 和图 14 示出不同给定间隙时的控制效果。可见，本文所提方法在不同间隙处均能够实现稳定悬浮，且阶跃响应时超调不超过0.2 mm。

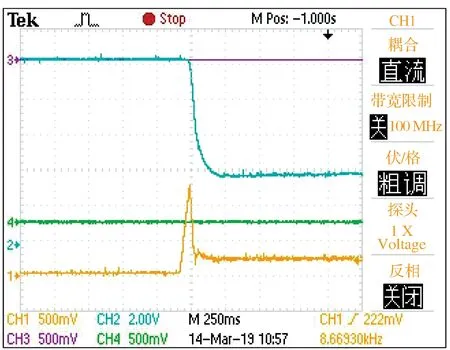
图 13 给定间隙为6 mm 时的阶跃响应波形Fig. 13 Step response waveform when the gap reference is 6 mm

图 14 给定间隙为10 mm 时的阶跃响应波形Fig. 14 Step response waveform when the gap reference is 10 mm

为了验证该算法的鲁棒性，测试该算法在不同直流母线下的效果。将直流母线电压降低1/3（母线电压 24 V），间隙给定为8 mm 时的阶跃响应波形如图 15所示。对比图 7（母线电压36 V）结果可知，母线电压降低时系统仍能够正常悬浮，但是在电压较低时达到给定间隙处的时间稍长。

图 15 直流母线电压降为24 V、给定间隙8 mm 时的阶跃响应波形Fig. 15 Step response waveform when the gap reference is 8 mm and Udc is 24 V

在实际工程应用中，一般难以获得表 1 中部分参数的准确值，特别是磁极的有效截面积，其会受车辆运行状况的影响。当车辆偏离轨道时，磁极的有效截面积将发生变化，因此利用式（1）观测出的电磁力存在误差。根据表 1 中的参数，计算出电磁力系数k=1.49×10-3。图 7～图 15 均是k=1.49×10-3时的结果。为了验证该电磁力系数对控制效果的影响，将电磁力系数减半，即k=7.45×10-4，其结果如图 16 所示。对比图 7 可知，电磁力系数误差对本文所提方法的影响很小。因此，即便表1 中部分参数存在偏差，也不会明显影响系统的控制性能，这表明本文所提方法具有较好的鲁棒性。

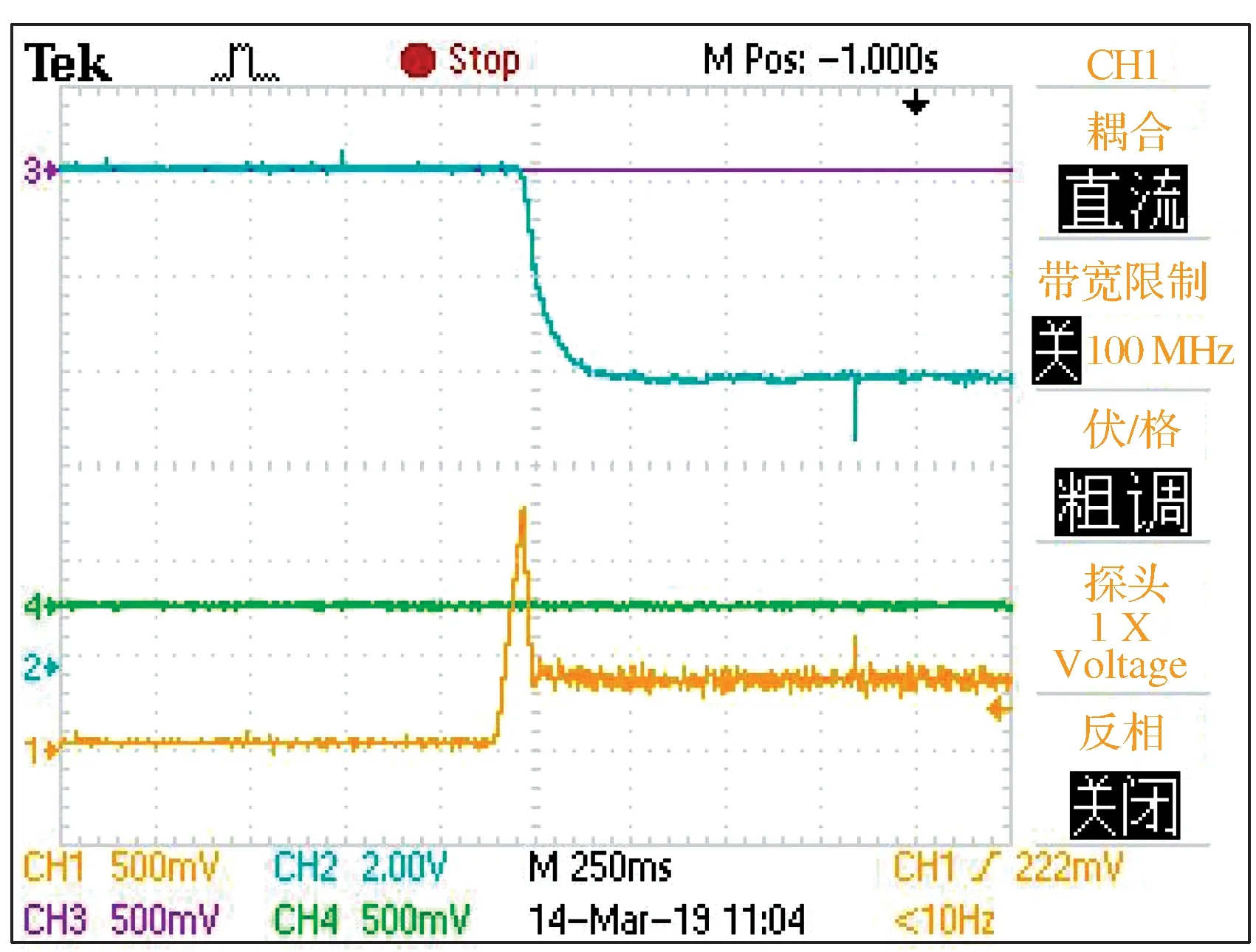
图 16 电磁力系数减半、给定间隙为8mm时的阶跃响应波形Fig. 16 Step response waveforms when the gap reference is 8 mm and the electromagnetic force coefficient is halved

4 结语

本文提出一种基于电磁力反馈的悬浮控制方法，其具有以下优点：（1）在不同的给定间隙下，其阶跃响应的超调都很小，大部分工况下可实现无超调控制，控制效果优，当给定间隙存在阶跃变化时，系统能够快速恢复稳定；（2）施加外力使车辆撞击轨道后，一旦干扰消失，系统能够以准临界阻尼方式回到给定位置处，说明系统足够稳定，不会来回撞击轨道，该特性符合磁浮列车的需求；（3）系统的鲁棒性较强，当电源电压变化或者控制系统所用参数与实际系统存在偏差时，系统仍具备良好的控制效果，且参数调试较为简单。

本文所提方法具备工程化应用价值。但是，该方法在磁浮列车过弯道、上下坡、过接缝等特殊工况以及轨道不平顺等条件下的性能仍有待进一步检验。后续将在转向架和整车上对该算法进行优化并验证该算法的效果。