变给定增益PI控制策略的设计仿真*
2019-09-27叶婷
叶 婷
(西安航空职业技术学院 西安 710089)
1 引言
尽管永磁同步电动机转速环利用IP控制可以有效抑制阶跃响应的超调,但同时会造成系统的动态响应速度变差。传统的提高跟踪性能的方法是增大控制器带宽参数,而这又会导致系统的噪声变大。为解决这一问题,本文在IP控制器的基础上,将给定信号经一个增益后加入到控制量中,通过改变增益可以使IP控制切换至变为PI控制。本文找到了一个最优增益,可实现阶跃响应无超调的同时使系统的跟踪性能最好,定义此时的控制器为最优IP控制器。同样,为提高控制器对多种输入的适应性,本文提出了一种变给定增益PI控制策略。
2 最优PI控制器
为了使得转速控制系统的阶跃输入响应无超调的同时,提高响应的快速性,在此设计了如图1的带给定增益的PI控制器。
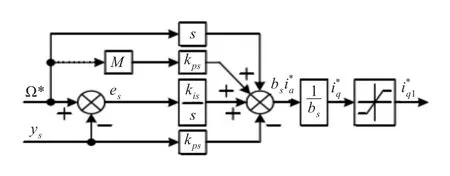
图1 带给定增益的PI控制器
由图1可制,被控量i*q为
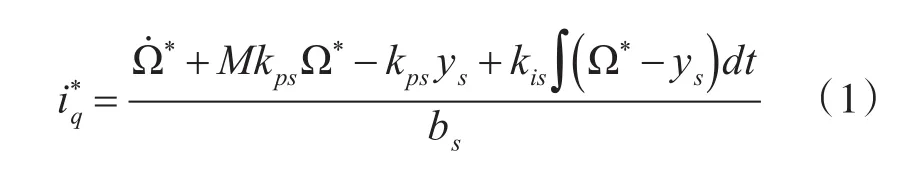
式中:kps为控制器的比例系数;kis为控制器的积分系数;bs为控制增益;为交轴电流给定值;Ω为机械角速度;ys为机械角速度的测量值;M为给定增益。
不考虑控制量饱和、反馈转速滤波、电流环带宽的影响,将式(1)代入式机械角速度的状态方程,可得系统的输出为
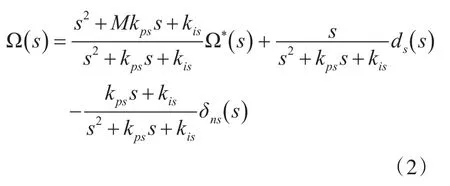
特别地,当M=0时,控制系统可等效为IP系统,当M=1时,可等效为PI控制系统。
系统输入为阶跃信号,输出将变为
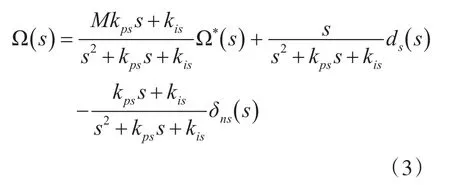

由式4可知,当M>0.5时,超调量σ%只与M的取值有关,二者成正比的关系。
取ωn=80、ζ=1,则kps=160、kis=6400,系统跟踪连续变化输入的频域特性曲线见图2。
据此可知,M的取值变小,系统的响应快速性也变差,再结合前面的得出的结论,阶跃响应无超调的条件0≤M≤0.5,得出最佳的M的取值为0.5。
M=0.5,系统的传递函数为

由式(5)可知,此时的系统为一阶惯性环节,定义此时的控制器为最优IP控制器。
由此可得,当M分别为0、0.5、1时,系统分别输入四种不同输入信号时的传递函数如表1所示。

图2 系统跟踪连续变化输入的频域特性曲线

表1 IP、最优IP和PI三种控制系统的性能对比
由表1可知,在不改变系统抑制噪声性能和抗干扰性能的前提下,当输入为连续变化信号时,M=1系统的跟踪性能最佳;当输入为阶跃信号时,M=0.5系统则能够获得最佳的性能。故对于带给定增益的PI控制系统而言,可根据输入信号的变化来选取相应的M值,以获得最佳的性能。
3 变给定增益PI控制器
基于前面的分析,为了实系统在阶跃输入信号和连续变化输入信号两种情况下均获得最佳响应性能,设计了结构如图3所示的变给定增益的PI控制器。
它能够根据给定变化率推断输入信号类型,并据此选取合适的增益M,当连续变化信号给定的变化率在首个周期之后不恒为0,此时M取值为1,能够完成系统对连续变化输入信号的优良响应;阶跃信号给定的变化率在首个控制周期之后恒为0,此时M取为0.5,则可完成系统良好的阶跃响应。

图3 变给定增益PI控制器
4 仿真分析
4.1 系统的输出响应仿真
1)阶跃输入信号响应
M分别取0、0.5和1,阶跃输入分别为80r/min和800r/min的空载起动,此时响应波形如图4(a)、(b)所示。由仿真波形可知,当M=0.5时,在系统的快速性及超调方面能够获得最佳的性能。

图4 阶跃输入信号的响应曲线
2)正弦输入信号响应
同理M分别取0、0.5和1,输入500rpm/5Hz的正弦信号时,响应波形见图5。
由仿真结果可知,M依次取0、0.5和1时,系统对应的响应误差为370r/min、160r/min和4r/min。故当M=1时,能够获得最佳的跟踪性能。
3)输入信号切换响应
当输入信号由阶跃切换至正弦,再由正弦切换至阶跃时,系统的响应曲线如图6所示。由图可知,控制系统的输出响应能够很好地跟踪输入信号的变化。
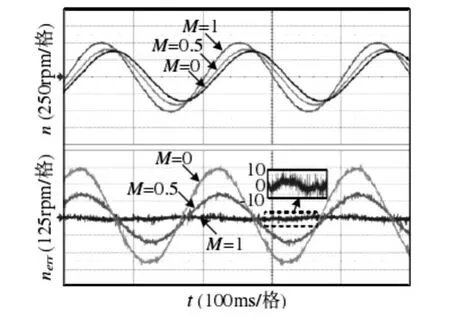
图5 正弦输入信号的响应曲线
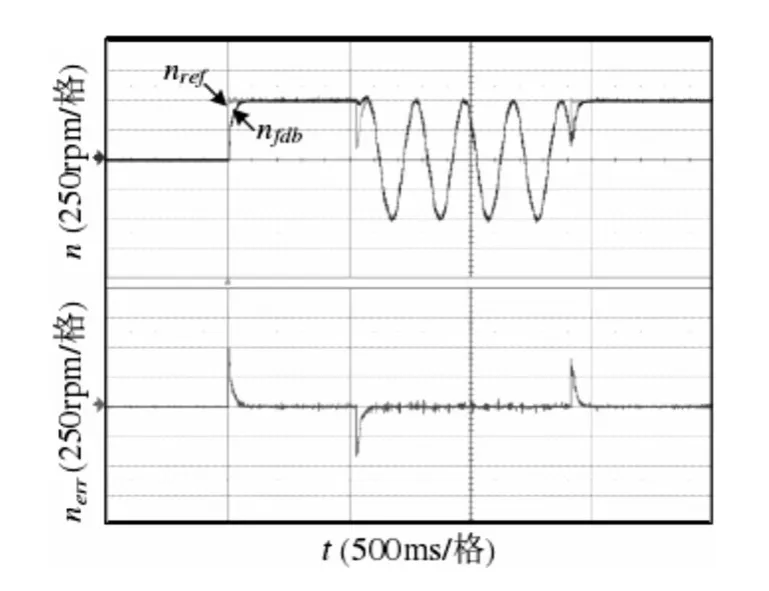
图6 输入信号切换时的转速响应
4.2 系统的抗干扰性仿真
为了证实系统的抗干扰性能,在阶跃信号作用下,电动机先以800r/min的转速空载运行,然后对负载按图7曲线所示进行加载和卸载。当M取值分别0、0.5、1时,加载和卸载过程获得的仿真曲线依次见图8(a)和(b)。由图可知,不论是加载还是卸载过程,三种不同情况下的仿真曲线完全一致,这恰恰证实了系统的抗干扰性与M取值无关的理论。
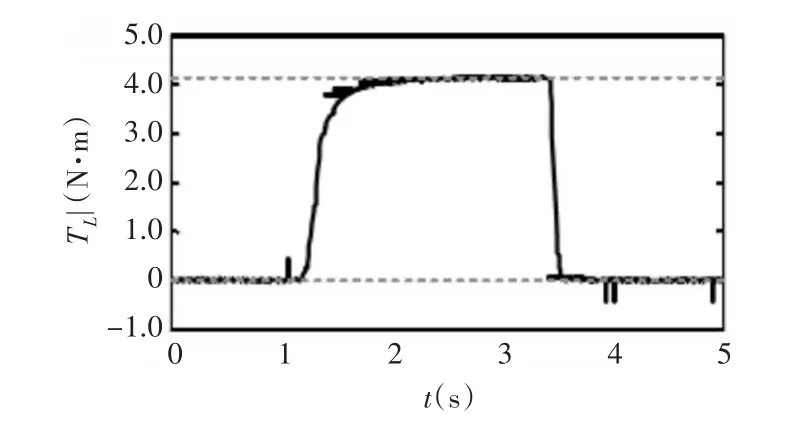
图7 实验负载曲线
5 结语
本文设计的变给定增益PI控制器,通过给定增益M的引入,能够根据输入信号给定变化率确定信号类型,并据此自动选取对应的最佳增益,从而在IP控制和PI控制之间架起了桥梁,最终使系统在不同的输入信号作用下均能获得很好的跟踪性能。
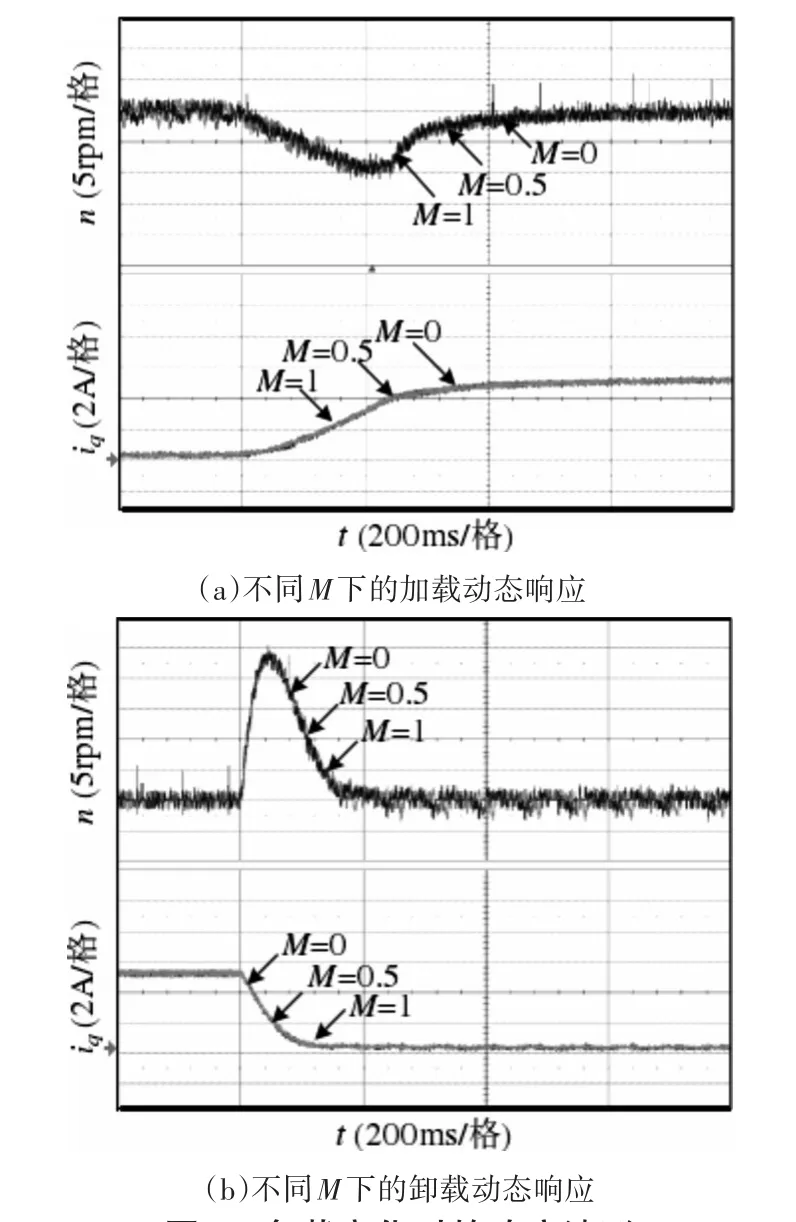
图8 负载变化时的响应波形
