基于样本外预测的GARCH族模型评价研究
2020-02-21张胜杰
张胜杰


摘 要:对金融资产的波动率预测,GARCH族模型是主流的参数法模型。现有研究主要采用样本内回测进行模型评价,较少运用滚动时间窗或迭代时间窗的样本外预测来进行评价比较。以沪深300指数为研究对象,经过试拟合后建立七种GARCH族模型,采用四种预测精度评价指标,将预测方式由传统的样本内回测扩展为样本外静态、滚动、迭代预测,进行预测能力评价。研究表明,传统方法选择的样本内最优模型未必取得最优的预测效果。因此,在对GARCH族模型选择过程中,应进行样本外预测评价,适时调整模型形式;对于较大的训练样本而言,采用静态预测方式即可取得较好的样本外预测效果,而滚动与迭代预测并未明显提高预测精度。
关键词:GARCH模型;预测能力评价;样本外预测
中图分类号:F830.91 文献标志码:A 文章编号:1673-291X(2020)36-0058-04
引言
金融资产波动率往往具有时变性、聚集性等波动特性,GARCH族模型由于估计简单、拟合较好、易于解释,是主流的参数法模型。Engle(1982)提出ARCH模型,考虑了方差的时变性,将条件方差设定为过去残差平方的函数[1]。Bollerslev(1986)将高阶ARCH模型扩展为低阶GARCH模型,将条件方差设定为过去残差平方及过去条件方差的函数[2]。Engle和Bollerslev(1986)[3]随后又建立IGARCH模型,拟合波动冲击的持续性。此后GARCH族模型获得了持续扩展与应用。J.P.Morgan建立基于Risk Metrics模型的VaR风险度量,该模型利用指数加权移动平均法(EWMA)估计条件波动,其实质为扰动项服从正态分布、简化参数的IGARCH(1,1)模型。Nelson(1991)证明了对于金融资产收益率序列,采用任何一类GARCH模型,即使存在设定错误,但当样本容量充分大时,也能得到条件波动的一致估计[4]。近年来,国内外研究学者Liu[5](2011)、张路胶[6](2006)、张术林[7](2009)、方立兵[8](2014)、吴俊[9](2015)等通过建立GARCH族模型对金融资产的波动率进行拟合,并进行衍生品定价、VaR预测、精度评价等实证研究。大量实证表明,GARCH族模型及其各种扩展形式能成功刻画金融时间序列的这些波动特征。
在传统分析中,把所有样本数据用于模型估计,有利于得到最好的拟合结果,但不利于模型检验和评价,无法检验参数的不变性、模型变量关系的稳定性等,也难以评估预测效果;对GARCH族模型的拟合效果评价,主要采取基于损失函数或VaR超出率的样本内回测评价,较少见到运用动态滚动时间窗或迭代时间窗的样本外预测结果进行评价;而且,对不同模型形式和分布假设的横向比较也研究较少。而White的研究指出,基于样本外预测结果的计量模型评价结论比基于样本内结果更加稳定与可靠[10]。
对此,本文扩展预测方式,进行样本外预测能力的评价研究,主要创新点在于:一是采用样本外预测方式进行模型评价。把整个样本观测区间分为样本内(insample)和样本外(outofsample)两部分,前者用于模型拟合,后者用于预测能力评价。除了采取传统的样本内回测(backtesting)之外,将预测方式扩展为样本外静态(static)、样本外滚动(rolling)、样本外迭代(recursive)预测,进行模型预测能力比较。二是建立多个模型进行横向比较。经过试拟合,波动率不存在风险溢价效应和杠杆效应,但存在持续效应,因此建立GARCH、IGARCH及Risk Metrics三类模型;对于扰动项的分布,考虑到收益率分布的尖峰厚尾特征,采取国内外学者常用的正态、t、GED等三种假设,最终建立GARCH-N、GARCH-GED、GARCH-t、IGARCH-N、IGARCH-GED、IGARCH-t以及RiskMetrics(即EWMA-N)等七种模型进行横向比较。
一、条件波动率模型简介
(一)GARCH模型
GARCH模型可以看作是无限阶的ARCH模型,能够较好刻画波动的持久性,通常,GARCH(1,1)模型即可具有较好的拟合效果。模型如下:
(二)IGARCH模型
(三)Risk Metrics模型
其实质是建立扰动项服从正态分布的EWMA模型来拟合条件波动,下文统称EWMA-N模型,模型如下:
二、实证分析
(一)研究变量及样本数据说明
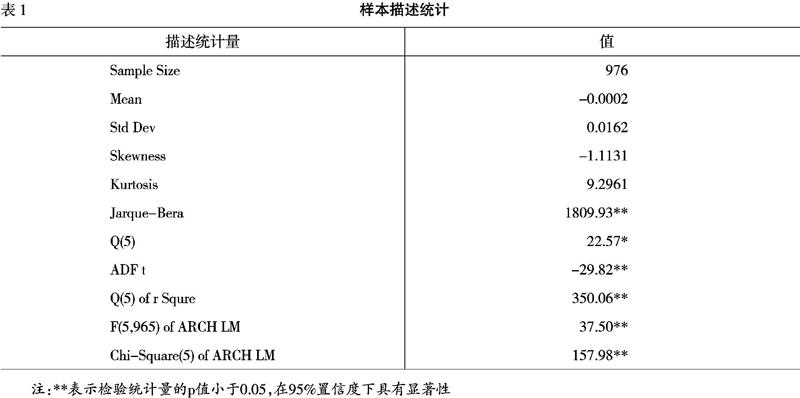
在我国,沪深300指数由大盘蓝筹股构成,代表性强、关注度高,本文选取沪深300指数作为研究变量,为消除除权除息影响,指数价格为向前复权收盘价,第t日收盘价Pt做对数和差分变换,得到日对数收益率序列rt=lnPt-lnPt-1。样本数据的时间范围是2014—2018年,共得到日对数收益率的1 219个观测值。把整个样本观测区间分为样本内(in sample,即训练集)和样本外(out of sample,即测试集)两部分:2014—2017年数据为训练集,样本容量为976,用于模型估计和传统的样本内回测;2018年数据为预测集,样本容量为243,用于样本外预测和模型评价。
整个样本的时序图(如下图所示),其中前974个样本点为样本内数据,用于下文的描述统计、模型参数估计与样本内回测评价。
(二)样本数据描述统计
样本数据的描述统计表(如表1所示),主要统计特征为:均值接近零、略微左偏、尖峰厚尾;JB检验拒绝正态分布假设;ADF检验拒绝存在单位根的原假设,即认为收益率序列是宽平稳的。序列自相关检验中,滞后1阶Ljung-BoxQ统计量不显著、但滞后5阶Ljung-BoxQ统计量具有显著性,因此认为收益率序列不存在明顯的短期自相关性,也反映出我国A股市场基本是弱式有效的,故对条件均值建立ARMA(0,0)模型,即不考虑其自相关性,只保留常数项作为无条件均值。
进一步地,对ARMA模型的残差平方序列进行自相关检验,滞后5阶的Ljung-BoxQ统计量均具有显著性;对ARMA模型的残差序列进行ARCHLM检验,滞后阶数为5时,F与Chi-Square统计量均具有显著性,说明收益率序列存在ARCH效应,可以建立GARCH族模型对条件方差进行拟合。
(三)模型参数估计
在确定并估计模型前,对可能的模型形式进行试拟合。首先,拟合GARCH-M模型,条件均值模型中的方差项系数不显著,认为不存在风险溢价效应;其次,拟合TGARCH模型和EGARCH模型,非对称项系数不显著,认为条件波动不存在杠杆效应;随后,拟合GARCH模型,ARCH项系数与GARCH项系数估计值之和非常接近1,认为波动率受冲击影响持久,可以建立IGARCH模型。对于扰动项的分布假设,考虑到收益率序列的尖峰厚尾特征,采取国内外学者常用的Normal、t、GED等三种分布假设。最终,建立GARCH、IGARCH模型及Risk Metrics模型,结合扰动项的三种分布假设,共建立GARCH-N、GARCH-t、GARCH-GED、IGARCH-N、IGARCH-t、IGARCH-GED、EWMA-N等七种模型,进行参数估计、预测评价和比对分析。模型估计结果(如表2所示)。
(四)模型预测能力评价
为准确评价上述模型的预测效果,按照预测误差最小原则,进行模型预测能力评价。采用样本内回测、样本外静态预测、样本外滚动预测、样本外迭代预测等四种方式,对7个模型进行预测能力评价与比较。
样本内回测(Backtesting),就是用所估模型对样本内数据进行拟合,得到条件方差的拟合值。样本外静态预测(Static Forecasting),就是用样本内数据估计模型后,不再重估模型,用所估模型对样本外数据进行预测,每次采用最新观测数据向前预测一步,共估计1次、预测243次,得到样本外数据的条件方差预测值。样本外滚动预测(Rolling Forecasting),就是用样本内数据作为初始训练集,估计模型并向前预测下一个条件方差,对于样本外数据,以后每次将样本观测窗口向样本外移动一期、保持样本容量不变,重估模型并进一步预测,共重估和预测243次,得到样本外数据的条件方差预测值。样本外迭代预测(Recursive Forecasting),与样本外滚动预测的区别是,每次预测时观测窗口为当日及之前全部数据,即样本容量增加一个数据,共重估和预测243次,得到样本外数据的条件方差预测值。
为做出准确判断,使用平均绝对误差MAE、均方根误差RMSE、Theil不等系数TIC、偏差率BP等四项指标作为预测能力评价指标,越小表明预测值与观测值之间的差异越小,预测精度越高。上述四种预测方式计算出条件方差的预测值后,与相应观测值比较,分别计算出七种模型的预测评价指标。
结语
首先,从模型形式上看。总体上,对于样本内回测,无论是依据传统的似然函数、信息准则,还是评价指标,GARCH-GED是最优模型,尤其是BP指标几乎为零,反映出波动率拟合的无偏性。这主要是由于GED相比正态、t分布能够更好地刻画厚尾特性。对于样本外预测,无论采取静态、滚动还是迭代的预测方式。总体上看,EWMA-N模型取得了最优的预测效果,主要是由于EWMA-N模型实质为漂移项为零的IGARCH模型,能更好刻画波动冲击的持续与衰减特性。样本外最优预测模型与样本内不同,这一现象说明,传统的样本内最优模型未必取得最优的预测效果,对GARCH族模型选择过程中,应考虑样本外预测,对模型形式进行适时调整。
其次,从预测方式上看。对七种模型而言,样本外静态预测均呈现较优的预测效果,而滚动、迭代预测效果并未明显提高。主要原因是,滚动、迭代预测方式虽然逐日重估模型,但样本内容量较大,导致样本外重估并预测的效果并未明显改善,也反映出沪深300指数的波动特性具有稳定性,若研究者进行短期的波动预测,采用静态预测方式即可取得较好效果。
参考文献:
[1] Engle R. F.Autoregressive conditional heteroscedasticity with estimates of the variance of UK inflation [J].Econometrica,1982,(50):987-1008.
[2] Bollerslev T.Generalized autoregressive conditional heteroscedasticity[J].Journal of Econometrics,1986,(31):307-327.
[3] R.F.Engle, T.Bollerslev.Modelling the persistence of conditional variances[J].Econometric Reviews, 1986,(1):1-50.
[4] Nelson D. B.Filtering,Forecasting with Misspecified ARCH Models I:Getting the Right Variance with the Wrong Model[J].Journal of Econometrics,1992,(4):61-90.
[5] LIU H. C.,HUNG J. C.Forecasting S&P-100 stock index volatility:the role of volatility asymmetry and distributional assumption in GARCH models[J].Expert Systems with Applications,2010,(7):4928-4934.
[6] 張路胶,赵华.中国股市波动率的非对称性[J]统计与决策,2006,(20):80-82.
[7] 张术林,魏正红.Risk Metrics模型评估与扩展[J].数学的实践与认识,2009,(5):34-41.
[8] 方立兵,郭炳伸,曾勇.偏斜参数对GARCH族模型估计与预测绩效的影响[J].统计研究,2014,(10):106-112.
[9] 吴俊,杨继旺.上海银行间同业拆放市场杠杆效应——基于GARCH族模型的比较研究[J].管理现代化,2015,(1):4-6.
[10] White, H.A reality check for data snooping[J].Econometrica,2000,(3):1097-1126.
