理解函数概念培养核心素养

连培建

摘要：函数是研究变量之间的关系，在现实中非常有价值，但函数的概念比较抽象，要借助现实背景，在现实情景中理解函数的概念，而在分析和解决问题中，要关注函数概念的数学本质，感悟数学思维，培养数学核心素养，

关键词：函数概念;数学本质;核心素养

数学概念是数学知识的细胞，是一章或一课内容的起始，由于数学概念具有高度的概括性和抽象性，学生较难理解把握，在教学中，教师一般能遵循从直观到抽象，再逐渐具体化、形象化，但在概念教学中要努力揭示概念的发展和本质，力求做到从感知到理解，避免将生动活泼的数学思维活动淹没在形式化的海洋里，本文例析对函数概念的理解，在分析和解决问题中培养学生的数学核心素养。

1直接应用概念

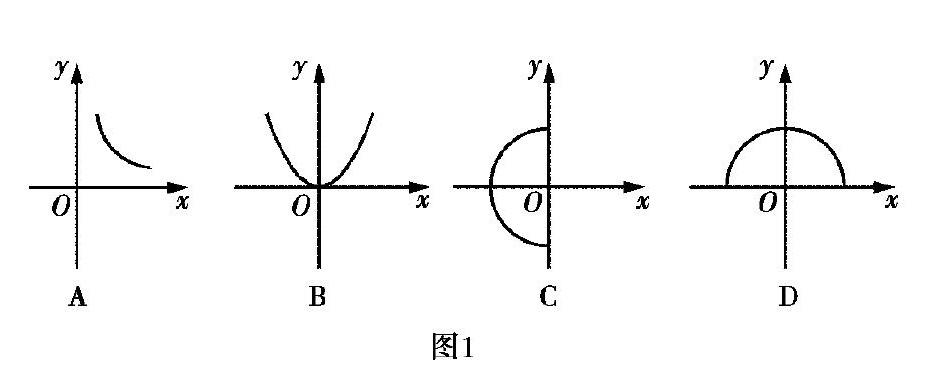
例1下列圖形不能体现y是x的函数关系的是（）。

分析考查了读图能力和函数的定义，根据函数的定义可知：对于x的每一个确定的值，y都有唯一的值与之相对应，将“x的每一个确定的值”转化为图形语言，即作垂直于x轴的直线，左右平移该直线的过程中与函数图象只有一个交点，即y有唯一的值，则该图象是函数图象，否则不是，故选c，

小腾根据学习函数的经验，对线段PC，PD，AD的长度之间的关系进行了探究。

下面是小腾的探究过程，请补充完整：

（1）对于点C在弧AB上的不同位置，画图、测量，得到了线段PC，PD，AD的长度的几组值，见表1：

在Pc，PD，AD的长度这三个量中，确定__的长度是自变量，__的长度和__的长度都是这个自变量的函数;

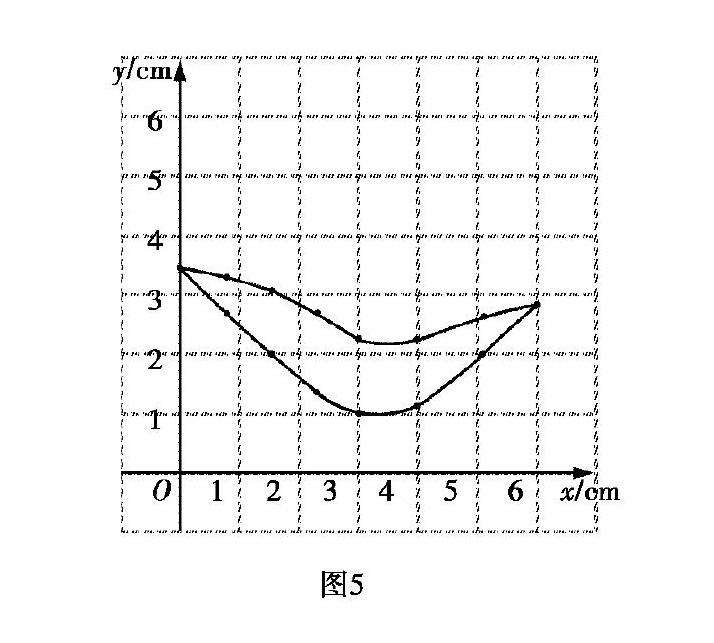
（2）在同一平面直角坐标系xoy中，画出（1）中所确定的函数的图象;

（3）结合函数图象，解决问题：当PC=2PD时，AD的长度约为——cm。

分析本题以函数学习的全过程为背景，考查函数的概念，（1）通过点c在弧AB上的不同位置，画图、测量、列表，分析量与量之间的关系，结合函数定义，容易直观发现，PC，PD的长度随着AD的改变而改变，且当AD的长度确定，PC，PD唯一与之对应，因此，AD的长度是自变量，PC与PD的长度都是这个自变量的函数;（2）描点和画出函数图象，探究变量之间的关系，如图5;（3）利用建立的函数模型解决问题，约为2.29或者3.98.该题通过直观操作活动和多层次的思维活动，引导教学要关注数学活动，更要关注函数的本质。

在概念的教学中，要重视本质教学，即概念的内涵与外延，要让学生经历数学知识的形成、发展和应用，积累数学活动经验，感悟数学思想，培养核心素养，如：体会和理解数学与现实情境的联系，抽象数学问题，建立数学模型;让学生养成画图习惯，充分认识图形带来的好处，重视图形变换，让学生的头脑中留住一些图形，培养空间观念和几何直观，而要真正掌握概念，必须通过应用才能加深理解，现实中蕴含大量与数学有关的问题，通过数学模型，用数学方法予以解决，也体现了数学的应用价值。