降雨环境下的多阶散射蜂窝系统信号特性分析

周 杰，岳 壮

(南京信息工程大学 电子与信息工程学院，江苏 南京 210044)

0 引 言

无线通信系统中，发射机辐射的能量即发射信号在被接收之前可能会通过多种不同的路径传播。无线电波传输所经的路径受多种因素影响，例如：信号传播频率、天线的类型和高度、大气条件和传播地形等。随机分布的散射体(例如树木)会导致发射信号在到达目的地之前产生衰减，散射，衍射和吸收等情况，这种情况就是通信系统中常见的多径效应。多径效应是指电磁波经不同路径传播后，各分量到达接收端的时间不同，按各自相位相互叠加而造成的干扰，这会使原来的信号产生失真，从而影响信号传输质量，造成错误。多径效应对无线通信的影响很大，它不仅是造成信道衰落的一大重要原因，也是限制信道传输带宽和速率的主要原因。对多径效应的研究是无线信道研究的主要工作之一，也是现代通信研究的重要基础。

大量研究的结果表明，植被在无线通信系统的衰落现象中起着重要作用。Tamir[1]作为领域的先驱提出了在森林环境中横波(1-100MHz)传播的概念，研究人员为研究以叶片基质作为传播通道的信道模型付出了很多努力。有学者在尼日利亚翁多州Akure-ilara路线的湿季(树叶茂盛的树木)和旱季(相对去除树叶的树木)分别进行了特高频频段(UHF)广播信号强度衰落效应的测试，并且将获得的结果根据理论估计进行了验证。结果表明，与旱季相比，湿季信号衰减的程度更加严重，并且信号衰减情况是叶片密度的函数。叶片密度越低，接收到的信号越好[2,3]。

除去叶片密度的因素，湿季信号衰减更加严重的一大原因就是降雨造成的多径效应加剧。积累在树叶和枝干上的雨水相当于离散的散射体，会改变电磁波的传播路径，使不同传播波的路径差距更加多样，若路径差为半波长的倍数，则可能导致信号到达时相互抵消从而影响通信质量。然而，由单棵树或大片树林产生的多径效应的影响还没有被深入研究[4]。

1 信道模型简述

几何建模的方法通过通信节点和散射体之间的空间关系的几何抽象来理想化无线信道。几何模型通常以接收信号的到达角(AOA)和到达时间(TOA)统计量的计算为目标。其简单性和较低的计算成本使它们成为无线信道研究领域最为流行的方法。目前已有学者提出了一种基于几何的统计信道模型，其中散射体随机分布在基站周围的圆形区域中，该圆形区域由基站天线的覆盖区域确定。选择瑞利分布和指数分布作为讨论的特例，从而验证了瑞利分布散射体模型可以应用于室外微蜂窝传播环境，而指数分布散射体模型给出了室内办公室/实验室传播环境的精确结果[5,6]，这个结论具有很高的参考价值。基于二维椭圆几何的单次散射信道模型已经被建立，该模型还考虑了树木微小区场景的降雨衰减效应。模型推导了AOA/TOA、边缘TOA和AOA的PDF表达式，从而验证了不同降雨强度对AOA和TOA多径分量的影响[7-9]。然而，降雨情况下无线信号经过多次散射的高阶信道模型仍未被建立。因此，本文通过模拟AOA/TOA PDF联合模型，建立了基于椭圆几何的树木微小区环境二阶散射信道模型，通过与一阶散射模型的对比，进一步分析降雨环境下200 MHZ以上UHF频段的信道空时特性。

图1所示为假设的散射体传播情况，即树木作为散射体均匀分布在假定的椭圆区域中。假设发射机(Tx)和接收机(Rx)分别是基站(BS)和移动台(MS)，位于椭圆区域的焦点位置，Tx和Rx之间的距离D是1000 m,且发射机和接收机处采用的天线均为全向天线。模型中多径信号的信道脉冲响应为

(1)

式中：ai(t,τ)指时间为t，延时为τi(t) 时的信号强度，φ(t,τ) 为相应的相位，δi(t,τi(t)) 则为不同多径分量所对应的单位脉冲强度，N为预设的信号多径个数。考虑降雨强度的不同，传播延迟可以估计为

(2)

式中：参数D为基站到移动台之间的垂直距离，简称为视距，c是无线电波在真空中的传输速度(3e8m/s)，εr为固定值，代表相同电介质层环境下的相对介电常数。

图1 郊区乔木微蜂窝环境模型

如图2所示，本研究将郊区森林环境按水平面高度不同分为4层电介质层环境，即椭圆几何区域中的四层模型。分别假设ε1对应空气冠层，ε2对应冠层，ε3为树干层，ε4对应地面层。由于作为散射体的树木的生物结构特点，树叶大都分布于树干中段树枝繁茂的区域，因此不同高度层面所对应的树叶密度不同，导致不同层面在降雨后叶面积累的雨水量会产生差别，雨水量的不同会导致空气中相对介电常数的变化。因此，不同高度的电介质层可以用来代替不同密度的森林类型，而相对介电常数的变化则可以近似表示降雨强度的不同。假设不同降雨情况下湿冠层的相对介电常数εr介于“稀疏”到“密集”森林类型之间，其所代表的降雨类型为“正常”到“大雨”类型之间。冠层和树干层的垂直高度分别为h1和h2，而空气冠层和地面层之间的高度是无限大的。为简单起见，在本研究中，假设冠层和主干层是介质均匀的，且每一层内都是磁各向同性的，因此不必考虑同一层面的相对介电常数变化，有利于合理的控制变量。

图2 四层环境模型

图3所示为上图椭圆信道的直角坐标模型。模型以基站BS为原点，到移动台MS的垂直距离为D，am和bm为椭圆模型的长半轴和短半轴，根据文献[2]所述

(3)

(4)

式中：参数τm表示传播信号经过散射后的最大延时，该模型适用于天线高度相对较低的微蜂窝环境[10,11]。天线高度较低时，MS可能会接收来自BS附近以及移动设备周围的多径反射[12]。本次研究假设大部分传播信号位于冠层纵向高度，因为冠层中降雨对电磁波平面传播路径的影响最为显著，因此以此模型推导不同情况下的信号传播情况[13]。

图3 椭圆信道坐标模型

2 多阶散射系统的联合概率密度

对于降雨环境下的室外微小区椭圆信道散射系统，对于无线信号的概率密度推算是研究散射信道空间和时间特性的重要参考依据[14]。本文将重点研究椭圆散射系统的二阶散射信道特性，同时与一阶散射信道的仿真结果进行分析对比，从而得出更精准的结论。

2.1 一阶散射信道的联合概率密度

一阶散射系统的2D几何坐标模型如图4所示。该模型展示了传播信号经过散射体单次反射时的传输情况。本研究从信号的单次反射切入，研究其影响和信号传播规律，进而推导信号在多散射体森林环境下的多径传播情况。如图3所示直角坐标模型为基础，为便于推导联合TOA/AOA PDF的最简表达式，本研究以极坐标 (γ,θ) 参数来推导散射体概率密度函数[13]。图中 (rb,θb) 为极坐标系下散射体的实时平面坐标。相关参数在不同坐标系中对应关系为

(5)

(6)

x=rbcos(θb)

(7)

y=rbsin(θb)

(8)

式中： (x，y) 为直角坐标系中散射体的实时坐标，在极坐标系所对应的联合概率密度函数(PDF)为

(9)

其中，J(x,y) 为雅可比变换(Jacobian Transformation)，具体表示为

(10)

代入后可得

frb,θb(rb,θb)=rbfx,y(rbcos(θb),rbsin(θb))

(11)

图4 一阶散射系统几何坐标模型

接着推导rb和多径分量τ的关系。将余弦定律代入图4 极坐标模型，可得

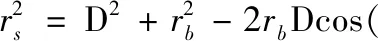
(12)

无线信号路径延迟可化为

(13)

式中：εr为相对介电常数。将公式两端平方化简后求出rb

(14)

可以得到TOA/AOA联合PDF为

(15)

其中，J(rb,θb) 为雅可比变换，具体为

(16)

将式(16)代入式(15)中可得

(17)

将式(11)代入式(17)得出联合概率密度函数为

(18)

式中：rb已由式(14)化简得出，代入后可得基站处散射体联合TOA/AOA PDF表达式为

(19)

由文献可知，散射体均匀分布在任意形状的平面几何区域RA中时[9]，其概率密度函数表达式为

(20)

本研究以此为基础，假设椭圆区域中的树木均匀分布于平面内，因此联合TOA/AOA PDF可表示为

(21)

式(21)得出了基站处的联合AOA/TOA PDF。由于图4中三角几何结构的分布特点，MS处的AOA/TOA PDF与BS处的AOA/TOA PDF具有几何结构上的对称性，因此MS处的联合概率密度函数与BS处形式相同[13]，为

fτ,θs(τ,θs)=

(22)

代入上文中椭圆区域长短半轴am与bm的表达式(3)和式(4)，结合椭圆面积计算公式A=πambm，将其代入式(22)可得联合PDF的最终形式为

(23)

式(23)为降雨衰减作用影响下的一阶散射椭圆信道模型的联合TOA/AOA概率密度函数表达式，θs的物理意义为发射信号到达接收机时的入射角度，εr的变化用于模拟不同环境下的降雨强度。

2.2 二阶散射信道的联合概率密度

frb1,θb(rb1,θb)=rb1fx,y(rb1cos(θb),rb1sin(θb))

(24)

图5 二阶散射系统几何坐标模型

此外，rb1和多径分量τ之间的关系为

(25)

总路径延迟τ可化为

(26)

化简可得rb1为

(27)

由前文可知联合TOA/AOA PDF可表示为

(28)

因此雅可比变换可以化为以下形式

(29)

将式(29)代入式(28)可得概率密度函数

(30)

接下来，用式(27)和式(24)将联合概率密度与原始散射体密度函数相关联，可得

(31)

式(31)表示在基站即发射机处观察到的联合TOA/AOA PDF。根据散射体均匀分布在椭圆形区域内的假设，前文中式(20)已经给出了均匀分布下散射体密度表达式。因此接收机处的概率密度表达式可表示为

(32)

由于椭圆信道模型的焦点对称性，发射机与接收机处的概率密度函数具有相同的形式，因此式(32)即为二阶散射系统联合TOA/AOA概率密度函数的最终形式。

3 仿真结果与分析

本研究利用MATLAB对一阶和二阶系统的联合AOA/TOA PDF进行了仿真。仿真过程中，相对介电常数εr的取值遵循图2所示的4层结构模型，详情见表1。发射机与接收机之间的视距D=1000m，多径信号的到达角θs取值 -180° 到 180°，代表均匀的全向天线。最大延迟分量τm设定为5 μs。根据式(1)的描述，延迟分量τ的取值受εr影响而变化。本研究模拟所假设的多径信号数为50。

表1 相对介电常数εr取值范围

3.1 一阶散射信道特征结果

图6 一阶散射信道PDF分布

图7和图8可以看出，在单一变量的情况下，随着延迟分量τ的增加或信号到达角 (|θs|) 的增大，PDF值逐渐减小,且当延迟分量和到达角度达到最大值时，概率密度最小。由于本实验假设散射体在椭圆区域内均匀分布，同一电介质层介质均匀且磁各向同性，因此AOA与TOA概率分布呈现对称状态。延迟分量固定时，概率密度与AOA的关系呈高斯分布；到达角度固定时，TOA概率密度随时间增加缓慢下降。

一阶信道的仿真结果显示的规律符合参考文献[6]的描述，对于不同的降雨强度，概率密度的分布会有小幅度变化。随着εr的增大，波达信号概率密度的角度分布基本保持不变，但εr的增大会直接导致延迟分量τ的最小值增大，从而使PDF最大值减小，因此仿真结果的Z轴峰值会略微降低。可见降雨作用对一阶散射系统信号到达时间的影响较为明显，而对到达角曲线分布的影响较为轻微。

3.2 二阶散射信道特征结果

图9所示为二阶散射信道的联合概率密度函数分布情况。图10和图11则分别表示单一变量时的信号到达角度与时间的概率分布规律。从图9中可以看出，降雨强度的变化对二阶系统的影响更加明显。当εr=1时，概率密度函数呈现明显的集中分布趋势，即概率密度在θs=0处集中，且数值最大，随着波达信号入射角度增加以及延迟时间的增大，概率密度迅速降低。随着相对介电常数εr的增加，AOA概率密度曲线逐渐平滑，TOA概率密度曲线下降速度也逐渐放缓。

图7 一阶散射信道AOA分布特性

图8 一阶散射信道TOA分布特性

图9 二阶散射信道PDF分布

图10 二阶散射信道AOA分布特性

图11 二阶散射信道TOA分布特性

图10显示了信号到达角在二阶散射信道下的分布规律。与图7所示的一阶环境相比，可以明显看出二次散射后的波达信号到达角更集中分布于0°附近，而随着降雨情况的加剧，达到角分布的密集程度也会有可见的降低。当εr=1时，波达信号的角度几乎集中于0°附近；而εr=1.1时，角度θs开始向0°到50°的区间扩散；当εr达到最大值1.4时，信号到达角的分布区间也增加到100°左右。

图11为二阶散射信道的信号到达时间分布情况。与图8 所示规律相同，降雨程度的加剧会使波达信号的最小到达时间增大，图中可看出随着εr从1增加到1.4，延迟分量τ的最小值从约3.34 μs增加到3.93 μs。而与一阶信道不同的是，信号到达时间的下降曲线随降雨强度的增加而趋向平缓，且相同雨强下曲线的变化幅度更大。

综合上述结果，可知与一阶模型的仿真结果相比，降雨强度的增加同样会加剧波达信号的到达延迟，同时对信号到达角度概率密度分布的影响也更加明显。波达信号在椭圆散射区域中经过散射体的二次散射，其产生的多径衰落现象也会更加明显。从仿真结果可以看出，随着雨强的增加，冠层相对介电常数随湿度条件的增加而增加，这种内部效应使视距与横波到达角呈高斯分布延迟。模拟结果还需进一步分析TOA和AOA的边际密度函数、不同雨强下多径分量的功率延迟分布。

4 结束语

针对降雨影响下的室外环境无线信号传输场景，本文提出了一个基于椭圆几何的郊区森林环境多阶散射信道模型。推导了一阶与二阶散射环境下的无线信号到达角与到达时间的联合概率密度函数，并分析了不同降雨强度下的波达信号角度与时间的概率密度分布规律。仿真结果给出了不同雨强下的TOA/AOA联合PDF分布模型，随着降雨强度的增加，等效的相对介电常数εr增加，这将导致LOS路径分量的到达延迟增大，因此波达信号到达接收机的达到时间将发生延迟，同时联合AOA/TOA PDF的最大值随着εr的增大而减小，且越来越接近均匀分布函数。当无线信号所经历的散射阶数增加，这一现象将表现得更加明显。由于实际信号传输时，传播信号往往会经历多个散射体的多次散射，因此降雨对信号传播的影响将会变得十分显著。本研究为评估平面几何反射信道模型在无线环境中的多径衰落信道参数提供了更为精准的散射体模型，该模型有助于研究LTE通信网络中功率的延迟分布情况，进而推导雨衰情况下的循环前缀，分析OFDM系统性能。