考虑禁飞区的高超声速飞行器再入跟踪控制*

2020-02-07宫梓丰吴玉彬蔡光斌

国防科技大学学报 2020年1期

宫梓丰，刘刚，宋睿，吴玉彬，蔡光斌

(1. 火箭军工程大学核工程学院，陕西西安 710025； 2. 火箭军士官学校测试控制系，山东青州 262500)

近几年来，关于多约束高超声速滑翔飞行器姿态控制问题已成为国内外研究的一个重点[1]。而我国在高超声速滑翔飞行器及其再入技术领域已经取得了迅猛发展，但在试验演习和实战化应用方面仍有一定的差距。滑翔飞行器进入再入阶段后，不仅需要考虑动压、过载、热流密度等约束从而对轨迹进行规划，还必须综合实际打击环境进行避障与突防[2]。最新的制导方法都可以较为完善地应对再入飞行中发生的各类情况，但对于高超声速滑翔飞行器来说，要发挥出其重要的战略突防性能，除却要考虑相关制导方法涵盖的因素，还必须能保证绕过具有地理敏感属性的空域[3]。现今对于禁飞区与飞行器突防的研究仍然相对较浅[4-5]。

通过建立高超声速滑翔飞行器再入段的物理模型，将轨迹优化中的过程约束和终端约束考虑在内，使得整个航程满足禁飞区约束，并尽可能优化控制量是轨迹优化与跟踪控制问题的核心。此问题模型的非线性程度强，且复杂度高，常规的变分法、极大值原理等解析法难以快速求解出最优解，所以一般利用数值法求解轨迹优化与制导控制问题[6]。文献[4]完整介绍了伪谱法作为直接法的典型代表方法，采用了Gauss积分规则的基本原理，而后利用Chebyshev多项式或者Legendre多项式产生配点，最后对系统进行插值处理[7-8]。

采用hp-Radau自适应伪谱法将整个时间区间分区并进行网格细化，同时避免区间中产生过于细密的网格以及难以解算的高次复杂多项式[9]，综合评估网格化密度和插值多项式的幂次，保证系统不仅可以快速收敛，还能够满足既定的精度要求[10]。此种方法可以降低初始条件估计区间误差对结果的影响，将最优控制问题转化为等价的线性规划问题[11-12]。本文经过快速轨迹优化，设计闭环反馈控制器以实现对系统状态的跟踪，通过仿真计算结果计算状态量实时误差，利用积分法设立误差评判标准，评估模型性能得出结论。

1 再入模型构建与控制器设计

1.1 滑翔飞行器再入运动学模型

高超声速滑翔飞行器再入过程中会受到诸多的约束限制，控制系统通道间的耦合现象也较为突出，模型的非线性属性较强，其动态变化可由一组非线性微分方程表征[6，13]。在模型构建中忽略地球的扁率，视其为均匀光滑的球体，可得出滑翔飞行器再入过程中的位置变化方程。

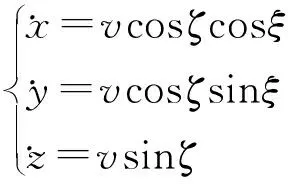
(1)

式中，x、y、z分别为飞行器在再入坐标系下的x、y、z轴向所对应的位置分量，v是飞行器的线速度，ζ为航迹倾角，ξ为航迹偏角。

飞行器的速度、航迹偏角和航迹倾角的一次微分满足：

(2)

式中：Q、S、g、m、φ和σ分别代表飞行器的动压、参考面积、当前位置重力加速度、质量、纬度和倾侧角；KD、KL、KY分别是拟合而成的飞行器阻力系数、升力系数和侧向力系数，其数值一般与飞行器运行的马赫数和攻角相关；Ω=7.292×10-5rad/s，为地球的自转角速度。

飞行器的运动学方程可以表示为：

(3)

式中：α和β是系统的控制量，分别为再入飞行器的攻角与侧滑角；p、q、r分别是再入飞行器的滚转方向角速度、俯仰方向角速度和偏航方向角速度[11]。

飞行器的动力学方程可以表示为：

(4)

式中，b为飞行器的翼展长度，Ixx、Iyy、Izz分别是再入飞行器相对于x、y、z轴向的转动惯量，Kl、Km、Kn分别是通过风洞试验得出的或是拟合而成的滚转、俯仰、偏航乘子系数。

1.2 限制优化问题的约束条件

为使控制问题尽可能切合实际飞行任务要求，在轨迹优化与制导问题中加入禁飞区约束。禁飞区是指飞行器禁止通过的空中区域，比如防空识别区、导弹拦截区等[14]，在优化轨迹的时候必须要绕过禁飞区。

通过分析禁飞区约束的性质[15]，设定禁飞区即路径约束为：

C(x(t),u(t),t)≤0,t∈[t0,tf]

(5)

通常情况下，热流密度、动压和过载被认定是路径约束的一部分，通过不等式组的形式给出[16-17]，其表达式可以按照通用标准定义，也可根据飞行器结构特性来单独定义。对于不同的飞行器外形与材料，以及不同的飞行任务会有不同的约束指标，在此不再赘述。

1.3 优化指标

航迹参数的变化对于规避禁飞区有直接的影响，因而严格控制有关航程参数相对重要。为使滑翔飞行器在再入段获得最大的横向航程，则确定系统的目标函数为：

(6)

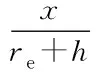
2 问题转化与求解策略

2.1 自适应网格细化方法

数值法求解最优控制问题要先对系统进行时域转换。其中，通过伪谱法求解需要将控制系统的时域映射到[-1,1]，所以先对原时域做相应转换。汲取hp有限元方法的优点，hp自适应伪谱法将时域分成了多个子区间，再将每个子区间上的最优控制问题分别转换为非线性规划(NonLinear Programming, NLP)问题求解[18]。选取K-1个配点,将最优控制问题的整体运行时间即t∈[t0,tf]分成K个子时间区间，将每个子区间的时间定义域[tk,tk+1]转换到区间[-1,1]上，来满足Legendre正交多项式的定义区间[6]。

(7)

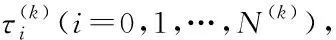
通过这种方法可以将最优控制问题转换为非线性规划问题，可以利用稀疏非线性优化器(Sparse Nonlinear OPTimizer, SNOPT)算法求解此类问题。

设[tk-1,tk]为第k个子区间。取相邻配点之间的中点，以式(8)所示准则来评估误差。

(8)

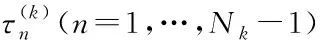
x(k)表示在第k个区间内轨迹的状态。设ρ为判断实施细化标准的标量。若该状态所对应的曲率小于ρ，则认为该区间内的轨迹相对平滑，如果这个区间的精度不满足要求，则可以通过增加区间中的配点数来提升精度，即利用“p法”来提升求解精度；若存在大于ρ的元素，则认定该区间的轨迹不平滑，要通过细化区间网格的方式提升精度，即采用“h法”来提升求解精度。

2.2 反步法求解控制策略

在得出最优轨迹的同时，飞行器再入的全时状态量也可以同步解算，进而得出三通道输出信号，控制副翼、方向舵和升降舵的运行。

式(3)可以表示为：

(9)

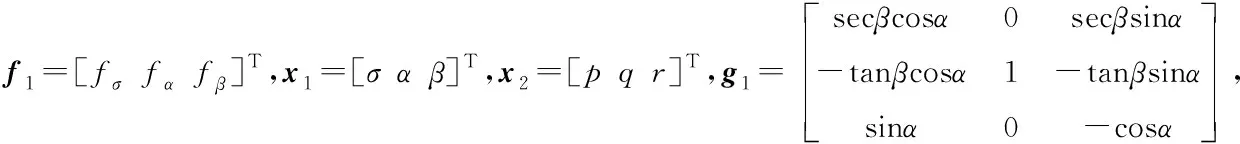
式(4)可以表示为：

(10)

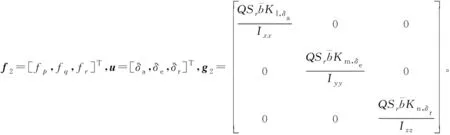
由此可以设计控制回路，构建姿态控制器模型，如图1所示。

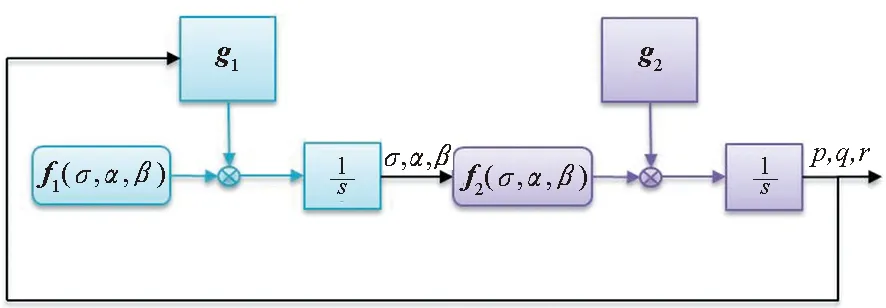
图1 跟踪控制器结构图Fig.1 Structure of tracking control system

下面运用Backstepping的方式设计控制u，实现对前一阶段得出的参考控制量[σd,αd,βd]进行跟踪。Backstepping法又称作反演、反推、反步法，其基本思路是根据系统的阶数，分为若干步骤来实现控制，最终实现对系统目标输出的控制，对于二阶及以上系统的控制优势明显。在分步设计中，需要设计合适的 Lyapunov 函数，设计每一步的虚拟控制函数需要保证Lyapunov 函数一阶导数负定，得到的虚拟控制函数即为下一阶次的控制信号。从控制系统微分方程组的最低阶次开始递归，直到最后一步设计出最终的控制方案。

考虑以下系统，其中g1、g2均可逆。

定义误差变量z1=x1-ξd，ξd为给定的标准状态量，对变量z1求导可得：

(11)

(12)

令x2=z2+x2d，得：

(13)

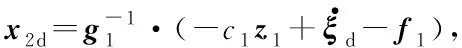
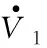
(14)

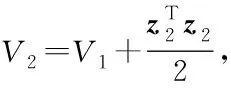
(15)

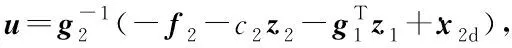
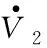
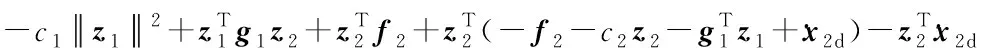
(16)

从式(16)可以看出，选取的Lyapunov函数一阶导数负定，中间变量z1和z2都为有界的，使得变量x1和x2对参考信号[σd,αd,βd]的跟踪误差在可控的范围内，算法实现了对参考信号[σd,αd,βd]的跟踪。

3 仿真试验

3.1 条件与约束

3.1.1 初始条件

飞行器再入的初速度v0=7.8 km/s，再入高度h0=80 km，初始航迹倾角ζ0=0°，初始航迹偏角ξ0=90°。各个方向的初始角速度分量均设为零。

3.1.2 禁飞区约束

根据实际飞行空域识别区限制条件，以飞行器再入点对地面的投影点为原点建立坐标系，设计如式(17)所示的类圆柱形禁飞区域。

(17)

式中，lon代表经度，lat代表纬度，h为高度。

3.1.3 终端约束

vf=800 m/s，hf=25 km，ζf=0°，ξf=90°。

3.1.4 过程约束

在飞行器再入的全过程中，定义法向过载最大值nmax=2.5g，热流率最大值Q=1.2×106W/m2。

3.2 仿真结果与分析

采用上述已知条件，利用hp-Radau自适应伪谱法对再入飞行问题进行解算，仿真实验在MATLAB2018a软件中运行，设定配点精度为1×10-6。

通过轨迹优化，可以得出高超声速飞行器运行的最优轨迹，进而得出最优轨迹高度变化曲线，如图2所示。

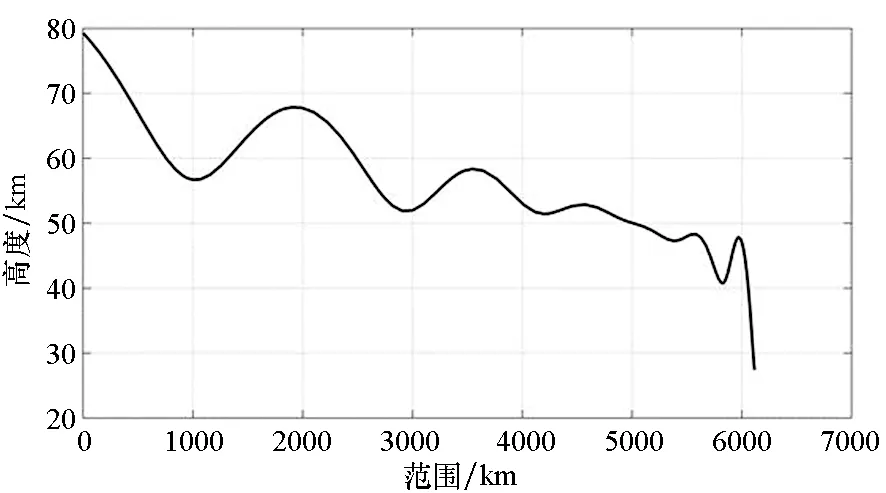
图2 再入高度曲线Fig.2 Reentry height curve

飞行轨迹呈跳跃式，相较于平滑下降的“钱学森”弹道，其能耗更小，可以增加飞行航程。不仅如此，飞行器在稠密与稀薄的大气层交替穿行，可以减少滑行过程中的热能损耗，使得最优控制问题中的热能约束更容易被满足，最优解的选择更宽泛。整个飞行过程中，飞行器速度下降过程偏于平稳，除此之外，遵循这种飞行方案可以保证其热流密度不会出现间歇尖峰，有利于保护飞行器的本体结构不被损坏。

最优轨迹的控制量(攻角)变化如图3所示。

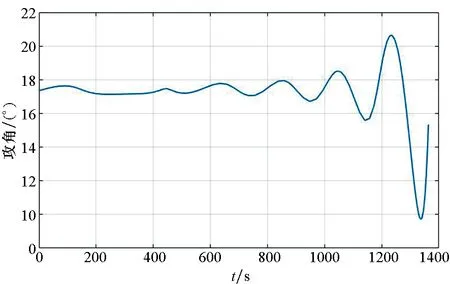
图3 攻角变化曲线Fig.3 Curve of AOA

使用倾斜转弯(Bank To Turn， BTT)飞行控制模式，即在航迹坐标系中，设定攻角与侧滑角为控制量，全程攻角控制在25°以内，使得三通道控制信号耦合程度尽量轻微，从而容易有效实现系统控制。

加入禁飞区约束后，其飞行轨迹将要做出必要调整，原始轨迹与优化后的飞行轨迹如图4、图5所示。

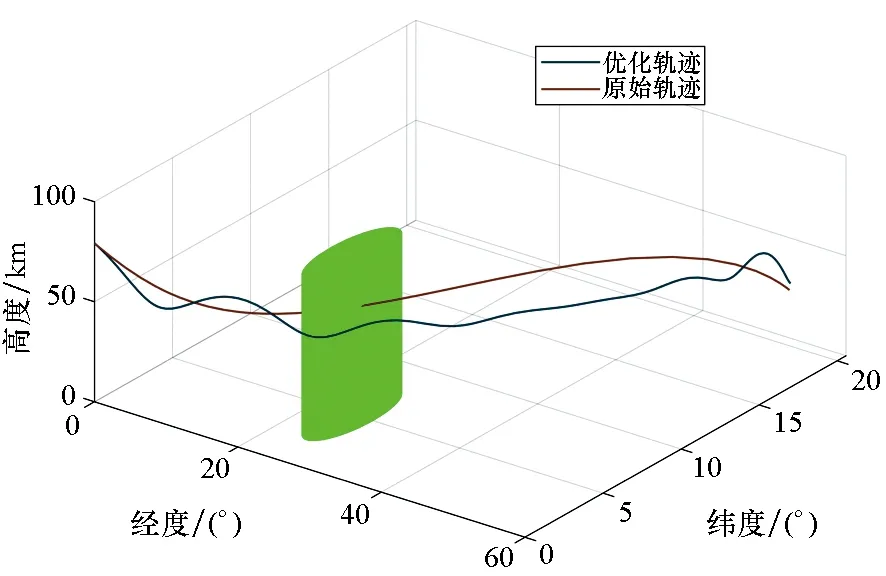
图4 优化前后轨迹立体图Fig.4 Trajectory stereogram before and after optimization

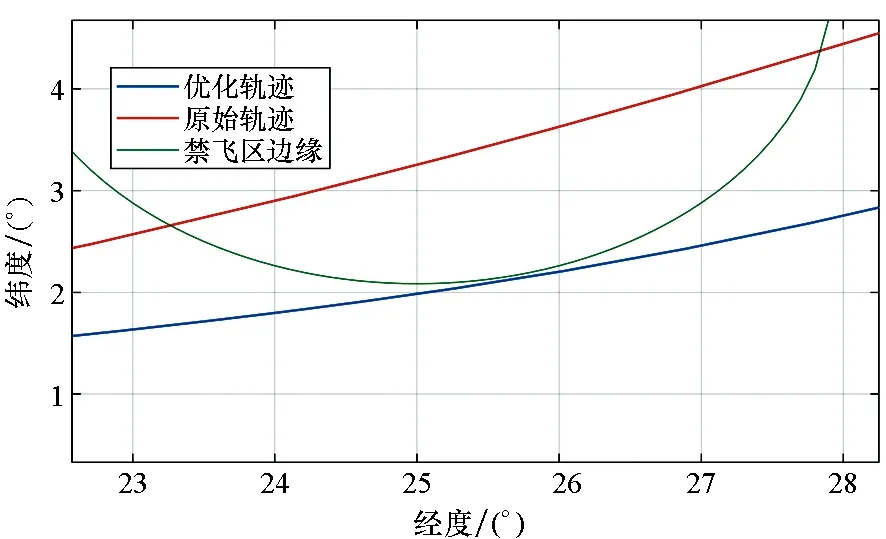
图5 优化前后轨迹局部平面图Fig.5 Trajectory partial layout before and after optimization

由图4和图5可知，飞行器沿着优化轨迹飞行即可避开禁飞区，达成优化指标的同时完成突防任务。

根据状态量与控制量的动态关系，可以得出滚转、俯仰、偏航三通道的角速度，进而导出副翼、方向舵和升降舵的控制信号，如图6所示。

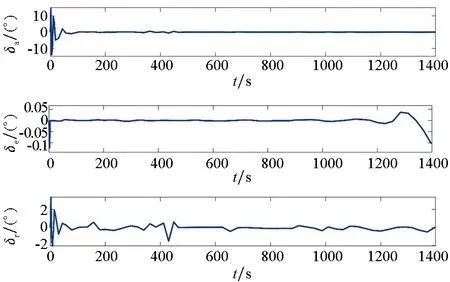
图6 副翼、方向舵和升降舵的控制信号Fig.6 Control signals of aileron, rudder and elevator

以此控制信号对三自由度角速度进行跟踪，跟踪情况如图7～9所示。

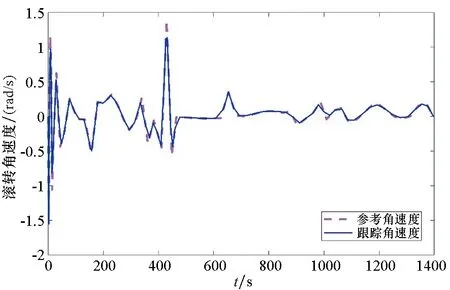
图7 滚转角速度的跟踪情况Fig.7 Tracking of rolling angular velocity

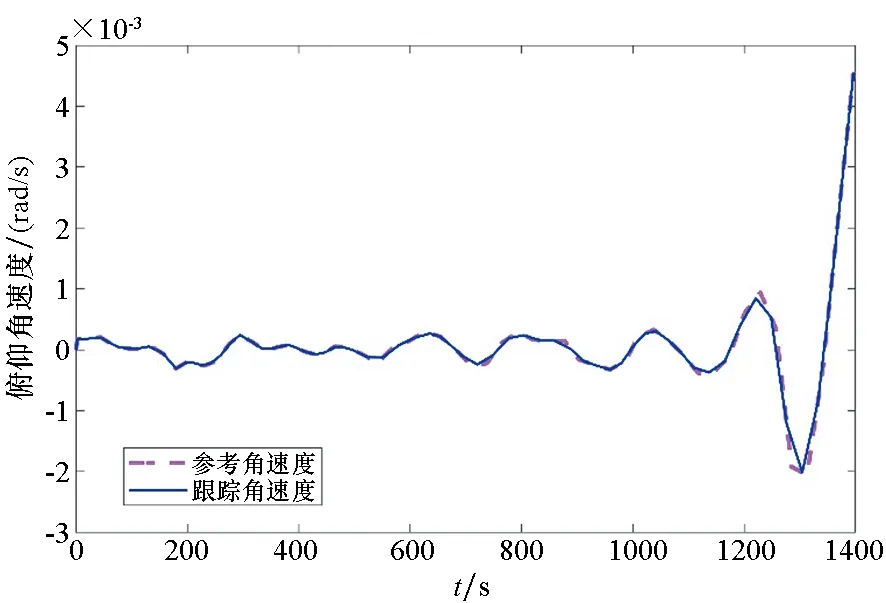
图8 俯仰角速度的跟踪情况Fig.8 Tracking of pitch angular velocity

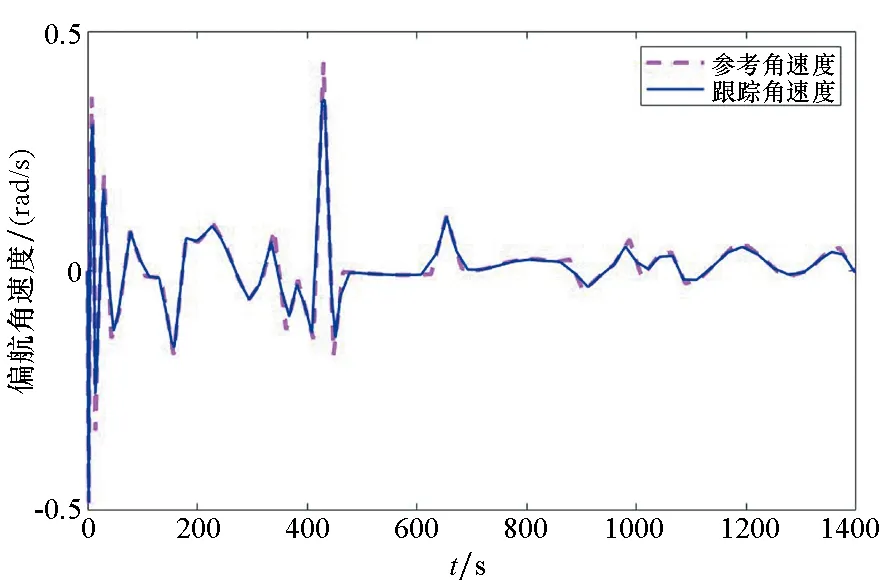
图9 偏航角速度的跟踪情况Fig.9 Tracking of yaw angular velocity

由图7～9可知，系统对三个自由度的角速度变量能够有效实现实时跟踪，系统设立的采样时间间隔约为40 s，由控制信号控制得到的角速度误差因素主要来自目标采样和控制信号时间传导。

对攻角和倾侧角的跟踪效果如图10、图11所示。

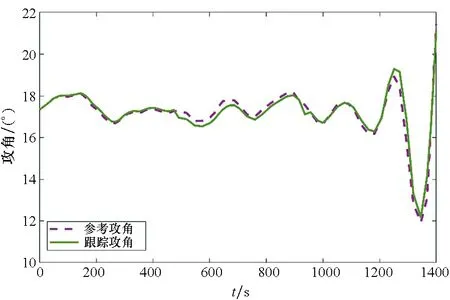
图10 攻角的跟踪情况Fig.10 Tracking of angle of attack

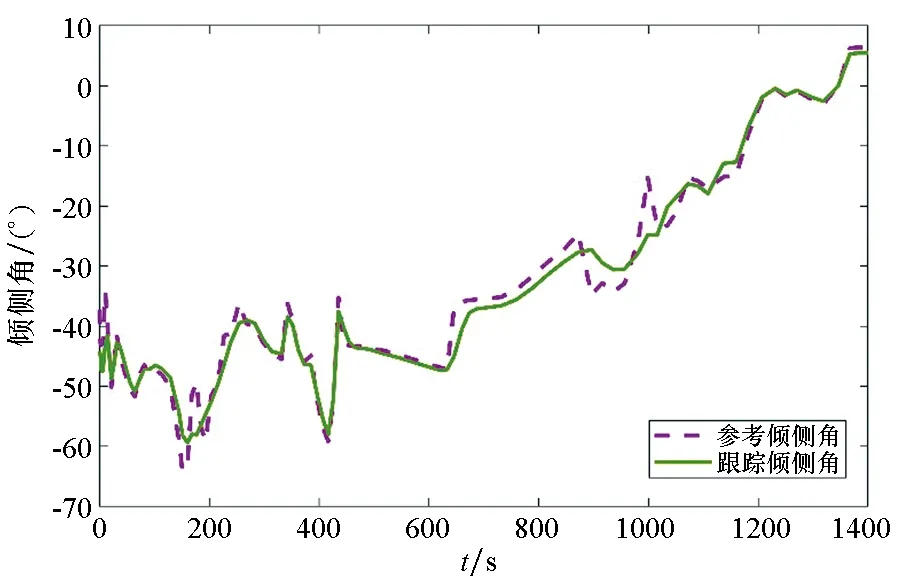
图11 倾侧角的跟踪情况Fig.11 Tracking of bank angle

由图10、图11可以看出，跟踪控制器已经实现对于系统控制变量的实时跟踪。在系统存在干扰的情况下，依然可以完成正常输出，保证高超声速飞行器再入的姿态稳定。跟踪信号的攻角变化较小，因而与之对应的俯仰角速度会相对较小，由于采样时刻俯仰角速度的突变量较小，所以系统对攻角的跟踪效果较好；而倾侧角与滚转角速度和偏航角速度有关，由于偏航角速度和滚转角速度存在较多的瞬时振荡，尤其是在飞行器再入初始阶段和飞行轨迹策略重新优化的阶段，因而跟踪侧滑角难度相对较大。由于每个采样点间存在一定时间间隔，系统对其跟踪效果会有一定误差，但此误差最终依然可以收敛。系统仿真验证了控制模型能够达到预期输出，可以有效跟踪高超声速飞行器再入时的控制变量，进而实现机动快速调姿。