高焓CO2气流壁面两步催化机制对非平衡气动加热影响的数值模拟*

2020-02-07杨肖峰桂业伟杜雁霞肖光明

国防科技大学学报 2020年1期

杨肖峰，桂业伟，邱波，杜雁霞，肖光明

(1. 国防科技大学空天科学学院，湖南长沙 410073；2. 中国空气动力研究与发展中心空气动力学国家重点实验室，四川绵阳 621000)

火星进入器经历长时间深空航行后，以极高速度进入火星大气层，在高效进入减速过程中，产生复杂且特殊的气动热环境[1]。长时深空飞行和特殊进入环境均给火星进入飞行带来很大的不确定性[2]，进而给进入器热防护系统设计和评估带来挑战[3]，而防热结构重量尽量轻、性能足够可靠的轻量化设计需求对火星进入器高超声速气动加热精准的预测提出了更加苛刻的要求[4]。然而，与地球再入环境不同[5]，以CO2及其离解产物高超声速流动为主要特征的火星进入非平衡效应突出[6]，进入器壁面催化效应以碳氧粒子吸附和结合为典型特征，这对防热大底表面物理化学行为和气动加热水平有显著的影响，进而给火星进入器热防护系统选材和防热性能评估带来了新的挑战[7]。

由于火星进入任务的飞行数据稀缺，且在地面模拟进入火星大气环境的试验技术难度大、成本高，因此，结合少量地面热考核试验，开展大规模计算模拟成为解决上述问题和挑战的主要研究思路[8]。为此，有大量学者针对高焓CO2气流环境下的壁面催化效应开展了物理机制、理论建模和数值模拟研究。

针对高焓离解CO2流动环境，Bykova等[9]基于高频等离子体发生器开展了多种材料/涂层的表面催化效率测定。Kolesnikov等[10]通过试验测试和数值计算建立了中高温段材料催化效率关联式(最大在10-2量级)，并初步获得了亚声速离解CO2流动作用下的典型材料催化特征。针对碳氧离解环境壁面催化效应的物理建模问题，Bose等[11]基于CO2离解混合物，建立了考虑CO2和O2复合反应的单步催化模型，并参数化地获得了催化路径对壁面热流的作用规律，研究表明CO2复合反应对热流有主导性影响。上述单步机制难以有效表征高焓气体在壁面的微观行为，为此，Mitcheltree等[12]基于CO2复合反应机制，建立了组分表面吸附、气态组分与吸附组分结合等两步反应模型，获得吸附、结合速率受控的壁面催化效应。Afonina等[13]进一步考虑O2的复合反应，建立了更复杂的两步催化模型，通过离解CO2环境下催化路径若干权重比对，发现材料催化表征因素繁杂且对加热特性影响显著，但该研究未给出催化路径与加热特性的定量关联。上述催化建模研究表明，壁面催化模型以及材料催化路径、效率等参数对防热材料壁面气动加热有显著的影响[14]，但尚未回答何种催化路径占主导以及催化参数的强弱对气动加热的影响规律等问题。

尽管已存在基于现象学和表面化学的壁面催化模型，但是防热材料及其涂层的催化性能和可能的催化路径各异，测试和表征方法也存在差异性[15]，因此火星进入催化加热特性的有效预测尚存在问题。面对材料催化特性的表征和预测问题，尤其针对火星进入高焓碳氧离解环境，如何剥离同时发生的O2和CO2结合反应进而分析催化反应路径的比重和离解物的消耗权重，如何建立壁面粒子吸/解附与结合的制衡关系并定量关联催化性能/路径与非平衡加热水平，亟须利用数值模拟手段开展进一步的研究。

1 计算方法

1.1 化学反应流动求解器

高超声速化学反应流动求解器以考虑有限速率化学反应的三维层流可压缩Navier-Stokes方程组为基本控制方程，其守恒形式[16]为

(1)

其中，Q为守恒型状态变量向量，F、G和H为三方向的无黏(对流)通量向量，Fv、Gv和Hv为黏性(扩散)通量向量，S为化学反应源项。假设高超声速化学反应流动是化学非平衡而热力学平衡的。界面或壁面上热流通量由热传导(温度梯度)项和组分扩散(质量分数梯度)项两部分组成

(2)

其中，T为温度，κ为导热系数，n为法向坐标，Ns为组分个数，hs为组分s的绝对焓(显焓+化学生成焓)，Js为组分s的扩散质量通量。

使用具有总变差减小(Total Variation Diminishing, TVD)性质的有限体积法对控制方程进行数值离散。在空间方向上，无黏通量使用二阶van-Leer方法作矢通量分裂，黏性通量采用中心格式离散，界面通量采用带有van Albada限制器的MUSCL方法插值求得。在时间方向上，采用LU-SGS隐式方法作时间推进。对化学反应源项，采用流动/反应解耦算法，保持原有隐式方法优势的同时可有效解决化学反应生成率[17-18]。

针对高焓离解CO2气体混合物，采用基于Park化学动力学的5组分 (C, O, O2, CO和CO2) 6化学反应(r1～r6)气体模型[19]，化学反应方程式和第三体组分如表1所示。化学反应涉及的速率常数见文献[20]。

表1 高焓离解CO2气体混合物化学反应机制

高焓CO2离解气体混合物各组分的热力学特性考虑分子平动能、转动能、振动能和束缚电子激发能[21]。各组分的黏性系数由Blottner拟合关系式获得。关于能量和质量的输运特性，热传导系数由普朗特数给出，取Pr=0.71；等效扩散系数由施米特数给出，取Sc=0.5。多组分混合气体的热力学和输运系数由Wilke公式计算获得。

1.2 壁面热化学模型

考虑壁面催化效应的复杂壁面热化学模型满足壁面动量、质量和能量平衡关系[19]。具体地，动量平衡需满足常规零压力梯度条件，质量平衡需满足各组分的质量守恒方程

(3)

其中，cs为组分s的质量分数，ρ为气体密度，Ds为等效扩散系数。壁面催化效应造成相关组分在壁面产生一定量值的质量通量，而壁面总通量为零。能量平衡需满足壁面对流换热、辐射散热等能量传递形式总和为零，即

(4)

其中，Tw为壁面温度，ε为辐射发射率，σ为斯提芬玻尔兹曼常数，qw，c为温度梯度所致热流量。组分s的扩散质量通量Js由壁面与组分s有关的有限速率催化反应机理来获得。

对壁面多化学反应系统，组分s的摩尔通量Is由相关反应路径c的摩尔通量Ic所确定，即

(5)

其中，Nc为总反应路径数，Nrc和Npc分别是反应路径c的反应物和生成物个数，δij为Kronecker函数。

假设壁面反应是不可逆的，反应路径c的摩尔通量Ic受控于壁面化学反应速率常数和反应物浓度，即

(6)

其中，kc为化学反应速率常数，Nr为反应物个数，ν为相应组分的化学当量数，X为有关反应物的物质的量浓度。

1.3 CO2复合的两步催化机制

高焓CO2气体的离解组分混合物在固体壁面上发生特定形式的复合反应。这里采用壁面吸附、Eley-Rideal结合、解附及近壁扩散等多步反应机制对该过程进行物理建模[15]。这些反应尽管涉及气固界面气体组分和吸附位分子/原子的微观运动，但在宏观层面可用速率系数来表征，涉及的吸附、Eley-Rideal结合等速率系数由材料实验测定或更小尺度理论模拟来获取[22]。

基于CO2离解产物及其化学结合特点，建立壁面吸附和Eley-Rideal结合速率受控的两步催化模型 (假设解附速率无限大，忽略解附对壁面反应的影响)，该模型考虑O和CO两种粒子吸附进程、O2(s)和CO2(s)两个Eley-Rideal结合进程、CO+O(s)和O+CO(s)两个CO2(s)结合路径，具体的催化机制如表2所示。涉及的壁面催化反应均为放热过程，其中O2复合反应过程生成焓498 MJ/kmol，CO2复合反应过程生成焓528 MJ/kmol。涉及的速率常数在所关注范围内由参数化给出，尽管催化强度难以确定，但参数化数据和关联规律可为催化特性研究提供理论支撑。

表2 CO2离解气体混合物壁面两步催化反应机制

吸附和Eley-Rideal结合的反应速率常数k依赖于防热材料的分子平均热速度vm、催化效率或吸附系数γ、活化能E等热化学特性参数[22]，具体表达为

(7)

其中：R0= 8314 J/(kmol·K)为通用气体常数；Φ为材料表面吸附位总浓度；vm与壁面温度Tw相关，由分子平均热动能求得

(8)

基于壁面反应物浓度和热化学特性参数计算壁面反应速率，获得壁面质量通量和化学反应吸/放热量，进而建立CO2复合的两步催化机制。

2 计算模型与算例验证

2.1 几何模型与计算网格

本文数值研究所采用的几何模型为70°球锥布局，该布局为美国历次成功着陆火星表面的进入器防热大底的典型布局，布局示意如图1所示。Marschall等[22]针对该布局的缩比模型在LENS-I反射激波风洞[23]中进行了高焓气动加热实验，模型最大截面直径76 mm，实验以CO2为测试气体。本文以1/4区域为对象，基于该实验的测试数据开展数值计算研究。

图1还给出了流体域内的计算网格。网格为多块六面体结构网格，壁面法向足够正交且适当加密。网格无关性研究表明，壁面法向第一层网格高度雷诺数为Rec= O(1)，可保证壁面热流计算值具有较高的预测精度。

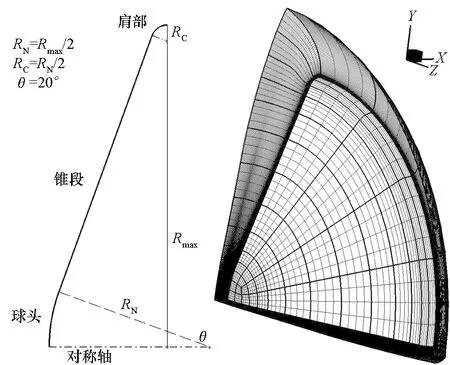
图1 70°球锥布局示意及相应的计算网格Fig.1 70° sphere-cone configuration and computational grid for hypersonic flow

2.2 算例验证

所使用的可压缩流动求解器已经过大量计算流体力学(Computational Fluid Dynamics, CFD)计算验证，具有精确有效的气动加热预测能力[16, 19, 24-25]。在此基础上，基于MacLean等[23]的高焓气动加热实验，进一步验证所发展的壁面催化模型的有效性。

表3给出了数值计算所需的自由来流条件，该来流条件将产生较高程度的高焓离解CO2气流。数值计算涉及三种壁面条件，即完全非催化(Non-Catalytic, NC)、完全催化(Fully Catalytic, FC)和有限速率催化(Finite-Rate, FR)。关于有限速率催化壁，假设催化活化能Ec为零，进而忽略了吸附和催化反应的能量壁垒；假设实际吸附位活性体浓度足够大，进而忽略了表面吸附位对壁面反应速率的限制。据此假设，壁面催化反应速率仅与特定反应的催化效率γc这一关键因素有关。

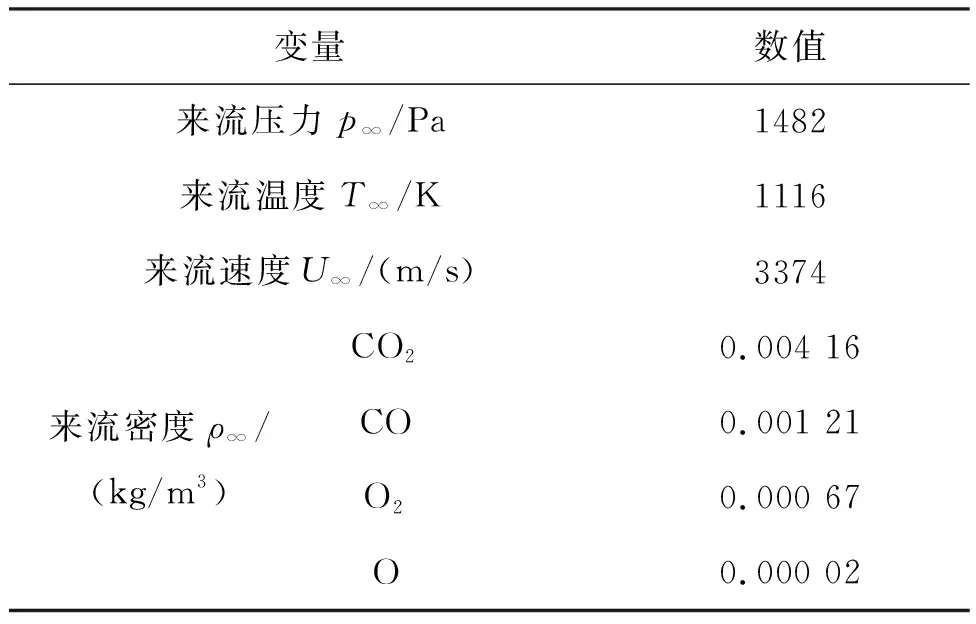
表3 高焓CO2气流数值计算的自由来流条件

基于不同催化模型计算获得的高超声速无黏流场相近，催化效应的影响范围仅限于边界层流动的近壁区域。通过数值计算，图2给出了高焓CO2气流作用下对称面位置的温度等值线图，可见温度场分布合理，激波形状和脱体距离符合预期，流场结构正确可信。

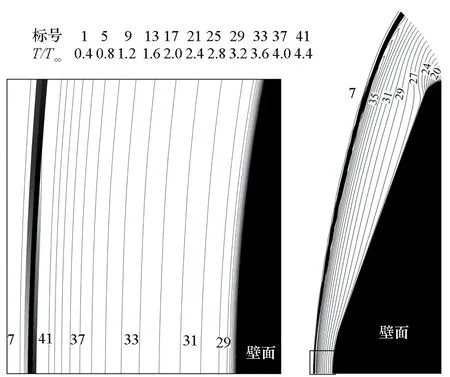
图2 高焓CO2气流作用下对称面上的温度等值线图Fig.2 Temperature contour in high-enthalpy CO2 flow on the symmetry plane

图3给出了NC和FC条件下的壁面热流分布计算值(Calc)以及与文献[23]中DPLR软件计算值(Ref)的对比结果。可以看出，壁面热流分布规律符合预期，两种催化条件下的计算值与DPLR值在除肩部大曲率部位外的大部分区域吻合度良好。通常的壁面催化加热实验难以达到完全非催化或完全催化条件，即实验状态的催化加热是有限速率的。图4进一步将计算结果与风洞实验数据[23](Exp)作对比，可见，NC计算结果整体上低于实验值，而FC计算结果整体上高于实验值，这与有限速率催化加热的物理规律相一致。

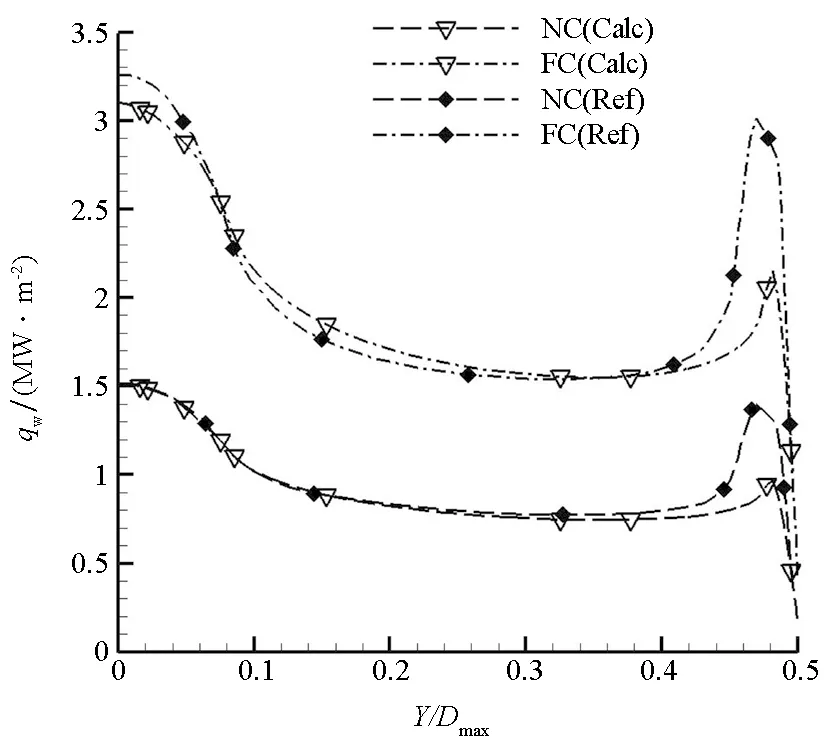
图3 完全非催化和完全催化条件下壁面热流计算值与文献计算值的对比结果Fig.3 Comparison of heat fluxes from computation and reference on the fully and non-catalytic walls

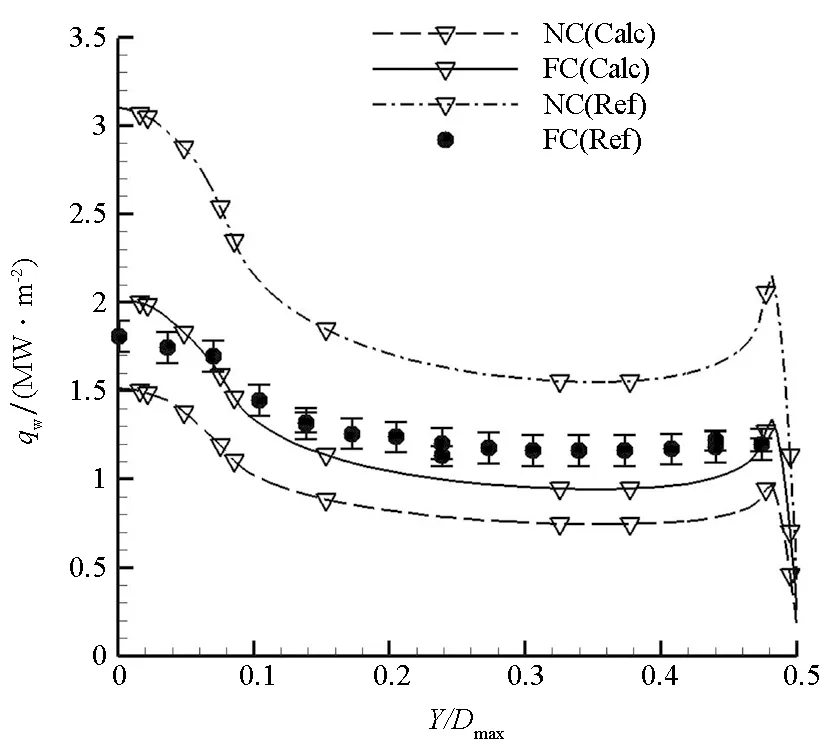
图4 有限速率催化条件下壁面热流计算值与实验值的对比结果Fig.4 Comparison of heat fluxes from computation and experimental data on the finite-rate catalytic wall

基于所建有限速率壁面催化模型，考虑O2和CO2的复合反应，给定各吸附反应的黏附系数为1且各催化反应的催化效率为1，开展相同条件下的有限速率催化加热数值模拟，结果如图4所示。在该条件下，计算获得的热流值介于NC和FC壁之间，理论上符合预期；计算值在驻点略高于实验值，而在大面积区域略低于实验值。尽管实验条件下的催化反应系数难以确定，但是相比于催化效应的上下极限，有限速率催化得到的热流值更接近于实验值。算例验证表明，所发展的模型在处理非平衡有限速率壁面催化加热方面具有一定的适用性。

3 结果与讨论

火星进入流动特有的高焓碳氧环境，存在多种壁面催化机制，且受壁面化学反应和近壁面扩散的共同作用。因作用速率不匹配性，存在多种依赖关系，对壁面法向各组分质量通量和热流通量有直接影响。为了弄清壁面高温催化效应对非平衡气动加热的影响规律，开展壁面材料催化效率及不同催化复合路径对非平衡气动加热影响的参数化数值模拟研究。

3.1 材料催化效率对气动加热的影响

为考察防热材料的催化特性对非平衡气动加热的影响规律，根据表2所建立的催化反应机制，开展相同来流(见表3)条件下的非平衡气动加热数值模拟和参数化研究。数值模拟单独考虑各自的Eley-Rideal结合过程并考虑上述结合过程的组合情况，有关的壁面黏附系数和催化效率的参数化见表4，其中C1仅考虑吸附反应Ad1和结合反应ER1的化学反应进程(Ad1+ER1)，其他吸附/结合速率为零；C2仅考虑Ad1+ER2进程；C3仅考虑Ad2+ER3进程；C0考虑所有的上述进程。

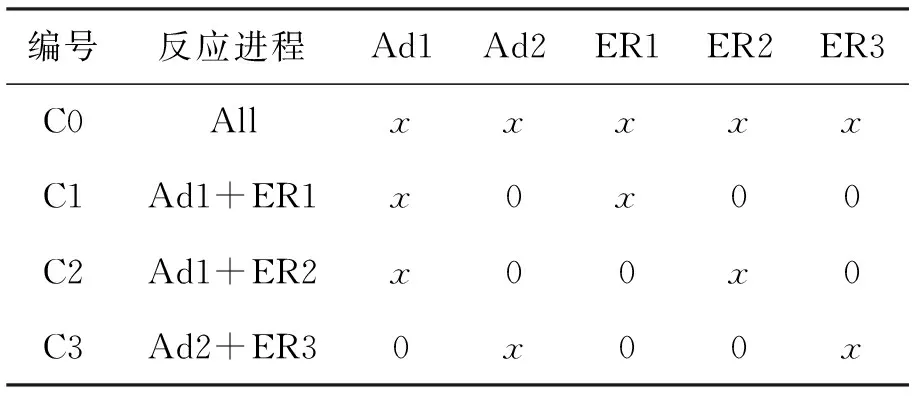
表4 壁面各化学反应黏附系数和催化效率参数

注：x为可变参数，在数值模拟中同步改变。

图5给出了不同催化路径条件下驻点热流随催化效率的变化曲线。整体上，催化效率越高，壁面化学反应越剧烈，反应产热越多，驻点热流随催化效率的增高而增加。图6进一步给出了不同催化条件下中心线上的质量分数分布曲线。根据高焓碳氧环境离解特性，激波层内O含量明显低于CO含量。因C1过程(见表4)只消耗气相中有限的O，CO未参与复合反应，故复合放热作用较弱，驻点热流值相对较低。C2和C3过程(见表4)同时消耗气相中的CO和O，故复合放热作用较强，进而驻点热流值相对较高，且C2和C3得到的气动加热值基本相同。图5中各条曲线的曲率显示，催化加热量随催化效率的增大而单调增加，且对中等催化材料 (10-3<γ<10-2)具有较高敏感度。

在3个催化反应过程中，ER1和ER2共同消耗吸附位生成物O(s)，ER1和ER3共同消耗气相组分O，而ER2和ER3所消耗的吸附位组分与气相组分互换，且具有相同的生成物。壁面CO2两类结合反应和O2结合反应并存，且存在相互竞争关系，使得进入器防热材料在高焓碳氧离解气流作用下表现出更复杂的催化特性。

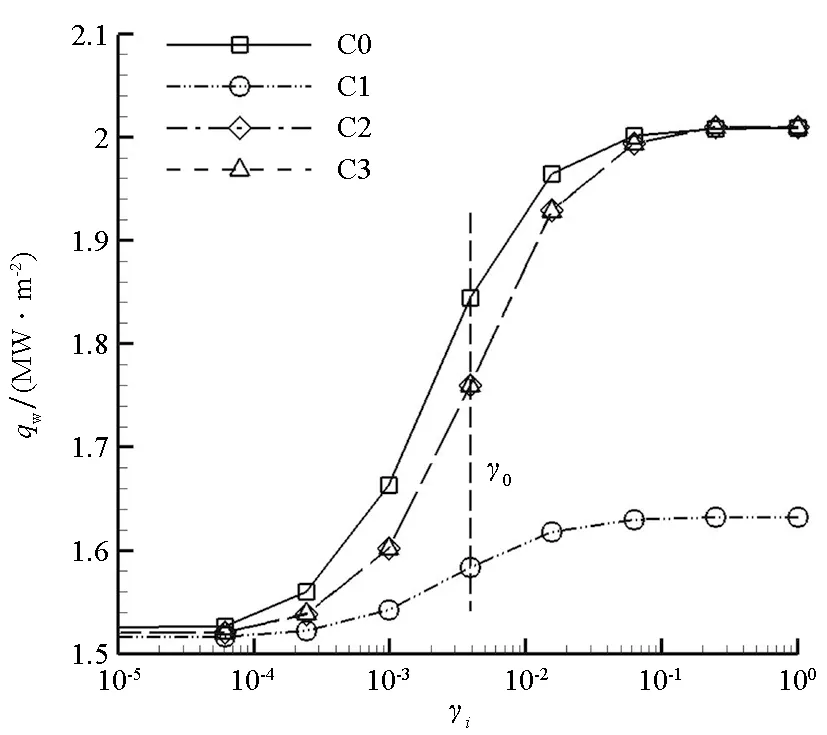
图5 驻点热流随黏附系数/催化效率的变化曲线Fig.5 Stagnation heat flux curves with sticking coefficient/catalytic efficiency

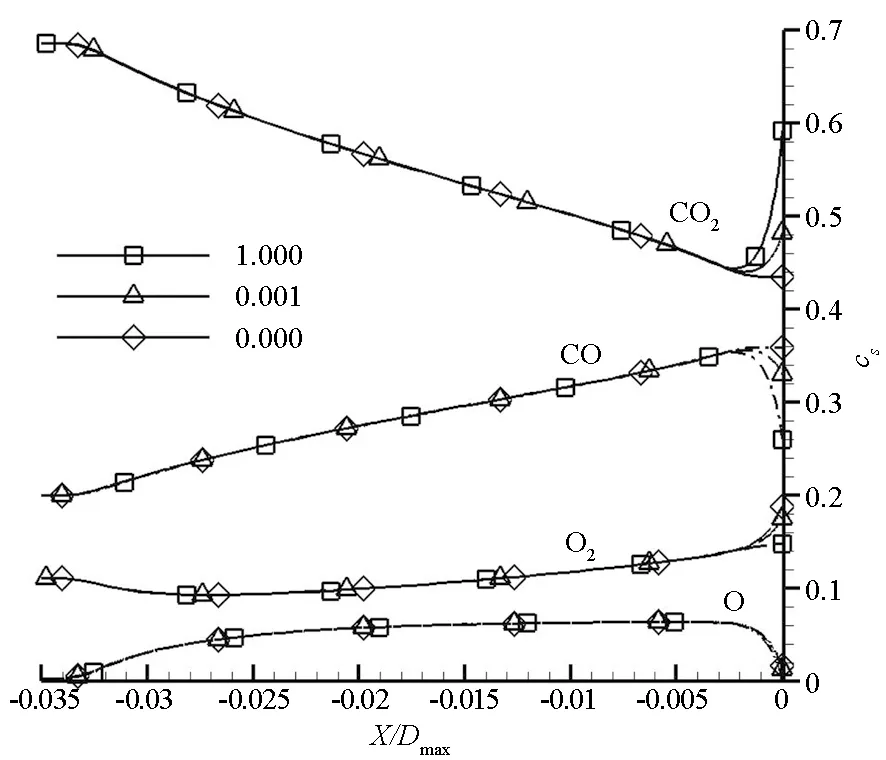
图6 不同催化效率条件下中心线上的质量分数分布曲线Fig.6 Mass fraction curves on the centerline with various catalytic efficiency

计算发现，同时考虑ER1、ER2和ER3三个催化反应进程获得的驻点热流值高于单个催化进程结果，即在特定的组合催化条件下可获得相对更高的气动加热量。研究结果进一步说明了材料催化路径对壁面热流有一定的影响，而催化复合路径对气动加热水平的影响规律直接影响材料遴选和结构设计，为此尚需要做进一步的研究。

3.2 催化复合路径对气动加热的影响

为了研究防热材料的催化复合路径对气动加热水平的影响规律，研究两个催化路径a和b(ER1和ER2、ER2和ER3或者ER1和ER3)存在一定耦合作用下的非平衡催化加热特性。在总催化效率γa+γb=γ0的情况下，分别计算不同组合权重ωab=γa/(γa+γb)条件下的化学非平衡气动加热，计算条件见表5。这里取γ0=2-8，一方面在该条件下壁面热流对催化特性的敏感度最显著，另一方面经实验测定火星进入器所采用的防热材料多以中等催化为主[9-10]。

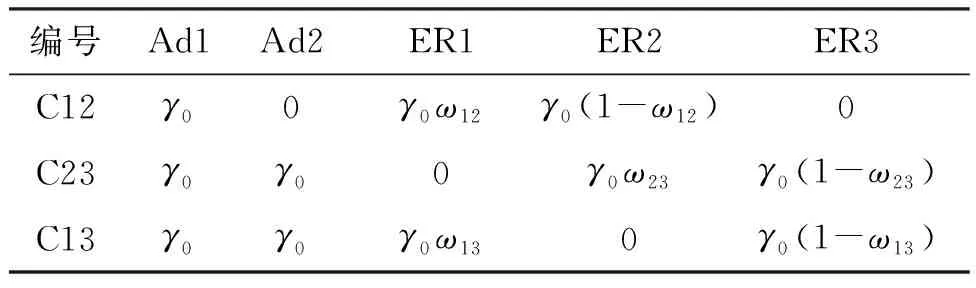
表5 壁面组合反应黏附系数/催化效率参数

注：ω为可变参数，在数值模拟中同步改变。

图7分别给出了三类组合催化作用下驻点热流随组合权重的变化曲线。关于ER1和ER2组合(表5中C12)，随着组合系数ω12的增大，ER1参与反应的比重增高，ER2相应降低，CO参与壁面反应的通量降低，驻点气动加热水平单调下降。ER1和ER3组合(表5中C13)情况同理。

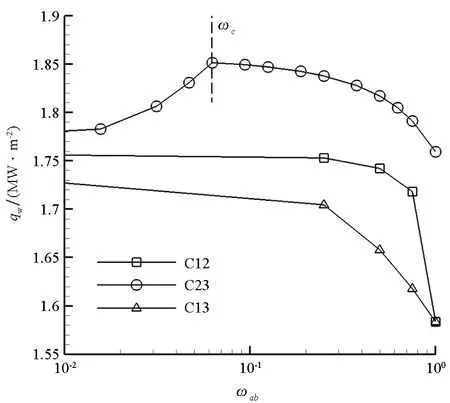
图7 驻点热流随组合权重的变化曲线Fig.7 Stagnation heat flux curves with weighting factors

关于ER2和ER3组合(表5中C23)，随着组合系数ω23的增大，ER2参与反应的比重增高，ER3相应降低，但计算结果显示，驻点气动加热值与组合权重不存在单调关系，而在ω23=ωc附近出现热流峰值 (在该计算条件下ωc≈0.062 5)。也就是说，考虑CO2存在的CO+O(s)和O+CO(s)等两条复合路径的联合作用，得到的壁面热流要大于单个作用的热流结果。

为了理解ER2和ER3在特定组合条件下气动加热高于单个作用的现象，考察不同组合权重条件下的吸附反应(Ad1和Ad2)、Eley-Rideal结合反应(ER2和ER3)及其综合作用过程(Ad1+ER2和Ad2+ER3)的驻点摩尔通量。

关于Ad1+ER2反应进程，图8给出了驻点Ad1和ER2的理论摩尔通量和该进程(Ad1+ER2)实际摩尔通量随组合权重的变化曲线。由于近壁面气相O有限(见图6)，Ad1的理论摩尔通量处于较低的水平；而由于近壁面气相CO充足(见图6)，ER2的理论摩尔通量随组合权重的增大而逐渐增加。催化作用进程的驻点综合摩尔通量受吸附反应摩尔通量和理论Eley-Rideal结合反应摩尔通量的共同限制。因而，Ad1+ER2综合摩尔通量在ω23<ωc区段受限于低水平的ER2，在ω23>ωc区段受限于速率有限的Ad1。在二者共同限制下，Ad1+ER2综合摩尔通量随组合权重的增大而缓慢增大。

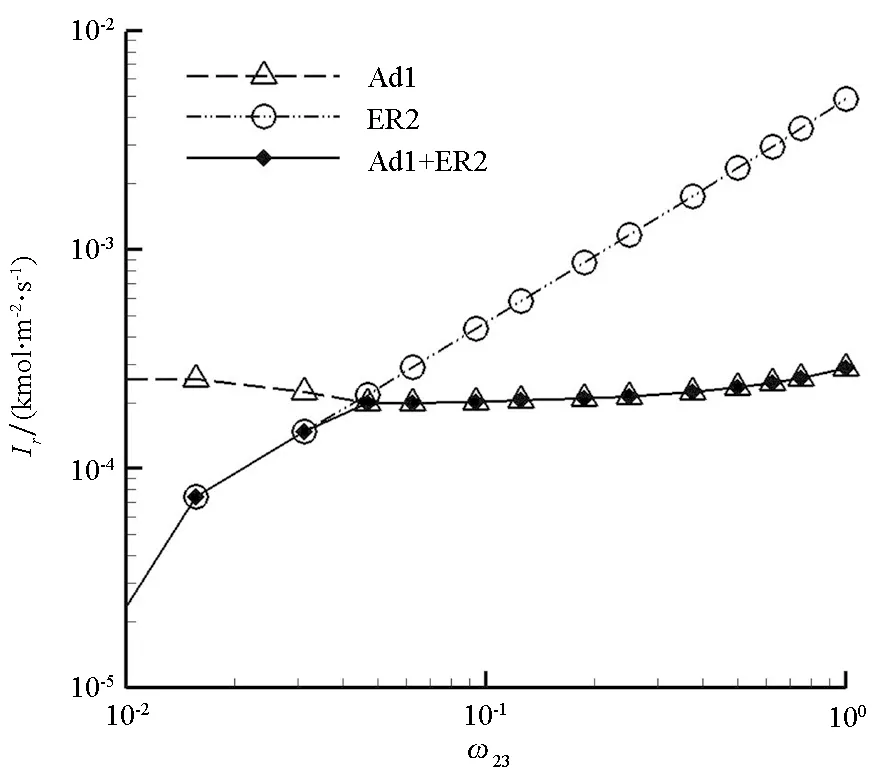
图8 Ad1和ER2理论摩尔通量和Ad1+ER2综合摩尔通量随组合权重的变化曲线Fig.8 Theoretical mole fluxes of Ad1 and ER2, and integrated mole flux of Ad1+ER2 with weighting factors

关于Ad2+ER3反应进程，图9给出了驻点Ad2和ER3的理论摩尔通量和该进程(Ad2+ER3)实际摩尔通量随组合权重的变化曲线。由于近壁面气相CO充足(见图6)，Ad2的理论摩尔通量保持较高的水平；而由于近壁面气相O有限(见图6)，ER3的理论摩尔通量随组合权重的增大而逐渐减小。Ad2+ER3综合摩尔通量因Ad2过快(CO过量)而在整个组合区段均受限于ER3反应速率，综合摩尔通量随组合系数的增大而减小。

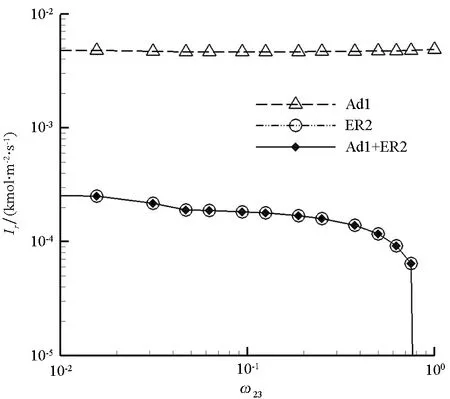
图9 Ad2和ER3理论摩尔通量和Ad2+ER3综合摩尔通量随组合权重的变化曲线Fig.9 Theoretical mole fluxes of Ad2 and ER3, and integrated mole flux of Ad2+ER3 with weighting factors

图10进一步给出了驻点ER2和ER3的实际摩尔通量及总通量随组合权重的变化曲线。二者之和先增后减，并在ω23=ωc附近出现摩尔通量峰值，进而造成在当前权重条件下气动加热水平高于两个极端情况(ω23=0或ω23=1)。

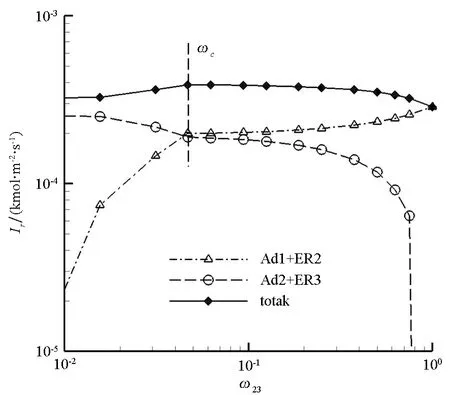
图10 各进程综合摩尔通量及总摩尔通量随组合权重的变化曲线Fig.10 Integrated mole fluxes of each reaction pathway and total mole flux with weighting factors

在本算例中，CO的浓度大于O的浓度，O相对有限(见图6)，峰值所处组合权重出现在更靠近有利于Ad2+ER3反应进程的位置。改变流场碳氧元素的质量分数，图11给出了驻点热流随组合权重的变化曲线对比图。可以看出，当近壁O组分比重较高时，峰值所处的组合权重位置ωc更靠近1，即在相同条件下壁面催化机制更趋于Ad1+ER2反应进程。由此可知，气动加热峰值所处的组合权重位置ωc与近壁面气相CO和O的浓度有关。根据高焓碳氧气体混合物的离解特性[25]可知，在进入速度较高时，因CO2离解度较高，O含量较高，CO2催化由Ad1+ER2反应进程主导；反之，在进入速度较低时，CO2催化由Ad2+ER3反应进程主导。因此，进入器在高超声速进入火星大气层飞行过程中，防热大底表面先后出现Ad1+ER2反应进程主导转向Ad2+ER3反应进程主导的CO2催化加热机制。

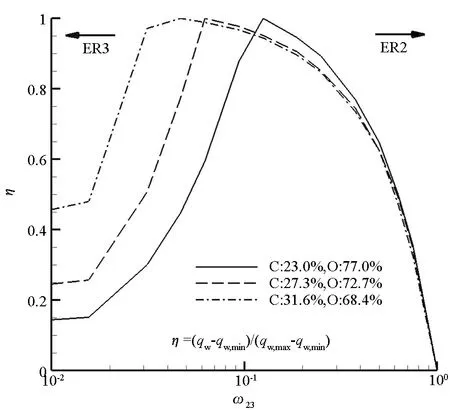
图11 不同组分条件下驻点热流随组合权重的变化曲线Fig.11 Stagnation heat flux curves with weighting factors for various species fractions

数值研究获得了CO2两步催化路径权重与加热量之间的非单调关联关系，研究表明特定权重下两种路径联合作用的热流高于单个催化结果，热流峰值所处权重与近壁相关组分浓度相关。考虑催化路径权重与加热量之间的上述非单调关联关系，进一步研究特定结合路径条件下的材料催化特性，深入研发催化复合路径可控的新型防热材料，可为轻量化、低冗余的热防护系统设计提供理论基础，也给材料的评价和设计带来了新的挑战。