高原环境对弹丸动态稳定性的影响*

马国梁，张海洋，蔡红明，常思江

(1. 南京理工大学 能源与动力工程学院， 江苏 南京 210094；2. 中国兵器工业导航与控制技术研究所， 北京 100089； 3. 南京理工大学 机械工程学院， 江苏 南京 210094)

弹丸的气动外形通常表现出轴对称特点，而弹丸的动态稳定性问题一直是外弹道学的基本问题之一[1]。著名外弹道学者Murphy早年建立了一套完整的弹丸运动稳定性理论[2]，采用复攻角方程来描述弹丸的角运动特性，这一方法被国内外的外弹道学书籍广泛采用[3-4]。国内研究人员一直对弹丸飞行稳定性的相关问题进行积极探索。王良明针对细长弹丸表现出的气动弹性进行了稳定性研究[5]，闫晓勇等研究了火箭弹章动运动的稳定性条件[6]，王华毕等研究了无控低速滚转火箭弹的锥形稳定性问题[7]。随着常规弹丸灵巧化、制导化技术的发展，一些新型弹药的运动稳定性问题也得到了国内外学者的重视。杨永亮等研究了末敏子弹的稳态扫描条件[8]，刘俊辉等利用滑模理论分析了脉冲修正弹制导回路的稳定性[1，9]。Wang等分析了控制策略对固定鸭舵双旋弹的稳定性影响[10]，周伟采用拟线性方法研究了有控旋转弹锥形运动稳定性[11]。

不同海拔高度对弹丸弹道特性存在很大影响，我国的云贵高原、青藏高原等地区海拔高度较高，为了保障国家安全，就对火炮武器提出了高原地区的使用需求。王良明等对平原环境和高原环境下的弹丸飞行稳定性差异进行了分析[12]，主要针对高炮发射的旋转稳定弹。钱明伟分析了高原气象条件和高原空气动力特性对弹道参数的影响，研究了高原射表的编制方法[13]。刘志明等指出马格努斯效应是影响卷弧翼火箭弹高原飞行失稳的主要原因[14]。由于空气密度低是高原环境的重要特点，钟扬威等以空气密度作为分岔参数，计算分析了弹箭角运动的分岔特性[15]。

本文用现代控制理论的状态空间方法来分析弹丸动态稳定性，建立了弹丸角运动的四阶状态空间模型，通过符号化求解得到两对共轭复根，利用复数平方根计算方法得到特征根实部的表达式。鉴于陀螺稳定因子和动态稳定因子的传统定义，提出了弹丸稳定因子的新定义，稳定因子不仅能够分析弹丸是否动态稳定，而且能够定量刻画动态稳定性的强弱。分析表明，基于稳定因子定义的新的动态稳定条件与传统外弹道学的动态稳定条件完全一致。讨论了低空气密度对旋转稳定弹和尾翼稳定弹动态稳定性的不同影响。研究结果表明，高原环境对于尾翼稳定弹的动态稳定性会产生不利影响。

1 动力学建模

1.1 坐标系定义

1.1.1 地面发射坐标系

地面发射坐标系与地球表面固连，坐标原点定义在炮口断面中心，x轴沿水平线指向射击方向，y轴在水平面内，垂直射击面向右(由弹底部前视)，z轴按右手法则定义指向下方。为简化研究，将地面发射坐标系近似为惯性坐标系。

1.1.2 地面发射坐标系

弹道坐标系坐标原点O位于全弹质心。xp轴沿飞行速度方向，yp轴沿水平方向，zp轴按右手法则定义。由地面发射坐标系按右手旋转方法依次转过弹道偏角χ和弹道倾角γ可以得到弹道坐标系，转换矩阵为：

(1)

1.1.3 非滚转弹体坐标系

非滚转弹体坐标系顾名思义不随弹体滚转，坐标原点O位于全弹质心，xb轴与弹体纵轴重合指向弹头，yb轴指向右侧，zb轴按右手法则定义。非滚转弹体坐标系由弹道坐标系按右手旋转方法依次转过侧滑角β和攻角α得到， 转换矩阵为：

(2)

1.2 弹体气动力及气动力矩

1.2.1 阻力

弹体阻力大小为0.5ρV2SCD，阻力与飞行速度方向相反，S为参考面积，V为飞行速度，CD为阻力系数。

1.2.2 升力

按照外弹道学的习惯[1]，升力在弹道坐标系中的向量表示为：

(3)

式中，CLα为弹体升力系数。

1.2.3 马格努斯力

马格努斯力在弹道坐标系中的向量表示为：

(4)

式中：p为弹丸转速；d为参考长度，这里取弹的直径为参考长度。

1.2.4 俯仰力矩

俯仰力矩在外弹道学专业中习惯称为静力矩或者翻转力矩，弹体坐标系中的俯仰力矩向量为：

(5)

式中，CMα为弹体俯仰力矩系数。

1.2.5 俯仰阻尼力矩

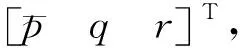
(6)

式中，CMq为俯仰阻尼力矩系数。

1.2.6 滚转阻尼力矩

滚转阻尼力矩在外弹道学道中习惯称为极阻尼力矩，滚转阻尼力矩大小为：

(7)

方向指向弹体纵轴，Clp为滚转阻尼力矩系数。

1.2.7 滚转力矩

装有斜置尾翼的弹丸或者涡轮火箭弹都存在滚转力矩，滚转力矩大小为：

(8)

方向指向弹体纵轴，Cl为滚转力矩系数。

1.2.8 马格努斯力矩

非滚转弹体坐标系中马格努斯力矩向量为：

(9)

1.3 线性化方程

根据牛顿第二定律，在弹道坐标系中写出弹丸的力方程组如下:

(10)

(11)

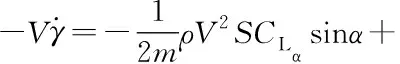
(12)

根据动量矩定理，可得弹丸的力矩方程组如下：

(13)

(14)

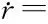
(15)

其中，Ix为轴向转动惯量，Iy为横向转动惯量。根据角速度的坐标转换关系可以得到如下方程：

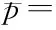
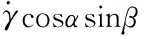
(16)

(17)

(18)

(19)

其中，

根据传统弹丸的气动参数大小和物理几何参数的特性，忽略影响较小的量，有：

(20)

2 动态稳定性分析

2.1 坐标系定义

根据线性系统稳定性理论可知，如果状态矩阵A的所有特征根具有负实部，则弹丸是动态稳定的。通过符号化求解，可得A的四个特征根为：

(21)

(22)

(23)

(24)

其中，a=4M+H2-P2，b=2P(2T-H)，i为虚数单位。

根据复数的平方根计算方法[16]，可以进一步对特征根的形式进行整理，b≥0时，四个特征根可以表示为如下两对共轭复根：

(25)

(26)

b<0时，四个特征根可以表示为如下两对共轭复根：

(27)

(28)

共轭复根的虚部取值不同，实际上对应了传统外弹道学中角运动的快圆和慢圆动态特性。两对共轭复根的实部取值也不同，分别为：

(29)

(30)

(31)

若式(31)成立，则满足λs<0，系统所有特征根的实部为负。外弹道学传统上习惯采用陀螺稳定因子与动态稳定因子的经典约束条件来判别动态稳定性，这里统一采用稳定因子λs来分析动态稳定性，在应用上更简单直观。在λs<0的前提下，|λs|越大，飞行攻角向平衡点的收敛速度越快，动态稳定性越好，这也为定量分析动态稳定性提供了方便。

动态稳定条件式(31)成立的必要条件是H>0，根据弹丸气动系数的特点可知升力系数CLα>0，俯仰阻尼力矩系数CMq<0，自然满足H>0。

2.2 与传统动态稳定条件的一致性

进一步检查动态稳定条件式(31)与传统的动态稳定条件是否一致。将a、b的表达式代入式(31)，由于H>0，整理可得式(31)的等价条件为：

(H2-P2+4M)2+4P2(H-2T)2-(H2+P2+4M)2<0

(32)

进一步化简为：

P2T2+H2M-HP2T<0

(33)

情况1：对于转速为0的弹丸，式(33)等价为M<0，这意味着只要弹丸是静稳定的，就一定是动态稳定的，比如某些单兵武器发射的弹丸，转速接近于0，就属于这种情况。

情况2：对于具有转速的尾翼稳定弹，比如某些尾翼稳定火箭弹，式(33)两边除以P2H2，整理可得式(33)的等价条件为：

(34)

沿用外弹道学动态稳定因子的定义为：

(35)

将式(35)代入式(34)可得：

(36)

当0≤Sd≤2时，不等式(36)右边Sd(2-Sd)≥0，只要弹丸是静稳定的，即M<0，弹丸一定是动态稳定的，当Sd<0或者Sd>2时，动态稳定条件变为：

(37)

这种情况下，转速不能过大，否则会导致动态不稳定。

情况3：对于旋转稳定的弹丸，沿用陀螺稳定因子定义：

(38)

将其代入式(36)可得：

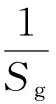
(39)

根据二次函数的性质，无论动态因子Sd如何取值，函数Sd(2-Sd)的最大值为1，因此对于旋转稳定弹，陀螺稳定因子Sg>1是动态稳定条件成立的必要条件，当Sg<1时，动态稳定条件不成立，稳定因子λs>0，弹丸将是动态不稳定的。

由以上讨论可知，新的动态稳定条件式(31)与传统外弹道学的动态稳定条件是一致的。

3 低空气密度对动态稳定性的影响

3.1 尾翼稳定弹

对于转速为0的尾翼稳定弹,由稳定因子的定义及式(31)～(33)的分析推导过程可知，若|H2M|越小，|λs|动态稳定性越弱，按照式(20)展开H2M，有：

(40)

可以看出，|H2M|随着密度的减小而减小，在其他弹道参数都一致的情况下，高原低密度条件下的|λs|在数值上小于平原条件下的|λs|，也就是说，转速为0的尾翼稳定弹在高原环境的动态稳定性相对平原地区而言变差。因此对于这一类弹丸如果想在高原环境下使用，需要加大静稳定性，从而保证高原环境的动态稳定性，比如可以采用增大尾翼面积的做法。

(41)

根据轴对称弹的气动特性可知，CLα>0，CMq<0，弹丸在超音速飞行状态时，通常CMpα>0，而弹丸在亚音速小攻角的飞行状态时，马格努斯力矩系数的极性会发生改变，会出现CMpα<0的情形，进一步导致Sd<0。以尾翼稳定的火箭弹为例，通常为了消除不对称性使火箭弹丸具有一定转速，大射角条件下弹道顶点附近更容易出现低亚音速的情形，也就更容易出现马格努斯力矩系数极性变化的问题。在高原空气密度较低的条件下，静稳定力矩减小到一定程度导致弹丸飞行时无法克服马格努斯力矩系数为负的影响，就会导致平衡点动态不稳定，飞行攻角增大；而马格努斯力矩系数随着攻角增大又变为正值，就容易出现极限环的情形。一些理论和试验表明，这种情况下，弹丸的角运动状态由一个动态不稳定的平衡点趋于一个稳定极限环，弹丸呈现一种锥摆运动的状态，攻角较大的极限环会导致飞行阻力明显增加，就出现所谓的“近弹”和“掉弹”问题，难以达到正常的射程要求。

3.2 旋转稳定弹

对于旋转稳定弹M>0，由陀螺稳定因子Sg的定义可知，高原环境下密度减小时，Sg增大，更容易满足动态稳定条件式(39)，也就是说，旋转稳定弹只要在平原大气环境下是动态稳定的，在高原大气环境下更能满足动态稳定性，这一点与文献[12]的研究结论是一致的。

4 仿真计算分析

4.1 算例分析

某型号尾翼稳定弹具有一定转速，弹丸物理几何参数和气动参数如下：d=0.122 m，S=0.011 7 m2，CLα=2.01，CD=0.24，CNpα=-0.16，CMpα=-3.2，Cl=0.9，Clp=0.024 8，CMq=-12，m=13.6 kg，Ix=0.023 4 kg·m2，Iy=0.231 87 kg·m2。

弹丸初速为205 m/s，初始转速为15 r/s。在平原0 m海拔高度发射时，按炮兵标准气象条件取空气密度ρ=1.206 3 kg/m3，根据式(29)计算稳定因子λs=-0.1<0，表明弹丸是动态稳定的。如果在高原5000 m海拔高度发射时，空气密度ρ=0.73 kg/m3，稳定因子λs=0.033 3>0，角运动状态方程将出现正实部特征根，弹丸在高原发射条件下将是动态不稳定的。

4.2 弹道仿真

采用文献[1]中120 mm口径、转速为0的尾翼稳定迫弹数据进行外弹道仿真。外弹道仿真初始条件为：弹丸初速318 m/s，射角45°，其他初始条件为0。采用标准炮兵气象条件，分别在海拔0 m的平原条件和海拔4500 m的高原条件下进行外弹道仿真计算。全弹道的稳定因子变化曲线如图1所示。

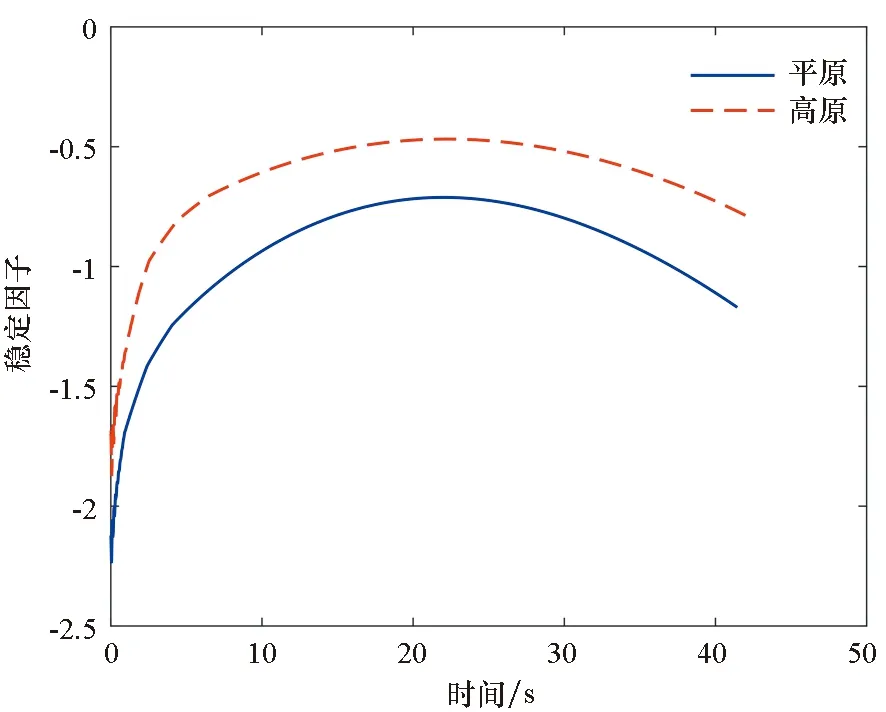
图1 稳定因子变化曲线(射角45°)Fig.1 Curves of stability factor (Quadrant elevation 45°)

对弹道高度进行仿真计算后得知，高原和平原条件下都在飞行时间接近21 s处到达弹道顶点。由图1可以看出，弹丸稳定因子的绝对值在弹道顶点处最小，意味着弹道顶点处弹丸动态稳定性最弱，而且高原条件下弹丸稳定因子绝对值偏小，意味着该型号迫弹在高原使用时相对平原的动态稳定性降低。

其他初始条件不变，射角改为65°，仍分别在海拔0 m的平原条件和海拔4500 m的高原条件下进行外弹道仿真计算。按照式(29)计算稳定因子λs，全弹道的稳定因子λs变化曲线如图2所示。

图2 稳定因子变化曲线(射角65°)Fig.2 Curves of stability factor (Quadrant elevation 65°)

图2的仿真结果同样说明该型号迫弹在高原使用时相对平原的动态稳定性降低。比较图1和图2还可以看出，弹道顶点处的稳定因子绝对值在65°射角条件下取值更小，意味着较大射角条件下弹丸的动态稳定性更弱。

5 结论

在经典的弹丸动态稳定性理论基础上，采用状态空间模型研究得出了新的基于稳定因子的动态稳定条件。稳定因子为负表明弹丸是动态稳定的，而且稳定因子绝对值越大动态稳定性越强。基于新的动态稳定条件对弹丸在平原和高原的动态稳定性差异进行了分析，结果表明：

1) 对于转速为0的尾翼稳定弹，如果弹丸是静稳定的就一定是动态稳定的，在高原使用时该类弹丸的动态稳定性降低，而且在其他弹道参数一致的条件下，较大射角条件下弹丸动态稳定性较弱；

2)对于具有一定转速的尾翼稳定弹，如果动态稳定因子满足0≤Sd≤2，那么静稳定的弹丸在平原和高原都能保证弹丸的动态稳定性，而平原和高原稳定因子的强弱差异取决于弹丸的具体参数。

3)对于具有一定转速的尾翼稳定弹，如果弹丸动态稳定因子Sd<0或者Sd>2，弹丸在高原使用时就可能出现动态不稳定的情况。比较常见的情形是，马格努斯力矩系数为负值导致Sd<0，高原使用时由于空气密度的下降导致静稳定力矩减小，最终不能满足动态稳定条件。

4)旋转稳定弹如果在平原使用时满足动态稳定条件，那么在高原使用时更容易满足动态稳定条件。

相关试验表明，一些具有相当转速的尾翼稳定火箭弹在平原使用时飞行稳定，但在高原使用时出现明显问题。高原条件下这类火箭弹在小攻角时动态不稳定而在大攻角时动态稳定，表现为锥摆运动，最终由于较大攻角导致阻力显著增加，出现“近弹”现象，使得高原射程远小于正常的平原射程，这一现象的产生机理及稳定性分析仍需做进一步的研究工作。考虑到工程的实际需要，本文采用线性化分析方法讨论了角运动状态方程的局部稳定性，在后续的研究中将尝试采用非线性系统稳定性分析方法讨论全局动力学特性。