基于不完全测量数据的飞行器轨迹参数估计*
2020-02-07李冬,刘学
李 冬,刘 学
(中国人民解放军91550部队, 辽宁 大连 116023)
在航天测控领域,通常利用光学、雷达等多个测量设备对飞行器跟踪测量,再由采集到的测量数据给出飞行器高精度的轨迹参数估计。在此跟踪测量过程中经常出现不完全测量的情况,即测量设备由于工作状态不理想或受到环境干扰,在某些时段丢失大量测量数据,导致无法解算完整的轨迹参数,直接影响了后续的精度评估工作。如何利用不完全测量数据获得精度尽量高的轨迹参数是测控数据处理亟须解决的难题。
飞行器轨迹参数估计通常采用基于样条函数表示的数据融合方法[1-3],在不完全测量情况下,该方法的估计模型呈现病态性,难以有效确定轨迹参数。文献[4]利用误差诊断方法,在完全测量段落获取辅助测量设备低精度测元的系统误差,扣除系统误差后融合其他设备少量的高精度测元用于估计不完全测量段落的轨迹参数,获得较高精度的估计结果,但该方法的前提是具有辅助测量设备并且该设备的测元完好,在实际应用中受到限制。文献[5]利用飞行器轨迹的动力特性优化轨迹的表示样条,在丢失部分测量数据的情况下,仍然能够获得较高精度的轨迹参数,但是该方法只适用于不完全测量段落较短的情况,当丢失数据的时间较长时,估计模型依然呈现病态性,估计结果并不理想。不完全测量问题本质上是病态逆问题,信号处理领域的稀疏优化方法被大量应用于病态逆问题的研究[6-9],该方法充分利用先验知识进行信号优化建模,得到信号的稀疏表示,通过确定少量参数即可实现真实信号的重构,从而缩小参数空间维数,将病态问题转变为良态问题。值得注意的是,信号稀疏优化问题求解困难的根源在于信号的稀疏结构或支撑未知,很多方法的出发点都是要解决这一问题。而对于飞行器来说,其轨迹参数的稀疏结构在一定程度上是可建模的,可用样条模型表示[2-3,10]。国内外一些学者将稀疏优化方法应用于样条拟合问题的研究中。文献[11]通过求解l1范数稀疏优化问题使拟合样条的待求参数最小化,提高了拟合性能。文献[12]建立了多分辨率样条基函数集合,采用稀疏优化方法从集合中挑选出少量基函数,用其表示函数曲线能够有效减少待求参数的数量。文献[13]由插值样条函数的l0范数稀疏优化获得函数曲线的稀疏表示。
本文针对不完全测量条件下的飞行器轨迹参数估计问题,提出了一种基于稀疏优化的轨迹参数估计新方法。该方法将轨迹参数用B样条函数表示,结合不完全测量数据建立轨迹参数估计的稀疏表示寻优模型,通过样条节点的稀疏优化最大限度压缩样条节点数,从而降低参数空间的维数,缓解模型的病态性。
1 飞行器轨迹参数的稀疏表示寻优模型
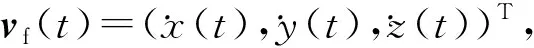
(1)
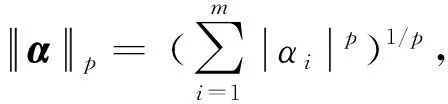
(2)
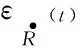
y(t)=f(x(t))+ε(t)
其中,f(x(t))为测量真值,ε(t)为服从零均值多维正态分布的随机误差,其协方差矩阵记为Γ(t)。
测量数据的全部采样时刻记为t1,t2,…,tM,对应的轨迹参数记为X=(x(t1),x(t2),…,x(tM))T。轨迹参数估计就是融合所有时刻的测量数据y(t1),y(t2),…,y(tM)给出X的高精度估计,从而确定飞行器完整的运动轨迹。对测量数据作归一化处理,令
Y=(Γ-1/2(t1)y(t1),Γ-1/2(t2)y(t2),…,
Γ-1/2(tM)y(tM))T
E=(Γ-1/2(t1)ε(t1),Γ-1/2(t2)ε(t2),…,
Γ-1/2(tM)ε(tM))T
F(X)=(Γ-1/2(t1)f(x(t1)),Γ-1/2(t2)f(x(t2)),…,
Γ-1/2(tM)f(x(tM)))T
则有
Y=F(X)+E
(3)
其中,E服从多维标准正态分布。对X的准确估计采用如下非线性最小二乘估计:
在某些时刻点如果没有足够多的测量(3个位置测元和3个速度测元)解算6个轨迹参数,就出现了不完全测量的情况,由于测量的数量少于待估参数的数量,上述最小二乘估计模型是病态的,其解可能不唯一,即使能确定唯一解,但由于误差传播过大而使得求解结果在数值上不稳定,难以给出有效的轨迹参数估计。解决不完全测量问题一个重要途径是通过物理机理分析、从历史数据挖掘先验信息等,寻求待估参数的稀疏表示,以降低模型解空间的维数,改善问题的病态性。通过对飞行器运动特性和大量实际轨迹数据的分析发现,采用B样条函数表示轨迹参数能够在保证精度的前提下大幅度减少待估参数。
将轨迹参数表示为如下n+1阶B样条函数:
(4)
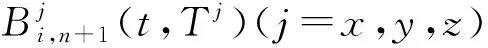
则式(4)表示为:
x(t)=B(t,T)β
令B(T)=(B(t1,T),B(t2,T),…,B(tM,T))T,于是,式(3)变换为:
Y=F(B(T)β)+E
这样轨迹参数X的估计转化为样条节点T和样条系数β的估计:
(5)
待估参数T和β的数量显著小于X的数量。
为进一步减少待估参数的数量,可将稀疏性约束(非零待估参数的数量最少)加入优化模型(5)中,构造如下稀疏表示寻优模型:
(6)
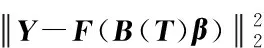
模型(6)在估计样条系数β的同时,需确定样条节点序列T,模型的非线性程度非常高,计算量太大,难以获得全局最优解。可以先由粗略的轨迹参数预先确定样条节点T*,然后再估计样条系数。事实上,样条节点数决定了样条系数的数量,从而决定了待估参数的数量,因此,T*的选取应在保证较小的拟合误差的前提下,尽量压缩其数量,以改善估计模型的病态性。第2节将给出一种基于稀疏优化的样条节点选取方法,能够大幅度减少样条节点数。确定T*后,只需估计样条系数,即求解优化问题:
(7)
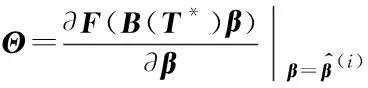
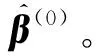
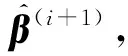
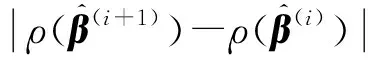
2 基于稀疏优化的样条节点选取
样条节点的选取应依据轨迹参数的动力学特性,在变化剧烈、可微性较差的轨迹段落(例如级间段)节点分布较为密集,在变化平缓的段落节点分布较为稀疏。遥测轨迹参数源于飞行器平台系统的加速度表测量,其动力特征与飞行器的实际运动轨迹具有很好的一致性[5],可作为确定样条节点的粗略轨迹参数。下面只给出x方向的样条节点确定方法,y和z方向的方法相同。
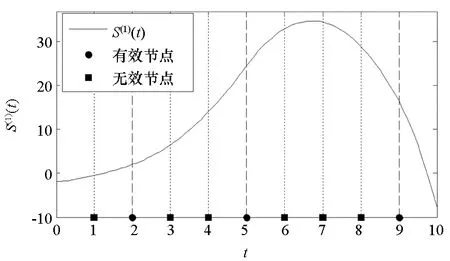
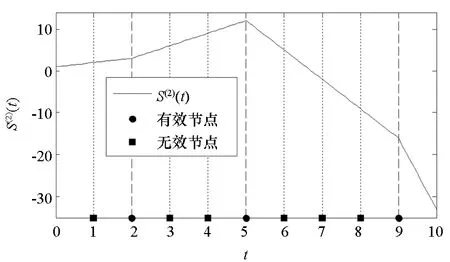
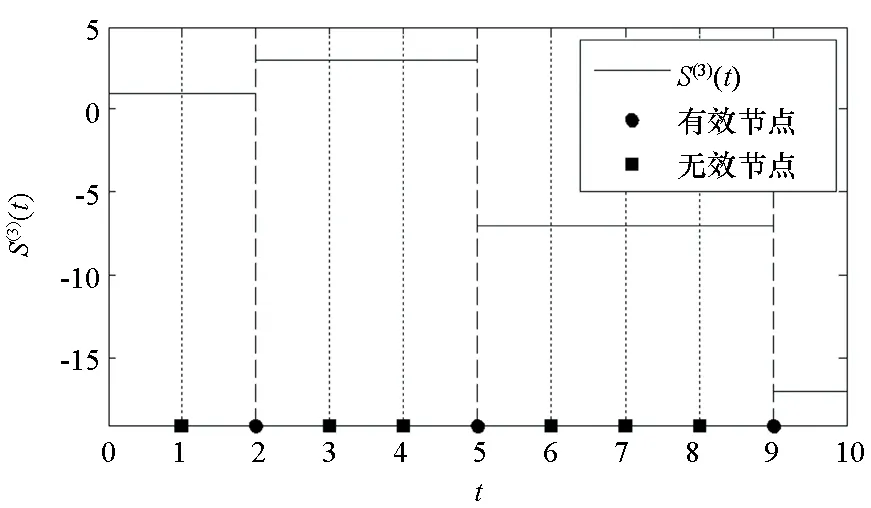
2.1 样条节点的稀疏优化模型
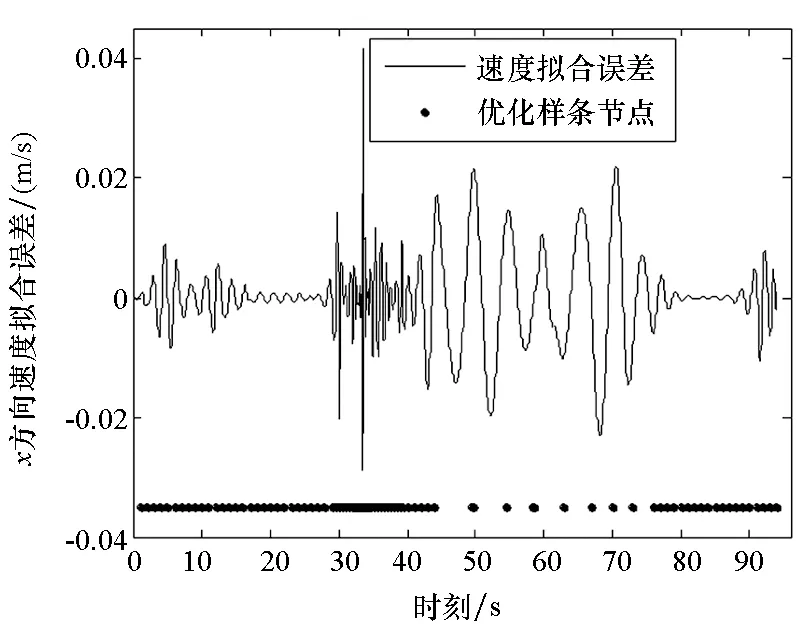
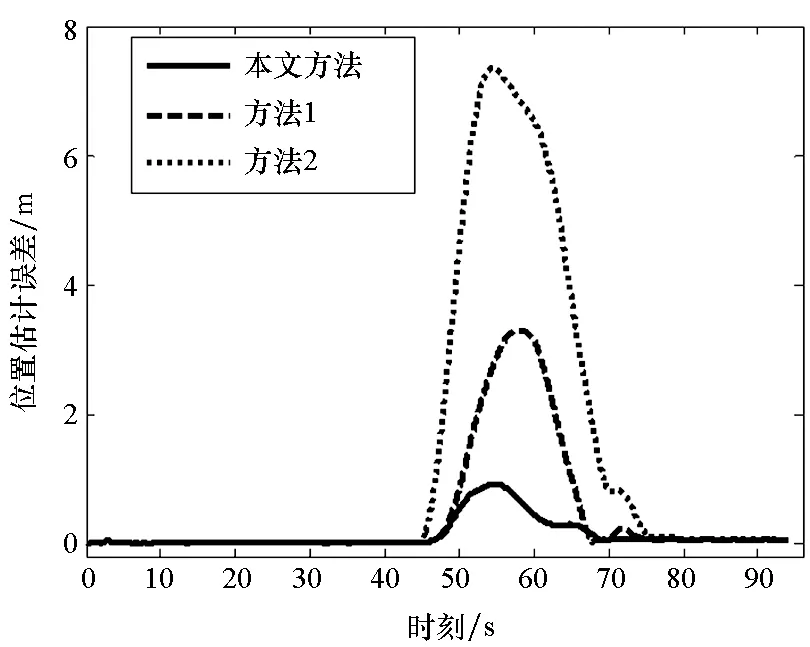
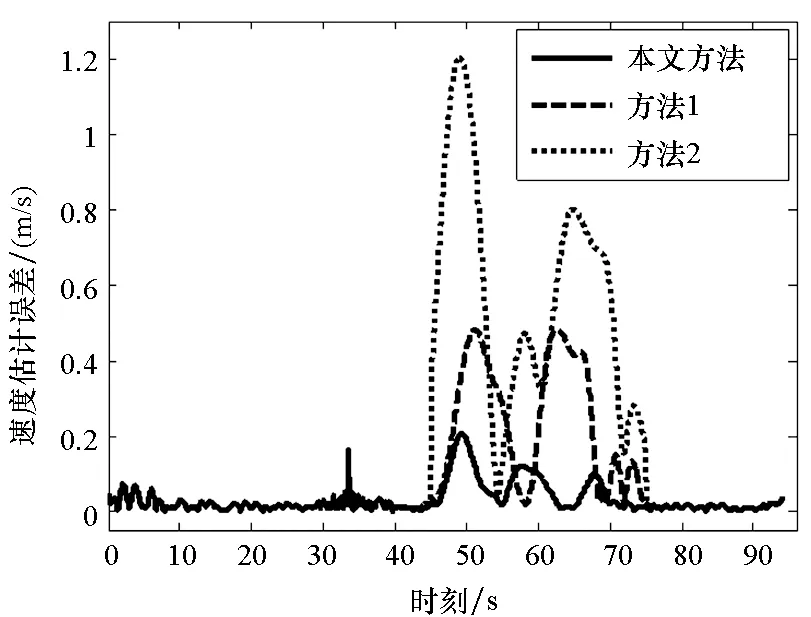
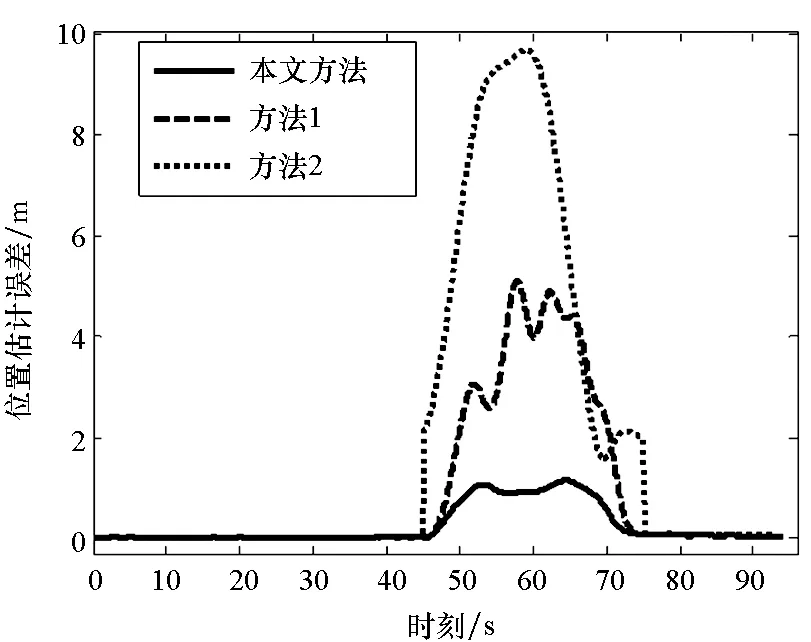
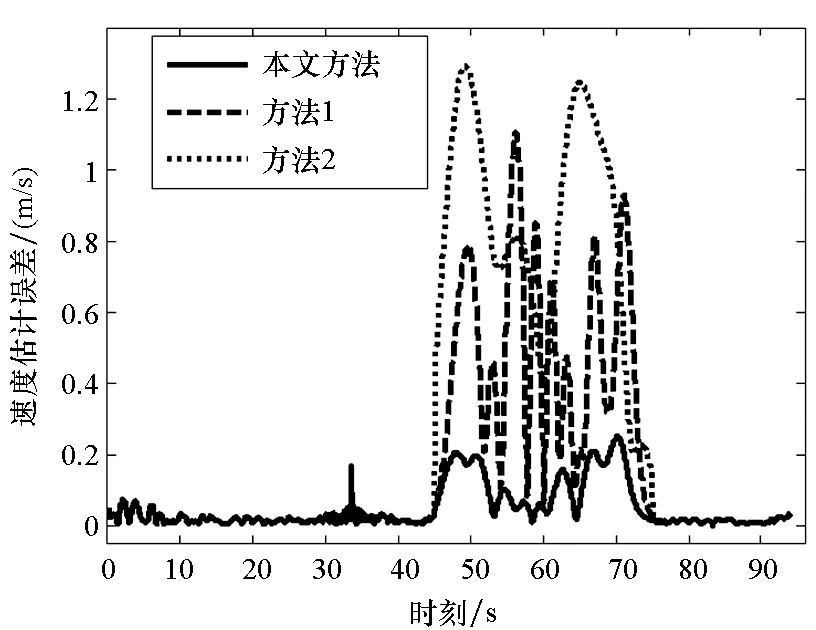
给定区间[a,b]上的扩充分划η:τ-n<τ-n+1 (8) 其中,bi为常值样条系数,τi(i=1,2,…,N-1)称为内节点序列。S(t)是[a,b]上的n-1阶连续可微函数,n阶导函数S(n)(t)为分段常值函数,其不连续点全部位于内节点序列中。关于S(n)(t)不连续的内节点称为有效节点,连续的内节点称为无效节点。无效节点是冗余的,即删除无效节点后,不会改变样条函数值。为减少样条节点的数量,应去除无效节点,并且最大限度压缩有效节点的数量。图1为一个包含9个内节点的四阶B样条函数及其前三阶导数的曲线图,内节点中包括6个无效节点和3个有效节点,可以看出,三阶导数为阶梯函数,其不连续点位于3个有效节点处。 (a) 四阶B样条函数S(t)(a) Four order B-spline S(t) (b) 一阶导数S(1)(t)(b) The first order derivative S(1)(t) (c) 二阶导数S(2)(t)(c) The second order derivative S(2)(t) (d) 三阶导数S(3)(t)(d) The third order derivative S(3)(t)图1 四阶B样条函数及其前三阶导数Fig.1 A four order B-spline and its first three derivatives θ=(b-n,b-n+1,…,bN-1)T 则D中的非零元对应于S(n)(t)的不连续点,即有效节点。为压缩有效节点数,应在保证S(t)对r和v的拟合误差不超过允许值的条件下,使D中的非零元素尽量少,即建立如下稀疏优化模型: (9) 其中,δ1和δ2为设定的位置和速度拟合误差门限,δ1>0,δ2>0。 为保证模型(9)存在可行解并且D具有稀疏性,应选取密集的初始样条节点η,求解模型后,将无效节点从η中删除,剩余的有效节点即为所需的优化样条节点。本文采用节点加密方法确定初始样条节点,步骤为: 步骤1:取较为密集的等距样条节点序列η。 步骤3:对η′按距离聚类,把每一类各节点间的中点加入节点序列η中,转到步骤2。 下面给出模型(9)的凸优化求解方法。 为求解模型(9),需要获得D关于θ的函数表达式。事实上,D是关于θ的线性函数,可将模型(9)转化为线性凸优化问题,便能够利用多项复杂度的凸优化方法完成模型求解。为确定D关于θ的函数表达式,给出如下定理: 定理n+1阶B样条函数S(t)的k阶导数S(k)(t)(1≤k≤n)在[a,b]上满足: (10) 其中, (11) 下面采用数学归纳法完成该定理的证明。 证明:Bi,n+1(t)满足如下微分关系[2]: (12) 当k=1时,由式(8)和式(12)得: 当t∈[a,b]时,B-n,n(t)≡0,BN,n(t)≡0,于是 定理成立。 假设当k=j时定理成立,当k=j+1时,由式(10)和式(12)得: 当t∈[a,b]时,B-n+j,n-j(t)≡0,BN,n-j(t)≡0,式(11)成立,则有: Bi,n+1-(j+1)(t) 定理得证。 □ 由定理得知: 而 于是对于i=1,…,N-1,有: (13) 由式(11)和式(13)知,D与θ存在线性关系D=Cθ,其中C为(N-1)×(N+n)阶的矩阵。这样,模型(9)转化为约束优化问题: 但上述最小化l0范数为NP难解问题,可用l1范数代替l0范数,转化为线性凸优化问题: (14) 可利用具有多项式复杂度的凸优化方法[14]求解。 飞行器的真实轨迹参数由动力学方程[15]积分产生,时长为94 s,轨迹中含有一个级间段,位于33.4 s附近。由9台连续波雷达(测元为距离和径向速度)和4台光学设备(测元为方位角和俯仰角)对飞行器跟踪测量,仿真测量数据由测量真值加随机误差构成,其中,连续波雷达的测距精度为8.3 m,测速精度为0.05 m/s,光学设备方位角和俯仰角的测量精度都为5″。设置两个不完全测量场景:场景1的不完全测量段落为45 s—75 s的轨迹平稳段,该时间段只有2台连续波雷达的2个距离和2个径向速度测元,其余时间所有设备的测量数据完好;场景2的不完全测量段落也是45 s—75 s,该时间段只有1台光学设备的1个俯仰角和1个方位角测元。 采用5阶B样条函数表示轨迹参数,利用2.1节中的节点加密方法确定x、y和z三个方向遥测轨迹的初始样条节点,拟合误差门限取为σ1=0.1 m,σ2=0.05 m/s,不完全测量段落的初始节点距取为0.2 s,其余段落的初始节点距取为 1 s。经过3~4次节点加密即可使拟合误差小于门限值,x、y和z三个方向加密后的内节点数分别为237、239和213。图2和图3给出了x方向初始样条节点的分布以及位置、速度的拟合误差,可见,节点加密部分主要位于级间段,节点加密后的拟合误差满足门限设置要求。 图2 x方向的初始样条节点和位置拟合误差Fig.2 Initial knots of spline and fitting errors of position for x-coordinate 由不完全测量段落(45 s—75 s)的初始样条节点建立稀疏优化模型,模型中的拟合误差门限取为δ1=0.1 m,δ2=0.05 m/s,利用CVX凸优化程序包[16]对模型进行求解,x、y和z三个方向剔除节点的|Cθ|阈值都取为1E-5,三个方向上优化后的样条内节点数分别为95、96和62,明显少于初始内节点数。图4和图5为x方向稀疏优化后的样条节点分布以及位置、速度的拟合误差,可以看出,不完全测量段落的样条节点分布稀疏,拟合误差未超出门限。 图3 x方向的初始样条节点和速度拟合误差Fig.3 Initial knots of spline and fitting errors of velocity for x-coordinate 图4 x方向的优化样条节点和位置拟合误差Fig.4 Optimized knots of spline and fitting errors of position for x-coordinate 图5 x方向的优化样条节点和速度拟合误差Fig.5 Optimized knots of spline and fitting errors of velocity for x-coordinate 利用上述稀疏优化后的样条节点结合测量数据估计轨迹参数。将本文方法的估计结果与文献[5]提出的基于轨迹动力特征的估计方法(方法1)、基于多项式模型的估计方法(方法2)进行比较,其中,方法2采用三个多项式表示x、y和z三个方向的轨迹参数,由测量数据优化求解多项式系数,用以确定不完全测量段落的轨迹参数,方法2在完全测量段落的估计方法与方法1相同。 图6和图7分别是场景1位置和速度估计误差的对比图,可以看出,本文方法在不完全测量段落对轨迹参数的估计精度相对方法1和方法2都有大幅度的提高,方法1在不完全测量段落的位置和速度平均误差分别为1.33 m和0.240 m/s,方法2的平均误差为3.91 m和0.573 m/s,而本文方法的平均误差只有0.38 m和0.067 m/s。场景2位置和速度估计误差的对比见图8和图9,可见,本文方法相对方法1和方法2仍然能够大幅度提高不完全测量段落的轨迹参数估计精度,本文方法在不完全测量段落的位置和速度平均误差为0.74 m和0.117 m/s,而方法1的平均误差达到了2.73 m和0.471 m/s,方法2的平均误差达到了5.74 m和0.823 m/s。本文方法、方法1和方法2在不完全测量段落待估参数的数量分别为17、29和20。本文方法相对方法1能够提高估计精度,是因为通过样条节点的稀疏优化大幅度减少了待估参数的数量,缓解了模型的病态性;方法2待估参数的数量虽然也较少,但用多项式表示轨迹参数引入了较大的截断误差,估计精度低。场景2的估计误差相对场景1较大,这是由于场景2在不完全测量段落的测量数据数量比场景1更少。 图6 场景1位置估计误差Fig.6 Errors of position estimates in scenario 1 图7 场景1速度估计误差Fig.7 Errors of velocity estimates in scenario 1 图8 场景2位置估计误差Fig.8 Errors of position estimates in scenario 2 图9 场景2速度估计误差Fig.9 Errors of velocity estimates in scenario 2 研究不完全测量条件下的飞行器轨迹参数估计问题,提出了一种基于稀疏优化的轨迹参数估计新方法。利用B样条函数给出轨迹参数的稀疏表示,建立了估计轨迹参数的寻优模型;依据样条函数高阶导数在节点处的不连续性,将表示样条的节点划分为有效节点和无效节点两类,模型待估参数的数量取决于有效节点的数量;采用稀疏优化方法最大限度压缩样条的有效节点数,从而减少待估参数的数量,改善模型的病态性。仿真结果表明,在不完全测量段落,稀疏优化方法相对已有的基于轨迹动力特征的估计方法能够大幅度提高轨迹参数的估计精度。本文的方法没有考虑测量设备的系统误差,下一步将研究不完全测量条件下的轨迹参数和系统误差的联合估计方法,实现系统误差自校准。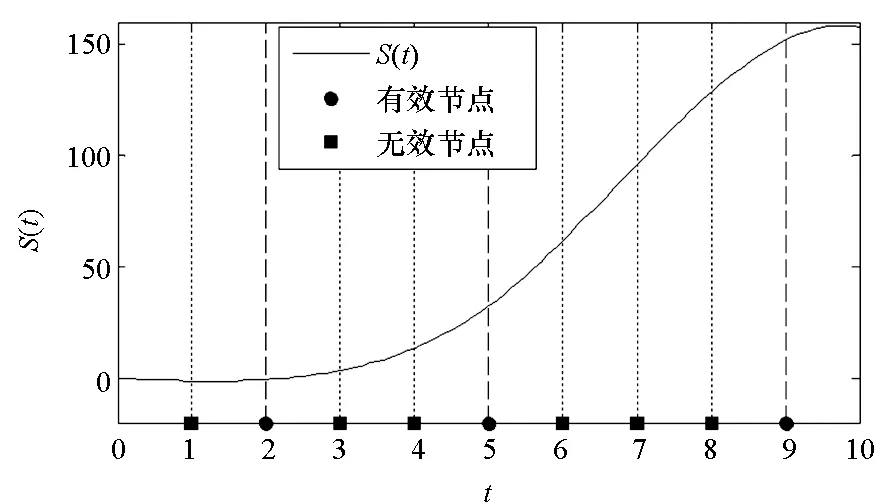

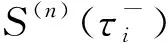
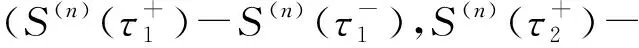
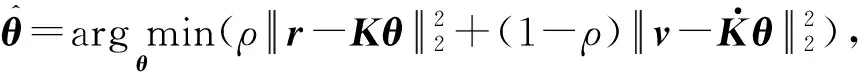
2.2 稀疏优化模型的求解方法
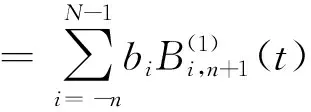
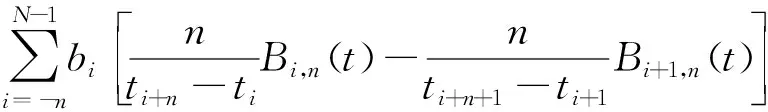
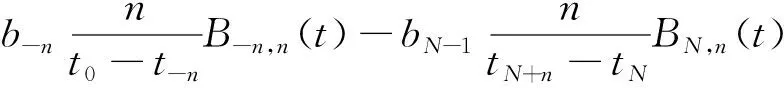
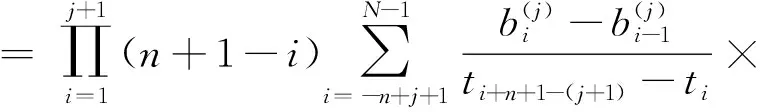
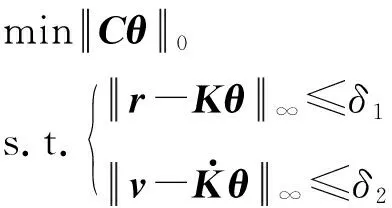
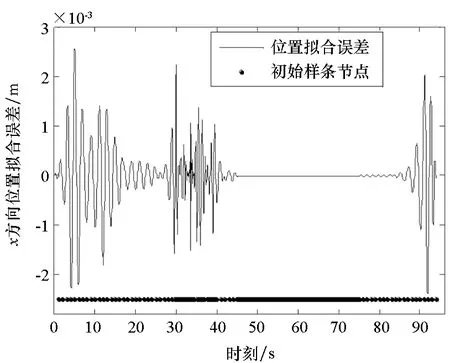
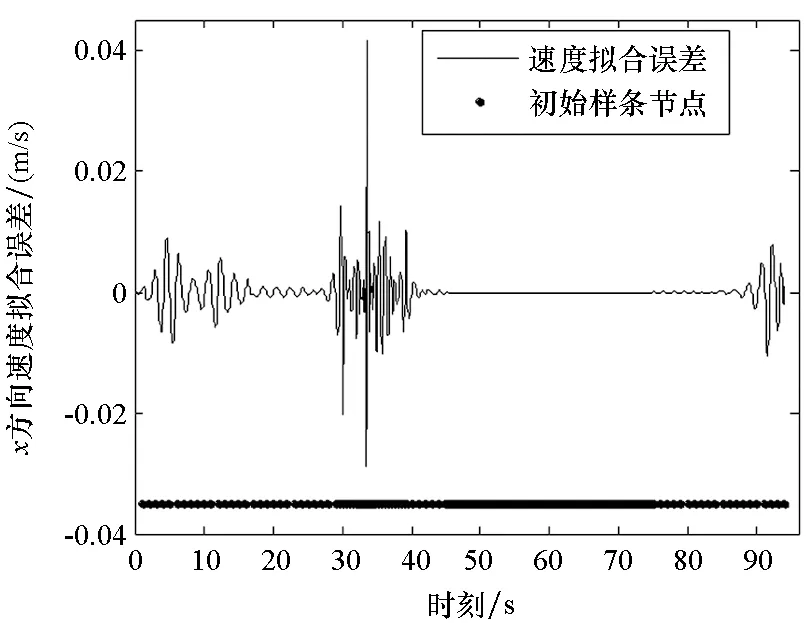
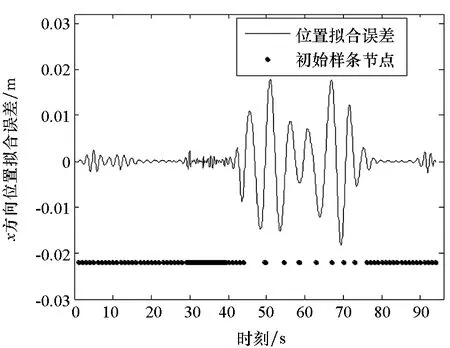
3 仿真实验与结果分析
4 结论
