隧道衬砌裂缝对结构受力的影响规律研究

杨志刚，周智辉 ，凌同华，吴维祥，陈俭华

(1.中铁南方投资集团有限公司，广东 深圳 518000；2.长沙理工大学 土木工程学院，湖南 长沙 410114；3.深圳市地铁集团有限公司，广东 深圳 518026)

随着中国交通基础设施建设的高速发展，隧道工程作为路网建设中不可或缺的一部分，也取得了极大的发展[1−3]，隧道数量和里程逐年增加，隧道衬砌质量的安全问题也伴随而来，引起了学者们的注意[4−5]。隧道二次衬砌裂缝是对结构有重大影响的典型病害[6−8]，很多学者针对隧道裂缝展开了研究。王华牢[9]等人结合安吉隧道对带裂缝的隧道进行了调查，提出了通过裂缝数量划分隧道安全等级。叶飞[10]等人通过对新建高速公路隧道裂缝进行统计调查，仔细分析了裂缝产生的原因，并提出了对隧道裂缝进行三维监测的思路。黄宏伟[11]等人通过对某地公路隧道的数值模拟与实测结果的对比，论证了采用扩展有限元模拟隧道衬砌开裂及裂缝扩展的可行性。李庆桐[12]等人采用数字图像处理方法对裂缝病害信息进行量化分析，根据裂缝病害量化参数，通过聚类和回归分析等手段，依次建立了病害分级档数、病害诊断指标(tunnel defect indexcrack，简称为TDI-C)及病害等级的分级标准，实现了隧道裂缝病害严重程度评定。余晶[13]依托工程检测进行现场裂缝取芯和地质雷达检测，构建了衬砌通缝模型，通过比较受拉受压强度标准值，发现了裂缝的产生会对相应部位产生较大影响，使其安全性能降低。

目前，学者对隧道衬砌裂缝深度的影响及防治方面研究较多，但对裂缝宽度研究较少。衬砌裂缝对结构承载力和安全性能的影响尚未进行系统研究。因此，作者拟运用有限元软件建立隧道衬砌结构裂缝宽度模型，通过改变隧道裂缝深度和宽度，探索裂缝对衬砌结构敏感部位的影响，以期为实际工程安全施工和健康运营提供指导。

1 工程概况

深圳6 号线地铁银−八区间分布工况为：北接银湖站、南至八卦岭站。银湖站至八卦岭站区间，左线的设计里程为ZDK6+119.048～ZDK6+897.212，短链6.813 m，左线全长771.351 m，其中，ZDK6+783.258～ZDK6+897.212 共113.954 m，已由9 号线工程同期设计并施工。6 号线左线二期的工程土建设计范围为ZDK6+119.048～ZDK6+783.258，共664.210 m。右线的设计里程为YDK6+119.048～YDK6+893.212，全长774.164 m，其中，YDK6+738.258～YDK6+893.212 共154.954 m，已由9 号线工程同期设计和施工。6 号线右线二期的土建设计范围为 YDK6+119.048 ～YDK6+738.258，共619.210 m。

区间从银湖站沿北环大道东侧向南出发，沿线穿越四季青花园、泥岗中学、展览中心、泥岗西路立交等建/构筑物到达八卦岭站。泥岗中学处设置盾构始发井，采用矿山法向银湖站方向施工；采用盾构法向八卦岭站方向施工。区间隧道埋深为30 m。

2 计算模型

2.1 计算参数

采用Midas 有限元软件对隧道区间裂缝进行模拟，隧道围岩为Ⅴ级。根据该工程实际情况，地基围岩弹性抗力系数取31.616 MPa/m。地基弹簧只承受压力荷载，不承受拉力荷载[14−15]。隧道设计为区间隧道，衬砌厚度40 cm，衬砌为素混凝土，混凝土标号C35。该模型的材料参数为：弹性模量取31.5 GPa，泊松比取0.2，重度取25 kN/m3。

2.2 围岩压力计算

深、浅埋隧道的分界深度，按荷载等效高度值、工程地质条件、施工方法等因素综合判定。荷载等效高度计算式为[16]：

式中：HP为深浅埋隧道的分界深度；hq为荷载等效高度值。

荷载等效高度按式(2)计算：

其中，q=0.45×2s−1γw，为均布荷载压力，kN/m2；w=1+i(B−5)，为宽度影响系数。

式中：γ 为围岩重度，kN/m3；s 为围岩级别；B 为隧道宽度，取值为5.2 m；i 为B 每增减1 m 时的围岩压力增减率，当B＞5 m 时，取i=0.1。

根据隧道工况，围岩为Ⅴ级，将参数代入式(1)～(2)，可计算出宽度影响系数ω=1.02，围岩压力q竖向=q=139.54 kPa，围岩水平均布压力e=q水平=(0.3～0.5)q=55.80 kPa。经过计算可得：竖直土压力荷载为q竖向=q=139.54 kPa，水平均布压力取e=q水平=55.80 kPa。

2.3 计算模型示意图

隧道断面为C 形支护断面如图1 所示，隧道上部衬砌半径R=2 600 mm，其分布角度为150°，仰拱部位采用半径为R=3 970 mm 的圆弧，圆弧分布角度为41°15′34″。隧道墙脚部位采用圆弧半径为R=5 200 mm，分布的角度为左、右各26°37′17″。

3 结果分析

3.1 裂缝深度对衬砌结构的影响

为了探索裂缝深度对结构受力的影响，基于工程地质实际情况，在实际荷载作用下，根据设计文件，建立了隧道结构模型。隧道二衬模型厚40 cm，根据围岩地质特征，划分为Ⅴ级围岩，埋深30 m。由于结构的对称性，因此，只对结构拱顶、拱肩、中墙和墙脚等具有典型代表性的敏感部位进行裂缝缺陷设置和受力计算分析。

3.1.1 拱顶位置不同深度裂缝的数值模拟

设计了不同深度裂缝缺陷的3 种工况进行模拟。其中，工况1～3 裂缝深度分别10～30 cm。

图1 隧道衬砌断面图Fig.1 Cross section of tunnel lining

工况1：拱顶存在10 cm 裂缝时，衬砌结构弯矩和剪力云图如图2 所示。

工况2：拱顶存在20 cm 裂缝时，衬砌结构弯矩和剪力云图如图3 所示。

工况3：拱顶存在30 cm 裂缝时，衬砌结构弯矩和剪力云图如图4 所示。

图2 裂缝10 cm 时衬砌结构弯矩和剪力云图Fig.2 Bending moment and shear diagram of lining structure with 10 cm crack at vault

图3 裂缝20 cm 时衬砌结构弯矩和剪力云图Fig.3 Bending moment and shear diagram of lining structure with 20 cm crack at vault

从图2～4 中可以看出，当裂缝发生在拱顶时，隧道衬砌周边弯矩呈对称性分布，仰拱部位出现最大正弯矩值，中墙位置出现最大负弯矩值；剪力在左、右墙脚位置呈现出反对称分布，左墙脚出现最大负剪力，右墙脚出现最大正剪力。当裂缝宽度为10 cm 时，裂缝处单元所受弯矩为33.1 kN·m，所受剪力为−15.1 kN；当裂缝宽度为20 cm 时，裂缝处单元所受弯矩为43.4 kN·m，所受剪力为−34.5 kN；当裂缝宽度为30 cm 时，裂缝处单元所受弯矩为29.9 kN·m，所受剪力为−15.5 kN。

3.1.2 拱肩位置不同深度裂缝的数值模拟

工况1：右拱肩存在10 cm 裂缝时，衬砌结构弯矩和剪力云图如图5 所示。

工况2：右拱肩存在20 cm 裂缝时，衬砌结构弯矩和剪力云图如图6 所示。

工况3：右拱肩存在30 cm 裂缝时，衬砌结构弯矩和剪力云图如图7 所示。

从图5～7 中可以看出，当衬砌裂缝位于右拱肩位置时，隧道衬砌周边弯矩和剪力都出现了不对称分布，弯矩在拱顶和仰拱位置出现最大值，在左边墙脚出现最大负弯矩；剪力在右边墙脚出现最大值，在左边墙脚出现最大负剪力。当裂缝宽度为10 cm 时，裂缝处单元所受弯矩为−26.3 kN·m，所受剪力为−127.9 kN；当裂缝宽度为20 cm 时，裂缝处单元所受弯矩为−32.5 kN·m，所受剪力为−127.8 kN；当裂缝宽度为30 cm 时，裂缝处单元所受弯矩为37.1 kN·m，所受剪力为−127.4 kN。

图4 裂缝30 cm 时衬砌结构弯矩和剪力云图Fig.4 Bending moment and shear diagram of lining structure with 30 cm crack at vault

图5 拱肩裂缝10 cm 时衬砌结构弯矩和剪力云图Fig.5 Bending moment and shear diagram of lining structure with 10 cm crack at spandrel

图6 拱肩裂缝20 cm 时衬砌结构弯矩和剪力云图Fig.6 Bending moment and shear diagram of lining structure with 10 cm crack at spandrel

3.1.3 中墙位置不同深度裂缝的数值模拟

工况1：中墙存在10 cm 裂缝时，衬砌结构弯矩和剪力云图如图8 所示。

工况2：中墙存在20 cm 裂缝时，衬砌结构弯矩和剪力云图如图9 所示。

工况3：中墙存在30 cm 裂缝时，衬砌结构弯矩和剪力云图如图10 所示。

从图8～10 中可以看出，当裂缝发生在右边中墙位置时，隧道衬砌周边弯矩大致呈对称性分布，拱顶和仰拱部位正弯矩达到最大值，左边墙脚负弯矩达到最大值；剪力在左、右墙脚位置呈现出不对称分布，左墙脚出现最大负剪力，右墙脚出现最大正剪力。当裂缝宽度为10 cm 时，裂缝处单元所受弯矩为−32.3 kN·m，所受剪力为−127.9 kN；当裂缝宽度为20 cm 时，裂缝处单元所受弯矩为−19.7 kN·m，所受剪力为−127.9 kN；当裂缝宽度为30 cm 时，裂缝处单元所受弯矩为−18.0 kN·m，所受剪力为−127.4 kN。

3.1.4 墙脚位置不同深度裂缝的数值模拟

工况1：墙脚存在10 cm 裂缝时，衬砌结构弯矩和剪力云图如图11 所示。

工况2：墙脚存在20 cm 裂缝时，衬砌结构弯矩和剪力云图如图12 所示。

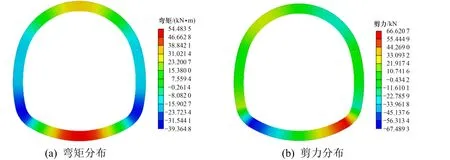
图7 拱肩裂缝30 cm 时衬砌结构弯矩和剪力云图Fig.7 Bending moment and shear diagram of lining structure with 10 cm crack at spandrel

图8 中墙裂缝10 cm 时衬砌结构弯矩和剪力云图Fig.8 Bending moment and shear diagram of lining structure with 10 cm crack at sidewall

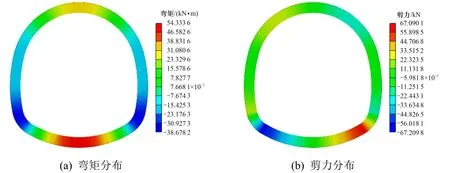
图9 中墙裂缝20 cm 时衬砌结构弯矩和剪力云图Fig.9 Bending moment and shear diagram of lining structure with 10 cm crack at sidewall

工况3：墙脚存在30 cm 裂缝时，衬砌结构弯矩和剪力云图如图13 所示。

图11～13 中可以看出，当裂缝发生在右边墙脚时，隧道衬砌周边弯矩呈对称性分布，剪力呈反对称分布。左边墙脚出现最大负剪力，右边墙脚出现最大正剪力，弯矩最大值发生在仰拱位置。随着裂缝深度的扩大，结构剪力最大值逐渐增大，而弯矩最大值保持不变。当裂缝宽度为10 cm 时，裂缝处单元所受弯矩为−28.3 kN·m，所受剪力为−144.7 kN；裂缝宽度为20 cm 时，裂缝处单元所受弯矩为−35.3 kN·m，所受剪力为−144.6 kN；当裂缝宽度为30 cm 时，裂缝处单元所受弯矩为−40.3 kN·m，所受剪力为−144.1 kN。

3.2 裂缝宽度对结构受力特征的影响

拱顶、拱肩、中墙和墙脚的宽度为10 mm 和深度为20 cm 的深裂缝时，衬砌结构弯矩和剪力云图如图14～17 所示。当拱顶、拱肩、中墙和墙脚分别存在宽度为10 mm、深度为20 cm 的深裂缝时，衬砌结构弯矩及剪力分布情况大致相同，在拱顶及仰拱位置出现最大正弯矩值，最大负弯矩值出现在左右拱脚位置，剪力最大值发生在左拱肩及右拱脚位置，剪力最小值出现在左拱脚处。当裂缝存在于拱顶位置时，结构所受的弯矩及剪力值最大，即：相对于裂缝存在于拱肩、中墙和墙脚的情况，当同样尺寸的裂缝发生于拱顶位置时，结构更容易发生破坏，发生危险的可能性更大。

图10 中墙裂缝30 cm 时衬砌结构弯矩和剪力云图Fig.10 Bending moment and shear diagram of lining structure with 10 cm crack at sidewall

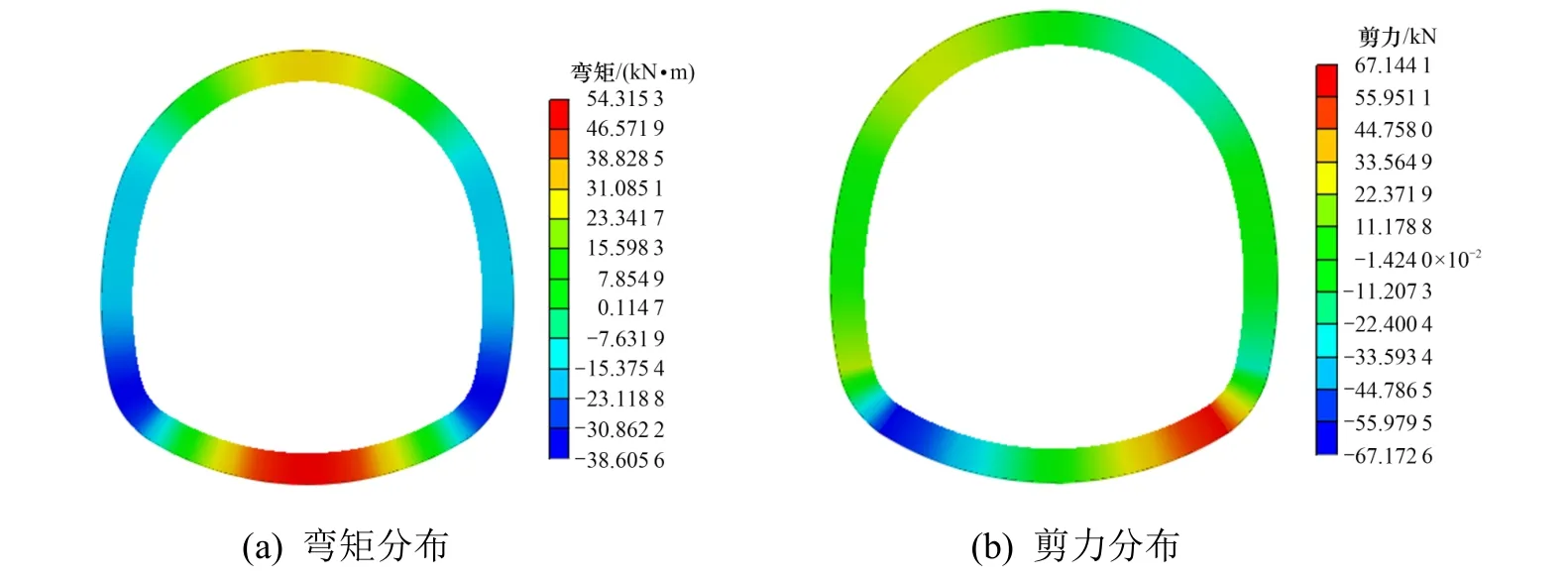
图11 墙脚裂缝10 cm 时衬砌结构弯矩和剪力云图Fig.11 Bending moment and shear diagram of lining structure with 10 cm crack at arch foot

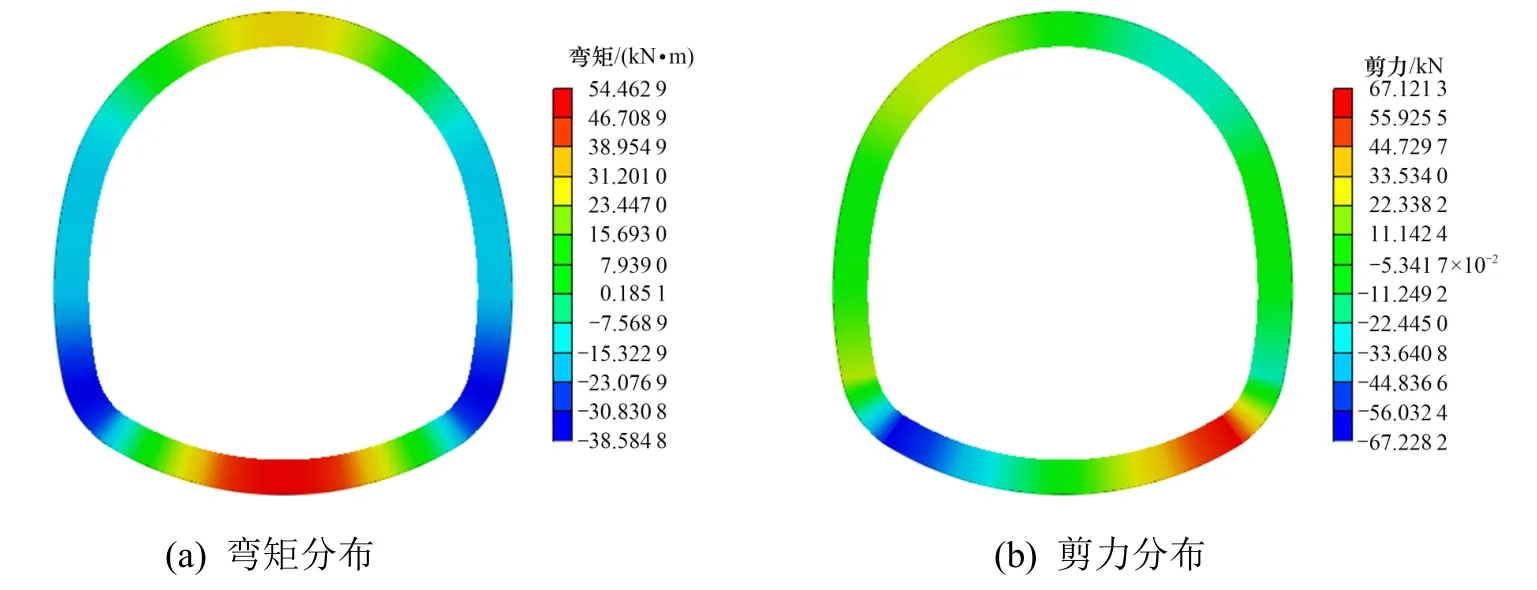
图12 墙脚裂缝20 cm 时衬砌结构弯矩和剪力云图Fig.12 Bending moment and shear diagram of lining structure with 20 cm crack at arch foot

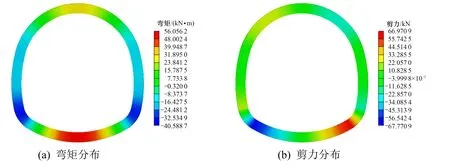
图13 墙脚裂缝30 cm 时衬砌结构弯矩和剪力云图Fig.13 Bending moment and shear diagram of lining structure with 30 cm crack at arch foot

图14 拱顶裂缝衬砌结构弯矩和剪力图Fig.14 Bending moment and shear diagram of lining structure with crack at vault

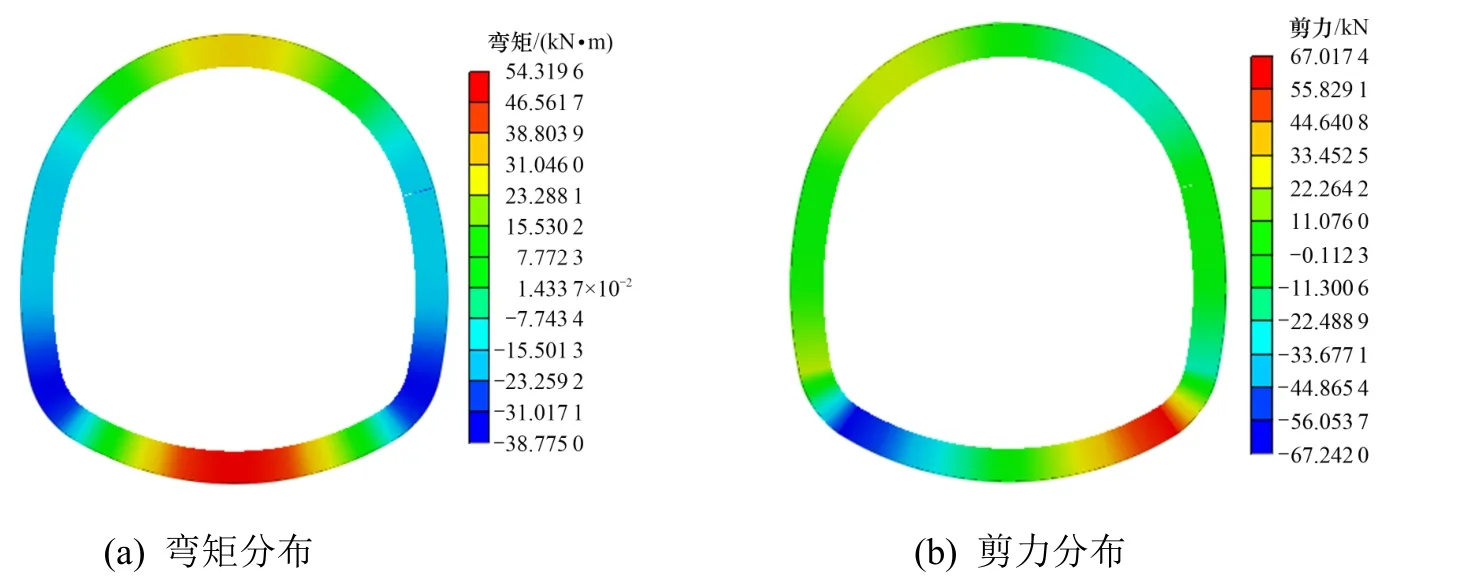
图15 拱肩裂缝衬砌结构弯矩和剪力图Fig.15 Bending moment and shear diagram of lining structure with crack at spandrel

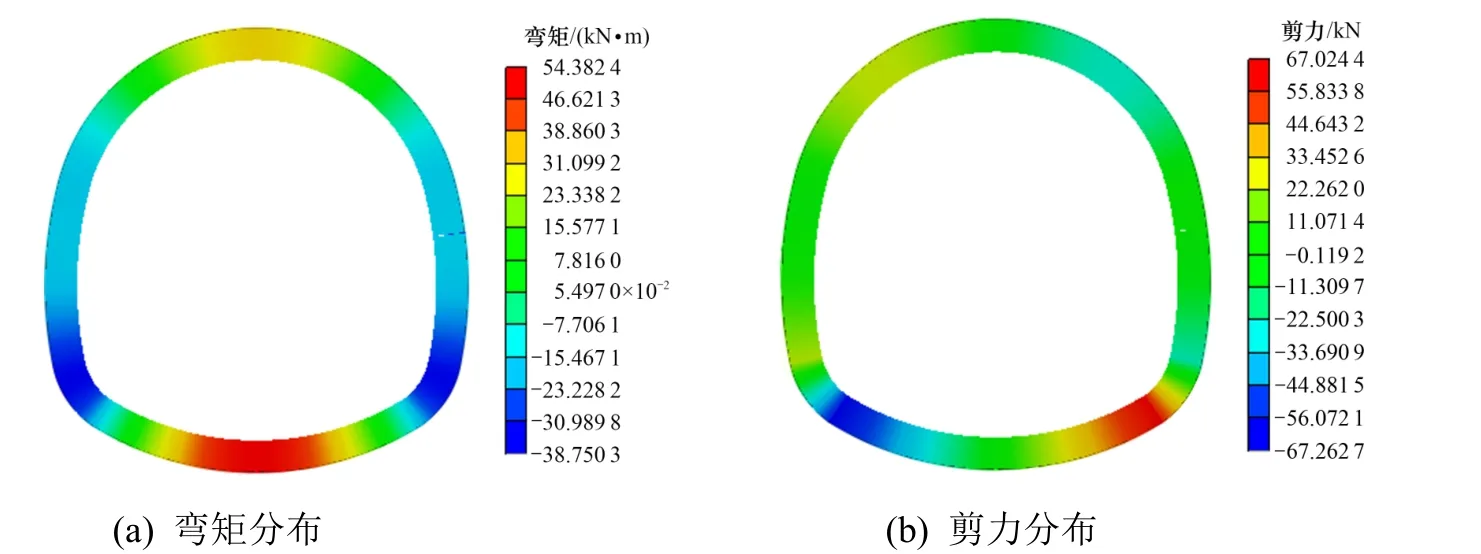
图16 中墙裂缝衬砌结构弯矩和剪力图Fig.16 Bending moment and shear diagram of lining structure with crack at sidewall

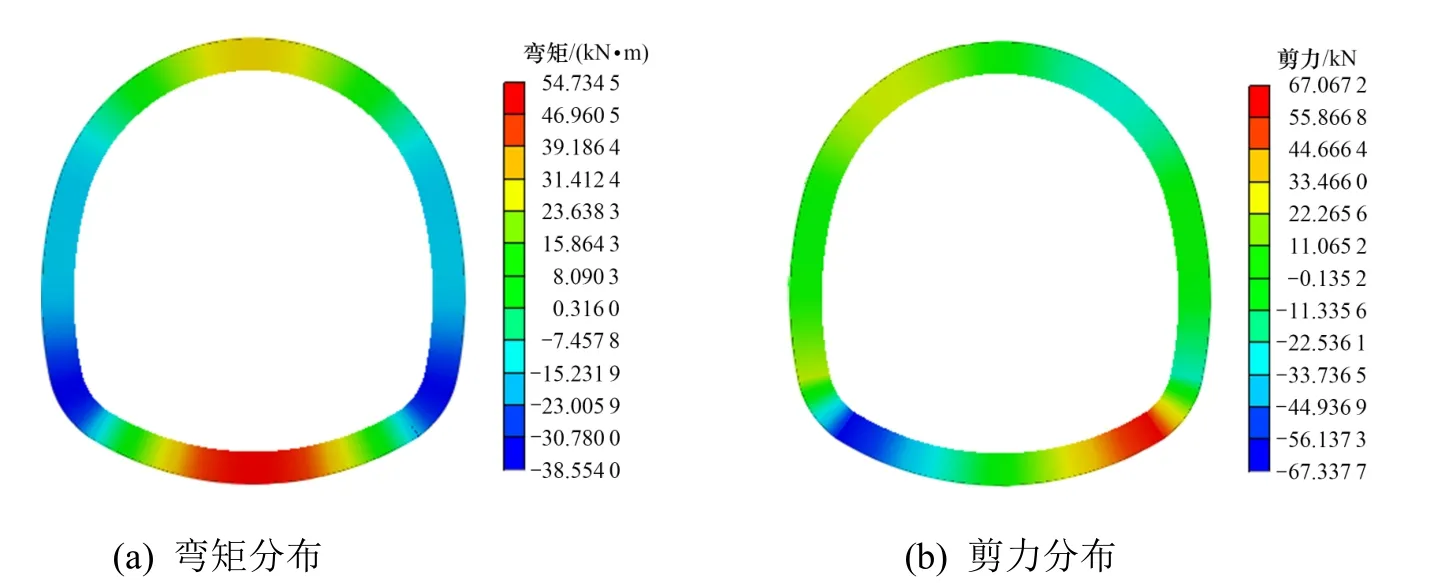
图17 墙脚深裂缝衬砌结构弯矩和剪力Fig.17 Bending moment and shear diagram of lining structure with crack at arch foot

为分析裂缝宽度对结构承载力的影响，设置裂缝深度为20 cm，裂缝宽度分别设置为5,10,15,20,25,30 mm 6 种工况分析结构的受力特点。如图18～21 所示。

从图18 中可以看出，弯矩随着裂缝的扩张，在衬砌范围内随之发生变化。当拱顶裂缝宽度由5 mm 扩张到10 mm 时，对单元受力结构影响最明显。由于裂缝宽度的扩张，影响了结构弯矩的重分布，致使拱腰、中墙、墙脚、仰拱等部位弯矩减小。当裂缝扩张到10 mm 之后，结构弯矩随着裂缝再次扩张影响不明显。

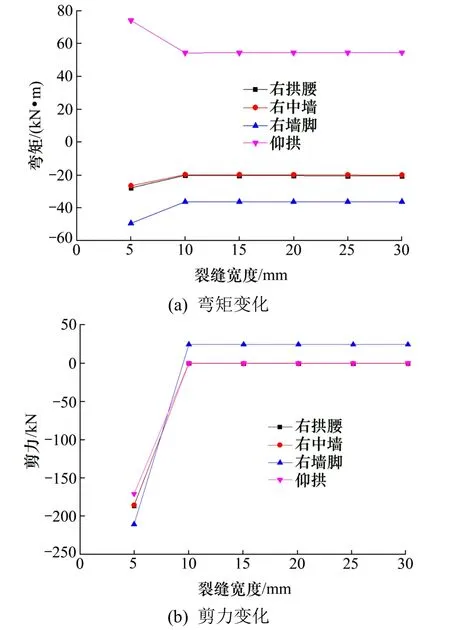
图18 衬砌典型位置处弯矩和剪力随拱顶裂缝宽度增加的变化情况Fig.18 Variation of bending moment and shear at the characteristic position of lining with increasing crack width at vault

衬砌剪力随着裂缝扩张，也随之发生变化，其变化规律和弯矩变化规律相近。当拱顶裂缝宽度由5 mm 扩张到10 mm 时，对单元受力结构影响最明显，剪力迅速减小；当裂缝扩张到10 mm 之后，结构的剪力随着裂缝的扩张，影响不明显。

图19 衬砌典型位置处弯矩和剪力随拱肩裂缝宽度增加的变化情况Fig.19 Variation of bending moment and shear at the characteristic position of lining with the increasing of crack width at spandrel

从图19 中可以看，当裂缝在拱肩处时，裂缝横向扩张对衬砌内典型结构处弯矩影响不明显。拱肩处裂缝横向扩张引起了剪力改变，5～10 mm 处变化最明显，随着裂缝的扩张影响不再明显。

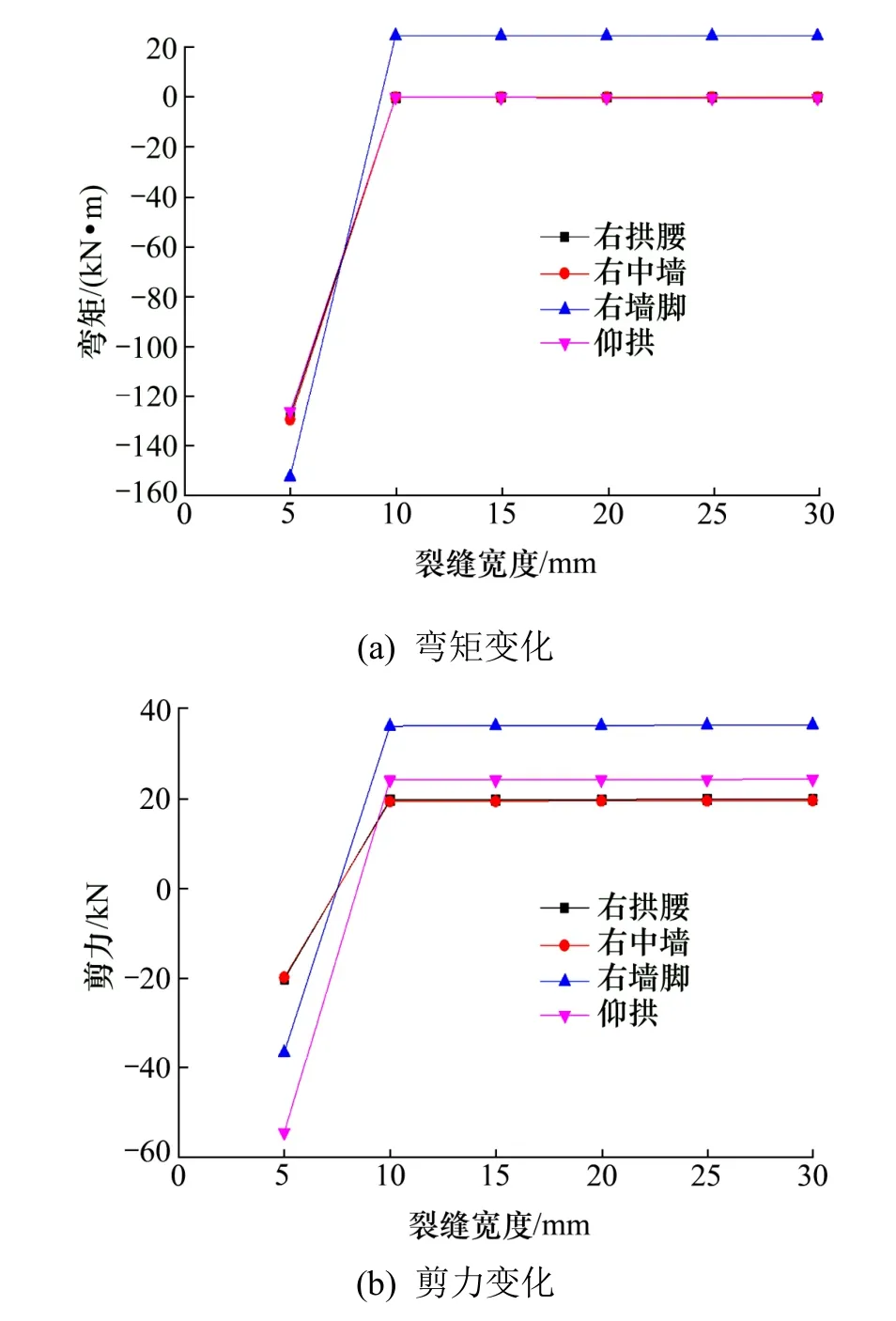
图20 衬砌典型位置处弯矩和剪力随中墙裂缝宽度增加的变化情况Fig.20 Variation of bending moment and shear at the characteristic position of lining with the increasing of crack width at sidewall

从图20 中可以看出来，衬砌弯矩随着裂缝宽度的增大发生变化。当中墙处裂缝宽度由5 mm 扩张到10 mm 时，对单元受力结构影响最明显。由于裂缝宽度的扩张，影响了结构弯矩的重分布，致使拱腰、中墙、墙脚、仰拱等部位弯矩减小。当裂缝扩张到10 mm 之后，随着裂缝的再次扩张，对结构弯矩的影响表现不明显。

随着裂缝宽度的增加，在衬砌范围内，剪力发生了变化。当中墙处裂缝宽度由5 mm 扩张到10 mm 时，对单元受力结构影响最明显，由于裂缝宽度的扩张，影响了结构剪力的重分布，致使拱腰、中墙、墙脚、仰拱等部位的剪力先减小到零而后增加到22 kN。当裂缝扩张到10 mm 之后，结构剪力随着裂缝的再次扩张，其影响不明显。

从图21 中可以看，当裂缝位于墙脚处时，衬砌弯矩随着裂缝的横向扩张变化不明显。当裂缝仅发生在墙脚时，在衬砌范围内，剪力随着裂缝宽度的增加发生了变化。当拱顶裂缝宽度由5 mm 扩张到10 mm 时，对单元受力结构影响最明显。由于裂缝宽度的扩张，影响了结构剪力发生重分布，致使拱腰、中墙、墙脚、仰拱等部位弯矩减小。当裂缝扩张到10 mm 之后，结构剪力随着裂缝宽度的增加，改变不明显。

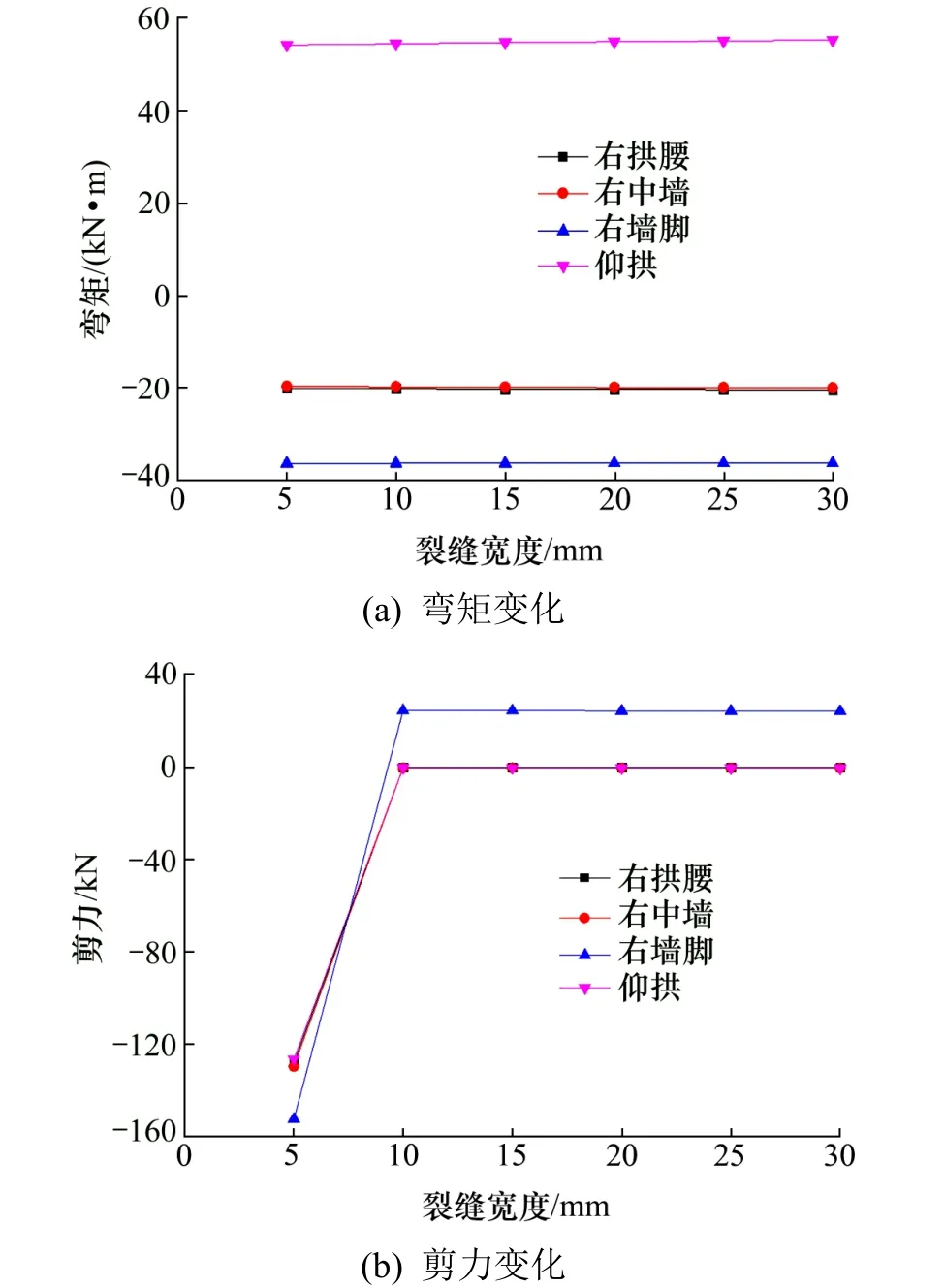
图21 衬砌典型位置处弯矩随墙脚裂缝宽度增加的变化情况Fig.21 Variation of bending moment and shear at the characteristic position of lining with the increasing of crack width at arch foot

3.3 结果分析

通过对裂缝出现的部位与裂缝深度和宽度的不同，对衬砌结构的受力特性影响进行了分析。表明：隧道衬砌发生裂缝病害时，结构承载能力和结构应力会受到裂缝深度、裂缝宽度和裂缝位置的影响。因此，在分析衬砌裂缝对衬砌结构受力性能的影响时，应该从衬砌裂缝发生的部位、裂缝深度和裂缝宽度等因素下，考虑不同隧道截面处裂缝的影

响。裂缝深度相同时，结构的受力和弯矩随着裂缝宽度的增加，也发生相应的变化。当裂缝宽度由5 mm 扩展到10 mm 的过程中，对结构弯矩、剪力的影响最为敏感。裂缝宽度的变化过程中，中墙和拱顶部位裂缝扩展时，对结构弯矩、剪力的影响大致相同；在拱肩和墙角处呈现不同现象，对剪力的影响大，对弯矩的影响很小。

4 结论

基于结构−荷载模型，采用有限元分析软件，考虑衬砌裂缝发生的部位、裂缝深度和裂缝宽度等因素，研究了衬砌裂缝对隧道衬砌结构受力的影响，得到的结论为：

1) 当裂缝发生在拱顶位置时，随着裂缝深度增加，隧道衬砌弯矩始终呈对称分布，仰拱部位出现最大正弯矩值，中墙位置出现最大负弯矩值；剪力呈现出反对称分布，左墙脚出现最大负剪力，右墙脚出现最大正剪力。当裂缝发生在拱肩、中墙或墙脚的位置时，随着裂缝深度的增加，衬砌结构弯矩由近似对称向非对称变化，剪力始终呈现非对称分布。

2) 当裂缝发生在拱顶和中墙时，裂缝深度不变条件下，随着裂缝宽度的增加，其衬砌弯矩和剪力值减小。当裂缝发生在拱肩和墙角位置时，随着裂缝宽度的增加，衬砌结构弯矩变化不明显，剪力值逐渐减小，并反向增大，直至稳定。当裂缝宽度由5 mm扩张到10 mm 时，衬砌结构受力变化最为明显。

3) 结构荷载一定的情况下，裂缝深度越大，缝宽越宽，衬砌结构越容易出现应力集中现象，结构可能发生失稳，甚至破坏。

4) 裂缝出现的位置对结构受力的影响也不相同，拱顶出现裂缝衬砌受力表现最为敏感，因而所带来的危险更为严重。

本研究仅对单一部位出现开裂，该裂缝宽度和深度对衬砌结构受力影响进行了模拟分析，后续研究采用该方法对两处及多处部位同时出现裂缝，以及该裂缝的扩张对衬砌结构的弯矩和受力性能进行定量分析。