带墙脚装置的框架-摇摆墙结构模型研究
2021-12-20姚诞圣
姚诞圣,陈 跃
(1.同济大学 土木工程学院,上海 200092;2.宁波工程学院 浙江省土木工程产业化建设工程技术研究中心,浙江 宁波 315211)
0 引 言
传统抗震结构如剪力墙结构和抗弯矩框架已在抗震领域得到广泛研究和应用[1-4],当发生大震时,这些结构材料的非线性变形是难以避免的[56]。为减少结构的损坏,摇摆这一概念被引入地震工程中[7],并提出了自复位结构[8-11]。框架-摇摆墙结构是自复位结构的一种(图1)。大量实验表明摇摆墙在遭遇大震后,墙体的主体部分完整程度较高,但墙脚处易发生破坏[12-13]。而框架-剪力墙结构在大震后,剪力墙墙脚处也会发生类似的破坏。

图1 摇摆墙Fig.1 Rocking wall
为减小这种破坏,多种加固剪力墙墙脚的方法,其中常见的一种方法就是为剪力墙增设墙脚装置[14-16]。PRETI等提出在墙脚部位使用高强度纤维钢筋混凝土来加强和保护墙脚处,并对带有这种墙脚的剪力墙进行了足尺拟静力试验[16];刘其舟等针对剪力墙结构设计一种可更换墙脚装置,给出了该装置的工作机理和设计方法[17];吕西林等提出了一种由叠层橡胶垫和软钢板组成的可更换墙脚装置[15,18];毛苑君等对可更换墙脚的剪力墙装置进行了拟静力试验[19]。这些墙脚装置在试验和模拟中均表现出良好的性能,表明为墙体增设墙脚装置是增加结构韧性的有效方法。但摇摆墙的工作机理与传统剪力墙不同,在地震作用下,墙体会发生摇摆而导致墙脚与地面脱离。上述剪力墙墙脚装置都具备较大抗拉刚度,从而影响到摇摆墙的工作机理,导致其摇摆无法正常进行。此外摇摆墙墙脚装置对结构内力和变形的影响以及墙脚装置的设计要点都亟待研究。
为研究带墙脚装置的框架-摇摆墙结构的抗震性能及分析墙脚装置设计的要点,提出一种分布参数模型以分析该结构在地震荷载下的性能,给出了在倒三角形分布荷载作用下该模型的边界条件和通解,通过OpenSees验证模型的有效性,通过对墙体和墙脚装置进行了参数分析,以期为墙脚装置的设计提供帮助。
1 可更换墙脚构造
为摇摆墙加设墙脚装置可以分担墙脚处竖向荷载,使其在大震下不发生破坏。墙脚装置应能在设计地震下提供足够的恢复力以减少该装置内侧混凝土承载力需求。由于实际工程中结构参数并不恒定,墙脚装置的刚度需求变化幅度较大,其构造应能较为便利的调整自身刚度。
如图2所示,可更换墙脚装置由约束装置和内部碟形弹簧组构成,其中约束装置由芯棒、底座及上下约束钢板组成。芯棒、底座分别与上下约束钢板焊接。碟簧组串入约束装置,且仅承受压力。该墙脚装置被设计为能够在设计地震下为自复位预制混凝土剪力墙提供恢复力,有利于减少结构的残余变形及减轻墙脚的破坏程度。底座可以被打开以在震后更换碟簧组及芯棒。内部芯棒刚度较大,在工作过程中变形轻微。芯棒侧面需进行润滑或采取构造措施以降低碟簧组与芯棒之间的摩擦。下约束板和地面刚接,在固定墙脚装置的同时,起到约束墙体底部的侧向滑动的作用。

图2 可更换墙脚装置Fig.2 Replaceable toe device
可更换墙脚装置刚度由内部碟形弹簧总刚度决定。碟形弹簧组刚度的理论公式如下
F=mF1=Ns
(1)
f=nf1
(2)
H=n[H0+(m-1)t]
(3)
式中F1为单片碟簧承载力;F为组合碟簧承载力;f1为单碟簧变形;f为组合碟簧变形;n为每组组合碟簧单碟簧数量。当仅考虑叠加表面之间的摩擦时,复合碟形弹簧的承载力可计算如下
(4)
其中FR为碟形弹簧组合的承载力;fM为摩擦系数。
2 带墙脚装置的框架-摇摆墙结构分布参数模型
文中提出了一种带墙脚装置框架-摇摆墙结构的分布参数模型,通过与OpenSees模型进行对比验证了模型的有效性,对墙脚装置进行了参数分析(图3),由摇摆墙部分和框架部分组成。摇摆墙由混凝土墙体、耗能装置、预应力钢筋和墙脚装置组成。模型在水平方向上承受倒三角形线荷载。摇摆壁的刚度为EI,框架的角刚度为K。结构高度为h。墙脚装置的长度为Lfw,刚度为Kfw。当Lfw=Kfw=0时,该结构为不带墙脚装置的框架-摇摆墙结构。摇摆墙中常见的耗能装置是位移相关型阻尼器,如摩擦阻尼器和金属阻尼器[21-23],这些阻尼器的刚度模型大多可以简化为多折线型。
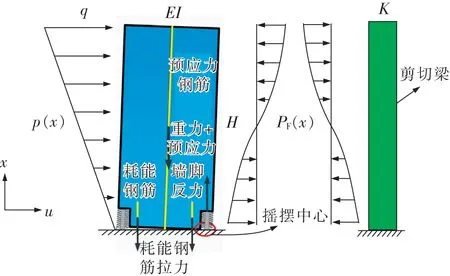
图3 带墙脚装置的框架-摇摆墙结构分布参数模型Fig.3 Parameter model for the rocking wall-frame structures with toe devices
2.1 分布参数模型假定
模型的基本假设如下
1)摇摆墙简化为弯曲梁,框架简化为剪切梁。
2)耗能软钢的刚度简化为双折线模型进行计算,为了与OpenSees的钢筋模型保持一致,假定屈服后的刚度为屈服前的1.2%[24]。
3)预应力钢筋未屈服,且其作用点为摇摆墙的中心,合力的方向始终垂直于地面向下。
4)框架和摇摆墙沿高度(x方向)通过刚性链杆连接,即框架和摇摆墙在水平方向上具有相同的变形。
5)墙脚装置被简化为刚度恒定的弹簧,且其恢复力作用点为其顶部中心线处。
2.2 分布参数模型公式推导
设外荷载为倒三角分布,根据弯曲梁力的平衡关系并引入无量纲系数λ和ξ后可得
(5)
其中q为倒三角分布线荷载的顶部最大荷载集度,即p=qξ。λ代表墙体相对于框架的相对刚度,而ξ则为结构归一化高度(式(6)和(7))。
(6)
(7)
忽略4次项,式(5)通解可被表示为
(8)
摇摆过程可分为3个阶段,即摇摆开始前、摇摆开始但耗能钢筋未屈服和耗能钢筋屈服后。其边界条件也会随着特定的阶段而变化。
在3个阶段中都有:①底部位移为0;②顶部弯矩为0;③顶部合剪力为0。根据分布参数模型的具体阶段,其中一个边界条件需要被分为如下情况讨论。
2.2.1 第1阶段(摇摆开始之前)
此时边界条件为:底部转角为0
将该边界条件代入原方程中,解得
C1=-B=
(9)
(10)
2.2.2 第2和第3阶段(摇摆开始后)
在摇摆开始后,带墙脚装置的摇摆墙底部受力如图4所示,墙体围绕着结构底部墙脚装置内侧进行摇摆。该边界条件为

图4 摇摆墙截面受力分析Fig.4 Force analysis of the cross-section of the rocking wall
底部合弯矩为0
假设两侧耗能钢筋同时屈服,且其变形量与计算位移角下墙体底部中线处的变形相同,则有
(11)
式中Mvar为底部弯矩与转角相关部分系数;Mcons为底部弯矩与转角无关系数。由此可求得式(5)的解为
C1=
(12)
(13)
A=
(14)
B=
(15)
对第2阶段(摇摆开始且耗能钢筋未屈服)和第3阶段(耗能钢筋屈服后),Mvar和Mcons取值如下
(16)
(17)
(18)
(19)
式中δey为耗能软钢屈服点;Kes为耗能软钢屈服前刚度;Kesy为耗能软钢屈服后刚度;fp0为初始预拉力;Kps为预应力钢筋线刚度。
2.3 分布参数模型阶段划分
为了确定摇摆是否已经开始,可以求解第2阶段对应解的零点并表示如下
(20)
若满足该条件,则说明摇摆还未开始,模型处于第1阶段。反之,则说明摇摆已经开始,模型处于第2或第3阶段。
第2和第3阶段则可以根据式(21)进行判断
(21)
若满足该条件,则模型处于第2阶段。反之,则处于第3阶段。
2.4 分布参数模型验证
为验证分布参数模型的有效性,对一带墙脚装置的5层框架-摇摆墙结构分别使用有限元软件OpenSees以及该分布参数模型进行建模,对比2个模型得到的变形、弯矩及剪力。该案例结构的样式如图5所示,剪力墙截面为2 400 mm×300 mm;框架柱截面为0.6 m×0.6 m。层高3 m,共5层。
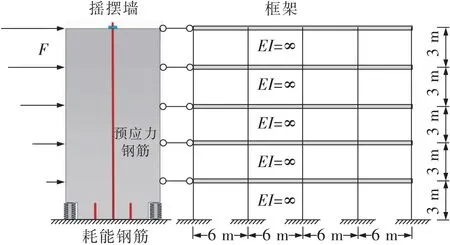
图5 5层框架-摇摆墙结构OpenSees模型Fig.5 OpenSees model of the five-story rocking wall frame structure
在OpenSees模型中,摇摆墙底部的塑性铰采用ForceBeamcolumn单元进行建模,上部墙体采用ElasticBeamcolumn单元进行简化。ForceBeamcolumn单元对应截面的保护层厚度为20 mm,约束混凝土区域定义在两侧的保护层内。预应力钢筋和耗能钢筋均采用Truss单元Steel02材料进行模拟。墙脚装置采用Truss单元并使用Elastic-No Tension(ENT)材料进行模拟。ENT材料仅具备抗压强度而无抗拉强度。
为了模拟地震荷载,作用在Opensees模型上的力是离散的,并且满足
(22)
式中Fci为作用在第i层上的集中力;n为楼层总数。
图6给出了该模型在3个阶段下位移和内力沿高度变化的趋势,蓝色星形代表OpenSees结果,红色菱形线代表分布参数模型未调整前的内力,墨绿色菱形线代表分布参数模型调整后的内力。需要注意的是,分布参数模型提供连续值,而OpenSees模型只提供每个节点上的值。由于作用在OpenSees模型上的力是离散的,OpenSees模型提供的剪力在每个单元中都是恒定的。因此,应通过分布参数模型将各节点剪力与对应楼层处剪力进行比较。

图6 分布参数模型及OpenSees模型变形和内力对比Fig.6 Displacement,moment,and shear of the rocking wall via the distributed parameter model and the OpenSees model
分布参数模型高估了弯矩和剪力,尤其是在第2和第3阶段,这可能是因为未考虑倾覆效应。PAN等将部分顶部荷载在分布参数模型中集中施加在顶部,然后进行叠加以模拟倾覆效应的影响[25]。由于摇摆是分阶段进行的,叠加原理对该分布参数模型并不适用。为了使模型更精确,取出OpenSees模型中顶部集中荷载的一半,并将荷载的剩余部分直接转换为倒三角形荷载。由于顶部集中荷载在第1阶段中由框架承担,第2和第3阶段中仅由墙体承担少量荷载,故该荷载对墙体内力的影响可以忽略,而调整后的内力结果与叠加的效果类似,但位移结果将产生明显误差,因此在位移计算中不进行调整。如果采用这种调整方法,OpenSees模型和PM的内力结果将非常接近,最大值的误差小于9.3%。
2.5 参数分析
为研究墙脚装置的设计要点,规定了2个无量纲参数如下
rlf=lfw/Lw
(23)
rKf=
(24)
式中rlf为墙脚装置的相对长度;rkf为墙脚装置的相对刚度,对应于耗能软钢屈服时墙脚装置提供的弯矩与总弯矩的比例,分析了参数rlf,rkf和λ对结构和墙脚装置性能的影响。
2.5.1 摇摆墙和墙脚装置对结构变形的影响
λ对结构变形的影响如图7所示。为了更好地观察结构的位移曲线,图7中的所有位移都通过顶点位移进行了归一化。在模型的第1阶段,较低的λ将使结构的位移形状偏离剪切型。在第2和第3阶段,尽管结构受力已经较大,摇摆墙仍能调整位移形状以使其更均匀。
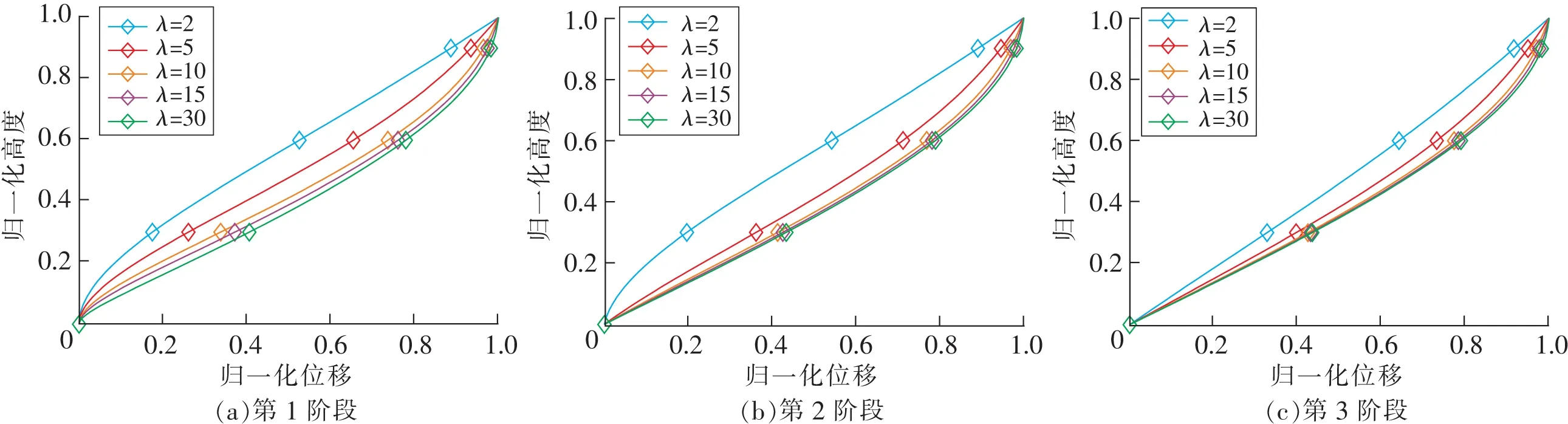
图7 墙体刚度对结构变形的影响Fig.7 Influence of the relative stiffness of the wall on structure displacement
如图8所示,与λ相比,墙脚装置对结构位变形的影响不大。当rlf,rkf分别从0.05增加到0.25和0.01增加到0.3时,结构变形几乎不变。在设计带墙脚装置的摇摆墙时,可以忽略其对结构变形影响而更注意墙体的刚度。

图8 墙脚装置参数对结构变形的影响Fig.8 Influence of the parameters of the toe devices on the displacement of the structure
2.5.2 墙脚装置对墙脚装置性能的影响
墙脚装置可以分担混凝土的部分竖向荷载,以保护混凝土免受损坏,而墙脚装置恢复力在总竖向荷载中所占的比例能有效反应墙脚装置的保护能力。在摇摆开始的节点墙脚装置不提供恢复力,混凝土承担主要荷载,故应注意该节点对应的荷载集度受墙脚装置的影响。
图9给出了rlf和rkf对墙脚装置恢复力占比的影响。rlf对摇摆起始点有很大的影响。随着rlf的增加,摇摆开始所需的载荷减小在摇摆开始后的小载荷范围内,墙脚装置恢复力占比增加。当载荷继续增加超过临界点时,该比例随载荷的增加而显著降低。随着rkf增加,该比例单调增长且不影响摇摆开始所需的荷载。
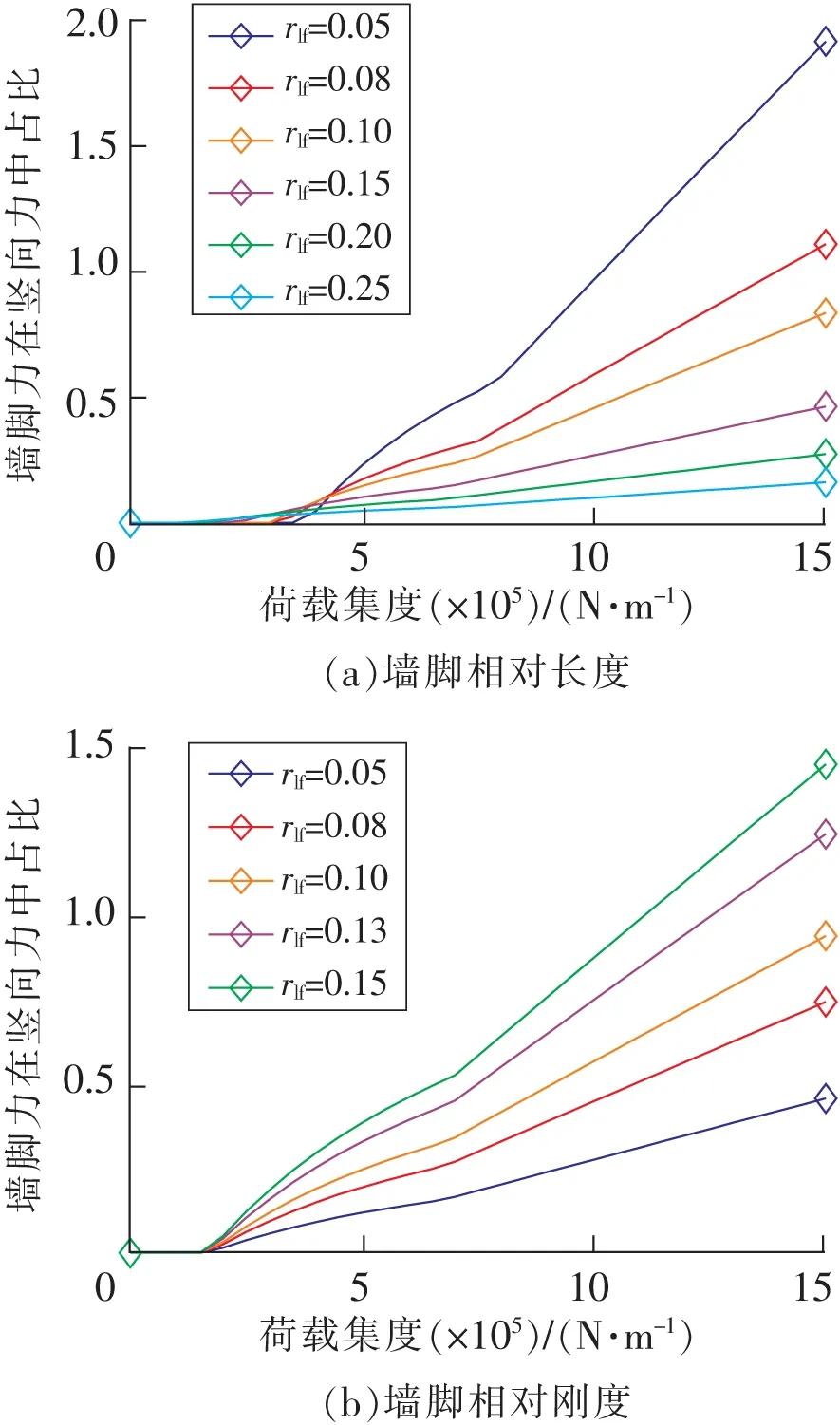
图9 墙脚装置参数对其恢复力占比的影响Fig.9 Influence of the parameters of the toe devices on the proportion of the reaction in the vertical loads
2.5.3 墙脚装置相对长度和相对刚度对性能的综合影响
在相同载荷下,如果摇摆已经开始,则结构位移角将随着rlf的增加和rkf降低而增加。荷载越大,这一现象就越明显。且随着rlf的增大,rkf对结构位移角的影响越来越小(图10)。
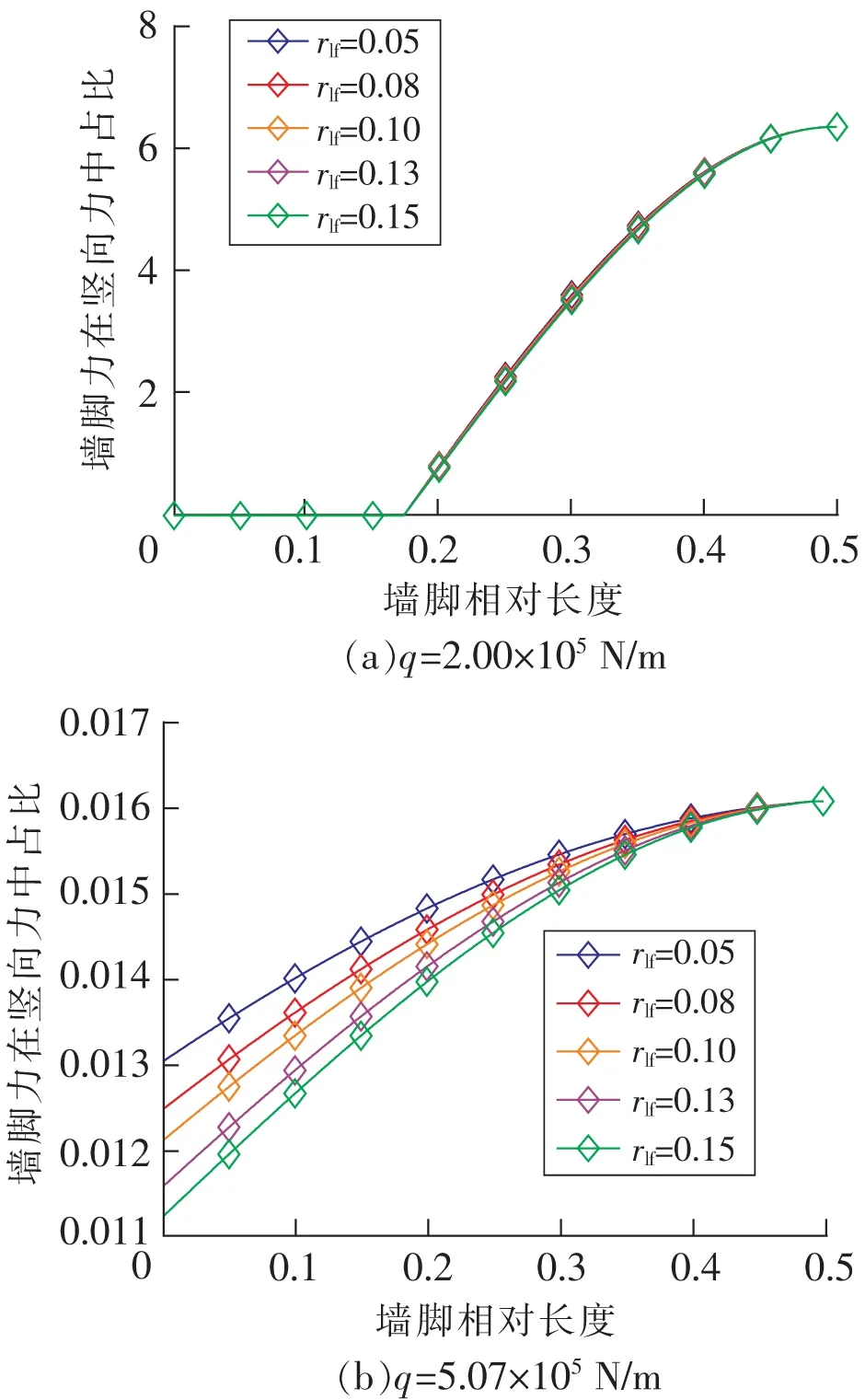
图10 墙脚装置参数对结构位移角的影响Fig.10 Influence of the relative stiffness of the toe devices on the drift angle of the bottom of the wall
rlf和rkf对墙脚装置恢复力占比的影响与荷载的大小有关。当载荷相对较小时,如果rlf较小,摇摆可能还未开始。在这种情况下,随着rkf的增加,墙脚装置恢复力占比增加。但随着rlf和rkf的进一步增加,墙脚装置恢复力占比将先增大到峰值,然后减小。与该峰值对应的rlf不受rkf的影响。当荷载足够大时,无论rlf多小,摇摆都会发生,随着rlf的增加和rkf的降低,墙脚装置恢复力占比将减小(图11)。

图11 墙脚装置参数对其恢复力占比的综合影响Fig.11 Influence of the parameters of the toe devices on the proportion of the reaction in the vertical loads
为了使墙脚装置的恢复力尽可能大,rkf应相对较大。如果在相同的结构变形和相同的相对刚度下,墙脚装置需要提供更大的恢复力,则rlf应尽可能的低。但荷载相对较低时,墙脚装置恢复力占比就较低。在比较多个大小载荷下的模型后,文中建议当rkf在0.05到0.15之间时,rlf应限制在0.1到0.3之间。这样在荷载不大的时候也能使墙脚装置承担一定的荷载从而减小墙体底部混凝土的负荷,另一方面也可以防止墙脚装置提前进入塑性。
3 结 论
1)分布参数模型可以比较准确地反应带墙脚装置的框架-摇摆墙结构的内力和变形,其误差在案例中小于9.3%。
2)摇摆墙在摇摆初期对结构变形影响较明显,在外荷载较大时也能有效调节结构的变形形状,墙脚装置对结构归一化后的变形影响轻微。
3)墙脚装置的相对长度rlf会影响到摇摆开始所需的荷载,而相对刚度rkf则不会影响该荷载。且在相同载荷下摇摆开始后结构位移角将随rlf的增加和rkf降低而增加。
4)rlf和rkf对墙脚装置恢复力占比的影响与摇摆开展的程度有关。为了使墙脚装置在整个摇摆的过程中都能提供较大的恢复力,当rkf在0.05到0.15之间时,rlf宜限制在0.1到0.3之间。
