基于相位相序调整的双向绿波设置方法

2020-02-06张驰

交通科学与工程 2020年4期

张驰

(彦云网络科技(上海)有限公司，上海 201210)

绿波控制能减少城市干道上车辆停车次数和停车时间，满足干线上行驶车辆“一路绿灯”的需求。考虑上、下行2 个方向的绿波控制方式称为双向绿波控制。

交叉口相位相序的设计影响双向绿波带的带宽，国内外已开展了较多有关交叉口相位相序的设计影响双向绿波带带宽的研究及应用。Little[1]等人提出求解最大带宽的混合整数线性规划模型。Messer[2−3]等人在前人的研究基础上，提出了包含左转相位的绿波带宽优化算法，该算法被广泛使用在PASSER II、MAXBAND 等带宽优化软件中。马楠[4]等人在PASSER II、MAXBAND 带宽软件优化算法上，提出了基于相位相序调整的绿波带宽优化模型。唐克双[5]等人提出了MULTIBAND 干线协调控制模型，该模型通过取消绿波带的中心对称约束，增加绿波带位置的约束提高绿波带带宽。常玉林[6]等人提出了一种改进的城市干线双向绿波控制优化设计图解法，可以根据实际的交通需求实现双向不同带宽需求的绿波协调控制，适用于进口不同的放行方式。李硕[7]等人采用相位矩阵的表示方法，对干道信号控制交叉口相位相序的优化进行研究。郑淑鉴[8]等人对基于交通疏解的干道协调控制模型及应用进行了研究，并提出利用上、下行红灯中心点偏差，优化交叉口相位相序方法。李克平[9]等人指出干线协调信号控制中各个交叉口的相位结构，可按照交叉口与双向绿波带中心线交点之间的距离确定，可以提高双向绿波带的带宽。

交叉口相位相序设计方面，由于传统的相位相序设计方法不灵活，国内研究者对双环相位结构(NEMA 相位)[10]进行了研究，相比于传统的相位相序设计方法，可有效提高相位相序设计的灵活性。陈昕[11]等人提出了一种基于绿波带中心线交点的双向绿波控制图解法，通过寻找合理的相位相序设计，使临近交叉口的各个绿波带中心线交点之间的水平间距，尽量为零或交叉口理想间距的整数倍，可提高绿波带的带宽。卢顺达[12−13]等人对非对称方式下的图解法进行了改进设计，使用NEMA 相位来改变交叉口车流的放行顺序，能够增加双向绿波带宽。这些研究成果表明：交叉口不同放行方式下，不同相位相序设计能够提高绿波带的带宽，但因现有的优化模型较为复杂，大都没给出不同放行方式下的相位相序设置方法。针对双向绿波控制中相位相序的调整，需要依靠交通信号调优工程师长期积累的经验对相位相序进行调整。因此，作者拟提出一种提高双向绿波控制中绿波带带宽的相位相序调整方法，结合NENA 相位和图解法，对相位相序进行调整，以达到提高双向绿波控制中绿波带带宽的目的。

1 相位相序调整的原理

对交叉口的绿波带中心线交点、绿波协调控制的绿波带中心线交点和信号协调控制交叉口的中心线进行定义，分析其影响因素，并在时距图(如图1 所示)中表示，提出双向绿波带带宽最大相位相序调整的原理。

图1 绿波带中心线交点Fig.1 The intersection point of the center line of the green wave band

绿波设计的时距图中，交叉口一个信号控制周期内，在上行方向，经绿灯开始时刻、结束时刻2点的中点，以行车速度的倒数为斜率作一条直线；在下行方向，以行车速度的倒数的相反数为斜率，作另一条直线。两条直线的交点为交叉口的绿波带中心线交点。两条直线的交点为该交叉口的绿波带中心线交点(交叉口C的绿波带中心线交点CTP为虚线LC1、LC2的中心线LC12与虚线LC3、LC4的中心线LC34的交点，如图1 所示)。交叉口绿波带中心线交点位置与交叉口位置、绿波带带速和信号控制的相位相序有关。

绿波协调控制的绿波带中心线交点为时距图上、下行方向的绿波带中心线的交点，如图1 所示，以实心圆表示。与绿波协调控制的绿波带中心线交点、交叉口位置和绿波带带速有关。

信号协调控制交叉口的中心线是与交叉口信号协调控制上、下行方向2 条停车线平行的中点线，如图1 所示，以MA、MB、MC、MD、ME、MF、MG线所示。信号协调控制交叉口的中心线与交叉口几何形状有关，交叉口的中心点在交叉口的中心线上。

理想交叉口间距为时距图中2 个相邻绿波协调控制的绿波带中心线交点的水平距离。其计算式为：

式中：V1、V2分别为上、下行方向绿波的行进车速，m/s；C 为公共周期，s。

当两两交叉口的绿波带中心线交点水平之间的距离等于零或等于理想交叉口间距的整数倍，即两两交叉口的绿波带中心线交点水平之间的距离之差与理想交叉口间距的余数之和为最小时，交叉口相位相序对应的双向绿波带的带宽最大，基于此调整交叉口的相位相序。

2 基于相位相序调整的双向绿波设置方法

通过对相位相序影响绿波带带宽的分析，结合时距图，提出提高双向绿波控制中绿波带带宽的相位相序调整方法(指相位顺序的调整)，如图2 所示，具体步骤为：

图2 交叉口间距、车道类型Fig.2 Intersection spacing and lane type

1）确定双向绿波控制中每一交叉口的相位方式，即确定每一交叉口的相位和绿波控制的公共周期C。

2）根据NEMA 相位相序设计标准，确定每一交叉口可能设置的不同相位相序。

3）根据上、下行方向绿波的行进车速和公共周期，按照式(1)，求解绿波控制的理想交叉口间距lTP。

4）确定各交叉口的相位相序。以绿波控制中上行方向的第一个交叉口为基准交叉口，求解除基准交叉口外每一交叉口的不同相位相序对应的绿波带中心线交点与基准交叉口的不同相位相序对应的绿波带中心线交点之间的水平间距与理想交叉口间距余数之和的最小值P，并根据P 确定每一交叉口的最佳相位相序。

将绿波控制的交叉口名称按字母表从字母A顺序依次编号。设交叉口A 为基准交叉口，交叉口A 对应的相位相序为AP,i，相位相序AP,i对应的绿波带中心线交点基准点为ATP,i(i=1,2,3,4,…)，i 为同一交叉口符合要求的相位相序；其他交叉口(交叉口B、C、D、…)对应的相位相序为BP,i、CP,i、DP,i、…，对应的绿波带中心线交点为BTP,i、CTP,i、DTP,i、…。

①根据交叉口A 的相位相序AP,1对应的基准点ATP,1，确定其他交叉口的相位相序。再依次计算其他各交叉口所有满足要求的相位相序对应的中心线交点与基准点ATP,1的水平间距，并与理想交叉口间距lTP取余，如式(2)所示。然后对各交叉口的取余结果相加，得到Min1。

②重复步骤4.1，依次求基准交叉口A 的各个相位相序对应的基准点ATP,i(i=2,3,4,…)和Min2,Min3,Min4,…。

③取Min2,Min3,Min4,…的最小值P，P 对应的各个交叉口的相位相序为绿波控制的最佳相位相序。

5）根据最佳相位相序和图解法，在时距图中调整各交叉口的周期起始时刻，找到上、下行方向的最大绿波带带宽。时距图的上行方向，以行车速度的倒数为斜率作直线一。以直线一为参考，在时距图中，上、下拖动，改变各个交叉口绿灯的起始时刻，使得直线与协调相位绿灯开启时刻相交。下行方向，以行车速度倒数的相反数为斜率作直线二，以同样的方法进行拖动，直到找到上、下行方向最大的绿波带为止。

6）根据时距图得出绿波带带宽、各个交叉口的相位差和最终信号控制方案。

3 算例分析及仿真试验

3.1 双向绿波设置方法算例分析

以某市东西向干道7 个连续的交叉口为例，基于相位相序调整的双向绿波设置方法，分析该方法提高双向绿波带带宽的效果。各交叉口的间距及车道类型如图2 所示。除交叉口F 为T 形交叉口外，其余均为十字交叉口。规定西向东方向为绿波控制的上行方向，东向西方向为绿波控制的下行方向。

根据交叉口类型、渠化状况，以及不同时段的不同交通流量确定信号控制的相位方式，并计算制定各个交叉口的信号配时方案，将最大周期的交叉口作为关键交叉口，周期作为公共周期，其他交叉口以该交叉口为参考对各个相位的显示时间进行调整。本算例研究某一时段对应的一种交通信号配时方案。研究7 个交叉口的间距、交叉口宽度，时段中路段的平均车速和协调方向的绿灯时长等数据见表1。

按式(1)求理想交叉口间距lTP=625 m，按照基于相位相序调整的双向绿波设置方法中的步骤4 确定各交叉口相位相序，使两两交叉口的绿波带中心线交点水平间距与理想交叉口的间距的余数之和最小，得到最佳相位相序。各交叉口调整前、后的相位相序，如图3 所示。

表1 绘制时距图的基础数据Table 1 Basic data for plotting time-distance maps

以各交叉口调整前、后的相位相序为基础，在时距图中调整各交叉口的周期起始时刻，得到上、下行方向最大绿波带带宽，如图4 所示；确定各交叉口的相位差，见表2；得到最终信号控制方案。

从图4(a)中可以看出，相位相序必须进行调整，否则双向绿波较难实施。将上行方向作为主要协调方向，实施绿波协调方案。上行方向绿波带带宽为40%，绿波带带宽可达度为90.9%；下行方向绿波带带宽为25%(绿波带在交叉口C 断开)，G、F、E、D 4 个交叉口的绿波带带宽仅为50%。采用基于相位相序调整的双向绿波设置方法对相位相序调整后。通过图解法，可知双向绿波带的带宽增加。从图4(b)中可知，上行方向绿波带带宽为44%，绿波带带宽可达度为100%；下行方向绿波带带宽为30%，绿波带带宽可达度为76.9%。

3.2 VISSIM 仿真试验

图3 调整前后相位相序对比Fig.3 Phase sequence comparison before and after adjustment

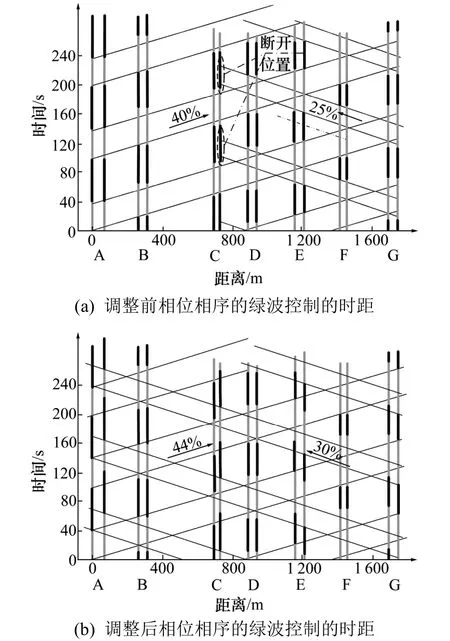
图4 绿波带带宽对比效果Fig.4 Comparison of green bandwidth

对相位相序调整前、后的双向绿波方案进行VISSIM 仿真试验，输出平均行程时间、平均延误、平均停车次数等仿真结果，对比相位相序调整前、后的实施效果。仿真的目的在于获取干线直行车的行程时间、延误时间、停车次数等参数，该仿真试验仅对直行方向的交通流及对应的相位相序调整前、后的绿波信号控制方案进行仿真试验，并对仿真结果进行对比分析。将图3 作为底图，导入仿真软件，建立路网，对仿真参数、信号控制方案进行设置，输入车辆。并将相位差见表2，红灯、绿灯结束时刻见表3，输入VISSIM 仿真程序。

表2 相位相序调整前后绿波控制的相位差Table 2 Phase difference of green wave control before and after phase sequence adjustment

表3 协调方向信号控制方案Table 3 Signal control scheme for coordinated direction

上、下行方向的第一个交叉口进口和最后一个交叉口出口的位置，设置2 组行程时间检测器，分别对7 个交叉口相位相序调整前、后的绿波控制方案进行仿真试验。通过干道车辆的平均行程时间、平均延误、平均停车次数仿真结果见表3。由表3可知，上行方向车辆平均延误时间由30.7 s 降低为28.7 s，平均停车次数由0.88 次降低为0.8 次；下行方向车辆平均延误由142.9 s 降低为29.9 s，平均停车次数由3.59 次降低为0.96 次。