考虑剪力滞效应和附加轴力的箱梁自振分析

李梦瑶

(昆明理工大学 建筑工程学院，云南 昆明 650500)

箱梁因自重轻、施工方便等优点被广泛应用于桥梁建设中。因为箱梁截面非实心，所以箱梁截面的应力分布较复杂，剪力滞效应尤为突出。当箱梁承受竖向荷载产生竖向挠曲变形时，上、下翼缘板产生剪切变形，而腹板在上、下翼缘板之间传递剪力流过程中，由于应力集中，导致翼缘板纵向位移，沿桥宽方向产生不均匀的变化，这种现象叫剪力滞效应。所有箱梁结构的动力分析都要求对其剪力滞效应进行分析，因此，许多学者对此进行了大量的研究。吴有俊等[1−2]人基于实际变形下中性轴和形心轴的重合，根据能量变分原理进行推导，得到了考虑剪力滞效应的简支梁强迫振动微分方程及其边界条件。蔺鹏臻等[3−5]人根据简支梁的纵向静力平衡条件进行推导，得出了附加轴力的表达式，并研究了其对剪力滞效应的影响。潘旦光[6]等人采用模态摄动法求解出简支薄壁箱梁自由振动解析解，根据简支梁振动模态提出了模态剪力滞系数的概念，并建立了剪力滞效应与自振频率之间的关系。蔡恒[7]等人根据能量变分原理推导出曲线梁桥的自由振动微分方程，并假设位移场函数为正弦函数，对微分方程近似求解。刘建新[8]等人利用能量变分法推导出简支梁强迫振动方程，建立了微分方程解的差分格式，讨论了差分格式的准确性。甘亚南[9−11]等人根据能量变分法推导出简支曲线梁和连续梁的弯曲振动方程和边界条件，利用Matlab 软件编程求解得到了固有频率。目前，针对桥梁静荷载作用下的剪力滞效应已经获得许多研究成果[12−14]，而且多数桥梁的动力响应中多数考虑了地震作用[15]，但是同时考虑动剪力滞效应和纵向静力平衡的研究鲜见。因此，作者基于能量变分原理，拟在纵向位移函数中增加全截面均匀纵向位移，推导出同时考虑剪力滞效应和纵向静力平衡的简支箱梁自由振动微分方程，并根据假设模态法对微分方程分离参数，利用Matlab 编程求解自振频率，并与初等梁理论、ANSYS 有限元建模和考虑剪力滞效应的计算结果进行对比分析。

1 模型建立

1.1 基本假定

为了便于分析，忽略部分影响较小的因素，并做出假设：①考虑剪力滞效应时，截面中性轴仍然通过截面形心；②不计阻尼的影响，所有材料均处于线弹性状态；③翼板纵向位移沿宽度方向按3 次抛物线分布[16]；④箱梁截面处于对称弯曲状态。

分析的箱梁截面尺寸如图1 所示。在图1 中，b1,b2,b3,b4分别为顶板宽度、悬臂板宽度、底板宽度、腹板高度；h1,h2,h3,h4分别为顶板厚度、悬臂板厚度、底板厚度、腹板厚度；坐标轴采用直角坐标轴，x轴为纵向，y 轴为横向，z 轴为竖向。

1.2 振动微分方程及边界条件

当i=1 时，表示顶板；当i=2 时，表示悬臂板；当i=3 时，表示底板；当i=4 时，表示腹板。箱梁的纵向位移函数为：

式中： Ui( x , y , z , t )为箱梁的纵向位移函数；Zi为各个板到形心的距离；w 为竖向挠度；为剪力滞效应引起的附加纵向位移； fi( y , z )为u(x)的分布函数。

图1 截面尺寸Fig.1 Section size chart

考虑到简支梁截面纵向静力平衡，由于中性轴与形心轴偏离产生轴力，因此，用附加轴力来进行平衡，将附加轴力引起的纵向位移均匀分布在全截面上。附加轴力的作用下，箱梁的纵向位移函数为：

其中，

式中：ξ 为由轴力引起的纵向位移；y 为箱梁截面待求点的y 坐标。

正应变：

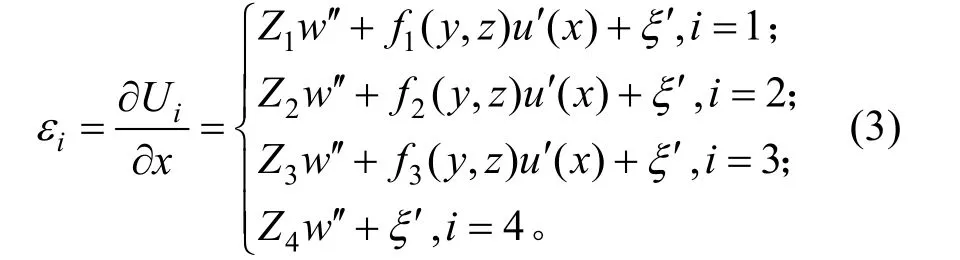
切应变：

根据材料力学中轴力的定义，可得：

式中：E 为弹性模量；A 为箱梁截面的面积。

由于截面中性轴通过截面形心，则截面对形心轴 的 静 矩 为 0，可 得明 显因此，附加轴力为：

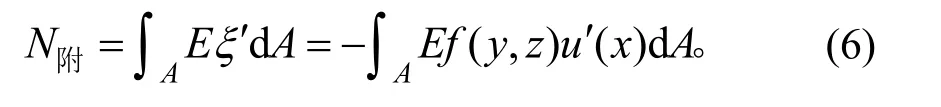
则：

其中，式(7)对y 积分，可得：

式中：A1为顶板的横截面积；A2为悬臂板的横截面积；A3为底板的横截面积。

顶板应变为：

同理可得，悬臂板应变能为：

底板应变能为：

腹板应变能：

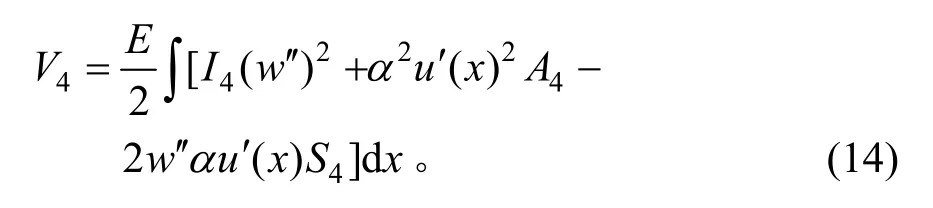
箱梁的动能(仅考虑竖向振动)：

式中：m(x,t)为单位长度的质量。

外荷载所做的功为：

式中：P 为外荷载。

箱梁应变能：

根据哈密顿原理，可知：

式中：δ 为变分符号。

边界条件为：

1.3 振动方程求解

由方程(19)可得：

将(22)，(23)代入(20)，

因研究箱梁的自振分析，则P=0。

令：

式中：ω0为振幅；N 为振型阶数；l 为跨长；ωN为固有角频率；t 为时间；θ 为初相角。

要使式(25)恒等于0，只需令

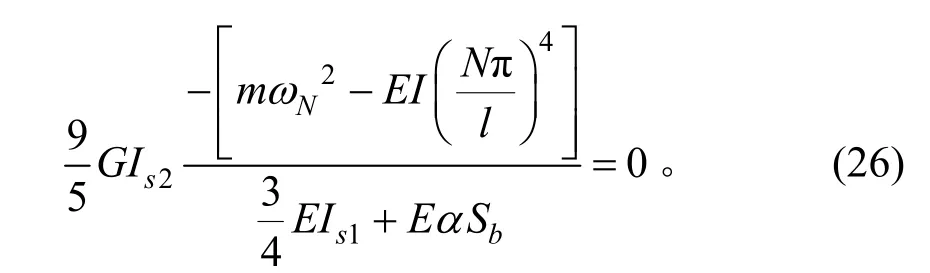
2 算例及结果

某混凝土简支箱形截面梁如图1 所示，其尺寸参数及材料参数为：泊松比为 0.3，弹性模量E=3.5×1010Pa，b1=3 m，b2=3 m，b3=3 m，b4=3 m，h1=0.3 m，h2=0.3 m，h3=0.3 m，h4=0.3 m，密度为2 500 kg/m3。采用ANSYS 有限元软件和Matlab 程序，对不同跨宽比的简支箱梁自振频率进行计算，并与初等梁理论和考虑剪力滞效应变分法的计算结果进行比较，见表1。

由表1 可知，考虑剪滞和轴力的计算结果，与初等梁理论和考虑剪力滞效应的相比，更接近有限元的。跨宽比为3.33 时，振型阶数从一阶到四阶，采用推算方法，计算出自振频率分别为20.170,72.106,145.115,236.248 Hz，均小于初等梁理论和考虑剪力滞效应的结果。表明：考虑剪力滞效应和附加轴力修正的解析解，能够与ANSYS 有限元解吻合。ANSYS 有限元建模过程中，采用BEAM188单元和自底向上的建模方式，约束条件为简支约束，进行模态分析。

根据不同跨宽比的箱梁结果见表2。由表2 可知，附加轴力对自振频率计算精度的影响，跨宽比的增大，附加轴力对自振频率的影响略微变大，但稳定在10%左右。当假设简支梁变形时，中性轴与形心轴位置一致，而实际变形过程中，轴力会对结构的振动产生影响[17]，中性轴与形心轴的位置会产生一定偏移，从而产生了附加轴力。附加轴力会使简支箱梁的相对刚度减小，从而导致结构的自振频率降低，进而使得简支箱梁的自振频率降低。附加轴力对自振频率计算精度的影响已经超过了工程精度的容许值，故求解箱梁自振频率过程中，对附加轴力的考虑是必要的。

表1 各计算方法的自振频率(单位：Hz)Table 1 Frequency comparison of natural vibration (unit: Hz)

通过对不同振型阶数考虑剪力滞效应、初等梁理论、推算方法与有限元建模所得的自振频率进行比值分析。令有限元结果为1，各计算结果如图2所示。从图2 可以看出，当振型阶数一定时，这3种方法随着跨宽比的增加，与有限元模拟结果逐渐接近。当跨宽比为1.67 时，本计算方法与其他两种方法相比，最为接近有限元的结果。当跨宽比为5时，3 种方法与有限元结果均相近。当振型阶数从一阶到四阶时，3 种方法与有限元的计算结果的比值均大，但推算计算方法所得结果相比于其他2 种方法与有限元结果最为接近。由于简支箱梁的剪力滞效应程度受到跨宽比的影响，当跨宽比越小，剪力滞效应越严重，减小了结构的相对刚度，因此，对简支箱梁的自振频率降低程度越大。

表2 附加轴力的影响Table 2 Effect of the additional axial force

图2 自振频率的比值Fig.2 Ratio of natural frequency

3 结论

通过对简支箱梁纵向静力平衡状态下的剪力滞效应分析，得出的结论为：

1) 推算的结果与ANSYS 有限元的较为接近，精度能够满足工程需求，具有一定实用性。

2) 考虑剪力滞效应的自振频率，相比于初等梁理论偏小，是因为剪力滞效应减小了箱梁的相对刚度，使得简支箱梁的自振频率降低，且结构随着跨宽比的减小，剪力滞效应越明显。

3) 附加轴力会造成箱梁相对刚度的减小和自振频率的降低。