纵振型低频压电水听器的等效电路及有限元分析对比研究
2020-01-19徐言哲范桂芬田丰邓皓元胡洪平吕文中
徐言哲,范桂芬,田丰,邓皓元,胡洪平,吕文中
纵振型低频压电水听器的等效电路及有限元分析对比研究
徐言哲,范桂芬,田丰,邓皓元,胡洪平,吕文中
(华中科技大学光学与电子信息学院,湖北武汉 430074)
分别利用等效电路理论与ANSYS有限元仿真对纵振型复合棒式压电水听器的性能参数进行了计算,并将两种结果进行比对分析。对比发现两种分析方法得出的接收灵敏度最大值对应的频率不在同一处并且在数值上存在一定差异,在远离谐振点的较低频段,水听器的接收灵敏度都具有较为平坦的响应。等效电路理论只考虑了一维纵向振动并且将模型完全理想化,而ANSYS有限元分析则考虑了整个结构的纵向横向模态耦合,其建模更接近实际模型,因此ANSYS有限元分析在水听器的仿真优化设计中更符合实际情况,但还需制作实物,用实测结果进行比对。等效电路理论由于物理意义明显,可以为水听器设计和有限元仿真提供理论指导。
等效电路理论;ANSYS有限元仿真;接收灵敏度
0 引言
水声换能器是发射和接收水中声信号的装置,是进行水声学研究的核心设备,其性能好坏直接影响水声设备的性能[1]。水声换能器按其工作状态的不同,可以分为两类:把电磁能转化成声能的一类称为发射器,把声能转化为电磁能的一类称为接收器,也称为水听器[2]。PZT(锆钛酸铅)作为压电陶瓷的一种,其机电耦合系数高、压电常数大、稳定性好,常被用来作为制备压电水听器的换能元件。目前高低频压电水听器的应用都较为广泛,但关于低频纵振型压电水听器,尤其是其在次声波范围的研究和应用较少。
地震、海啸、核爆及火山喷发都会产生次声波,次声波传播时衰减小,传播距离远。水下地震监测,海啸预报、核爆检测及火山喷发等领域都急需低频、宽带、高灵敏度的水听器[3-6]。因此,低频水听器具有极其重要的研究意义。常用的压电水听器结构为纵振复合棒式结构,人们在分析该换能器的工作模式及器件性能时常采用两种方法:一为等效电路法,即将器件等效为理想的阻容元件[7],二为采用有限元建模分析法,国内多位学者进行了研究[8]。但这两种方法由于计算方法和建模的不同,分析结果会有一定的差别。因此本文分别利用等效电路理论和ANSYS有限元仿真,对纵振型复合棒式水听器的性能参数进行理论计算并且进行对比,希望得到一些今后能指导水听器设计计算的有益结论。
1 利用等效电路理论分析纵振复合棒式水听器的性能参数
纵振复合棒式水听器的结构图如图1所示,将纵振复合棒式水听器看作由前盖板、压电晶堆、后盖板3部分组成的机械振动体,忽略了预应力螺栓,由波动理论得出机械振动方程,根据边界条件求解,再由压电方程和机电类比的方法,建立等效电路。

图1 纵振复合棒式水听器结构示意图
等效电路理论的优点是能够直观表达物理意义,结构参数及材料参数能直观体现在数学表达式中[7]。由上述方法,分别得到纵振复合棒式水听器前盖板、压电晶堆、后盖板3部分的等效电路图,再将三者串联,得到最终的等效电路图[2],如图2所示,图中A、B、C三个虚线框中分别为后盖板、压电晶堆、前盖板的分块等效电路。
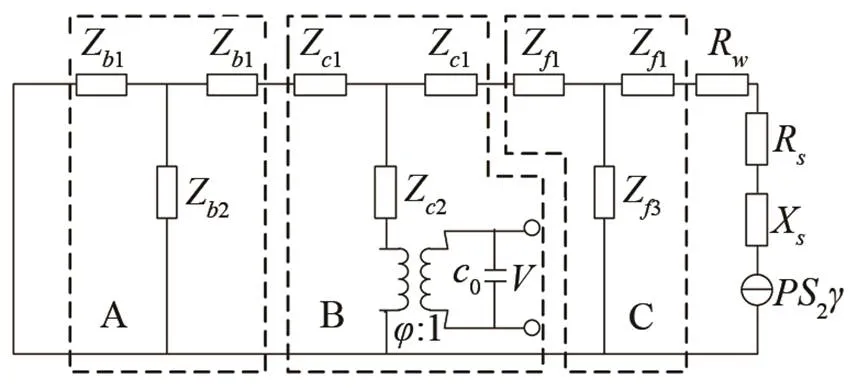
图2 纵振复合棒式水听器的等效电路图
图2中各阻抗表达式如下[2]:
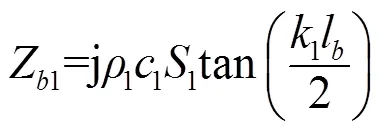




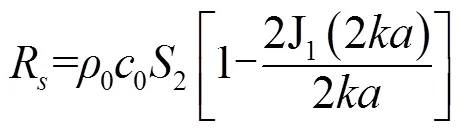


数学表达式(1)~(9)及图2中各参数含义如下:
一阶贝塞尔函数:

一阶斯特鲁夫函数:

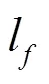

由接收灵敏度定义计算灵敏度:

令:
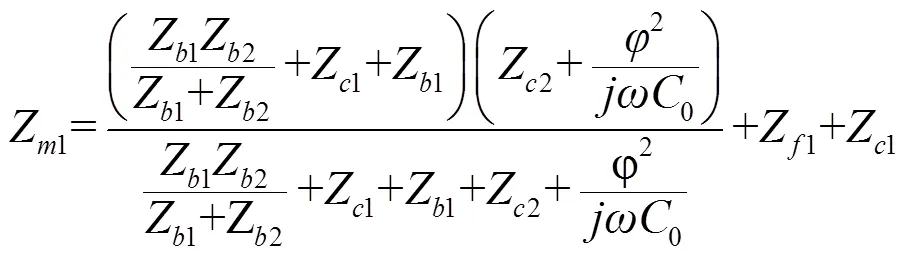


则


再代入式(12)、(13),最后利用式(19)[2]:

代入材料参数和几何尺寸并利用Matlab软件对上述公式进行数值计算,可得到接收灵敏度曲线,如图3所示。
接收灵敏度的最大值约为-170.7 dB,在200~10 800 Hz频段内,接收灵敏度起伏小于等于3 dB。

可得到该模型的导纳曲线,分别取实部虚部得到电导G、电纳B。利用Matlab作图得到电导电纳曲线。如图4所示,本理论模型在有辐射阻抗以及辐射面加载水的情况下,一阶纵振频率大概在20 750 Hz处,最大电导值为0.711 mS。
2 利用ANSYS有限元分析纵振复合棒式水听器的性能参数
ANSYS是目前较为流行的有限元仿真软件,在水听器的设计上,该软件提供了多种单元类型,用于分析结构应力、压电、多物理场耦合等[8]。
ANSYS在处理结构力学线性问题时所依赖的有限元方程如下:


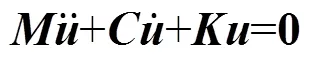
2.1 模态分析
本文利用ANSYS对纵振复合棒式水听器进行模态分析,这里只给出在短路恒压状态和开路恒流状态下的模态分析结果,如图5所示。图5表明了纵振复合棒式水听器的一阶纵向谐振模态振型和一阶纵向反谐振模态振型。
为计算方便,模态分析只建立了二分之一轴对称模型,主要包括前盖板、压电晶堆、后盖板、螺栓4个部分。材质分别选用硬铝、PZT-5H、不锈钢、45#钢。压电晶堆和金属部分赋予的单元类型分别为Plane 42和Plane 13。压电晶堆的材料参数包括介电常数矩阵、刚度矩阵、压电应力常数矩阵及密度。金属部分材料参数包括密度、泊松比和杨氏模量。
由模态分析计算得到,纵振复合棒式水听器一阶纵向谐振频率与一阶纵向反谐振频率分别为20 370.1 Hz和26 810.4 Hz。考虑到工程实际情况,水听器的接收灵敏度最大值应该在反谐振频率附近,如果需要其工作频率在较低频段并且保证接收灵敏度曲线足够平坦,其工作频率的上限保守估计应不大于反谐振频率的1/3。由模态分析得到的一阶纵向反谐振频率,可粗略地将谐响应分析的频率范围定为0~40 000 Hz。

图5 纵振复合棒式水听器一阶纵向谐振模态与一阶纵向反谐振模态
2.2 谐响应分析
建立水中的有限元模型,将六片压电片正极和负极上的所有节点各定义一个耦合部,即电压耦合,使正极或负极上的所有节点电势相同,并在正极与负极上分别施加1 V与0的电压载荷。在前盖板与近水场接触面施加流固耦合界面。水中有限元模型如图6所示。

图6 水听器有限元模型




从图7中可看出接收灵敏度最大值约为-170.5 dB。观察较低频段,曲线一定程度上保持平坦,大约在200~5200 Hz频段内,接收灵敏度起伏小于等于3 dB。
在水中做谐响应分析,可分析出水听器的导纳特性并与等效电路法相比较。在压电晶堆表面正极与负极分别定义电压耦合部,并在正极与负极上分别施加1 V与0的电压载荷,求解后提取正极耦合部序号最低节点上的电荷,在时间后处理中求出电导电纳曲线。在水中的电导电纳曲线如图8所示。此外,还得到水听器在水中的电阻电抗曲线,如图9所示。

图7 基于ANSYS仿真得到的接收灵敏度曲线
从水中的电导电纳曲线(图8)可知,电导最大值约为0.80 mS,此处的频率即为一阶纵向谐振频率,约为20 600 Hz。根据图9,电阻电抗曲线只展现出水听器在水中的一阶反谐振特性,当电阻()取极大值时,该点所处频率对应水听器的接收灵敏度曲线的峰值所处频率,即一阶纵向反谐振频率。观察电抗(),存在一个波峰和一个波谷,波峰对应的频率为,波谷对应的频率为,与水听器接收灵敏度反谐振频率处的-3 dB带宽大致吻合。通过观察与,说明接收灵敏度曲线和阻抗曲线在峰值段趋势差不多。
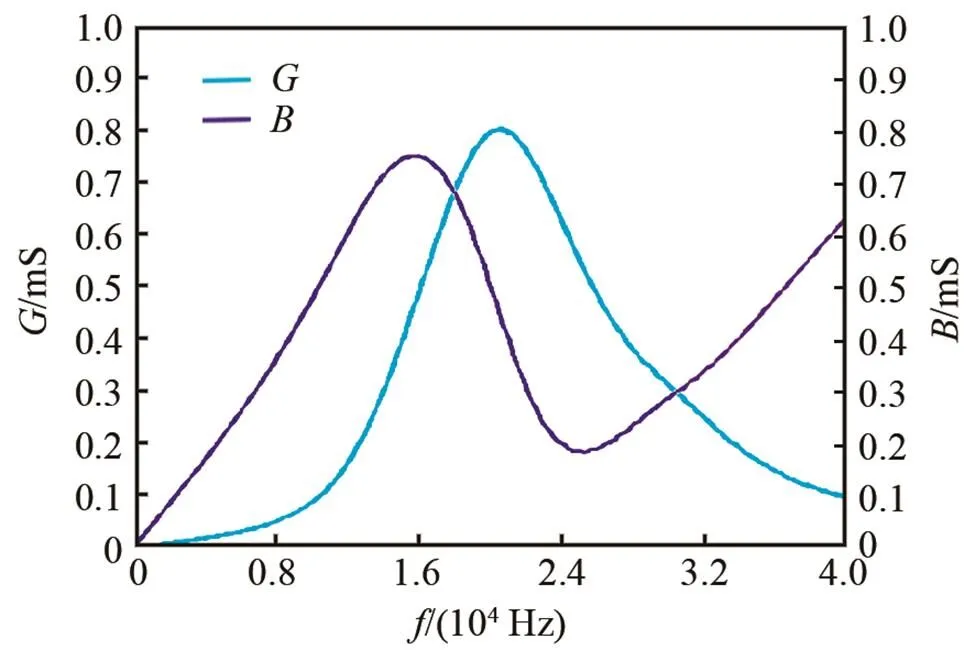
图8 基于ANSYS仿真的换能器在水中的电导、电纳曲线
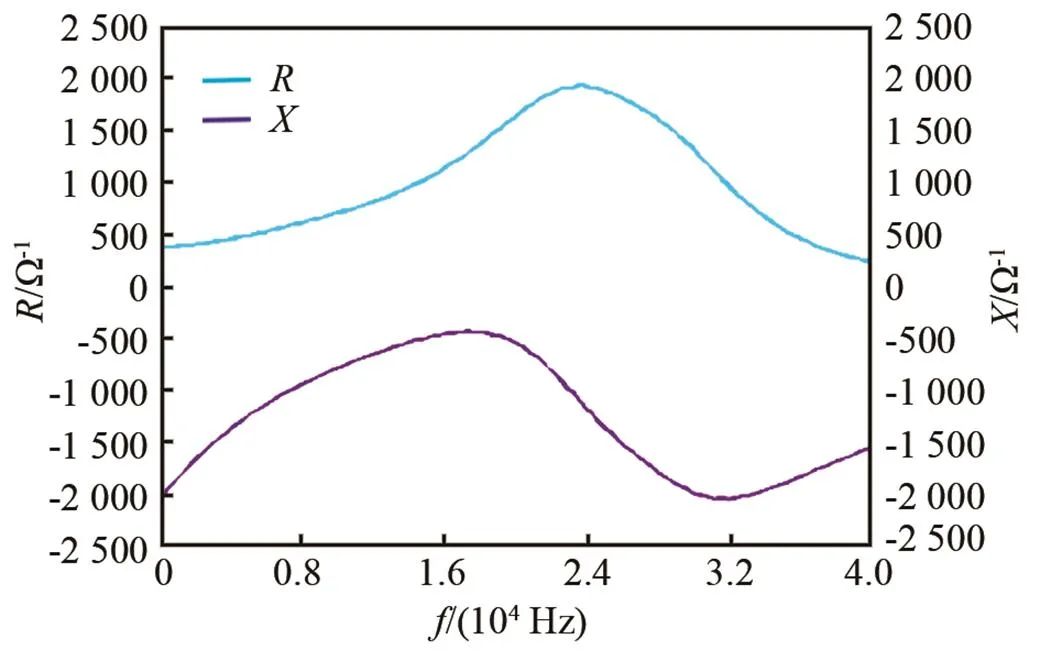
图9 基于ANSYS仿真的换能器在水中的电阻、电抗曲线
3 对比与分析
通过对比接收灵敏度曲线(图3与图7),发现通过等效电路理论与基于ANSYS仿真得到的接收灵敏度最大值分别为-170.7 dB和-170.5 dB,它们对应的频率分别约为23 100 Hz和27 400 Hz,有15.7%的误差。考虑两者带内起伏小于3 dB,分别在200~10 800 Hz与200~5 200 Hz频段内有较为平坦的响应。对比导纳特性(图4与图8),两种方法得到的电导最大值以及所对应的一阶纵向谐振频率存在微小差异,一阶纵向谐振频率分别约为20 750 Hz与20 600 Hz。
造成上述差异的原因可能为:
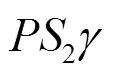
(2) 等效电路理论只考虑水听器一维纵向振动,忽略了其它模态。但通过有限元分析(见图5)可看出,水听器不仅有纵向振动,还包含前盖板、压电晶堆、螺栓的弯曲振动,考虑了整个结构体的纵向横向振动耦合。
(3) 有限元分析中,水听器前盖板与近水场接触面施加了流固耦合界面,而等效电路理论中并未考虑此因素。
(4) 等效电路理论中,水听器的辐射阻抗是理论计算的结果。有限元分析中,谐响应分析中输入的阻尼系数只是经验值,对于实际环境必然存在误差。无论是等效电路理论还是有限元分析,对于水听器的工作环境都进行了理想化。
4 结论
本文通过以上分析,得到以下结论:
(1) 等效电路理论只考虑一维纵向振动,将结构件等效为实心体。该水听器模型通过计算接收灵敏度和导纳特性发现,接收灵敏度最大值约为170.7 dB,对应的频率约为23 100 Hz,接收灵敏度在200~10 800 Hz频段内起伏≤3 dB。
(2) 利用ANSYS有限元仿真,由模态分析得到水听器的一阶纵向谐振频率与一阶纵向反谐振频率分别为203 70.1 Hz和268 10.4 Hz,计算导纳特性,电导最大值所在频率与一阶纵向谐振频率相同,由谐响应分析得到的接收灵敏度曲线在一阶纵向反谐振频率附近存在峰值,约为-170.5 dB。大约在200~5 200 Hz频段内,接收灵敏度曲线起伏小于3 dB。当电阻()取极大值时,该点所处频率对应水听器的接收灵敏度曲线的峰值所处频率,即一阶纵向反谐振频率。此外,电抗曲线中波峰波谷对应的频率之间的带宽与水听器接收灵敏度反谐振频率处的-3 dB带宽大致吻合。
(3) 由等效电路理论和ANSYS有限元仿真得到的接收灵敏度最大值对应的频率分别在231 00 Hz和27 400 Hz处,有15.7%的误差,并且接收灵敏度在数值上存在差异。两种方法计算出的导纳曲线中,一阶纵向谐振频率分别约为20 750 Hz与20 600 Hz。
[1] 莫喜平. 功能材料及其应用于换能器技术的研究进展[J].物理, 2009; 38(3): 149-156
MO Xiping. Functional materials and their research progress in transducer technology[J]. Physics, 2009, 38(3): 149-156.
[2] 周福洪. 水声换能器及基阵[M]. 北京: 国防工业出版社, 1984: 7-8, 63-72
ZHOU Fuhong. Hydroacoustic transducer and array[M]. Beijing: National Defence Industry Press, 1984: 7-8, 63-72.
[3] WORCESTER P F. Deep-water ocean acoustic propagation: observations[J]. J. Acoust. Soc. Am., 2015, 138(3): 1842.
[4] WUNSCH C. Ocean acoustic tomography: past, present, and maybe future[J]. J. Acoust. Soc. Am., 2015, 138(3): 1818.
[5] WALKER D A. Deep ocean seismology[J]. Eos, Transactions American Geophysical Union, 1984, 65(1): 2-3.
[6] SONG H C. Diversity combining for long-range acoustic communication in deep water using a towed array[J]. J. Acoust. Soc. Am., 2012, 132(2): 68-73.
[7] 桑永杰. 低频宽带水声换能器研究[D]. 哈尔滨: 哈尔滨工程大学, 2014: 34.
SANG Yongjie. Low frequency broadband underwater acoustic transducer research[D]. Harbin: Harbin Engineering University. 2014: 34.
[8] 莫喜平. ANSYS软件在模拟分析声学换能器中的应用[J]. 声学技术, 2007, 26(6): 1280-1290.
MO Xiping. Application of ANSYS software in simulation analysis of acoustic transducer[J]. Acoustic Technology, 2007, 26(6): 1280-1290.
[9] 何作镛, 赵玉芳. 声学理论基础[M]. 北京: 国防工业出版社, 1981: 245-246, 329-332
HE Zuoyong, ZHAO Yufang. Acoustic theory foundation[M]. Beijing: National Defense Industry Press, 1981: 245-246, 329-332.
[10] 刘爽. 新型矢量水听器研究[D]. 哈尔滨: 哈尔滨工程大学, 2016: 65.
LIU Shuang. New vector hydrophone research[D]. Harbin: Harbin Engineering University, 2016: 65.
Comparative research on equivalent circuit and finite element analysis of longitudinal vibration type low-frequency piezoelectric hydrophones
XU Yan-zhe, FAN Gui-fen, TIAN Feng, DENG Hao-yuan, HU Hong-ping, LYU Wen-zhong
(The School of Optical and Electronic Information, Huazhong University of Science & Technology,Wuhan 430074, Hubei, China)
The equivalent circuit theory and ANSYS Finite Element Simulation are used to calculate the performance parameters of longitudinal vibration type composite rod piezoelectric hydrophone, and the two calculation results are compared. It is shown that the resonant frequencies of the receiving sensitivity obtained by the two methods are not in the same place, and there are some differences in the value of receiving sensitivity, and that the bandwidths of receiving sensitivity are all rather wide in the lower frequency band far from the resonance point. It is known that the equivalent circuit theory only considers the one-dimensional longitudinal vibration and idealizes the model. However, the ANSYS finite element analysis considers the longitudinal and transverse modal coupling of the whole model structure, which is closer to the actual model. Therefore, ANSYS has more advantages in the simulated optimization design of hydrophone. The equivalent circuit theory can provide theoretical guidance for finite element simulation because of its obvious physical significance.
equivalent circuit theory; ANSYS finite element simulation; reception sensitivity
TB565.1
A
1000-3630(2019)-06-0710-06
10.16300/j.cnki.1000-3630.2019.06.019
2018-05-31;
2018-06-28
中央高校基本科研专项资金,华中科技大学(2016JCTD114)
徐言哲(1995-), 男, 湖北宜昌人, 硕士研究生, 研究方向为水声换能器与有限元仿真。
吕文中, E-mail: lwz@hust.edu.cn
