扩展经验正交函数沿海声层析的声速反演

张姚滢，王洁，郑红，徐英超，尹会听

扩展经验正交函数沿海声层析的声速反演

张姚滢，王洁，郑红，徐英超，尹会听

(浙江海洋大学，浙江舟山 316000)

为了实现沿岸海域声速的实时连续监测，针对目前单收发换能器沿海声层析系统的剖面反演声线不足和接收信号不稳定的问题，提出了双收发换能器沿海声层析(Double-transcever Coast Acoustical Tomography, DCAT)系统。通过计算机进行仿真模拟，结果表明DCAT系统声速反演精度提高了一个数量级，验证了该系统对存在问题的改善及其有效性。在声速反演过程中，通过使用扩展经验正交函数(Extension Empirical Orthogonal Function, EEOF)表示声速剖面，实现了剖面全水深的声速反演。DCAT系统的提出和EEOF方法的应用，为海上实时连续观测系统的建立及数据处理，提供了理论基础和有效的实施方法。

双收发换能器沿海声层析系统；扩展经验正交函数；声速剖面反演

0 引 言

海洋声速及其变化是重要的海洋环境参数，而在沿岸海域对海洋环境观测的活动中，对海洋声速及其变化的监测极其重要。目前，声速剖面的监测反演，多数使用低频或爆炸声源水平或垂直接收阵列收集数据[1]，其中的声速通过经验正交函数[2-3]表示，反演方法使用匹配场方法[4-5]，亦有用同化方法处理数据[6]。

针对沿岸海域航运和渔业活动多发，使得设置接收阵列长期收集数据无法保证设备安全，收发器过多也导致了活动成本过大，本文提出了利用海洋声层析方法[7-8]，使用少量收发器，并且将收发器安装在岸基上，实现沿海声速剖面长期实时监测。

沿岸海域地形复杂、水深变化大，对于声速的表示方法若按照传统的经验正交函数，只能表示最小水深以内的声速，无法得到全水深的经验正交函数展开。针对观测数据为有限水深的情况，必须将原始数据进行延拓。利用广义数值环境模式延拓深水区声速的表示方法[9]在深海有效，但不适用于沿岸地形多变的情况。根据沿岸海域温度和盐度的分布特点，本文提出了一种简单的延拓方法，可以在水深变化的情况下，在全水深范围使用扩展经验正交函数(Extension Empirical Orthogonal Function, EEOF)表示声速剖面，为沿岸海域实时声层析反演声速提供了支撑。

1 沿海声层析原理

自从MUNK等[10]提出海洋声层析这一理论以来，无论在远海还是在近海均取得很大的突破。国内外学者针对沿岸海域声层析进行了很多研究[11-13]。为了达到沿海声速长期实时监测的目的，本文设计了适用于长时间安装在岸基上的双收发换能器沿海声层析(Double-transducer Coast Acoustical Tomography, DCAT)系统，通过数据处理提取出每个收发换能器往来传输的到达时间，反演呈现出被测量截面的声速分布数据。经过数值计算和模拟仿真，检验并确认了DCAT系统构成的有效性以及反演算法的可行性。

1.1 DCAT系统

对沿海声层析观测系统[14]的主要设计改进是将原先的单收发换能器装置改进成为双收发换能器系统装置，图1是DCAT系统构造图。在实验海域某一断面的左右两端各安置一个基站，并且每个基站两个不同水深处放置同类型收发换能器，同时配备全球定位系统(Global Positioning System, GPS)和数据通信系统；发送信号经过发射信号功放放大驱动换能器发送声波，在海域内传播后的声信号被接收换能器接收后转换成为电信号、再经信号放大、数据采样手段获取得到发送信号的数据，接收到的数据处理之后输送到数据存储中心作为后期声速反演的数据依据。系统控制单元统筹控制，设置好时间间隔使系统重复发射、接收、数据处理以及数据传输的工作。经过GPS时间同步，各个站点的换能器同时间发射信号；各站点发射信号后转入接收信号状态，等接收完其他基站换能器到来的信号之后，经过处理和传输，系统进入低能耗状态，直至下次工作启动。

系统将根据发送与接收的时延差得到声波在各站点之间的水中传播时间。反问题模型作为计算依据，利用各基站之间的传播时间对声速进行反向计算，最终将反向计算得到声速剖面数据。将数据即时反馈到基地中心站，在基地中心站反演并在界面中显示结果，这就完成了实时的声速分布观测。

由两基站之间的二维垂直声速分布，向三维声速分布，可考虑在整个实验海区设置多个基站，两两基站反演出的声速三维图像，实现海域内三维声速分布的反演重构。

图1 DCAT系统构造图

1.2 海洋声层析原理

海洋声层析原理是利用海洋环境参数对声传播的影响，通过测量声学参数的变化来反演海洋环境参数。根据声传播的声线理论，声波沿声线双方向传播时间可以表示为[10]

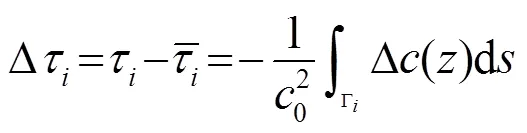
2 扩展经验正交函数(EEOF)

经验正交函数被普遍应用在声速剖面表达上，其使用只要确定几个系数即可，计算快捷方便[16]。传统经验正交函数(Empirical Orthogonal Function, EOF)理论是按照最浅水深的声速样本矩阵得到经验正交函数，并取前阶表示声速扰动量[10]。换而言之，这片海区的声速扰动使用个正交基表达。

海底地形的不规则性，也导致了经验正交函数无法用于表示全水深的声速。声速实测数据是由温盐深测量仪(Conductivity-Temperature-Depth System, CTD)获取，得到的是大量的不同深度下的声速数据。就深度较大的监测点来说，使用经验正交函数展开方式表达也是必要的。

扩展经验正交函数(Extension Empirical Orthogonal Function, EEOF)，是在经验正交函数的基础上，增加延拓扩展，而这个延拓扩展，使声速扰动两矩阵的秩不增加，并且其误差与传统的EOF相当。该方式使得声速表示在深水区内的误差变动为最小。

2.1 扩展基本原理和方法

由历史资料以及记载沿海温盐垂直变化规律的文献中[17]可知，沿岸水域深度有限，在潮流推动的作用下，深层的温盐会有一定的混合，使得一定深度以下温度与盐度有近似值。基于这点，产生一种扩展方式为等数值扩展温盐至最大水深，其声速扰动量随深度呈现线性相关，即声速扰动量矩阵是保秩的。

可得到的数据预处理步骤如下：

(1) 对采集的温盐深数据进行预处理。将原始数据中深度小于0的数据删除；多组温盐数据在相同深度下求取平均值作为该深度对应的温度和盐度数值。

(2) 对步骤(1)中所得数据进行等值扩展。依据测量剖面的地形结构，确保扩展深度值是剖面最大水深值，获取等深度间隔的声速数据。

(3) 按公式(4)计算得到不等深度下的声速值，对每个声速样本都使用三次样条插值方法，获取等深间隔的声速分布。

将最终得到的声速数据进行平滑处理，构造出全水深的声速样本矩阵。最终，EEOF的构建实现了全水深声速剖面的经验正交函数表示。

选取前个特征值对应的特征向量用以表示声速剖面[4]，那么任意位置的声速可以表示为

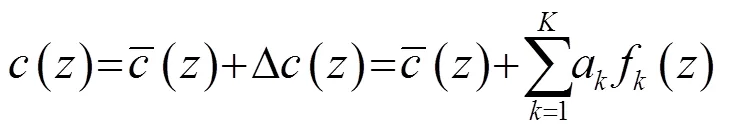
2.2 扩展结果检验

图2 实验海区66次CTD测量数据计算的声速剖面

表1 不同深度范围的数据样本数

如果采用传统的EOF方法计算声速剖面经验正交函数，将测量到的66组数据作为样本，计算的范围只能在0～10 m深度内，记为EOF10；使用2.1节的方法计算声速剖面的扩展经验正交函数如图3所示，可将实际测量获得的数据扩展至30 m，记为EEOF30；分别整理EOF10和EEOF30的前五阶，拟合原始测量数据，计算均方根误差，公式如式(5)所示：

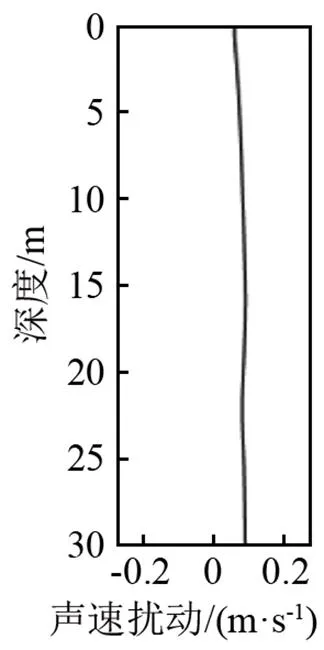
66组实测数据的均方根误差统计数据如表2所示。通过误差数值可判断两种经验正交函数前五阶展开拟合数据的误差在一个数量级。得到的EEOF30并没有明显的劣势，证明了使用EEOF表示声速剖面方法的可行性。

表2 实测数据的偏差统计结果(m·s-1)

3 声层析声速反演

根据式(3)可知，通过测量计算获得各个基站的声线到达时间，可反演得到声速剖面。声速反演分两部分进行计算仿真模拟：(1) 声线模型的正问题计算，应用传统声线模型仿真计算获得各基站间的声线传播时间(等效实际测量数据)以及声线轨迹，获得的数据用于反问题中的输入参数，保留此时的背景声速剖面用于对比反演结果的基准值；(2) 声速剖面的反问题计算，使用(1)中获得的数据反演计算声速剖面数据。通过对比背景声速剖面，评价反演结果。

3.1 正问题：声线模型

依据声线理论，当确定海域的背景声速之后，声波在水中会按照既定的传播路径以及传播时间传播，因此使用声线追踪方法[18]求解本征声线。CTD测量获得的温盐深数据可计算得到声速数据，所以当温盐深变化时声速随之变化，进而影响声传播的本征声线也发生改变。

若使用2.2节中前五阶EEOF30表示被反演的某一时刻声速剖面背景声速时，反演就是求EEOF30的5个系数，为了求出这5个参数，至少需要5个独立方程，即5条独立声线，并且声线要覆盖反演断面以保证整个剖面的反演精度。但是对于单收发换能器系统，在温盐深观测数据发生变化时，并不能确保5条以上独立声线存在，因此在2.1节提出了DCAT系统，通过调整收发换能器的位置，使得在温盐深观测数据发生变化时，也能确保充足的独立声线数量，并能让声线覆盖反演断面。

通过多次的模拟计算，证明将同侧的收发换能器垂直方向安装位置的距离增加，会提高声线的独立性以及在断面上的空间覆盖率，但是深度的增加导致海底的反射次数增多和信号的衰减，也增加了现场布置难度。实际水文条件的复杂性增加了收发换能器安置点的选择困难性，所以在实际应用时，只综合考虑独立声线的分布以及收发换能器安置的便捷性。

图4是在实验海区中某个断面计算得到的声速剖面以及声线轨迹图，其中左图为背景声速剖面分布，右图为通过声线模型计算所得的声线轨迹图。从图4可知，断面两端距水面以下2 m和5 m处分别放置两个收发换能器，声速剖面最大深度为30 m，水深变化范围从9～29 m，计算获得15条本征声线，其中本征声线到达的最大水深为21.1 m。图中独立本征声线数大于5条，并且本征声线基本覆盖了监测断面。因而，计算获得的本征声线将用于以下的反演计算即反问题计算。

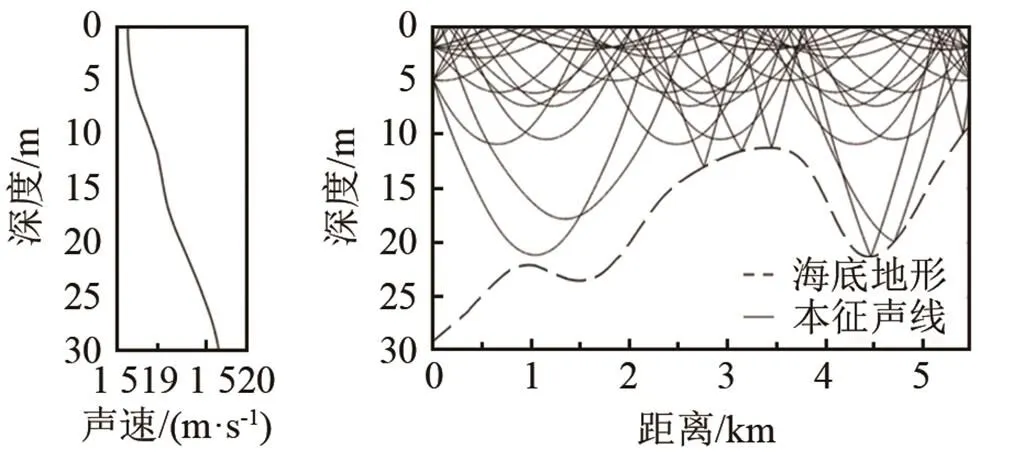
(a) 背景声速剖面分布 (b)声线模型计算所得的声线轨迹图

3.2 反问题：声速反演仿真

求解方程组，通过利用经验正交函数展开关系式(4)，声速扰动用前阶经验正交函数表示为

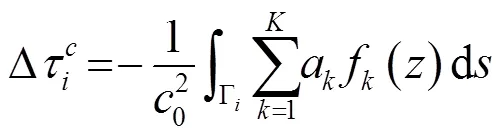
写成矩阵形式：

或写成标准矩阵方程：

这样，反演问题转换为解矩阵方程。在实际计算中，因为原方程的不适定性，矩阵方程(8)常常也是非满秩病态的。为了稳定求解方程(9)，通常将其转化成优化问题来求解，即为目标函数求最优化：

3.3 声速反演仿真结果

利用3.1节计算获得的声线到达路径和传播时间，根据3.2节的方法进行反演计算，获得声速剖面的数据分布如图5所示。图5在声线到达的深度范围内反演获得的声速与背景声速能较好地吻合，在0～20 m内均方根误差为0.008 3 m·s-1。

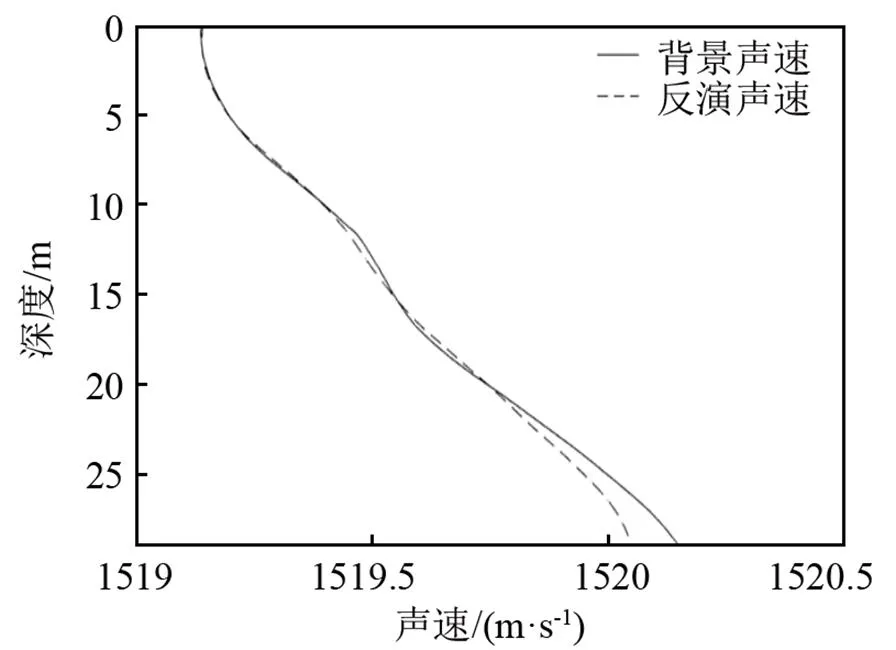
图5 利用EEOF30声速反演结果与背景声速的比较

为了验证DCAT系统的性能，采用同样的反演算法与单收发换能器沿海声层析(Single-transducer Coast Acoustical Tomography, SCAT)系统的声速反演结果进行比较，如表3所示，表中均方根值是根据公式(5)计算得到。从表3可以得到以下几点：

(1) 在DCAT系统中，深度0～20 m范围均方根误差为0.008 3 m·s-1，在0～29 m范围均方根误差(0.031 5 m·s-1)明显增大，其中本征声线能够到达的最大水深为21.1 m，因此反演的有效深度与本征声线所能到达的深度有关。而在实际应用时要设计发射接收深度，使声线覆盖反演区域。

(2) 比较SCAT系统和DCAT系统，使用DCAT系统模拟仿真获得的本征声线数量多，产生的信息量更大；使用DCAT系统之后，声速反演精度明显提高，在不同的深度范围内，均方根误差都相差一个数量级；

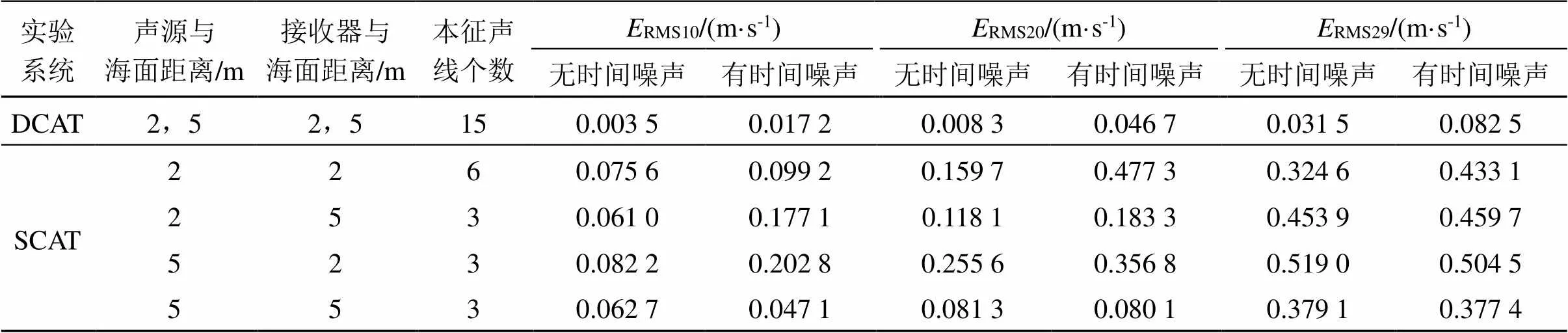
表3 DCAT系统与SCAT系统比较

4 结论

DCAT系统的提出，实现了沿岸海域声速反演的实时监测，与传统的SCAT系统相比获得的信息量更大，反演精度提高了一个数量级；同时，DCAT系统的稳定性也有所提高。

反演过程中，利用经验正交函数反演声速只需要计算各阶经验正交函数的系数即可，提高了计算速度。但是，由于沿海海域海底地形复杂，传统的方法无法得到全水深的经验正交函数，因此本文提出了用EEOF表示声速剖面的方法，并且通过计算比较，确立了该方法的有效性，为全水深声速反演奠定了基础。

基于声线传播时间反演声速的理论，通过仿真计算进行声速反演。结果表明，反演的有效深度与本征声线所能到达的深度有关。在本征声线所能到达的深度范围内，反演的声速剖面与实际声速剖面的均方根误差很小。

DCAT系统和EEOF的提出以及计算仿真的验证，为海上实际观测系统的建立提供了理论基础。由于实际海洋观测环境远比模拟仿真复杂，除收发器位置和声速分布以外，实际海底地形、潮位的变化、声速跃层的变化等都会影响传播声线，很难有确定的最佳设计方案用于多变的海洋环境。但是，通过适当设置收发器的位置，使得传播声线尽量覆盖反演断面，就可以获得一定精度的声速剖面反演结果。在必要时还可以增加收发器的数量，达到声线覆盖观测断面的目的，当然这也会增加系统的复杂性和成本。

[1] 李风华, 张仁和. Inversion for sound speed profile by using a bottom mounted horizontal line array in shallow water[J]. 中国物理快报: 英文版, 2010, 27(8): 106-109.

LI Fenghua, ZHANG Renhe. Inversion for sound speed profile by using a bottom mounted horizontal line array in shallow water[J]. Chinese Physics Letters: English, 2010, 27(8): 106-109.

[2] 沈远海, 马远良, 屠庆平, 等. 浅水声速剖面用经验正交函数(EOF)表示的可行性研究[J]. 应用声学, 1999, 18(2): 21-25.

SHEN Yuanhai, MA Yuanliang, TU Qingping. Feasibility of description of the sound speed profile in shallow water via empirical orthogonal function (EOF)[J]. Applied Acoustics, 1999, 18(2): 21-25.

[3] 沈远海, 马远良, 屠庆平. 声速剖面的分层经验正交函数表示[J]. 西北工业大学学报, 2000, 18(1): 90-93.

SHEN Yuanhai, MA Yuanliang, TU Qingping. On expression of ocean sound profile by layered empirical orthogonal function (EOF)[J]. Journal of Northwestern Polytechnic University, 2000, 18(1): 90-93.

[4] 何利, 李整林, 张仁和, 等. 东中国海声速剖面的经验正交函数表示与匹配场反演[J]. 自然科学进展, 2006, 16(3): 351-355.

HE Li, LI Jilin, ZHANG Renhe, et al. The empirical orthogonal function of the sound speed profile in the east China sea and the inversion of the matching field[J]. Progress of Natural Science, 2006, 16(3): 351-355.

[5] TOLSTOY A, SOTIRIN B. Ocean tomography via matched-field processing[J]. J. Acoust. Soc. Am., 1991, 89(5): 393-406.

[6] LI J L, JIN L L, XU W. Inversion of internal wave-perturbed sound-speed field via acoustic data assimilation[J]. IEEE Journal of Oceanic Engineering, 2014, 39(3): 407-418.

[7] FLATTÉ S M. Ocean acoustic tomography[J]. Eos Transactions American Geophysical Union, 2013, 77(17): 166-166.

[8] SKARSOULIS E K, ATHANASSOULIS G A, SEND U. Ocean acoustic tomography based on peak arrivals[J]. J. Acoust. Soc. Am., 1996, 100(2): 797-813.

[9] 张旭, 张永刚, 张胜军, 等. 经验正交函数与广义数值环境模式重构声速剖面的比较[J]. 应用声学, 2010, 29(2): 115-121.

ZHANG Xu, ZHANG Yonggang, ZHANG Shengjun, et al. A comparison between the EOF and GDEM methods for reconstruction of sound speed profile[J]. Applied Acoustics, 2010, 29(2): 115-121.

[10] MUNK W, WORCESTOR P F, WUNSCH C. Ocean acoustic tomography[M]. Cambridge University Press, 1995: 6-9.

[11] WORCESTER P F, CORNUELLE B D, SPINDEL R C. A review of ocean acoustic tomography: 1987-1990[J]. Reviews of Geophysics, 1991, 29(S2): 557-570.

[12] 廖光洪, 朱小华, 林巨, 等. 海洋声层析应用与观测研究综述[J]. 地球物理学进展, 2008, 23(6): 1782-1790.

LIAO Guanghong, ZHU Xiaohua, LIN Ju, et al. Review on application and observation of ocean acoustic tomography[J]. Geophysics Progress, 2008, 23(6): 1782-1790.

[13] JIN L, JIANLONG L I, WEN X U. Tracking of time-evolving sound speed profiles with an auto-regressive state-space model[J]. Chinese Journal of Acoustics, 2017(3): 302-312.

[14] ZHENG H, YAMAOKA H, GOHDA N, et al. Design of the acoustic tomography system for velocity measurement with an application to the coastal sea[J]. Journal of the Acoustical Society of Japan, 1998, 19(3): 199-210.

[15] TIKHONOV A N, ARSENIN V Y. Solutions of ill-posed problems[M]. Winston: Mathematics of Computation, 1977: 491-491.

[16] 沈远海, 马远良, 屠庆平, 等. 浅水声速剖面的反演方法与实验验证[J]. 西北工业大学学报, 2000, 18(2): 212-215.

SHEN Yuanhai, MA Yuanliang, TU Qingping. Inversion of sound speed profile for shallow-water environment with experimental verification[J]. Journal of Northwestern Polytechnic University, 2000, 18(2): 212-215.

[17] 刘兴泉, 侯一筠, 尹宝树. 东海沿岸海区垂直环流及其温盐结构动力过程研究, Ⅱ. 温盐结构[J]. 海洋与湖沼, 2004, 35(6): 19-28.

LIU Xingquan, HOU Yijun, YIN Baoshu. In the east China sea coastal sea area vertical circulation and thermohaline structure dynamic process research, Ⅱ. Thermohaline structure[J]. Journal of oceans and lakes, 2004, 35(6): 19-28.

[18] JENSEN F B, KUPERMEN W A, PORTER M B, et al. Computational ocean acoustics[M]. New York: AIP Press, 1994: 155-230.

The sound velocity inversion by EEOF coast acoustical tomography

ZHANG Yao-ying, WANG Jie, ZHENG Hong, XU Ying-chao, YIN Hui-ting

(Zhejiang Ocean University, Zhoushan 316000, Zhejiang, China)

s:In order to realize the real-time continuous monitoring of sound speed along coastal waters, a Double-transcever Coast Acoustical Tomography (DCAT) system is proposed in this paper. The main purpose to do so is to solve the problem on the insufficiency of acoustic ray inversion and the instability of receiving signal in the existing single-transcever coastal acoustic tomography system. The results obtained by computer simulation show that the sound speed inversion precision of DCAT system can be improved by one order of magnitude, which verifies the effectiveness of the system. In the process of sound speed inversion, the Extended Empirical Orthogonal Function (EEOF) is used to represent the sound speed profile and to realize the sound speed inversion of the whole water depth of the section. The DCAT system and EEOF method provide a theoretical basis and an effective way for the establishment and data processing of the real-time continuous observation system.

double-transcever coast acoustical tomography (DCAT) system; extension empirical orthogonal function (EEOF); inversion of sound-speed profile

O422.1

A

1000-3630(2019)-06-0617-06

10.16300/j.cnki.1000-3630.2019.06.003

2018-05-10;

2018-07-20

国家海洋局2015年海洋公益性行业科研专项(201505003、201505025)、浙江海洋大学科研启动基金(21105011813)。

张姚滢(1994－), 女, 浙江绍兴人, 硕士研究生, 研究方向为海洋声学仪器装备。

王洁,E-mail: wangjie19790908@163.com; 郑红, E-mail: zhenghong@zjou.edu.cn