柔性元件对同振式矢量水听器接收性能影响研究*
2015-03-15谢攀张恺
谢 攀 张 恺
(海军工程大学兵器系 武汉 430033)
柔性元件对同振式矢量水听器接收性能影响研究*
谢 攀 张 恺
(海军工程大学兵器系 武汉 430033)
建立了同振球型矢量水听器的物理模型,利用该模型研究了柔性元件对水听器工作频率、振速幅值和相移等性能参数的影响规律。结果表明:水听器尺寸一定时,柔性元件弹性系数越小,水听器下限工作频率越低,一般在零点几到几赫兹之间;柔性元件主要影响低频段振速幅值测量,且弹性系数越大,影响越大,而振速测量过程中由柔性元件引起的相移几乎为零,可忽略不计。
同振式矢量水听器; 柔性元件; 下限工作频率; 振速幅值; 相移
Class Number TP212
1 引言
矢量水听器是由声压水听器和质点振速水听器复合而成的能同时测量声压信息和质点振速信息的新型水听器[1~3]。其低频指向性好,空间增益高[4],较传统声压水听器及其基阵体积更小,可设计为水下小尺度平台声学探测装置。根据工作原理的不同,矢量水听器可分为压差式矢量水听器和同振式矢量水听器,其中,同振式矢量水听器能够直接测量声场中的质点振速,本身不产生明显的声场畸变,可以视为点接收器,而且性能参数稳定,在民用和军事领域都有着广泛的应用前景。
同振式矢量水听器一般由内置传感器、外壳、与外壳连接的柔性元件组成,其中柔性元件通常采用橡皮绳或弹簧。实际工程应用中,同振式矢量水听器通过柔性元件悬置于大质量框架上,从而能有效隔离平台振动对矢量水听器的影响,保证水听器的时间平均位置[5~6]。国内外对同振式矢量水听器的研究主要集中于内置传感器设计与改进上,对于外围柔性元件的研究较少。而作为矢量水听器中的关键元件,其结构参数直接影响矢量水听器的接收性能,因此,为了更好地掌握柔性元件对矢量水听器接收性能的影响,本文以同振式矢量水听器为研究对象,通过建立相应的力学模型和等效电路模型,分析柔性元件对工作频率,振速幅值和相移等性能参数的影响,为其中柔性元件设计提供理论依据。
2 振动模型分析
目前国内外常用的矢量水听器的悬挂方式有两根柔性元件垂直悬挂、六根柔性元件互相垂直悬挂、八根柔性元件垂直悬挂和八根柔性元件倾斜悬挂[7]。本文考虑将同振球型矢量水听器通过六根互相垂直的弹性系数为K的弹簧悬置于大质量框架上。如图1所示,柔性元件的初始长度为l0,水听器固定于原点O时柔性元件被拉伸变为l,此时各柔性元件的变形量均为Δl=l-l0。
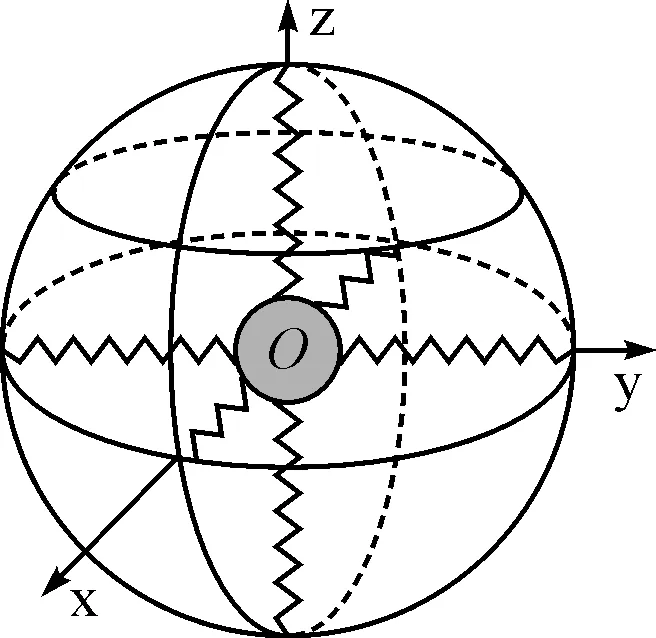
图1 同振球型矢量水听器悬置示意图

图2 同振球型矢量水听器振动示意图
为便于讨论,本文根据同振球型矢量水听器的工作原理以及悬挂系统的特性,假设:水听器的外形尺寸远远小于声波波长,几何中心与重心重合,且平均密度等于水介质的密度;平面声波在XOY平面内入射到水听器上,水听器在入射方向上以原点为中心做微幅振动,不做旋转运动,且只考虑柔性元件的纵向拉伸力,而忽略其他方向作用力。图2所示即为矢量水听器的振动示意图,它的动力学模型可以表示为一个单自由度的球体—柔性元件振动系统。为了直观地表示矢量水听器的受力情况,采用等效电路法分析此系统的动力学特性。
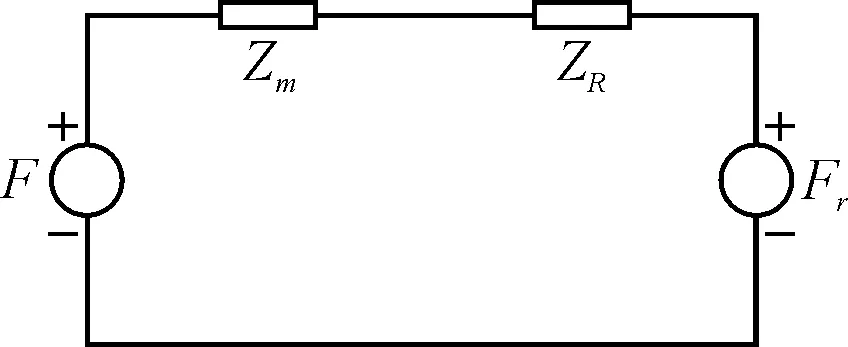
图3 矢量水听器等效电路模型
如图3所示,F为声压作用于球体表面的作用力,Fr为柔性元件在外界刺激作用下对水听器的总作用力,Zm和ZR分别表示自由球体在水中运动时的机械阻抗和辐射阻抗。
由声学理论知识可知[8]:
(1)
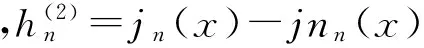
由文献[9]可知作用力Fr为
Fr=j·2K(3-2l0/l)·Vc/ω
(2)
由于l0及l已知,所以当柔性元件弹性系数K一定时,Fr只与水听器的振速幅值Vc和入射声波角频率ω有关。
耳聋分为神经性、传导性和混合性三类,神经性耳聋是因感音神经出现障碍;传导性耳聋是因内耳有炎症,有积水;混合性耳聋是上面两种因素交叉引起的。如果发现老人听力下降,可进行纯音测听、声导抗和耳声发射等检查,然后对症下药。
Zm,ZR分别为[10]
(3)
式中,M为矢量水听器的质量,ρ水为水介质密度,c水为水中声波传播速度。
故矢量水听器和柔性元件组成的球体—柔性元件振动系统总机械阻抗为[11]
(4)
当系统的总机械阻抗的虚部为零时,系统发生谐振,由此可求得此系统的谐振频率为
(5)
当接收面在声波作用下产生振动时,作用在接收器表面的作用力F与其接收面的实际振速幅值Vc之间的关系为:Vc=F/Z总。又入射声波在球心处的质点振速为vw(t)=Vwejωt=(p0/ρ0c水)ejωt,故结合式(4)可得水听器振速幅值与水质点的振速幅值比为
(6)
相位角φ为
(7)
其中E=2K(3-2l0/l)/ω2,它是一个与柔性元件弹性系数K及声波频率ω有关的参数。
在矢量水听器实际使用过程中,内置传感器的谐振频率控制着矢量水听器的上限工作频率,而球体柔性元件振动系统的谐振频率决定着矢量水听器工作频率的下限。由式(5)、式(6)可知:柔性元件对矢量水听器接收性能的影响主要体现在两个方面:一是水听器工作频率的下限,二是水听器对质点振速的测量。
3 结果与分析
取l0=0.20m、l=0.25m,由式(5)可知矢量水听器下限工作频率f为
(8)
分别计算不同直径水听器的下限工作频率f随柔性元件弹性系数K的变化规律,结果见图4。由计算结果可知:当柔性元件
3.2 柔性元件对振速测量的影响
取水听器球体半径a=0.04m,l0=0.20m、l=0.25m,分析柔性元件对水听器所测振速幅值和相位的影响规律,结果见图5。计算结果表明:柔性元件对矢量水听器振速幅值测量的影响主要表现在低频段,且柔性元件的弹性系数K值越大,影响越大;而振速测量过程中由柔性元件引起的相移几乎为零,可忽略不计。
4 结语
本文以同振式矢量水听器工作原理及悬挂系统基本要求为基础,通过分析同振球型矢量水听器水下振动的物理模型及等效电路模型,研究了柔性元件对同振式矢量水听器接收性能的影响。研究结果表明: 1) 柔性元件对矢量水听器接收性能的影响主要体现在两个方面:一是水听器工作频率的下限,二是水听器对质点振速的测量; 2) 水听器尺寸一定时,柔性元件弹性系数越小,水听器下限工作频率越低,一般在零点几赫兹到几赫兹的范围内; 3) 柔性元件对振速幅值测量的影响主要表现在低频段,且柔性元件的弹性系数越大,影响越大; 4) 振速测量过程中由柔性元件引起的相移几乎为零,可忽略不计。
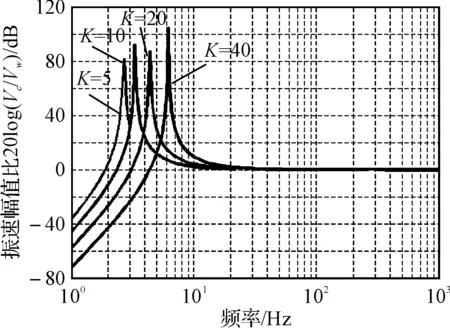

图5 柔性元件对矢量水听器振速测量的影响
[1] 孙贵青,李启虎.声矢量传感器研究进展[J].声学学报,2004,29(6):481-490.
[2] 孙贵青.矢量水听器检测技术研究[D].哈尔滨:哈尔滨工程大学,2001.
[3] Leslie C B, Kendall J M, Jones J L. Hydrophone for measuring particle velocity[J]. J. Acoust. Soc. Am,1956,28:711-715.
[4] 杨德森,洪连进.矢量水听器原理及应用引论[M].北京:科学出版社,2009:1-2.
[5] Kim K. Investigation of an underwater acoustic vector sensor[D]. Pennsylvania: The Pennsylvania state University,2002.
[6] 贾志富.三维同振型矢量水听器的特性及其结构设计[J].应用声学,2001,20(4):15-20.
[7] 张俊.潜标平台下的矢量水听器悬挂系统声学性能影响研究[D].哈尔滨:哈尔滨工程大学,2012.
[8] 何祚镛,赵玉芳.声学理论基础[M].北京:国防工业出版社,1981.
[9] 时胜国.矢量水听器及其在平台上的应用研究[D].哈尔滨:哈尔滨工程大学,2006.
[10] Morse P, Ingard U. Theoretical Acoustics[M]. Princeton: Princeton University Press,1968:128.
[11] 时胜国,杨徳森.弹性元件对同振型振速水听器的影响[J].应用声学,2004,23(5):21-26.
Effect of Flexible Element on Receiving Performance of Co-vibrating Vector Hydrophone
XIE Pan ZHANG Kai
(Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033)
A physical model of the vibrating sphere type vector hydrophone is established, and the flexible components influence on hydrophone frequency, vibration amplitude and phase shift performance parameters are studied by the model. The results show that when the hydrophone size is certain, the smaller elasticity of the flexible member, the lower limit on hydrophone lower working frequency, generally between a few tenths to a few hertz. Flexible components mainly affects the low frequency vibration velocity amplitude measurement, and the elastic coefficient is big, the greater the influence, and the phase shift caused by the flexible components in the process of velocity measuring is almost zero, negligible.
co-vibrating vector hydrophone, flexible components, lower working frequency, vibration amplitude, phase shift
2014年10月12日,
2014年11月29日
谢攀,男,硕士研究生,研究方向:武器系统运用与保障工程。张恺,男,博士研究生,研究方向:武器系统运用与保障工程。
TP212
10.3969/j.issn1672-9730.2015.04.038
