非常发性瓶颈区可变限速控制方法

朱 健，丁鹏程

(南京市城市与交通规划设计研究院股份有限公司，江苏 南京 210000)

随着快速路交通需求的不断增长，快速路上由于突发事故、临时道路施工等突发事件所导致的交通拥堵现象也越来越普遍，严重影响了快速路的运行效率和安全性。因此，需要对瓶颈点上游的车流进行控制，而可变限速控制是一种常用控制方法，能延缓车流顺利到达瓶颈点，从而提高快速路的通行效率和安全性。

针对瓶颈的可变限速控制方法，杨庆芳等[1]对元胞传输模型进行扩展，并采用阶梯限速控制方法对主线交通流进行控制。王希良等[2]基于元胞传输模型提出一种高速公路事故路段分区域可变限速控制方法，以车均延误和平均排队长度作为评价指标。蒋咏寒[3]根据瓶颈点通行能力陡降现象，提出一种结合可变限速和匝道的控制方法。段荟等[4]提出了一种基于Q学习算法的可变限速控制策略，通过遍历交通流状态集合，尝试不同限速值序列进行自适应学习。

目前的已有研究大多偏重于对主线瓶颈区开展研究，并未考虑非常发性瓶颈恢复后的可变限速控制方案，也没有从网络层面对辅路及周边路网的可变限速控制策略进行深入研究。因此，本研究考虑瓶颈发生至瓶颈恢复全过程的可变限速控制方案，并从路网层面研究速度限制对路网交通分配产生的影响，为快速路非常发性瓶颈可变限速方法提供了理论支持。

1 非常发性瓶颈区CTM模型改进

1.1 非常发性瓶颈特性

快速路上的交通拥堵通常是由于瓶颈点所导致，快速路瓶颈通常可分为两类，即常发性瓶颈和非常发性瓶颈，其中形成非常发性瓶颈区的原因主要包括交通事件、车辆货物散落等突发事件及计划安排等，导致部分车道关闭，从而使道路通行能力降低或交通需求急剧增加，进而形成瓶颈区。而此类瓶颈在时间和空间维度上具有较强的偶然性和突发性，易形成非周期性的交通拥堵。非常发性交通拥堵通常包括3个部分，即瓶颈形成、拥堵扩散及瓶颈恢复[5]，如图1所示。

图1 非常发性瓶颈形成及消散过程

1.2 元胞传输模型

元胞传输模型是由Daganzo(1994)[6]提出的一阶交通流模型，是对LWR流体理论模型的离散化近似。根据主线线形的不同，从上游至下游将主线分为M个基本路段，每个基本路段又可分为m个大小相同的元胞，元胞i为上游元胞，元胞i+1为下游元胞。

其中，输入元胞i的流量为

(1)

式中：Vm,i-1(k)，ρm,i-1(k)分别为元胞i-1的速度和密度；Qmax为元胞的通行能力；ρjam，ρC为阻塞密度和临界密度。

密度更新方程为

qm,i+1(k)+r(k)-s(k)).

(2)

式中：Δt为时间间隔；Lm,i为基本段m内元胞i的长度；λm,i为基本段m内元胞i的车道数；r(k)为匝道输入流量；s(k)为匝道输出流量。

速度-密度方程为

vm,i(k)=

(3)

式中：vf为自由流车速。

1.3 元胞传输模型扩展

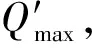
(4)

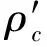
可推导出可变限速情况下自由流状态及拥挤状态下各元胞内的车流速度

vm,j(k)=

(5)

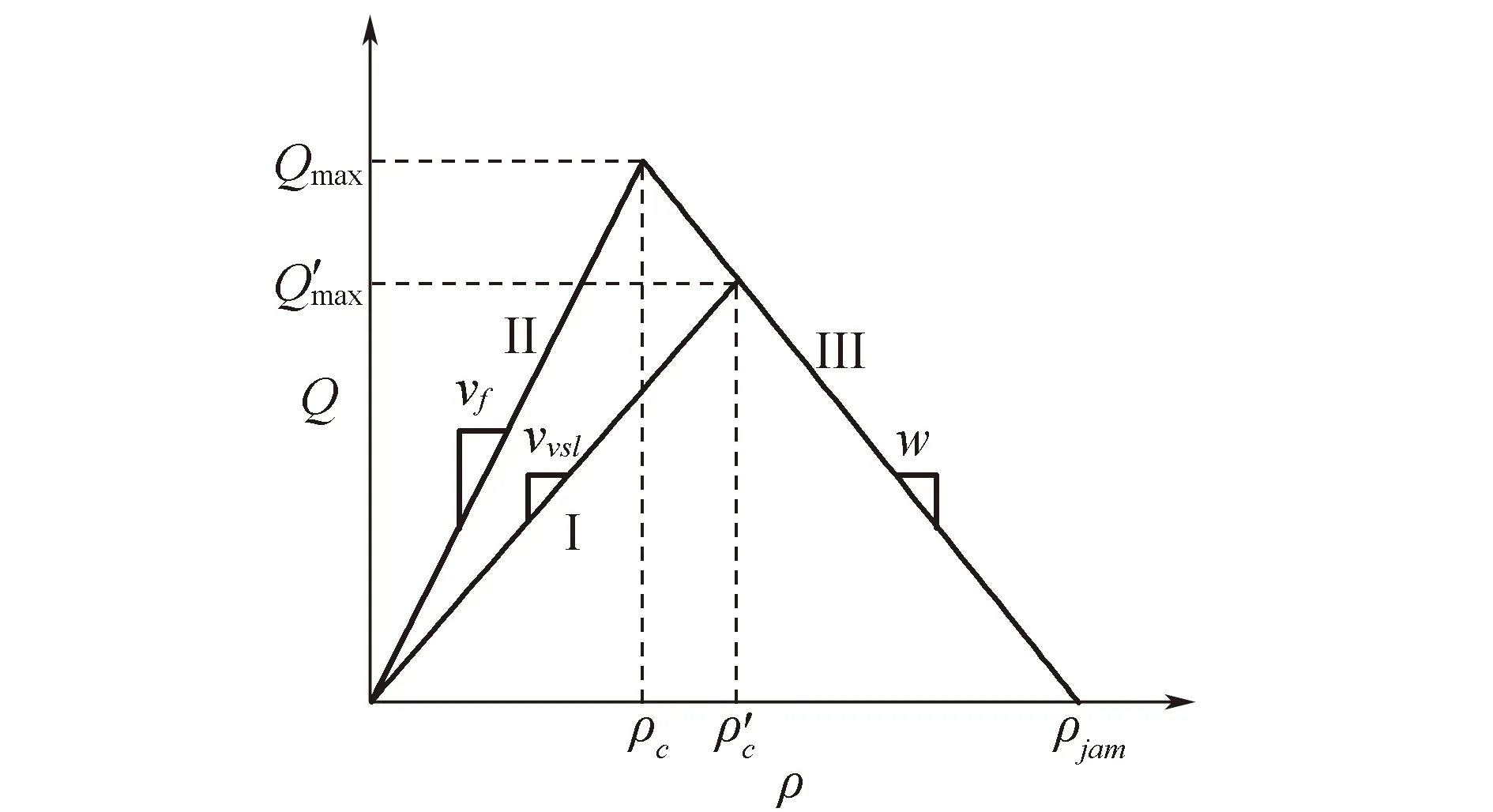
图2 可变限速情况下的流量-密度关系

则输入元胞i的流量为

(6)

由于瓶颈的存在，使得车辆在瓶颈点上游频繁换道和交织合流，导致车速降低，而通过瓶颈点下游时，车辆又必须从低速迅速提速至正常速度，此行为将使瓶颈点产生5%～20%的通行能力突降[7]。

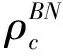
(7)

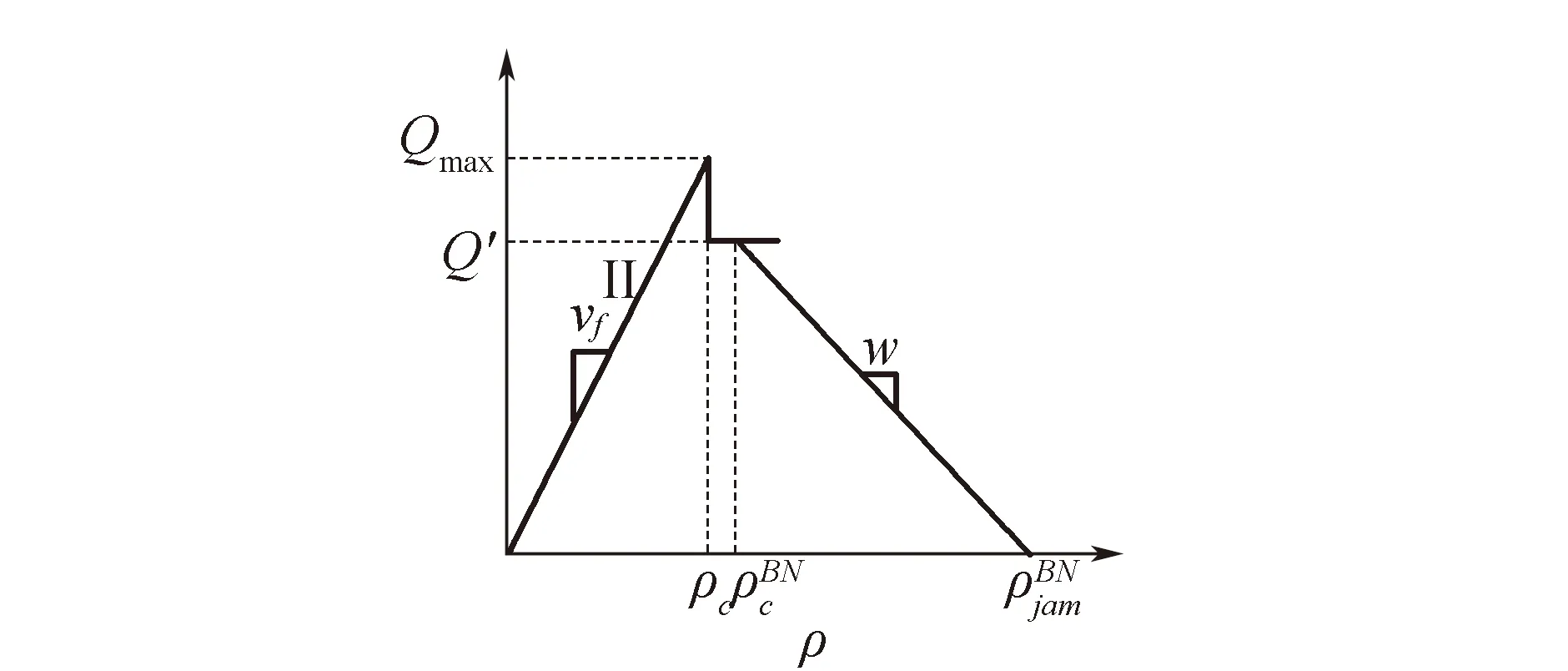
图3 瓶颈元胞通行能力突降示意图

1.4 瓶颈安全性分析

非常发性瓶颈区除了影响瓶颈段及其上游的通行效率外，也极大地影响了快速路上车流行驶的安全性。如图4所示，为瓶颈区上游至下游所观测到的车流速度分布情况[8]。从瓶颈区上游至中游，曲线的斜率变化情况逐渐增大，车速的波动性也逐渐增大，而从中游至瓶颈段时，斜率的变化情况则逐渐减小。

为降低交通事故发生的风险，需对中游路段至瓶颈区设置可变限速控制信息板，以避免车流速度突降的现象发生。快速路主线各基本段的限速为vm,vsl，各段内元胞i的限速值也为vm,vsl。为了安全考虑，使主线中游至下游瓶颈段内所有元胞内车流速度平滑地变化，相邻元胞内的车速变化值应为一个较小且稳定的限速值Δv，进而车速变化呈线性变化。

从中游至下游，将快速路主线划分为s个元胞，则从中游到瓶颈段s个元胞的车速理想值应为

[v3(k),v3(k)-Δv,v3(k)-2Δv,

…v3(k)-(s-1)Δv].

(8)

式中：v2(k)为主线下游瓶颈处的车速；v3(k)为主线中游的车速；s为主线中游至下游元胞个数。

相邻元胞内车速变化的理想值为

(9)

根据上述分析，使用从主线中游至瓶颈处，第s个元胞内的实际车速与理想车速之差H作为安全性指标

H=|vm,s(k)-[v3(k)-(s-1)Δv]|.

(10)

图4 中游至瓶颈段元胞理想车速分布

2 限速控制条件下路网均衡问题

2.1 限速对路段流量的调节作用

当快速路主线存在非常发性瓶颈时，采用可变限速控制后，部分出行者会选择更改路线，选择离开主线进入辅路及周边路网，从而使网络内流量发生变化，直至最终达到新的均衡。本文将路网界定为快速路主线、辅路及周边主次干道所组成的路网，研究非常发性瓶颈下可变限速控制对路网均衡的影响。

(11)

式中：La为路段a长度。

(12)

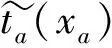
采用BPR函数作为行程时间函数

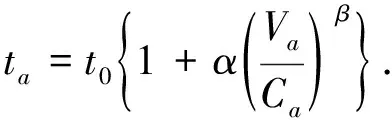
(13)

式中：t0为路段a流量为0时的阻抗，即自由流状态下的行程时间，Va为路段流量，Ca为路段a的实际通行能力，α和β为修正系数，一般取α=0.15,β=4。

图5 限速情况下路段速度-流量和时间-流量关系

2.2 瓶颈发生前路网均衡性分析

如图6所示，描述的是快速路主线、辅路及周边路网车流正常运行过程中，路网中某一路段流量的自我调节过程，横轴为时间T，纵轴为流量Q。路段的流量变化趋势可分为3类，即下降型、上升型和波动型(两个峰值之差较小)。

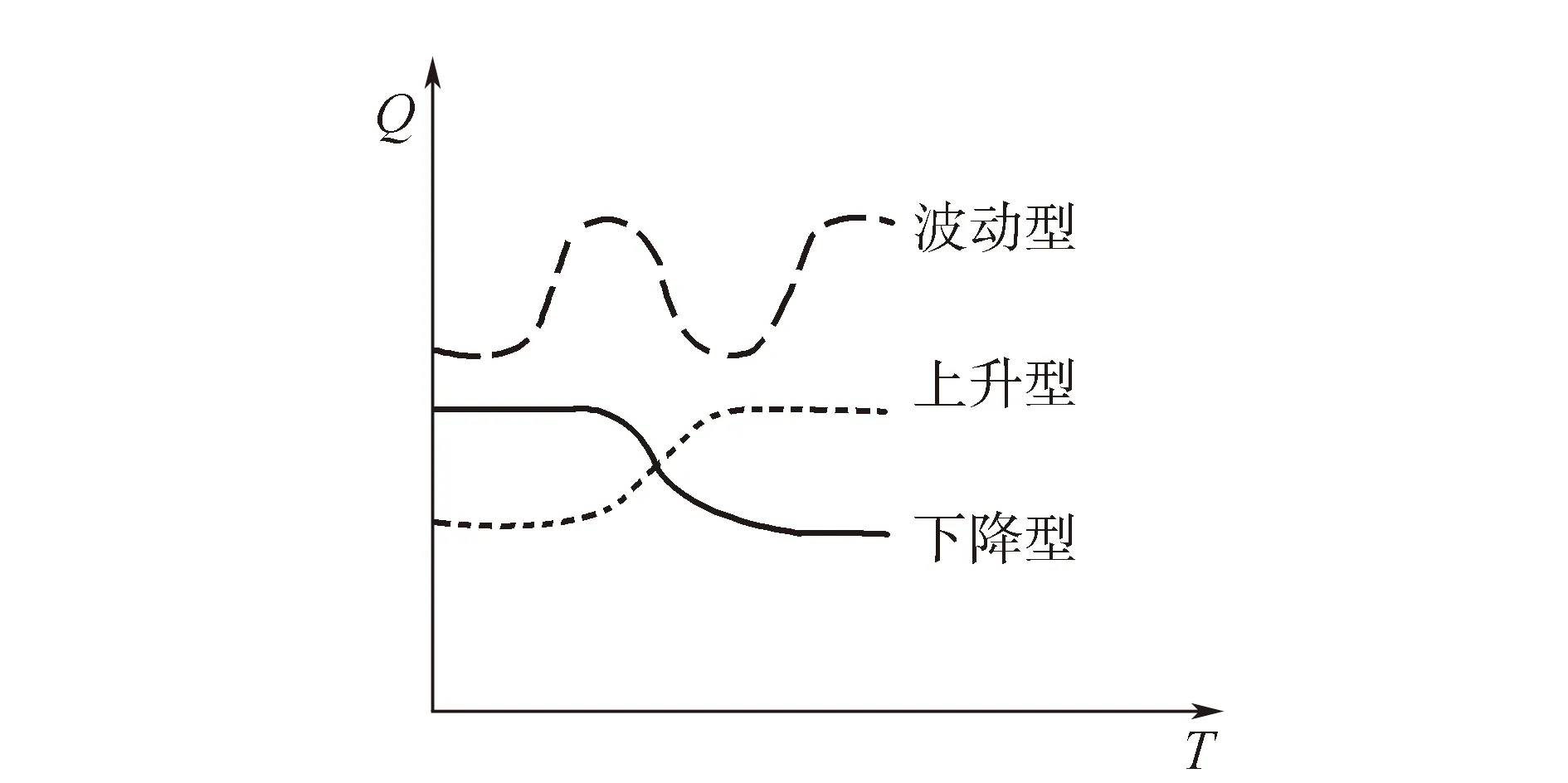
图6 路段流量调节3种类型

2.3 瓶颈发生后限速流量变化过程

如图7所示，以下降型为例，描述的是瓶颈恢复前路网未达到均衡和达到均衡两种情况。以前者为例，如图7中II所示，假设主线在tb时刻下游形成瓶颈，立即开启限速控制，直至t2时刻瓶颈恢复时，路网仍未达到均衡状态。此后，关闭车道恢复正常通行，瓶颈段通行能力提高，此时限速值需要提高，从而将辅路分流的流量重新调节回主线。在t3时刻，主线恢复正常限速值，且路网达到均衡状态。与此类似，如图7中III所示，路网在瓶颈恢复后才能达到均衡。

图7 瓶颈恢复前两种均衡情况

3 模型构建

3.1 上层快速路主线目标优化问题

在上层模型中，选用元胞传输模型来计算主线通行效率和安全性。根据非常发性瓶颈恢复与否，将控制目标分为两类。瓶颈发生至瓶颈恢复这段时间内，其主要控制目标包括主线车流总行程时间和安全性。而当瓶颈恢复后，控制目标为主线车流总行程时间。以各分区的限速值为决策变量构建模型，结果如下。

3.1.1 主线车辆总行程时间

选取主线所有车辆的总行程时间最小为控制目标

(14)

式中：t为时间步长，kp为总时间步长数，Nm为主线划分元胞总数，s为主线中游至瓶颈区划分元胞数。

3.1.2 安全性

根据1.4节中对于主线中游至瓶颈区车速变化的分析，其控制目标为实际车速与理想车速之差最小

(15)

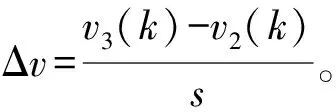
综上所述，瓶颈发生至瓶颈恢复时间段内，目标函数可描述为

(16)

式中：αD，αc为权重系数。

瓶颈恢复后，其目标函数可描述为

(17)

3.2 下层快速路网用户均衡配流问题

上下层之间互相依赖、互相影响，上层模型的VSL控制下各路段的流量输入会影响快速路网的行程时间，下层路网流量分布又会限制上层的VSL控制。在下层模型中，针对车道关闭及限速控制对出行阻抗的影响，出行者选择对其最有利的出行路径，因此，优化模型为限速条件下快速路网用户均衡配流模型[9-10]，其具体形式为

(18)

其中

(19)

(20)

式中：xa为路段a的流量；fr,w为w个OD第r路径的流量；δa,r为路段与路径的关联因子；dw为第w个OD的交通出行需求；Rw为第w个OD的路径集合。

最后，分别设计了遗传算法和Frank-Wolfe算法来求解上层和下层模型[11]。

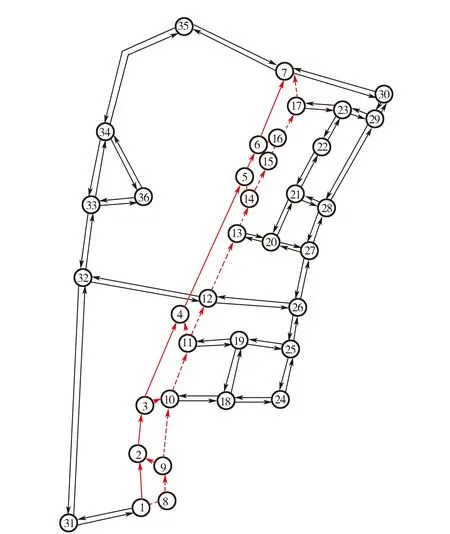
图8 三环快速路网示意图

4 算例分析

4.1 路网及基本参数设置

如图8所示，算例对象为成都市三环快速路草金立交至羊犀立交段、辅路和周边主次干道所组成的局域路网，节点编号1→2→3→4→5→6→7为快速路主线，虚线为辅路或匝道，其余实线为周边主次干道路网。路网的OD出行需求分为两部分：一是主线出行OD，主出行OD需求设置为饱和度0.8，起终点为1和7，主要研究将这部分出行需求分配到路网上；二是辅路和周边路网的出行需求，为研究不同路网状态下的可变限速控制效果，将辅路的饱和度设为0.5、0.7和0.9，周边路网的饱和度设为0.5。

在主线节点1→6之间共计5个基本段，设置5个限速区，节点6→7划分为两段，即瓶颈段前限速区和瓶颈段，共计6个限速区[12-13]。在每个限速区内划分元胞，元胞固定长度为222 m，从上游至瓶颈点共计25个元胞。设置共14个周期，200 s时主线下游路段7出现瓶颈，瓶颈在1 800 s后恢复，至2 800 s时仿真结束，控制周期为200 s,如图9所示。

图9 VSL控制子区示意图

4.2 Matlab求解结果

如表1所示，以辅路饱和度为0.5为例，对可变限速控制方案进行说明。经过6个周期后，路网达到均衡状态，并维持该限速值直至瓶颈恢复，车道数恢复正常，可变限速控制需要回调，经过1周期调整后，恢复正常并保持该限速值。利用MATLAB求解的可变限速建议值如图10所示[14-15]。

表1 可变限速控制方案持续周期数

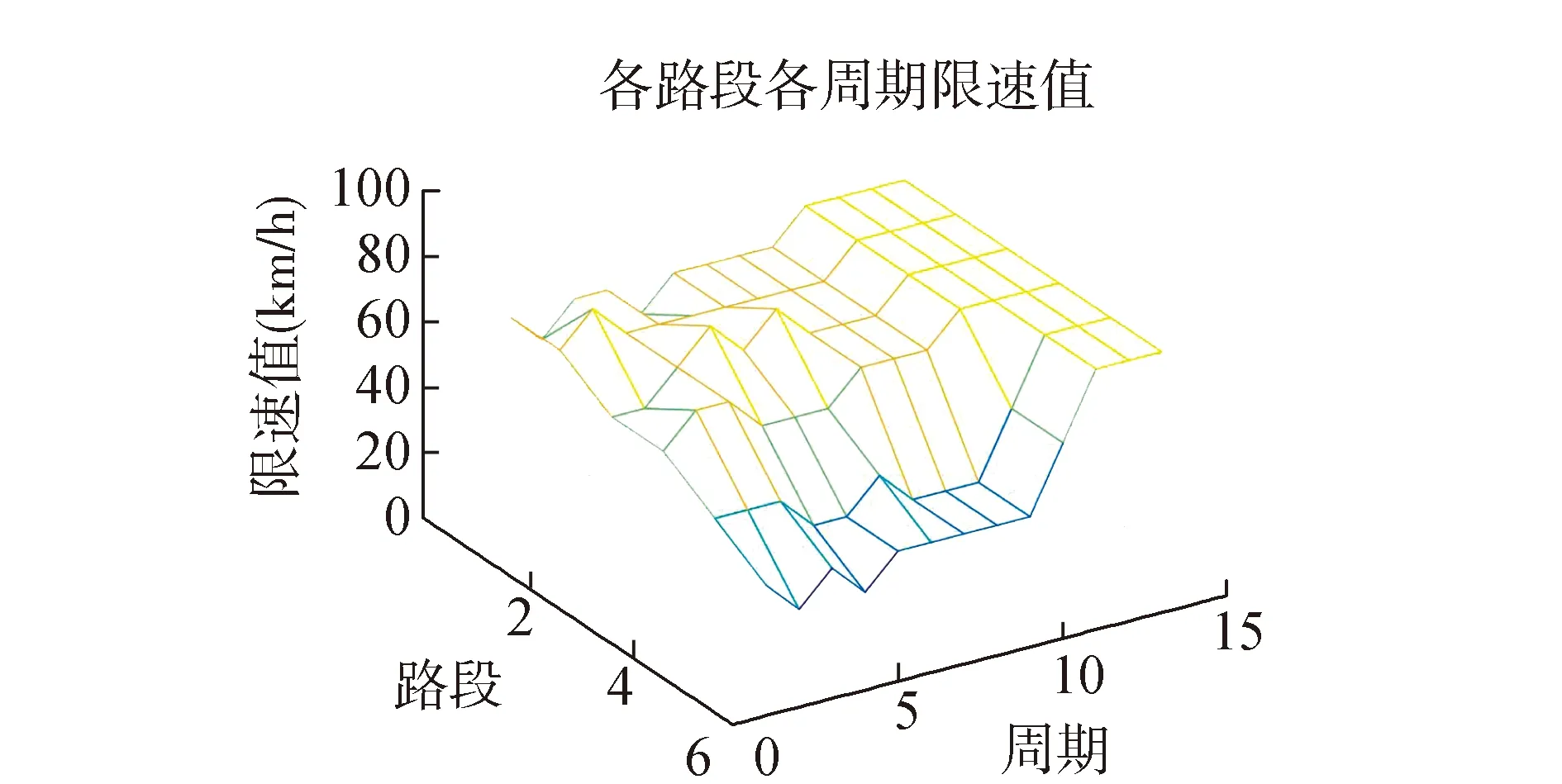
图10 辅路初始饱和度0.5下各路段限速值

4.3 VISSIM仿真结果分析

4.3.1 主线通行效率分析

为进一步验证模型有效性，将求解结果输入VISSIM中进行仿真实验。从表2中可以看出，在仿真时间内，辅路初始饱和度为0.5、0.7和0.9情况下，实行VSL控制后主线车辆总体行程时间均比无VSL下主线的行程时间低，降幅分别为8.5%、5.4%和2.6%。

表2 限速控制前、后下主线车辆总体行程时间

如图11所示，为VSL控制下主线各段的密度分布图，其中路段1为上游，路段6为下游。根据图11主线各段密度时空分布图，VSL控制能避免主线路段高密度区域的产生，从而有效减少主线的行程时间。

4.3.2 主线安全性分析

如图11所示，根据VISSIM输出的主线上游(路段1)至下游(路段6)的速度和密度数据，绘制出主线各段的速度和密度时空分布图[16]。与未实行可变限速控制的情况相比，可变限速控制下的交通流运行更加平滑，瓶颈区及上游速度突降现象得以缓解。

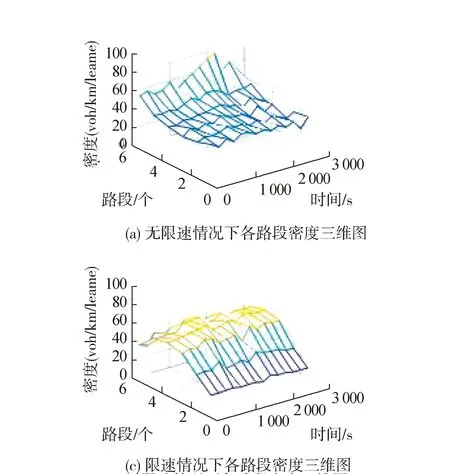
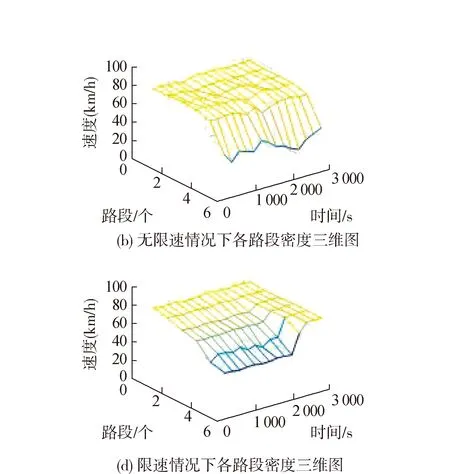
图11 无VSL和有VSL情况下主线各段密度、速度三维图(辅路饱和度为0.5)

5 结束语

本文以非常发性瓶颈区的交通特性入手，研究快速路基本段和瓶颈区交通流模型，并从通行效率和安全性两方面对元胞传输模型进行改进。进一步将研究对象从主线扩展到由主线、辅路和周边主次干道所组成的路网，研究可变限速值的设定对路网流量的调节作用。研究对象从单一的主线扩展到周围路网，以车辆总行程时间、相邻元胞内的速度差为优化目标，研究速度限制下的用户均衡，以此建立双层规划模型，设计出相应的算法，利用Matlab求解出限速控制方案和流量分配结果。最终，将结果输入到VISSIM中，结果表明，可变限速能有效提高非常发性瓶颈通行效率和安全性。