3500HP型钻井泵曲轴结构研究与优化

张洪生，田旭东

（兰州理工大学机电工程学院，甘肃兰州 730050）

随着现代钻井技术在工艺、水平方向的进步与发展，大功率钻井泵广泛应用于深井钻采、海洋钻井平台等石油钻采领域中[1]。钻井泵曲轴是传递力和转换运动形式的核心环节，也是连接齿轮传动机构与连杆机构的重要部件，曲轴在工作过程中受到周期性交变载荷与工作空间的限制，直接影响到钻井泵工作的稳定性、可靠性、噪声与使用寿命。因此，对曲轴模态特性分析以及曲轴结构轻量化设计的研究具有实际意义。

目前有限元分析是曲轴结构模态分析的主要方法，白稳乐等[2]通过对泥浆泵曲轴进行有限元计算与模态实验，研究泥浆泵曲轴结构在低阶频率下的振动形式与振动危险区域；朱洪其等[3]通过对高速压力机曲轴自由模态和约束模态的分析，提取出相应条件下前10阶模态参数，研究高速压力机曲轴在强迫振动下对下死点位移的影响。然而以上研究中对于曲轴机构动静态性能与质量的合理调配以及结构优化方案并未提出具体方案。

本文以3500HP 型钻井泵曲轴为研究对象，利用Solidworks 软件建立曲轴三维模型，并通过Ansys Workbench 有限元分析软件分析施加边界约束，提取曲轴模态。基于结构拓扑优化的理论，对钻井泵曲轴进行相应去除材料的改进与优化，在确保钻井泵曲轴静、动态特性的基础上，以满足曲轴结构轻量化设计的要求以及提升曲轴抑振性能的目的。

1 有限元模型的建立

1.1 曲轴有限元模型的建立

鉴于Ansys Workbench 分析软件在复杂结构三维模型建立的过程较为复杂。本文采用Solidworks三维建模软件进行钻井泵曲轴结构三维模型建立，并通过Solidworks 与Ansys Workbench 两个软件之间的无缝连接将曲轴模型导入，将数字化的CAD模型转化为参数化的有限元模型[4]。同时，为了避免模型当中小部分特征对于网格划分的影响，适当进行了相应的简化或修改如删除圆角，将螺纹孔改为通孔等。

3500HP型钻井泵曲轴是组装式锻铆结构曲轴，该结构由直轴、五个偏心曲拐及飞轮组成。偏心曲拐通过销连接与过盈装配的方式固结在直轴上，且每个曲拐之间相位角间隔144°分布。直轴材料选用40CrNiMoA，弹性模量209 GPa，泊松比0.295，密度为7.87×103kg/m3；曲拐材料选用 35CrMo，弹性模量207 GPa，泊松比0.286，密度为7.75×103kg/m3。鉴于钻井泵曲轴的复杂结构，选用六面体单元对各曲拐进行网格划分，选用四面体单元对直轴与飞轮进行网格划分。使曲轴结构不因网格划分过细，耗时过长，同时也使得主要配合部位划分精细得到精确解。经过反复调试，得出质量较好的网格划分，得出个56 504 节点，20 838个单元。曲轴结构的有限元模型如图1所示。

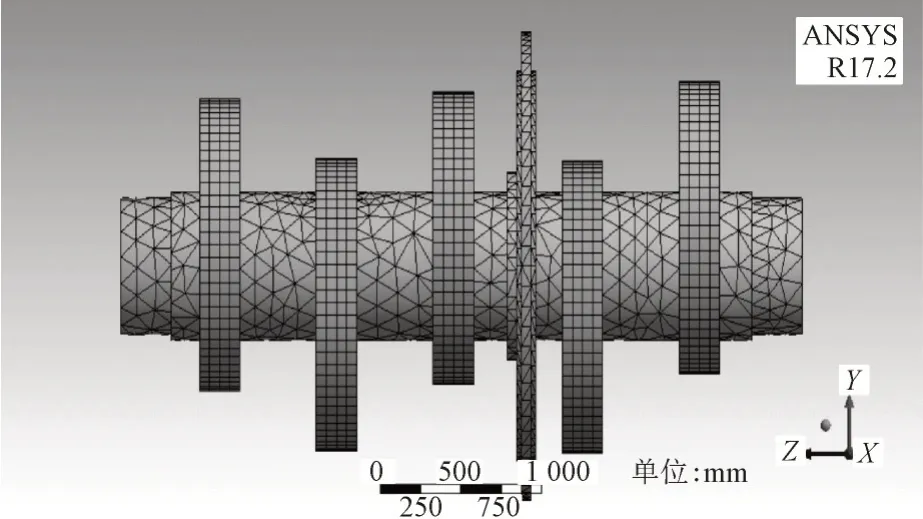
图1 曲轴结构有限元模型

1.2 有限元模态分析理论基础

有限元模态分析的本质就是对特征值、特征向量的求解，也可以称为模态提取[5]。钻井泵曲轴结构是一种无限自由度的复杂系统，动力学运动微分方程为

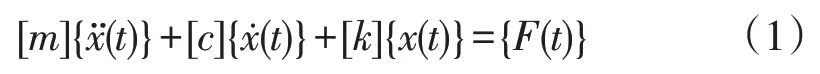
式中：{x(t)}、{x(t)}、{x¨(t)}分别为系统的位移向量、速度向量和加速度向量；{F（t）}为激振力向量，[k]、[c]、[m]分别为系统的刚度矩阵、阻尼矩阵和质量矩阵。

曲轴结构的自由模态是结构固有的振动特性，因此可视为一种多自由度无阻尼系统。动力学运动微分方程为

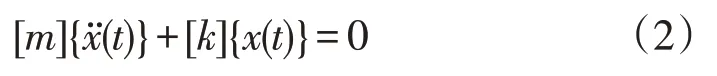
为求其模态向量，设

代入式（2）可得微分方程

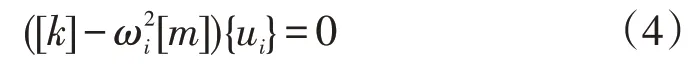
式中：{ui}为模态向量；f(t)为以时间为自变量的实函数；ωi为第i个振型的自然频率。

进而得出（4）式的特征方程：

通过求解该特征方程，可以得到n个自然频率，再代入（4）式，求得相应的解，即n个自然频率对应的模态向量[6-7]。

1.3 曲轴自由模态结果分析

自由模态分析主要针对结构在不受约束与外界载荷的条件下，计算结构本身固有振动特性的属性。本文通过利用有限元分析软件Ansys Workbench 中的模态分析模块对曲轴结构进行无边界约束自由模态的提取，以得到曲轴结构的固有频率和振型。由于前6阶固有频率接近0 Hz，为曲轴的刚体模态。因此，以第7阶模态作为曲轴的第1阶模态，得到前4阶固有频率和振型特征如表1所示，曲轴前4阶模态振型图如图2所示。

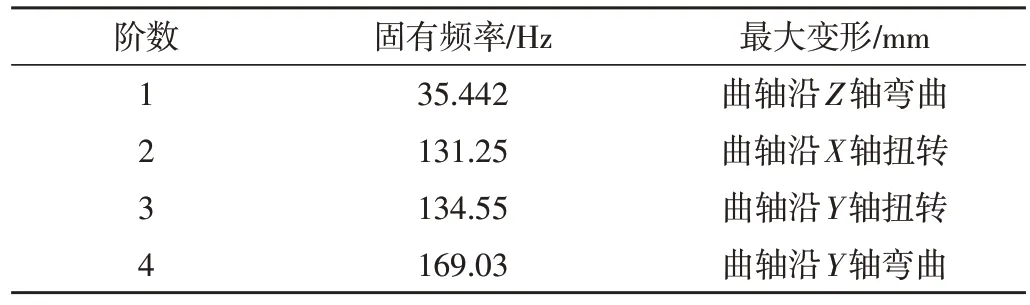
表1 曲轴的前4阶模态分析结果

根据图2 曲轴前4 阶模态振型图可直观观测曲轴各阶振型变化情况可知，曲轴右端沿Z轴反向的弯曲振动是第一阶振型主要表现形式；曲轴沿X轴的扭转振动是第二阶振型主要表现形式；曲轴沿Y轴的扭转振动是第三阶振型主要表现形式；曲轴沿Y轴的弯曲振动是第四阶振型主要表现形式。且综合表1曲轴前6阶自然模态的分析结果可知，曲轴的基频为35.442 Hz，满足钻井泵曲轴结构理论频率。但考虑到正常工况下对曲轴减振降噪的更高要求，低阶固有频率的提升仍存在空间，故对其进行结构优化设计。

2 曲轴的结构拓扑优化设计

2.1 拓扑优化理论基础

拓扑优化是继尺寸优化、形状优化之后的一种新兴的结构优化方法，同时也随着有限元分析技术发展逐渐成熟[8]。与尺寸优化与形状优化对比，拓扑优化在节省材料，降低质量，提升结构力学性能方面更有效可行，旨在满足外界载荷和边界约束等条件下，在给定设计域内寻求材料和形状的最优分布，以得到新型拓扑结构，实现最优设计方案。拓扑优化通常以材料密度作为载体，根据约束条件对目标函数进行优化，因此，设计变量、目标函数以及约束条件是拓扑优化的核心要素。目前连续体结构最为常用的拓扑优化方法为变密度法，变密度法通过设定一种密度在0～1 变化的假想材料代替各向同性材料，并用连续变量的密度函数来研究设计域内对应关系[9-11]。变密度法经常应用的插值类型主要有SIMP 模型和RAMP 模型两种，这两种计算方法均通过设立惩罚函数对处于0～1中间密度进行惩罚，使其归于0 或1 的两种单元密度。这样不会引起结构刚度矩阵的变化，同时对结构的动态性能影响较小。

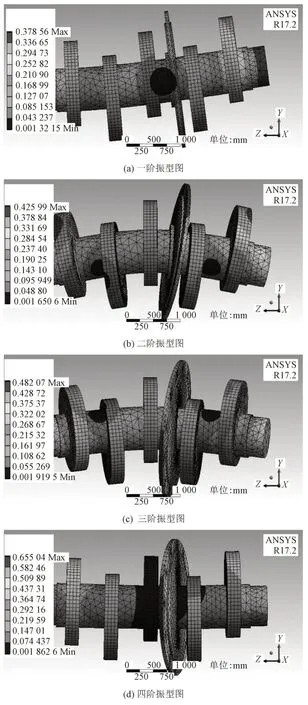
图2 曲轴前4阶模态振型图

2.2 曲轴拓扑结果分析与结构改进

现基于之前曲轴有限元分析过程中的网格划分模型及相应的边界条件等数据，利用Ansys Workbench有限元分析软件中的Shape Optimization 拓扑优化模块，以质量减轻20%为目标进行优化。得出的拓扑优结果如图3所示。

结合拓扑优化结果、曲轴结构特点与动态性能分析可知，图3 中建议保留的部分为浅灰色区域显示，建议材料去除部分为深灰色区域显示。结构弯曲、扭转主要发生在曲轴结构的中间部位，且深灰色区域主要分布在偏心曲拐、飞轮两侧以及直轴中间部分，可知曲轴结构仍存在部分材料冗余，具有较大改善空间。因此根据实际情况，采用在5 个偏心曲拐、飞轮上开对称孔的材料去除方案，优化后的曲轴结构如图4 所示。

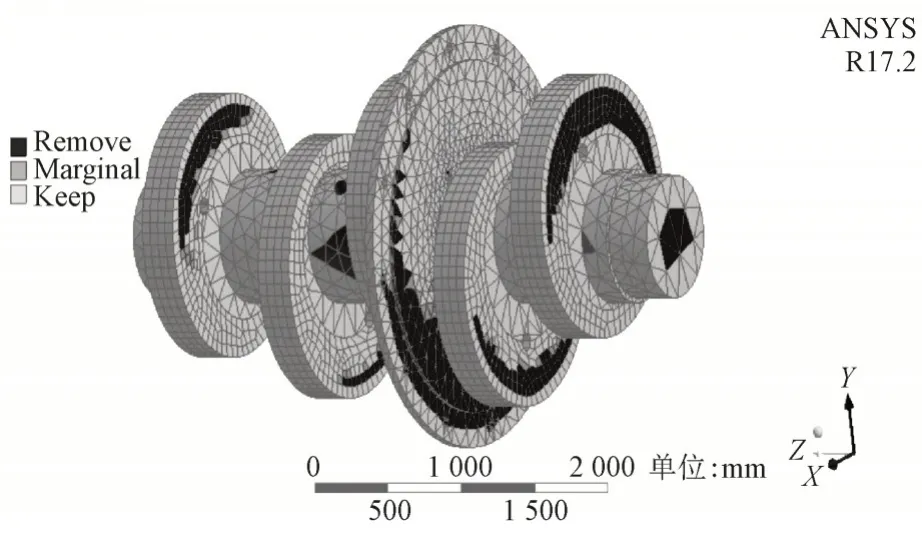
图3 拓扑优化结果

图4 优化后的曲轴结构图

2.3 对拓扑优化结果的验证

按照相同的工况，对改进后的曲轴结构重新进行模态提取，所得改进后曲轴前4阶模态振型图如图5所示。观察所得，改进后曲轴的第一阶模态为36.763 Hz，与改进前相比提升了3.73%。同时，曲轴结构整体质量减轻了7.55%，实现曲轴轻量化的要求。与改进前的分析结果对比结果如表2所示。

表2 优化前后结果分析

图5 改进后曲轴前4阶模态振型图

3 结 论

本文以某型号钻井泵曲轴作为研究对象，利用Ansys Workbench 分析软件对其进行模态提取。针对曲轴结构典型工况下材料冗余部位选用拓扑优化分析方法进行优化改进，并对优化后的曲轴结构重新分析，在质量、低阶固有频率方面加以对比。结果表明，优化后的曲轴结构质量降低了7.55%，一阶固有频率提升3.73%，二阶固有频率提升3.43%，实现曲轴结构轻量化，同时也改善了结构的动态特性，为曲轴结构优化设计进一步的理论研究提供理论依据。