高考中数学的内综与外联

蒋红瑛

（四川职业技术学院 应用数学与经济系，四川 遂宁 629000）

基础教育课程改革近十年，在数学教学中，要求教师以课标为纲，创造性地使用教材，即用教材教而不是教教材.而新教材更注重数学知识的综合性和适用性的学习，这就要求第一，数学教育者认真研究数学各分支之间的相互作用，优化数学问题的求解；第二，认真研究数学与自然科学和社会科学，如物理、地理、化学、生物等学科的相互联系和作用；第三，认真研究生产、生活实际中出现的问题，将它们用数学建模的方式转化为数学问题，再用数学的方法使其得以解决.

那么，数学教师在教学过程中就应将这三个方面的知识方法充分展示给学生，让他们养成自觉联系的习惯.有了教师的用心引导，在师生合作、共建下，学生在学习过程中必然会主动建构知识，从而达到培养学生的创新精神，提高学生的创新能力的教育目的.

1 加强数学各分支之间的综合运用，优化数学问题的求解

尽管新教材将传统的数学学习内容进行了充实、调整、更新和重组，注重了基础性、层次性和发展性，但课后的习题基本上是用刚学的知识和分支内的知识来解决，很少用其它分支的知识来解决数学问题.数学报刊杂志和课外参考资料在综合运用各分支的知识来解决数学问题时，研究的方法很多很多，可学生没机会，也没太多的时间去看这些资料，这就需要我们教师多学习、多研究、多总结，在教学中多渗透应用，充分展示数学各分支的相容性、互补性、和谐性，培养学生灵活运用各分支的知识来解决数学问题的习惯，扩展学生的思维，增强解题的敏捷性和准确性，让数学在学生心目中生动、形象而高大起来.用以下两道今年的高考题来说明这个问题.

例1（19福建理第16题）己知等比数列{an}的公比q=3，前三项和S3=，

（1）求数列{}an的通项公式；

（2）若函数f(x)=Asin(2x+φ)(A＞0,0＜φ＜π)在x=处取得最大值为a3，求函数f(x)的解析式.

解析：该题属于数列问题，但它综合考查等比数列、三角函数、方程思想，因此，我们必须熟练掌握这几方面知识之间的相互关系，灵活求解答案.

解：（1）由q=3,S3=得=,解得a1=，所以an=3n-2.

（2）由（1）知a3=3，因为函数最大值为3，所以A=3，

又因当x=时f(x)取得最大值，所以

又 0＜φ＜π,故φ=，所以

例2（19年全国卷Ⅰ理第19题）已知抛物线C：y2=3x的焦点为F，斜率的直线l与C的交点为A，B，与x轴的交点为P.

（1）若|AF|+|BF|=4，求l的方程；（2）若,求||AB

解析：本题考查抛物线的几何性质、直线与抛物线的综合应用问题，但还必须熟习平面向量、弦长公式的知识，综合应用其相关知识，才能完成此题.

解：（1）设直线l方程：y=x+m,A(x1,y1),B(x2,y2).

由抛物线焦半径公式可知|AF|+|BF|=x1+x2+=4,∴x1+x2=，

∴x1+x2==，解得：m=-

∴直线l的方程为：12x-8y-7=0.

（2）设P( )

t,0,则可设直线l的方程为

∴y1+y2=2,y1y2=-3t.

2 深化数学在生产、生活中的综合运用，培养学生的创新精神和实践能力[1]

数学中有很多知识与生产、生活实际相联系，并需用数学知识来解决的现实问题，这就充分体现了数学的工具性、通用性的作用.近几年高考在银行利息、个人所得税、商品优惠、最优化问题、弹道曲线、天体运行轨道等方面作了很好的导向，加大了数学在生产、生活中的运用的考查力度.因此，我们必须在课堂教学中加强数学知识与生活实际的紧密联系，把枯燥无味的数学问题附以生活背景，使其具有生命力，让学生在实践中自主、自悟、自得，对生活中的实际应用问题能用数学化的思想去思考分析信息、处理信息，最后解决问题.从而让学生深深感知；“数学来源于生活，数学也服务于生活”.这样，学生在平时的学习中就会在思想上自觉注重知识积累，掌握常见数学模型的构建，抓住函数、不等式、数列等重点内容，重点突破.打破高考题高不可攀的心理障碍，相信自己的实力，能冷静分析所给问题的条件和所求，联系相关学科的概念和原理，抓住题干中的数与量的关系，将实际生活问题转化为熟悉的数学问题，应用所学的数学知识和方法解决这些现实问题.

有关这方面的例子很多，如四川高考题中16年的居民用水问题、17年的超市销售问题、18年的工厂生产效率问题、19年的药品治疗问题等等，这些都是很好的范例，下面举17年的超市销售一例说明这个问题.

例3（2017年全国高考文卷III第18题）某万达超市计划按月订购一种可乐，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的可乐降价处理，以每瓶2元的价格当天全部处理完.根据历年年销售经验，每天需求量与当天最高气温（单位：℃）有关.如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶.为了确定七月份的订购计划，统计了前三年七月份各天的最高气温数据，得下面的频数分布表：

?

以最高气温位于各区间的频率代替最高气温位于该区间的概率.

（1）七月份这种可乐一天的需求量X（单位：瓶）的分布列；

（2）七份一天销售这种可乐的利润为Y（单位：元），当七月份这种可乐一天的进货量n（单位：瓶）为多少时，Y的数学期望达到最大值？[2]

解析：此题考查离散型随机变量的分布列及其数学期望.通过认真阅读题意，明确题中的生活情境，确定与相应数学知识相衔接而建立数学模型，让学生深刻体会到：“数学来源于生活，数学也服务于生活”，从而培养学生的实践能力和创新能力.

解：（1）根据题意，七月份这种可乐一天的需求量X的可能值为200、300、500，

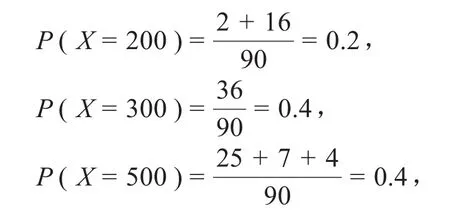
所以X的分布列为：

500 0.4 X P 200 0.2 300 0.4

（2）①当n≤200时，Y=n(6 -4)=2n，所以E(Y)=Y×1=2n≤400.

②当200＜n≤300时，若X=200，

则Y=200×(6 -4)+(n-200)(2 -4)=800-2n.

若X≥300，则Y=n(6 -4)=2n.

所以E(Y)=P(X=200)×(8 00-2n)+P(X≥300)×2n=160+1.2n.

因为200＜n≤300，所以此时E(Y)∈(4 00,520].

当300＜n≤500时与n＞500时的解答过程与②类同，此处略去.

综上可得当时n=300，即七月份这种可乐一天的进货量为300瓶时，Y的数学期望最大，最大值为520元.

3 强化数学与相关学科的联系，突出数学在其它学科中的核心作用

众所周知，数学在学校教学中是一门基础学科，也是一门工具学科，它贯穿了所有的自然学科，任何一门自然学科的研究都不能脱离数学而自由存在.数学作为一种思维和方法的工具，它在科学研究的领域中也具有非常重要的地位.在新课标教材和近几年的高考中，都出了数学与其它学科相关联的题例.作为数学教师，为了进一步完善数学的教学，必须自觉学习和理解其它学科的概念和规律，必须在教学过程中灵活运用其它学科的知识来分析和解决相关的问题，这样才能使数学的学习达到更新的境界，才能使学生适应当前的高考需要，才能更全面地提高学生的素质，达到以培养创新精神和提高实践能力的目的，以下举几例加以说明这个问题.

例4（19年全国高考理卷II第4题）2019年1月3日，著名的“嫦娥四号”探测器成功实现人类历史上首次月球背面软着陆，从而使我国航天事业取得了又一重大成就.实现月球背面软着路需要解决的一个关键而重要的技术问题就是地面与探测器的通讯联系.我们国家为解决这个问题，发射了嫦娥四号中继星“鹊桥”，鹊桥沿着围绕地球月拉格朗日L2点的轨道运行，L2点是平衡点，位于地月连线的延长线上.设地球的质量为M1，月球质量为M2，地月距离为R，L2点到月球的距离为r，根据牛顿运动定律和万有引力定律，r满足方程设α=，由于α的值很小，所以在近似计算中则r的近似值为（ ）

解析：此题表面上看它是一个物理问题，涉及物理上的术语，通过分析，抓住α=

这个条件，转化为函数模型，利用函数相关知识即可求解.

解：由α=可知r=Rα，代入，即可得那么，得：故正确答案为D.

例5（19年全国卷I理4题）古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚

著名的“断臂维纳斯”便是如此.此外，最美人体的头顶至咽喉的

若某人满足上述两个黄金分割比例，且腿长为105cm，头顶至脖子

下端的长度为26cm，则其身高可能是[ ]

A.165cm B.175cm C.185cm D.190cm

解析：这道“断臂维纳斯”考题以美学为背景设计，情境贴近实际，考查的是黄金分割的计算.题目新颖，之前没有出过此类题目，导致考生在考试的时候一脸懵，下考场后，甚至有学生觉得“简直噩梦”.实际上这类题目都是纸老虎，只是要学会转化，化未知为已知，化陌生为熟悉，要知道高考试卷除了考查考生知识的掌握度，还有就是考生是否能够将学到的知识举一反三，和随机应变.

将头顶到咽喉的长度表示为a，咽喉到肚脐的长度表示为b，肚脐到足底的长度表示为c，头顶到肚脐的长度表示为d.

大家又认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是

又d=a+b＜26+42=68，而c=

而己知c＞105，又d=c×0.618＞65，

105+65＜c+d＜110+68，即170＜c+d＜178.

故正确答案是B.

例6（18年北京高考理第4题）“十二平均律”是以前通用的音律体系，明代朱载堉是第一个用数学方法计算出半音比例，他为这个理论的发展做出了突出的贡献.十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于若第一个单音的频率为f，则第八个单音的频率为

解析：此题以“东方文艺复兴式的圣人”朱载堉的科学艺术“十二平均律”为背景，体现了出题者向考生传达我国古代科技成就，引导学生体会中国古代先贤在人类文明中的贡献，有利于增强文化自信与民族自豪感.这是一道音乐、数学和物理学相结合的考题，渗透了数学史和数学文化，把数学应用于音乐艺术上，让学生感悟数学的美感.

由等比数列的定义，不难知道每一个单音的频率是成等比数列，因此，根据等比数列的相关性质容易得解.

由题意可知，单音的频率构成以a1=f为首项，q=为公比的等比数列，则a8=a1q7=()7f=f，故选择答案D.

总而言之，通过这三方面的论述，我们可以看到数学知识和方法在其他相关学科及其现实生活中的重要地位，真实反映了数学应用的广泛领域，更充分体现了数学的应用价值.作为数学教师就必须研究数学各分支间的内存联系和相互作用；必须关注科技和生活中的实际问题，用数学的眼光去提炼、去抽象、去探寻其内在变化关系，进而解决实际问题；必须去学习其它自然学科的知识，运用数学的观点和方法，采用综合的手段解决各种各样的数学型问题；还必须将上述观点运用到教学过程中，去激发学生学习数学的热情，增强学生对数学价值的认识，逐步提升学生的数学素养，从而达到培养学生的创新精神和实践能力的目的，使数学这门学科不管是在学生自身综合发展中，还是在“3+综合”、将来的“3+3”或“3+1+2”高考中，展现出它璀璨耀眼的一面.