非线性时间分数阶Gardner方程新精确解的构建

黄 春,张 佳

（1.四川职业技术学院 应用数学与经济系,四川 遂宁 629000；2.四川托普信息技术职业学院 思政部，四川 成都 611743）

1 预备知识

非线性分数阶微分方程具有广阔的应用领域和纵深的发展前景,因此求其精确解具有重要的理论意义和实用价值,研究者们对此做了大量工作,并提出和发展许多有效的求解方法,主要包括:分数Riccati映射法[1],分数首次积分法[2],分数指数函数法[3],分数(G'/G)-展开法[4]等.

非线性时间分数阶Gardner方程[5-6]:

其中:0≤x≤1,t＞0,0＜α≤1,是Jumarie[7]修正的Riemann-Liouville分数阶导数.

Jumarie修正的Riemann-Liouville分数阶导数:

Jumarie修正的Riemann-Liouville分数阶导数性质:

Gardner方程在等离子体物理、流体力学和量子场理论中都有重要的应用.整数阶Gardner方程也称KdV-mkdv方程,可以用反散射法和Hirota双线性法,达布变换法,(G'/G)-展开法等求解.文献[5-6]中分别用F-展开法、q-HAM分析法对时间分数阶Gardner方程进行研究并获得其Jacobi椭圆函数解,解析解.本文拟用修正的Riemann-Liouville分数阶导数结合扩展的(G'/G)-展开法构建方程新精确解.

2 方法简述

考虑下面的非线性分数阶微分方程：

其中是未知函数u=u(x,t)关于自变量x和t的Jumarie修正的Riemann-Liouville分数阶导数,P是关于u及其偏导数的多项式.

步骤1作分数阶复变换

方程(4)转化为只含变量ξ的整数阶常微分方程

步骤2 假设方程(6)的解可以表示成关于(G'/G)多项式的形式

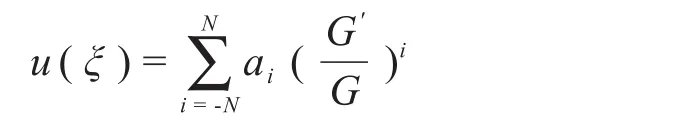
其中G=G(ξ)满足辅助方程

计算(7)式可得:

其中λ,μ为待定常数.正整数N可以通过齐次平衡原则确定.

步骤3 合并(6)式中(G'/G)的相同幂次项,令(G'/G)的各次幂系数为零,导出关于ai(i=-N...0...N)为未知量代数方程组,并求其解,从而得出方程(4)的精确解.

3 运用与结果

首先对方程(1)作复变换

得到常微分方程,积分一次,令积分常数为0,得

平衡最高阶导数项u3和非线性u'',则有:3N=N+2,有N=1,则

将u,u2,u3,u''代入方程(10)中,得到关于a-1,a0,a1的代数方程组:

解上述代数方程组可得:

情形1 当＞0时,方程(1)有如下形式的双曲函数解:

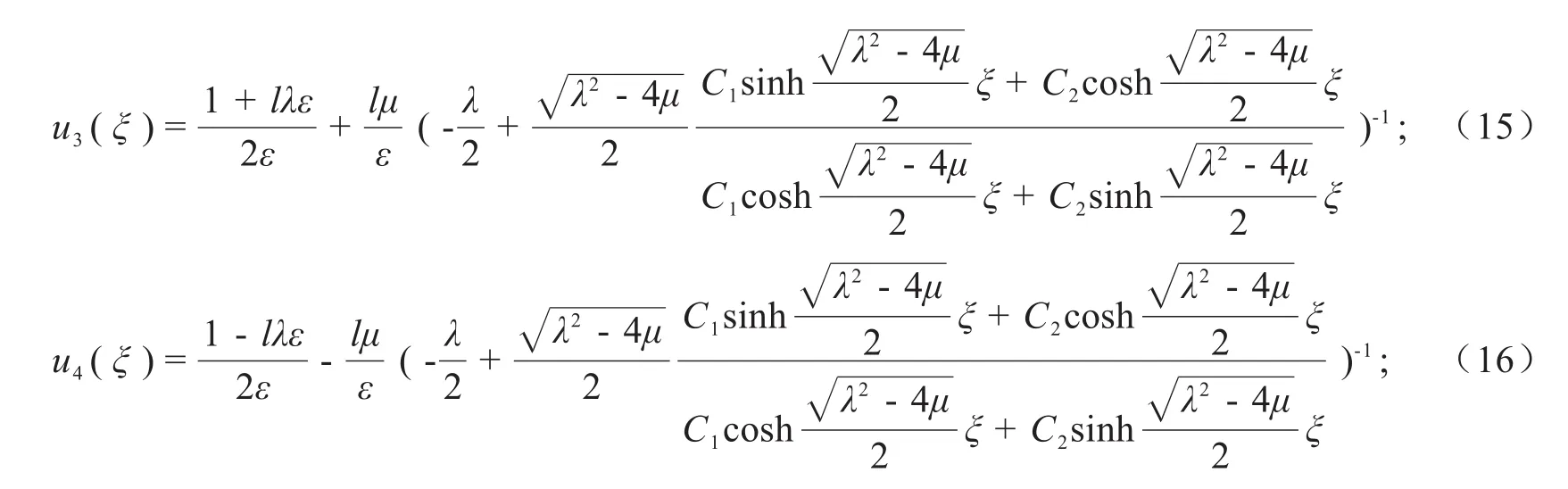
其中ξ=lx+C1,C2为任意常数.

情形2 当＜0时,方程(1)有如下形式的三角函数解:

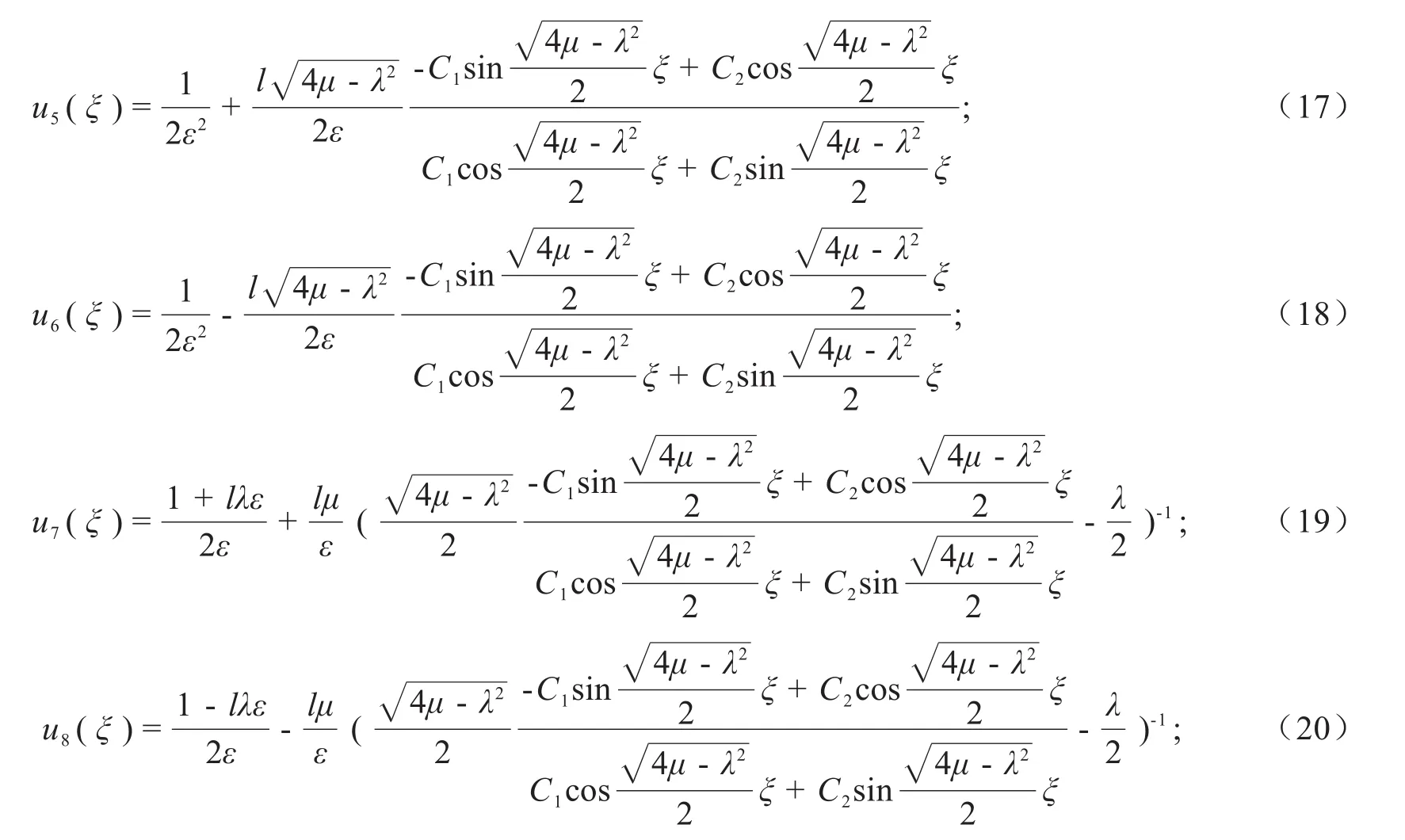
其中ξ=lx+C1,C2为任意常数.

情形3 当=0时,方程(1)有如下形式的有理函数解:

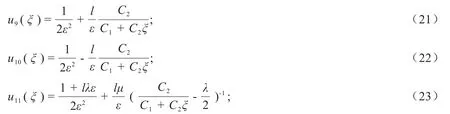
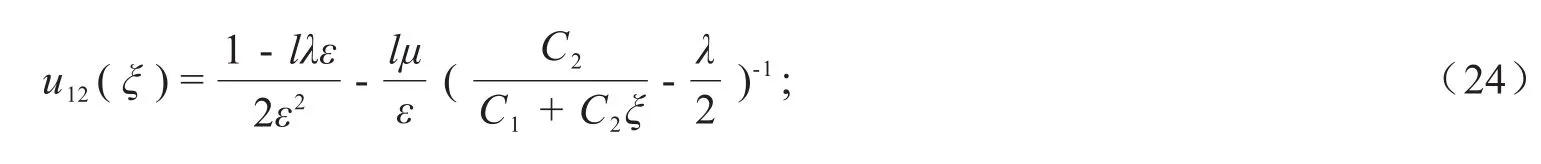
其中ξ=lx+C1,C2为任意常数.

4 结论

文中借助修正的Riemann-Liouville分数阶导数结合扩展的(G'/G)-展开法构建非线性时间分数阶Gardner方程的新精确解,其中包括为含参数的双曲函数解,三角函数解,有理数解,这些解在以往文献中未曾出现.这些解对于理解复杂的非线性物理现象和分数阶微分方程的原理很有帮助,可见该方法简洁,高效,是求解一类非线性分数阶微分方程行之有效的方法.