基于全变差模型的自适应参数选择方法

魏海广，赵 玉，卢立玄，张 涛

(安徽工业大学数理科学与工程学院，安徽马鞍山243032)

对含噪声的图像进行去噪处理一直是图像处理领域的热点和难点之一。在图像去噪中，要保留图像的边缘、纹理等细节信息，以保证修复后的图像与原图像有一定的结构相似性。为此，许多专家学者提出了相关理论和方法，在边缘保护方面，Rudin等[1]从能量极小化的角度出发，将全变差半范数作为正则项引入到图像去噪模型中，建立了全变差正则化模型(简称ROF模型)，该模型通过引入能量泛函，将图像去噪问题转变为求能量泛函最小问题，在保护图像边缘上取得了良好的效果；在纹理保护方面，Meyer等[2]提出TV-G模型，将图像分解为几何部分和纹理部分，Buades等[3]提出非局部均值算法，利用像素之间的距离来表示相似度，取得了较好的效果；在数值求解方面，对偶投影算法、ADMM交替方向乘子法[4]、Bregman迭代法[5]等都能达到快速收敛，易于数值实现。

ROF模型中的能量泛函分为逼近项和正则项两部分。其中：逼近项用于去除噪声，保证去噪后的图像与原图像的相似性；正则项则防止去噪过强，起到抑制噪声的作用。因此，需要选取适当的权重参数用于平衡这两项的关系[6]。目前，国内外已有学者提出了一些权重确定方法，如无偏预测风险估计器[7](URPE)，局部方差估计[8]，基于Morozov偏差原理[9]选取参数等。本文基于全变差正则化模型[10-11]，利用Chambolle对偶投影算法[12-14]，提出一种参数可随着迭代算法自适应改变的新方法，该方法根据图像的先验信息，能够自适应地选取合适的参数，进而保证去噪后的图像能够保留更多的细节信息。

1 模型的建立

ROF模型的基本思想是将图像处理问题看成一个能量系统，其中：不含噪声的图像能量相对较小；当图像被噪声污染后，图像变得不光滑，其能量相应地增大了。通过这种思想，将图像去噪问题转化成一个能量最小化问题，再通过变分法进行求解，模型如下

其中：E(u)表示图像的能量；u 为去噪后的图像；BV 表示有界变差函数空间；‖ ‖· 表示L2范数；f 表示观测图像；λ 表示正则化参数；J(u)=∫Ω|∇u(x)|dx，∇表示梯度算子。模型的第一项为正则项，第二项为逼近项。令图像数据表示为一个N×M 的二维矩阵(i 表示矩阵行，j 表示矩阵列)，X 表示欧几里得空间，为了定义离散的全变差范数，先给出正则项中离散梯度算子的定义。梯度∇u 是一个在Y=X×X 的向量，表示为

其中：i=1,2,…,N；j=1,2,…,M。

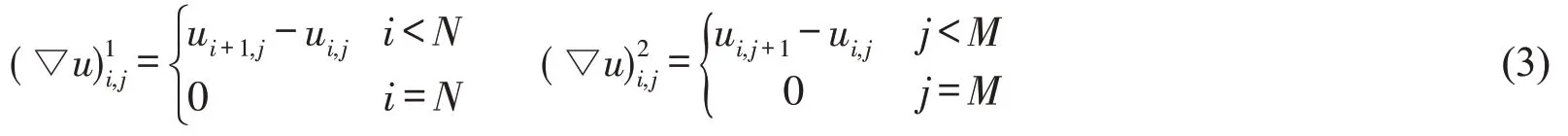
能量泛函式(1)中的j 是一阶齐次的，即对任意的u 和λ ＞0，都有J(λu)=λJ(u)，，在凸分析和凸优化问题中可以得到。

由Legendre-Fenchel变换

其中，u,vX=。对于闭凸集K，J*为示性函数[15]

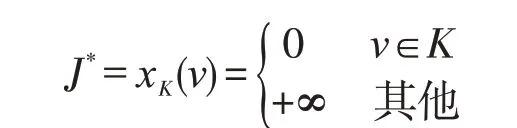
2 模型的求解

2.1 投影算法

最小化能量泛函模型

其中，f ∈X，λ ＞0，‖ ‖u2= u,uX，该模型表达式的欧拉-拉格朗日方程为0 ∈u-f+λ∂J(u)。其中，∂J 表示次微分，定义为w ∈∂J(u)⇔J(u)≥J(u)+ w,v-uX，对于任意的v，欧拉-拉格朗日方程式可以表示为(f-u)/λ ∈∂J(u)，等价于u ∈∂J*((f-u)/λ)，再经变形可得

令w=(f-u)/λ，则式(6)可写成

式(7)是式(8)泛函的欧拉-拉格朗日方程

因此，w=(f-u)/λ 是该式的极小值，J*由式(4)给出，若PKλ表示在集合K 上的投影，得模型的解为

散度算子div表示为

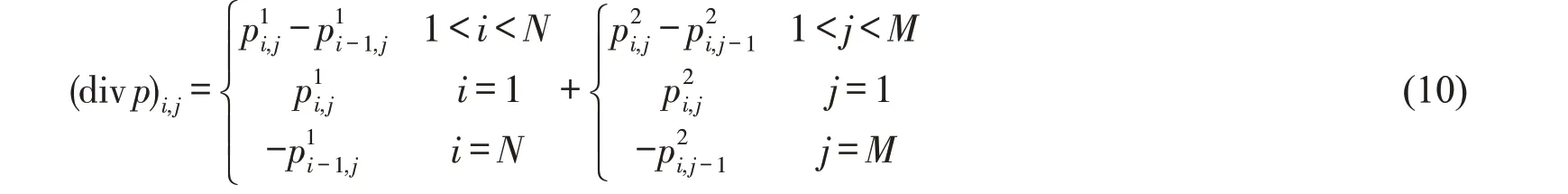
这样，将计算u 的问题转化成了计算非线性算子PKλ问题。非线性投影算子的计算等价于求解于下列问题

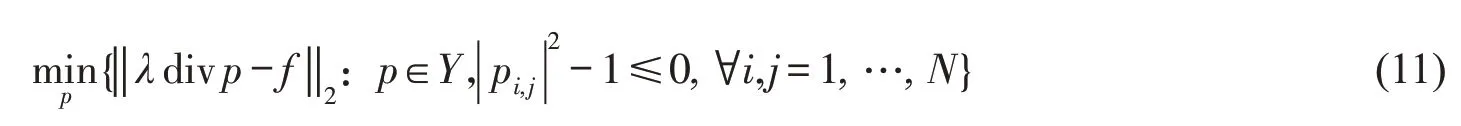
在KKT条件[8]下，存在拉格朗日乘子αi,j≥0，满足

结合梯度下降算法，取τ ＞0，p0=0，对任意n ≥0，有

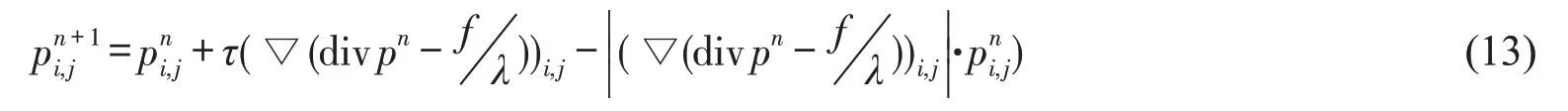
整理得

2.2 自适应参数的选取

ROF模型中处理后的图像与原图相比都存在不同程度的模糊，图像清晰度下降。原因在于求解模型的算法中选取的正则项参数是固定的，不能随着迭代算法进行自适应地改变。若选取的参数过大，去噪程度过强，则会导致处理后的图像过于光滑，不能保护纹理边缘等细节部分；若选取的参数过小，去噪程度低，不能达到去噪效果，进而影响算法的准确性。

文中通过构建正则项、逼近项和结构相似性之间的函数关系式，使模型参数能够随着迭代的进行自适应地选取合理值。能量泛函表达式为

则项是唯一确定的，因此可以构造权重r(λ)关于正则项和逼近项的函数关系为

式中w 为调节参数。由式(16)权衡正则项和逼近项之间的平衡关系。在迭代过程中，r(λ)=0，根据不动点迭代原理，权重更新准则[16-17]为

其中，每一次权重λn+1的取值都是由上一次迭代出的正则项J(uλn)和逼近项E0(uλn)两者决定。文中通过测试不同图像在不同噪声强度下的数据，采用多元线性回归拟合的方法拟合出参数w 与权重λ，结构相似性SSIM，正则项E 和逼近项J 之间的函数关系式，使得参数w 在迭代过程中随着权重λ 的迭代而选择不同的值，部分测试数据如表1。

根据多元线性回归模型，拟合出参数w 的函数关系式，结果如表2。

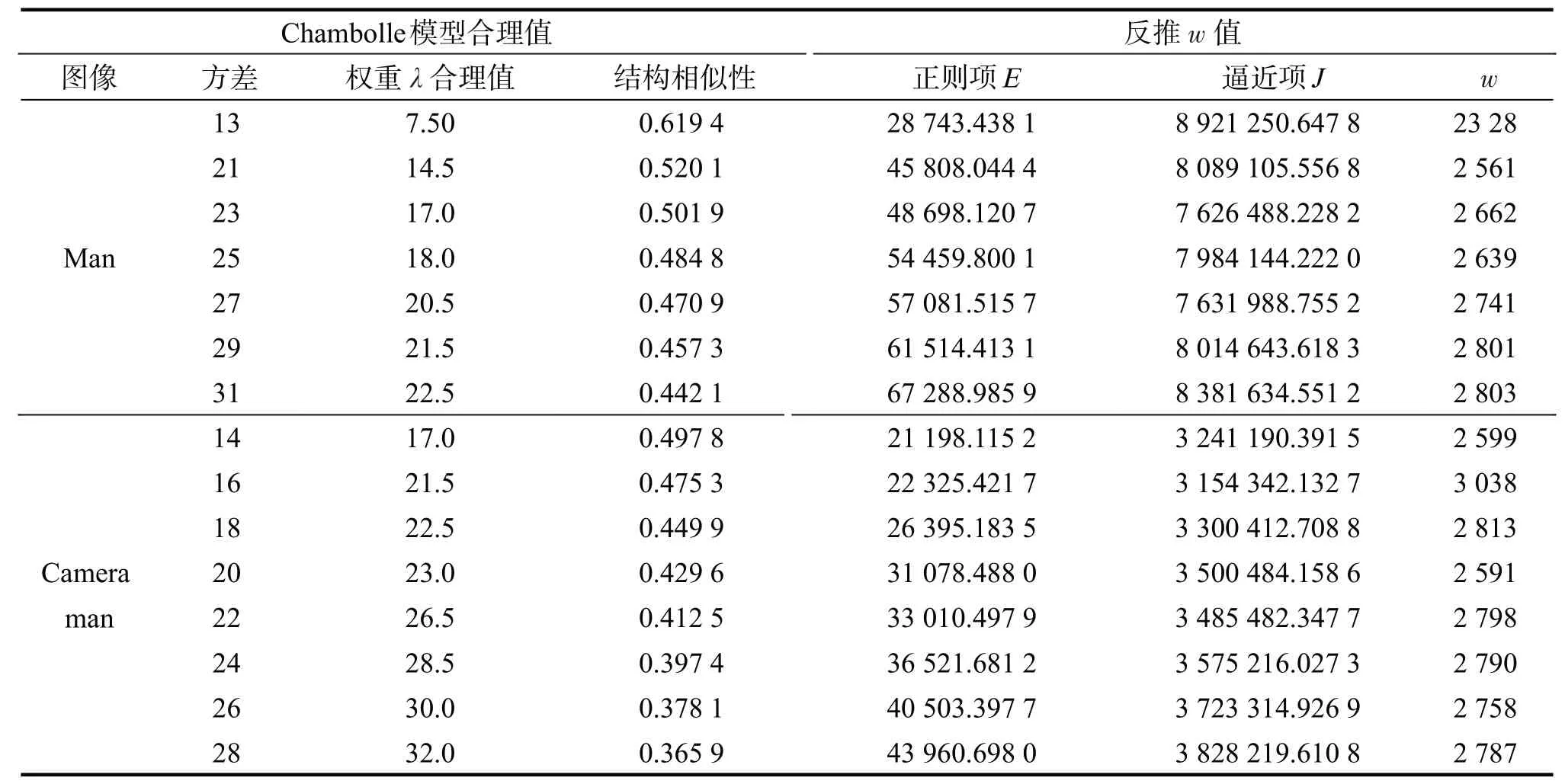
表1 测试实验数据Tab.1 Experimentaltest data

表2 拟合系数Tab.2 Fitting coefficients

即模型的函数关系式为

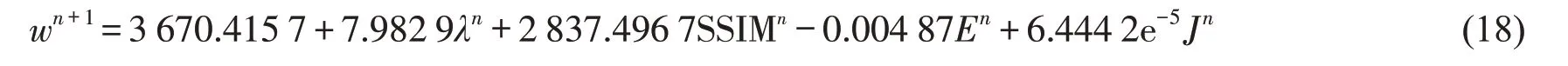
回归系数的95%的置信区间估计见表3。由表3可看出该线性拟合中F检验的P值为1.317 2e-17，远远小于0.01，通过了显著性检验，说明该拟合模型是有效的。

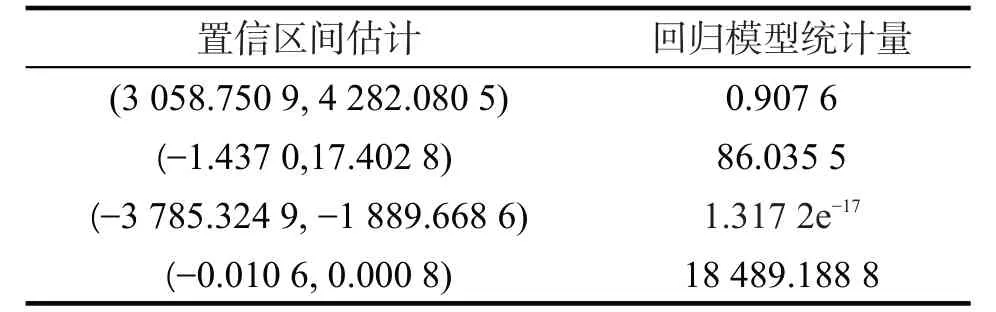
表3 拟合模型检验值Tab.3 Test value of fitting model

2.3 算法流程

步骤1 初始化：λ,w,n

步骤2 1)根据λ div p 算出投影算子，

E=‖ ‖u-f2/(2λ)算出逼近项；

2)得到去噪后图像u，算出u 的梯度、正则项数值和结构相似性；

3)根据w 的拟合公式(式(18))，算出w；

4)根据w，算出λ 值；

5)令n=n+1，将λ 代入1)，再次循环。步骤3 输出u，结束。

3 数值实验与分析

选用4幅灰度级为0～255的256×256的图像，分别利用Chambolle对偶投影方法[9-10]和本文提出的自适应对偶投影方法进行验证，同时在结构相似性、峰值信噪比等方面进行对比和分析，见图1。

图1 去噪效果图Fig.1 Denoising effect images

由图1可看出，无论对于高斯白噪声还是泊松噪声，实验后的图像效果要比噪声图像清晰很多，说明了算法改进的可行性。每组实验的图像相似结构性SSIM和峰值信噪比PSNR，分别和Chambolle合理值进行对比。Chambolle 合理值的获得，是通过人工测试调整，在图像取不同参数时算出此时图像的结构相似性SSIM和峰值信噪比PSNR。当这两个指标最大时，同时参考主观上对图像去噪的视觉效果，将此时的SSIM和PSNR数值视为Chambolle算法的合理值，结果如图2。从图2可以看出，当图像方差较小时，图像Man经该算法处理后的结构相似性和合理值相比有些差距，但相差是比较小的，当噪声方差大于25时，经过改进后算法结构相似性与合理值比较吻合。图像Camera man则无论噪声方差大小，经本文算法处理后其结构相似性和峰值信噪比都与合理值几乎重合，吻合度较高，从而进一步说明了改进后算法的合理性和可行性。从图像Camera man实验效果图来看，无论是对于高斯白噪声还是泊松噪声，经该算法去噪后的效果较好，在图像纹理和细节部分也能够较好的保护，避免了由于原算法中权重的主观选取而导致图像过于光滑和去噪不彻底的弊端，同时，算出了每组实验的峰值信噪比与合理值进行对比，结果如图3。从图3可以看出，改进算法后的图像Man峰值信噪比与合理值相差较小，从总体上看，相差的数值也相对较小。图像Camera man的峰值信噪比与合理值很接近，几乎重合，其去噪效果较好。

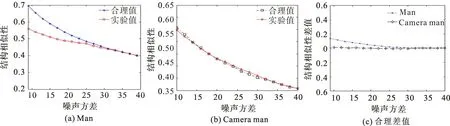
图2 图像Man和Camea man的结构相似性及其合理差值Fig.2 SSIM and their resonable difference of image Man and Camea man

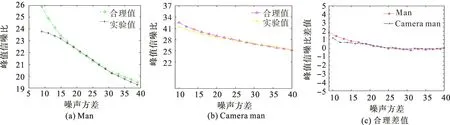
图3 图像Man和Camera man的峰值信噪比及其合理差值Fig.3 PSNR and their resonable difference of image Man and Camera man

从主观上可以看出，经本文算法选取参数后进行的去噪效果较好；对不同方差、不同噪声、不同图像都比较适用，避免了在图像去噪时参数选取盲目性的问题。为从客观上进行分析，算出每张实验图像的峰值信噪比，将这个指标和合理值进行对比，结果如表4。

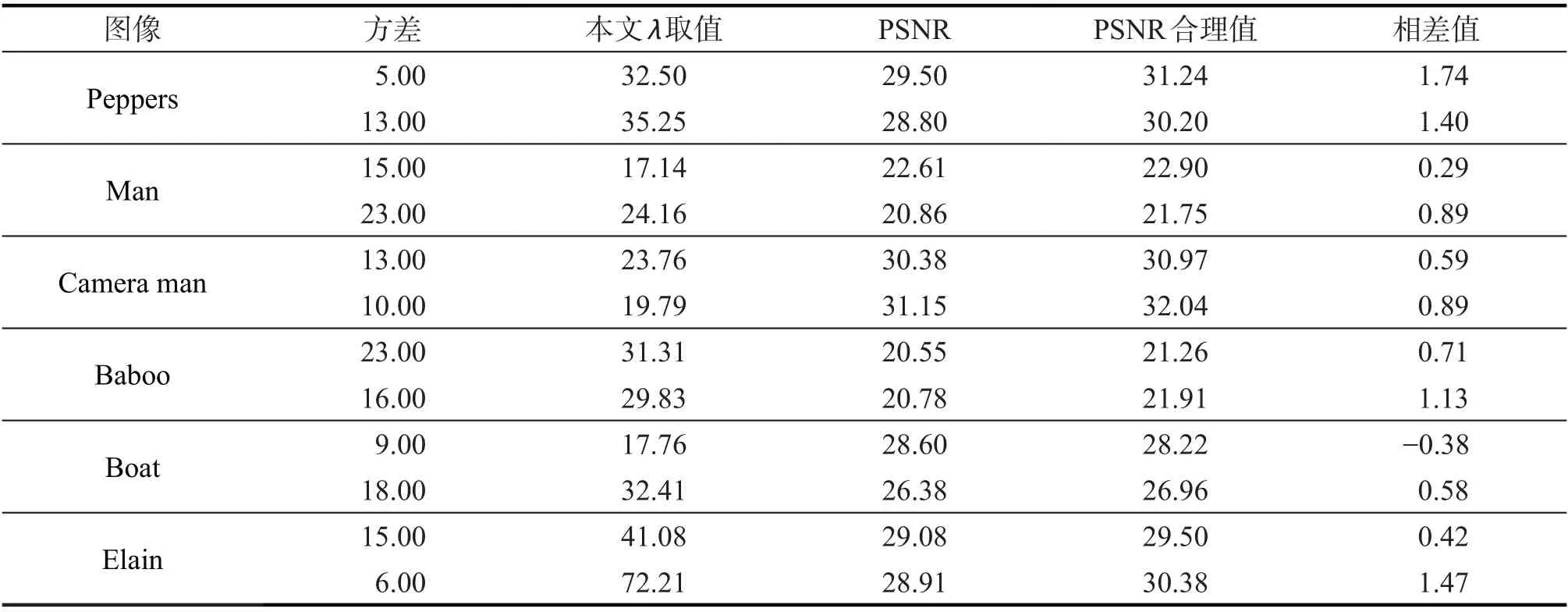
表4 各图像PSNR与合理值对比Tab.4 Comparison of PSNR with reasonable values for each image

从表4可以看出，经自适应选取参数得到的PSNR与合理值非常接近，这就避免了对偶算法中权重主观选取的弊端，有效避免了权重选取过大或者过小的问题，节省了大量测试时间，同时该算法在去噪效果上也是比较好的，具有一定的实际应用价值。

4 结 论

针对全变差去噪模型，首先分析ROF模型的去噪机理，阐述Chambolle对偶原理，利用该算模型求解全变分去噪模型时速度更快，收敛性较好。针对该模型中逼近项和正则项之间的参数选择问题，提出了一种基于能量泛函最小的自适应调整参数方法，弥补了一些传统数值算法中不能对权重进行调整的缺陷。同时通过对不同图像添加不同方差的高斯白噪声和泊松噪声进行仿真实验，从结构相似性、峰值信噪比等方面与合理值进行对比。结果表明，该算法的各项去噪量化指标均可达到较好水平，从而解决了Chambolle对偶算法中参数的主观选取的弊端，提高了图像去噪的效率，具有较好的实际价值。