具有卷积的弱自反环
2020-01-15高蓓蕾王改霞
高蓓蕾,何 萍,王改霞
(安徽工业大学数理科学与工程学院,安徽马鞍山243032)
环的自反性是由群的正交子群推广来的,Thierrin[1]将环中具有“ xy ∈H ⇒yx ∈H ”性质的子集定义为正交。Mason[2]定义了环的自反性概念,将具有自反性的环称为自反环。若对任意a,b ∈R,由ab=0 可推出ba=0,则被称为完全自反环(可逆环)。Kwak等[3]论述了自反环的一些定理和结论,定义了幂等自反环并研究了其性质。Zhao等[4]将自反环作进一步的推广,给出α-自反环的定义及相关结论。Kwak等[5]将满足性质aRb=0 ⇒bRα(a)=0 的环称为右α-斜自反环,类似地也定义左α-斜自反环,并将同时满足左、右α-斜自反的环称为α-斜自反环。Chakraborty[6]给出了中心自反环的定义及相关结论。由此表明,自反环已被大量学者关注和研究。本文在已有研究基础上研究具有卷积的自反环,推广经典环扩张的结论。
1 预备知识

若对任意的a,b ∈R,由aRb=0 可推出bRa=0,称R 为自反环[8]。显然,每个可逆环都是自反环。弱自反环是自反环的推广,称环R 是弱自反环,如果对所有的a,b ∈R,由aRb=0 可推出bRa ⊆N(R)[8]。更一般地,环R 被称为*-自反的,如果对任意a,b ∈R,由aRb=0,可推出aRb*=0。受上述研究启发,定义并引入具有卷积的弱自反环即弱*-自反环,研究具有卷积的弱自反环的性质。显然,弱*-自反环是*-自反环和弱自反环的推广。本文证明每一个弱*-可逆环是弱*-自反环。
2 弱*-自反环的性质
定义1若对于任意a,b ∈R,由aRb=0 可推出bRa*⊆N(R),则称环R 为弱*-自反环。显然,每一个*-自反环都是弱*-自反环,且条件bRa*⊆N(R)和aRb*⊆N(R)是等价的。
命题1若R 是约化的弱*-自反环,则R 是*-自反环。
命题2设R 和S 是两个环,且τ:R →S 是个同构,那么
1) *是R 的一个卷积当且仅当τ(*):=τ°*°τ-1是S 的一个卷积;
2) R是*-自反的当且仅当S 是τ(*)-自反的;
3) R是弱*-自反的当且仅当S 是弱τ(*)-自反的。
证明1)显然,τ(*):=τ°*°τ-1是S 的一个2阶反自同构,且τ-1°τ(*)°τ=*是R 的一个2阶反自同构。易知,若*是R 的一个卷积,则τ(*)是S 的一个卷积。类似地,若τ(*)是S 的一个卷积,则*是R 的一个卷积。2)若R 是*-自反的,则对于任意的a,b ∈S,满足aSb=0,那么

因此

从而

由此,S 是τ(*)-自反的。反之亦然。
3)的证明与2)的证明类似。
命题3设R 是环,则以下条件等价:
1) R 是弱*-自反的;
2)对于R 的任意两个非空集合A,B,若ARB=0,则BRA*⊆N(R);
3)对于R 的所有右(左)理想I,J,若IJ=0,则IJ*⊆N(R);
4)对于R 的所有理想I,J,若IJ=0,则JI*⊆N(R)。

2)⇒3)任取R 的两个右理想I,J,令IJ=0,有IR=I,IRJ=0,由2)可知,JI*=JRI*⊆N(R)。对R 的左理想,可类似证明。
3)⇒4)证明是直接的。
4)⇒1)对任意的a,b ∈R,令aRb=0,那么RaRRbR=0,由4)知

因此,R 是弱*-自反的。
命题4每个*-可逆环是弱*-自反的。
证明如果R 是*-可逆环,那么R 是对称环[6]。对任意a,b ∈R,令aRb=0,可推出ab=0,因此ba*=0。又每个对称环都是半交换的,因此bRa*=0。
定义2若对任意的a,b ∈R,由ab=0 可得ba*∈N(R),环R 为右弱*-可逆的。左弱*-可逆环可类似定义。如果R 既是右弱*-可逆环又是左弱*-可逆环,那么R 被称为弱*-可逆环。
命题5设R 是环,则以下结论成立:
1)如果R 是弱*-可逆环,那么它是弱*-自反的;
2)如果环R 是弱*-自反和半交换的,那么它是弱*-可逆的。
证明1)设R 是弱*-可逆环,若对任意a,b ∈R,有aRb=0,那么ab=0,且对任意r ∈R,有abr=0。由弱*-可逆环的定义可知bra*⊆N(R),即bRa*⊆N(R)。因此R 是弱*-自反的。
2) 设R 是弱*-自反和半交换的环,若对任意a,b ∈R,有ab=0,由R 是半交换环,可得aRb=0,那么bRa*⊆N(R),又1 ∈R,所以ab*∈N(R)。
3 弱*-自反环的一些扩张
命题6对于*-环R,如果卷积*是半刚性的,那么R 是弱*-自反的。
证明若环R 的卷积*满足题设条件,那么对任意a,b,r ∈R,若aRb=0,则有0=(ar*b*Rb)ra*=(bra*)*Rbra*。又卷积*是半刚性的,因此bra*=0,故bRa*=0 且bRa*⊆N(R)。
定义3对任意的a ∈R,如果a=a*,那么称a 是自共轭的。特别地,对于*-环R 的幂等元e,如果e*=e=e2,那么称e 是R 的一个投射。
命题7对于*-环R,以下条件等价:
1) R 是弱*-自反的;
2)对任意的e ∈R,eRe 是弱*-自反的;
3)对任意的中心幂等元e ∈R,eR 是弱*-自反的。
证明2)⇒1)是显然的。
若1)⇒2)R 是弱*-自反环,e2=e=e*∈R,那么对任意的eae,ebe ∈eRe,满足
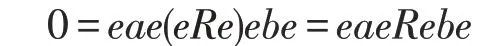
有
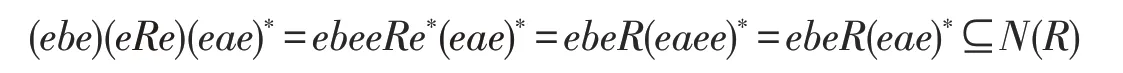
因此,

即eRe 是弱*-自反的。
1)⇒3)由于每个中心幂等元都是投射,证明是显然的。
设R 是环且RMR是双模,则环R 关于M 的平凡扩张T(R,M)=R⊕M 是一个环,其加法运算是矩阵的普通加法,乘法运算定义如下:

说明:如果R 是*-环,T(R,R)是R 关于R 的平凡扩张,那么-*:T(R,R)→T(R,R),即是T(R,R)上的一个卷积。
引理1[9]如果对任意a,b ∈R,aRbRb=0(或aRaRb=0)当且仅当aRb=0,称R 是半素环。
命题81) 如果平凡扩张T(R,R)是弱*-自反的,那么R 是弱*-自反的。
2)如果*是环R 的半刚性卷积,那么T(R,R)是弱-*-自反的。
证明1)若平凡扩张T(R,R)是弱-*-自反的,那么对任意的a,b ∈R 且满足aRb=0,有
又T(R,R)是弱-*-自反的,


因此bRa*⊆N(R),即R 是弱*-自反的。
2)如果环R 的卷积*是半刚性的,那么R 是半素环和弱*-自反环。令

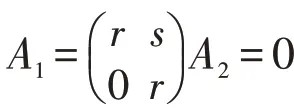

故有a1Ra2=0,

式(1)两边右乘sa2,可得

根据引理1,有

得
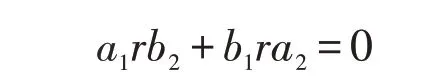
那么a1Rb2=0。又R 是弱*-自反的,有

推论1若R 是约化的弱*-自反环,那么T(R,R)是弱-*-自反环。
命题9若{Ri∶i ∈I}是一类弱*-自反环,那么⊕i∈IRi是弱*-自反环。

如果对任意r ∈R,ur=0,有r=0,环R 的一个元素u 被称为右正则的。左正则可类似定义。一个既是左正则又是右正则的元素叫做正则元。对于一个*-环R,若Δ 是由R 的中心正则元组成的乘法幺半群,那么Δ-1R={u-1a|u ∈Δ,a ∈R}是个环。若I=I*,那么-*:Δ-1R →Δ-1R(满足(u-1a)*=(u*)-1a*)是Δ-1R 的一个卷积。
命题10对于一个*-环R,R 是弱*-自反的当且仅当Δ-1R 是弱-*-自反的。证明若R 是弱*-自反环,对任意的u,v ∈Δ,a,b ∈R,u-1a,v-1b ∈Δ-1R,有

那么aRb=0,根据条件又有bRa*⊆N(R)。则

因此Δ-1R 是弱-*-自反的。
反之,若Δ-1R 是弱-*-自反的,且对任意的a,b ∈R 有aRb=0,那么a(Δ-1R)b=0。又Δ-1R 是弱-*-自反的,

所以有bRa*⊆N(R),即R 是弱*-自反的。
若R 是交换环S 上的一个代数,R 关于S 的Dorroh扩张是R 的扩环D=(R,S),其中ri∈R 和si∈R,D 上的乘法运算为:(r1,s1)(r2,s2)=(r1r2+s1r2+s2r1,s1s2)。如果R 关于卷积*是一个代数,那么有卷积-*:D →D(满足(r+s)-*=(r*,s))。
命题11若R 是交换环S 上的一个代数,那么R 是弱*-自反的当且仅当R 关于S 的Dorroh扩张是弱*-自反的。
证明由于每个s ∈S 可以写作s=s·1R,R={r+s ∶(r,s)∈D}。若R 是弱*-自反的,
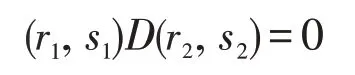
则对任意的(r,s)∈D,

有

因此
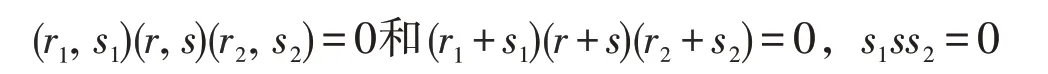
等价,得

若R 是弱*-自反的且S 是交换环,则

得

因此,(r2,s2)D(r1,s1)-*⊆N(D), 即D 是弱*-自反的。
反之,若D 是弱*-自反的,对任意的a,b ∈R,使得aRb=0,那么
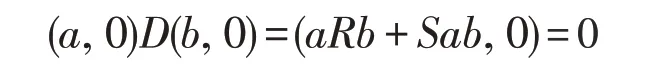
由条件可得,

那么
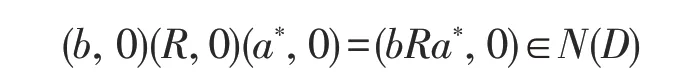
因此,bRa*⊆N(R),即R 是弱*-自反的。
命题12若R 是弱*-自反的拟Armendariz环,则R[x]是弱-*-自反的。

对于一个*-环R,如果理想满足I=I*,那么I 是一个*-环(可能没有单位元)。显然,-*:R/I →R/I(满足(a+I)-*=a*+I)是R/I 的一个卷积。
命题13R 是*-环,理想满足I=I*。如果R/I 是-*-自反的且*是I 的半刚性卷积,则称R 为弱*-自反环。
证明对任意a,b ∈R,aRb=0,由R/I 是-*-自反得bRa*⊆I。且对任意的r ∈R,aRb=0 得

当bra*∈I 且*是I 的半刚性卷积,可得

