千斤顶驱动开合屋盖中伸缩套筒液压缸刚度分析

(1.上海交通大学土木工程系， 上海 200240； 2.上海核工程研究设计院， 上海 200233 )

引言

千斤顶驱动开合屋盖是一种较为新颖的建筑形式，它打破了室内外空间的界限[1]，可运用于体育馆顶盖、核岛安全壳顶盖等结构物。其中液压缸刚度对整体结构受力分析，特别是闭合状态下抵抗台风受力分析有重要的影响。目前针对伸缩套筒液压缸刚度计算研究较少，对单级液压缸刚度研究目前主要有以下方法：不考虑钢材刚度，仅仅考虑液压油作用计算刚度[2]； 将液压缸流体和刚体等各个部分的刚度分别算出,然后按照串联弹簧计算[3]；考虑液压缸缸体在其内部油压变化会产生弹性变形，计算出考虑液压缸缸体变形情况下液压介质的等效弹性模量，然后代入到不考虑缸体变形的刚度计算公式，得到考虑刚体变形的计算公式[4]；在有限元软件中建模，考虑流体压缩性的刚度计算方法[5]。

针对目前研究较少的伸缩套筒液压缸刚度进行分析，提出了多级液压缸刚度计算的理论公式。同时通过三维建模软件建立了液压缸模型，并导入有限元软件ABAQUS，利用软件中包含的“流体腔”和“流体交换”功能，考虑了液体在不同腔体内通过局部油孔相通的影响，也考虑了液压油和钢材流固耦合对刚度分析的影响，提出了伸缩套筒缸刚度的有限元计算模型，为同类建筑的液压缸刚度计算和受力分析提供参考。

1 伸缩套筒液压缸刚度理论分析

根据入油口和出油口分布位置不同，伸缩套筒液压缸分为多种。图1为一种典型的双作用二级伸缩套筒缸的计算简图。级数更多和不同油口布置的液压缸可以用相似方法研究。计算简图中，因刚度分析与液压缸内部油路和微小结构关联很小，所以在建立简化模型时倒角、连通孔、局部油孔、焊缝密封圈等部分被忽略[6]。活塞杆内部中空，与一级缸筒和二级缸筒底部共同形成一个封闭的腔室为正腔。活塞杆壁与一级缸筒筒壁之间形成一级反腔，一级套筒筒壁与二级缸筒筒壁之间形成二级反腔，反腔之间有局部油孔连通[7]，所以实际上只有两个独立的封闭腔体。图1中A1～A7均为绕中心轴对称的圆形或圆环面积。

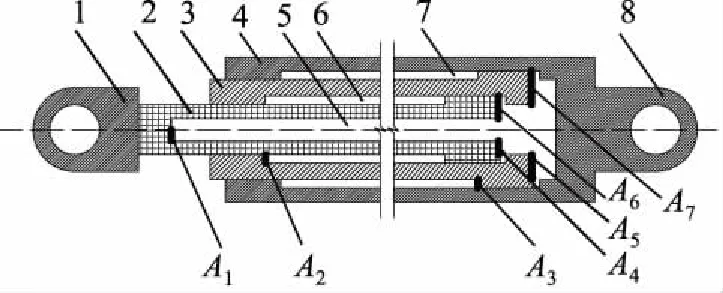
1、8.端环 2.活塞杆 3.一级缸筒 4.二级缸筒 5.正腔 6.一级反腔 7.二级反腔图1 双作用二级液压缸结构示意图

开合屋盖结构中在闭合状态下是否能抵抗台风暴雨为结构设计的关键因素，此时伸缩套筒液压缸处于行程最短状态，其进出油口被液控单向阀锁死，液压缸两腔的油液被严密封闭。图2为建筑结构设计软件设计的开合屋盖结构，在千斤顶驱动下分别为开启状态和闭合状态。

图2 千斤顶驱动开合屋盖结构

根据漏油状况和锁住进出油口的时机以及背压系统的作用等因素[8-9]，液压缸在无外力作用下可能因为正腔和反腔压强的相对大小而出现以下四种初始状态，如图3所示。

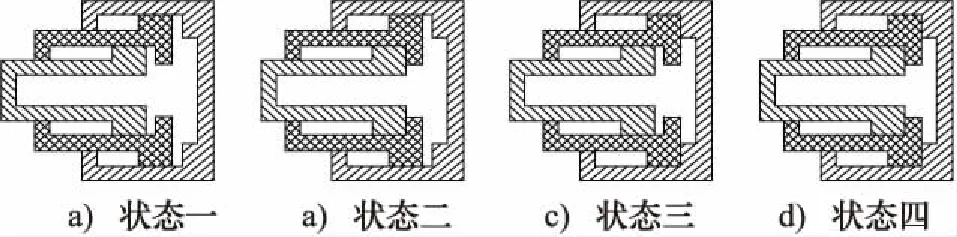
图3 液压缸状态示意图

根据二力平衡原理，在无外力作用下，活塞杆与一级缸筒底部不分离时，压强应当满足关系式：

p1(A1+A6)-p2A2<0

(1)

其中，p1和p2为图1中正腔、反腔相对外界的初始压强，Pa；A1～A7为图1中表示的面积，m2。满足式(1)条件下时，若一级缸筒和二级缸筒底部不分离，即处于状态四时，p1和p2应满足关系式：

p1A7-p2A3+p1(A1+A4)<0

(2)

不满足式(1)条件下时，若一级缸筒和二级缸筒不分离，即处于状态三时，p1和p2应满足：

p1A7-p2A3+p2A2-p1(A6-A4)<0

(3)

当式(1)和式(2)中不等号改为等号时会出现状态一，当满足式(1)同时式(2)改为等号时会出现状态二。其中正腔、反腔中的液压油均满足下式[10-11]：

(4)

其中，G为体积模量，Pa;p为液压油压强，Pa;V为正反两腔液压油体积，m3;V1,V2分别为正腔、反腔的初始容积，m3。对于状态一、二级缸筒连接的端环中心固定，当有外力作用在活塞杆连接的端环上时:

ΔF=Δp2A2-Δp1(A1+A6)

(5)

ΔV1=ΔL1(A1+A6)-ΔL2(A7-A6+A4)

(6)

ΔV2=-ΔL1A2-ΔL2(A3-A2)

(7)

其中，ΔF为沿着液压缸中心轴线的外力变化量，kN；ΔV1，ΔV2为外力作用下，正反两腔相对初始平衡状态下的体积变化量，m3； ΔL1，ΔL2分别为活塞杆和一级缸筒相对二级缸筒相对初始平衡状态的位移变化，m。

将式(4)～式(7)带入刚度定义公式：

(8)

同理可以推导状态二、三的刚度公式分别为：

(9)

(10)

其中，K1，K2，K3为状态一到三液压缸的刚度，kN/m。

以上状态一到三的刚度公式均只考虑了液压油对液压缸刚度的影响。这是因为液压油的体积弹性模量为(1.4～2)×109Pa,其可压缩性约比钢材大100～150倍[12]。在状态四下液压缸受压时，油体压缩对刚度影响很小，主要是钢材直接接触传力。基于这种传力路径，提出一种简化的计算公式，即把液压缸简化为面积与活塞杆横截面积A相同，长度L为液压缸长度的实心钢杆，E为钢材弹性模量，则刚度简化公式为K4=EA/L。

2 伸缩套筒液压缸刚度有限元分析

液压缸主要由外部的钢材和里边的液压油组成。若更准确分析其刚度时既需要考虑外部钢材即固体的受力，也要考虑内部液压油即流体的受力。流固耦合力学的重要特征是两相介质间的交互作用，即固体在流体载荷作用下会产生变形或运动，而变形或运动反过来又影响流场的流动，从而改变流体载荷的分布和大小，所以基于流固耦合的液压缸受力分析会更加合理。

ABAQUS有限元软件提供一种基于面的流体腔单元，可以利用流体腔单元来提供充液结构的变形和流体在结构腔边界上施加的压力之间的耦合，也可以使用流体交换定义来模拟流体在腔和环境之间或多个腔之间的流动[13]，如图4所示，从而可以对液压缸进行流固耦合受力分析。

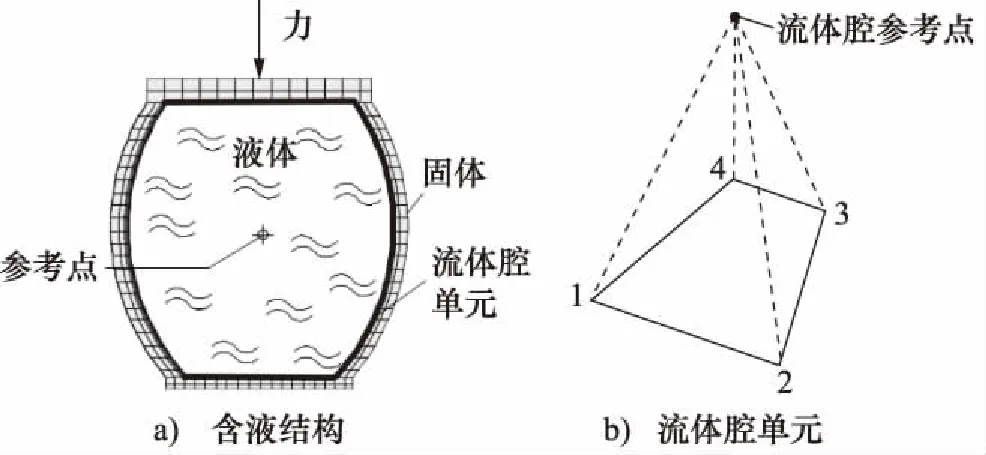
图4 ABAQUS流体腔含液结构

液压缸的零件十分复杂，由上述分析可知其构件多、倒角多、细小孔洞多、连接螺栓多。过碎小的细部构造对液压缸整体刚度分析并无较大影响，但会大大地加大有限元软件的计算量。所以在建立有限元模型时，倒角、连通孔、进出油口等部分被适当简化。通过建模软件CREO分别建立四种状态下的三维模型，通过IGES格式导入有限元软件ABAQUS中，建立液压缸模型，如图5所示。图5a为状态一下剖开一半的三维模型，图5b为状态一下整体的三维模型。

图5 双作用二级液压缸ABAQUS模型

导入ABAQUS后，分别对正腔、一级反腔、二级反腔内部定义基于面的“流体腔”单元，同时对一、二级反腔定义“流体交换”来确保其压强相同，流体相通。两个端环分别与临近的活塞杆及外套筒定义绑定约束。对靠近二级缸筒的端环中心建立参考点，耦合约束端环的内侧面，并固定此参考点。对靠近活塞杆的端环中心和一级缸筒分别建立参考点耦合约束，固定其参考点。活塞杆和一级缸筒之间接触面切线方向采用无摩擦约束，法线方向采用硬接触。一级缸筒和二级缸筒之间接触面切线方向也采用无摩擦约束，法线方法也采用硬接触。同时，在ABAQUS中输入物理参数，其中液压油的体积模量为0.7×109Pa，密度为870 kg/m3，动力黏度为0.039 Pa·s。缸套筒和活塞杆采用45号钢材，其密度为7890 kg/m3，杨氏模量为2.09×1011Pa，泊松比为0.269。在ABAQUS中首先对含液腔体充油，使两个独立的腔体油压分别达到p1和p2，其中p1和p2需要满足上一部分分析得到不等式(1)～式(3)及相应的等式，整个液压缸达到初始平衡状态。然后在第一活塞杆参考点施加压力，同时释放耦合在活塞杆和一级缸筒上参考点中的沿液压缸轴线方向的自由度。最终获得有限元输出活塞杆端环中心的位移，通过计算输入力和位移比值到刚度。

分别采用两种思路运用ABAQUS对液压缸进行分析。第一种思路将钢材设置为刚体。通过不考虑钢材变形求解刚度数值，来验证第一部分提出理论公式。第二种思路将钢材设置为变形体。其结果考虑了钢材和液压油相互力和位移的影响，求解刚度结果接近实际情况。上述ABAQUS的操作就是将钢材当变形体。在运用第一种思路研究时，ABAQUS设置基本与第二种思路设置基本相同，但需要在“约束”模块里增加刚体约束，分别将活塞杆、一级缸筒、二级缸筒设置为刚体。

对于状态一，外部压力设为1 kN，按思路一有限元计算得到的位移为0.004083 m, 刚度为244.917 kN/m。按理论公式(8)计算的结果为245.427 kN/m。有限元计算结果与提出的理论公式误差为2.1‰，证明了理论公式推导的正确性和有限元模型的准确性。将钢材从刚体改为变形体时，即采用思路二分析时，有限元计算得到的位移为0.004975 m，刚度为201.005 kN/m，比理论公式(8)小了18.1%，这是因为变形体考虑了钢材受压时也会缩短，同时也考虑了流固耦合影响下筒壁受压轻微膨胀变形所以减小了整体刚度，所以有限元思路二计算的结果，虽与提出的理论公式有一定偏差，却更接近于实际刚度。

对于状态二、三采用与状态一相同的分析方法，将计算结果写入表1。由表可见, 思路一有限元分析的计算结果和理论式(8)～式(10)偏差均不超过2.1‰, 证明了理论公式推导的正确性和有限元模型的准确性。思路二有限元分析的计算结果得到了更接近真实状况下的刚度值。对于状态四，由于刚度主要是钢材接触传力，液压油压缩传力影响很小，所以只将其作为变形体采用思路二进行分析。

表1 刚度计算结果汇总

图6为四种状态下变形体的位移云图，为采用思路二施加荷载后的最终位移状态。对于状态一，根据ABAQUS中状态一到四后处理位移云图动画，可以看出在外力作用下，不同初始状态下的液压缸转化趋势。有外力作用时，活塞杆与一级缸筒的运动方向相反。由于状态一刚度小，所以在较小的拉力作用下，会从状态一转变为状态三，在较小的压力作用下，会从状态一转变为状态二。对于状态二，由于刚度很大所以不易转换状态，在较大的拉力作用下可转为状态一，在较大的压力作用下变为状态四。状态三也不易转换状态，拉力作用下仍为自身状态，压力作用下转为状态一。状态四在压力作用下仍然维持自身状态，在超过一定拉力作用下变为状态三。

图6 ABAQUS液压缸位移云图

3 结论

(1) 推导了一种二级双作用液压缸在不同初始状态下的刚度计算公式，更多级数或者不同进出油口布置位置的液压缸刚度公式也可以用相似的方法推导得出；

(2) 建立了二级液压缸在不同初始状态下的三维模型，提出了基于有限元软件ABAQUS并考虑钢材和液压油流固耦合作用的刚度计算方法。并根据钢材是否为变形体提出了两种有限元分析思路。分别用两种思路计算了四种初始状态的二级液压缸刚度。通过理论公式和有限元第一种思路计算结果对比，验证了有限元模型和理论公式的正确性。并通过第二种思路计算结果得到了更接近真实状态下的液压缸刚度，为同类千斤顶驱动开合屋盖工程计算液压缸的刚度提供了一种方法；

(3) 分析了不同初始状态下伸缩套筒缸分别在拉压力下状态的转化趋势。不同初始状态下刚度差别很大。状态一在初始状态下的液压缸刚度很小所以在外力作用下容易转化为其他状态，而状态二、三、四的刚度相对比较大，不容易转化为其他状态。