电液伺服阀用微位移放大机构发展现状

刘国平， 何忠波， 郑佳伟2， 周景涛， 柏 果

(1.陆军工程大学石家庄校区， 河北石家庄 050003; 2. 32184部队， 北京 100072)

引言

随着航空航天、国防工业的快速发展，电液伺服系统的应用越发广泛。电液伺服阀(Electro-hydraulic Servo Valve,EHSV)作为电液伺服系统的核心部件，对系统的静、动态特性起着关键作用。传统电液伺服阀结构形式较为复杂，响应速度较慢，且系统阶次较高，对控制器设计要求较高。直驱式伺服阀具有响应频率高、输出位移大、抗油污性能好的特点，可实现恶劣条件下的稳定输出，具有较为广泛的应用前景。但基于压电陶瓷(Piezoelectric Ceramics,PZT)、超磁致伸缩材料(Giant Magnetostrictive Material,GMM)等新型材料的阀用致动器输出位移仅为微米级，难以满足直驱式伺服阀要求，因此需要设计相应的微位移放大机构[1]。

本研究针对现有的伺服阀用微位移放大机构进行了分类梳理，比较了不同类型放大机构的优势和不足，阐述了各自的适用范围，在此基础上，分析了放大机构的发展趋势。

目前应用于微致动器的换能材料主要有压电陶瓷、超磁致伸缩材料、形状记忆合金(Shape Memory Alloy,SMA)等，这些材料拥有优良的力学性能，具有较大的输出力或延伸率，在精密驱动领域具有较好的发展前景[2-3]。但基于这些材料的微位移致动器输出位移一般很小，难以满足大行程机构的驱动需求。

日本学者TAKAHIRO URAI等[4-6]设计的GMM直驱式伺服阀，采用GMM棒直接驱动阀芯，其阀芯位移仅为50 μm，流量仅为2 L/min；李立毅[7]设计的管状GMM直驱式伺服阀在100 Hz驱动频率下，其流量仅为1.999 mg/s。

微位移放大机构可很好地解决致动器输出位移不足的问题，一般通过机械放大或液压放大的方式，放大比可达2.34～15.6，基本满足了输出位移需求。

目前，微位移放大机构形式多样，应用于精密机械领域的微位移放大机构主要分为机械式和液压式两种。

机械式放大机构通常采用柔性铰链结构，其优点在于运动过程无空回行程、无摩擦、运动平滑、分辨率较高[8]；同时也普遍存在承受载荷小、抗冲击能力较差、体积较大等问题。对于机械式放大机构，国内外研究成果较为丰富，提出了基于柔度理论、弹性梁理论、卡式定理等原理的研究思路，为机械式放大机构的设计和研究提供了较为完备的理论体系。

液压式微位移放大机构基于帕斯卡原理，利用大活塞的位移推动密闭容腔内油液运动，并最终带动小活塞产生较大的位移。相比于机械式微位移放大机构，液压式微位移放大机构占用空间较小，位移放大比较大，频带更宽[9]。但液压式放大机构存在泄漏问题，另外其复杂的工艺特性也导致加工困难，装配精度难以满足设计需求等问题。国内外学者主要致力于解决活塞运动造成的磨损和泄漏问题，提出了不同的解决方案。

1 机械式微位移放大机构

机械式微位移放大机构一般采用柔性铰链结构，利用柔性铰链的弯曲变形使机构在某一方向上得到放大的平动位移。柔性铰链结构，避免了由于运动副相对运动带来的摩擦损耗，因此在微位移放大机构中得到了较为广泛应用。

1965年J.M.PAROS和L.WEISBORD[10-11]设计了矩形截面、圆柱切割形式的柔性铰链，推导出了柔性铰链的设计公式，并给出柔性铰链远小于其切割半径条件下的简化公式，给柔性铰链的设计计算带来了极大的方便。吴鹰飞[12]利用力学的基本公式对柔性铰链的设计公式进行推导，得到了相对于J.M.PAROS公式更为简洁的一般公式，在柔性铰链厚度接近其切割半径的条件下，其公式更加精确和简洁。

J.M.PAROS设计的柔性铰链结构较为简单。随着柔性铰链结构在微位移放大机构中的广泛应用，其结构形式得到了很大丰富。

于志远[13]定义了新参数λ——柔性铰链凹口处长与宽的比值，进行了有限元仿真，讨论了直梁型、圆角直梁型、椭圆型、抛物线型和双曲线型柔性铰链输出位移与λ的关系。

LING Mingxiang等[14]将矩阵位移法与传递矩阵法相结合，提出了一种基于柔性铰链的混合串并联柔性机构的动力学静态建模方法，给出了精确、简洁的求解方法，具有较好的预测精度，为设计初期快速进行性能评价和参数优化提供了依据。

崔新辉[15]对柔性铰链结构进行了梳理，从结构形状的角度对柔性铰链结构作了分类，如图1所示。

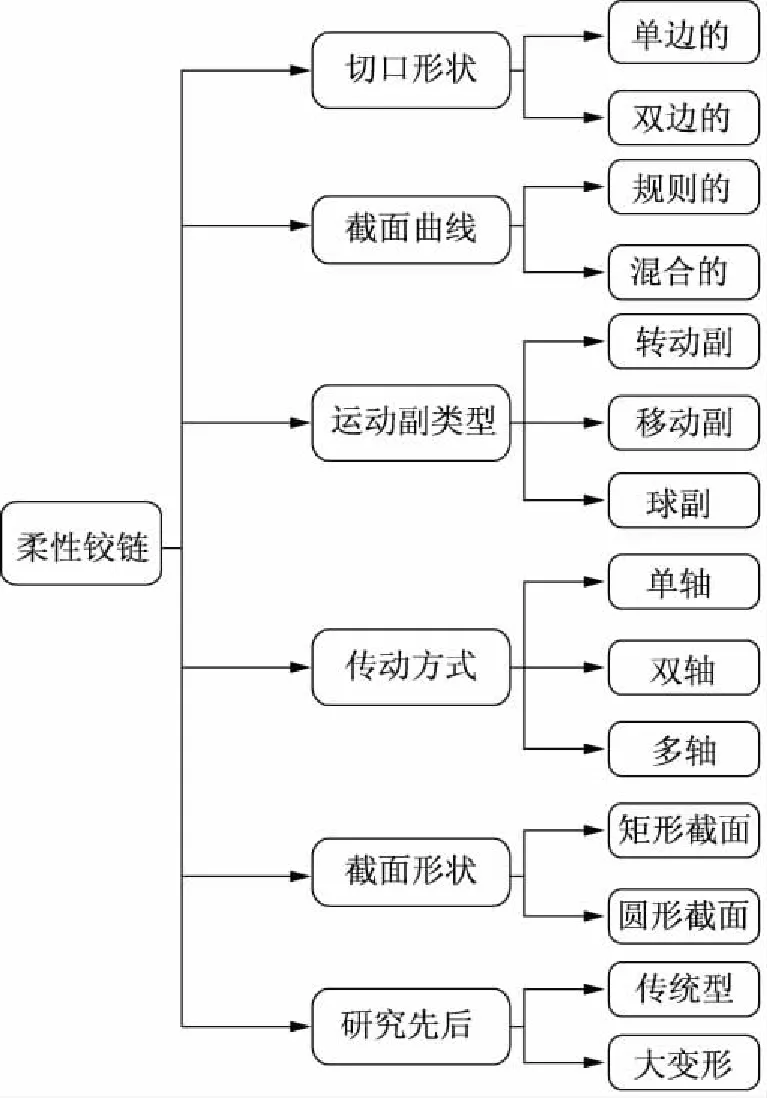
图1 柔性铰链分类

根据目前柔性铰链放大机构的作用原理和结构形式，大致可以将柔性铰链放大机构分为杠杆式、三角式和弓张式3种，不同学者对其分别进行了研究，并根据不同的应用环境，设计了形式多样的放大机构。

1.1 杠杆式放大机构

杠杆式放大机构结构较为简单、加工难度较低，具有较高的线性度和能量利用率，其结构一般如图2所示。

图2 杠杆式放大机构

杠杆放大机构中，杠杆部分可以视为刚体，其受力可以简化成如图3所示。

图3 杠杆式放大机构受力原理

单级杠杆式放大机构，放大比很小，应用范围有限。因而一般采用多级结构，以增加放大比，满足输出位移的需求。

沈剑英等[16]开发了一种二级杠杆微位移放大机构，并在考虑柔性铰链转动中心偏移量的基础上，推导出杠杆式柔性铰链二级放大机构的放大率计算方法，其结构原理如图4所示。

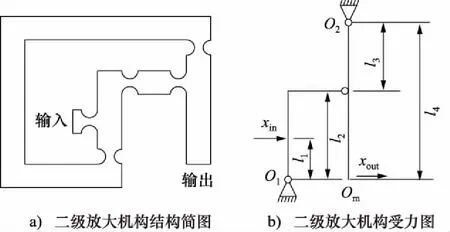
图4 二级杠杆放大机构及受力

其得到的放大率计算公式为：

(1)

其中,xout为输出位移；xin为输入位移；p1,p2,p3,p4,p5,p6为尺寸参数，与l1,l2,l3,l4,l5,l6有关；kF为柔性铰链的轴向拉压刚度；kM为柔性铰链的转角刚度。理论计算的放大率为8.31，有限元仿真分析的放大率为8.38，实验测试得到的放大率为8.20，三者的结果非常接近。

黄志威[17]采用半圆型柔性铰链设计了一种反对称式柔性放大机构，如图5所示。通过反对称设计，可将输入的直线位移放大并转化为转角位移输出。直线位移转化为角位移的转化率η=1.2×10-4rad/μm。

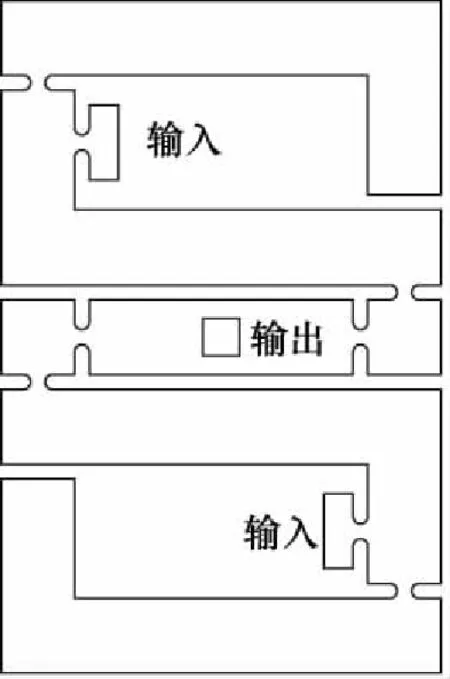
图5 杠杆式位移-转角放大机构

多级杠杆式放大机构，设计原理比较简单，放大率可达到较高水平，但空间尺寸太大，不利于工程化应用和小型化发展。

1.2 三角式放大机构

三角式放大机构采用三角形放大原理，如图6所示。

图6 三角放大原理

直角三角形三边长分别为a、b、c，固定一条直角边a，当斜边c伸长Δc时，另一条直角边b伸长Δb。

根据勾股定理，有：

a2+b2=c2

a2+(b+Δb)2=(c+Δc)2

(2)

忽略二阶无穷小量Δb2和Δc2，则放大率：

(3)

SUJIT PARDESHI等[18]设计制造了基于三角原理的微位移放大机构，如图7所示，建立了伪刚体模型，进行了有限元方法仿真和实验，实际放大倍数约为1.5倍。

图7 三角放大机构

姚俊飞[19]开发了一种基于三角形原理的三角位移放大机构，其结构如图8所示，利用2个致动器作为输入，由于输入端驱动机构与放大机构之间依然存在磨损，实际放大倍数约为3.2倍。

图8 双致动器三角放大机构

黄卫清[20]基于三角原理，设计了一种双向主动输出的菱形微位移放大机构，如图9所示，通过对称结构设计，利用4个致动器，可实现双向主动输出。经理论计算和实验，放大倍数约为2.5倍。

图9 主动式三角放大机构

三角式放大机构原理简单，但依然存在空间利用率低、尺寸过大的问题，同时放大比也不够理想。

1.3 弓张式放大机构

弓张式放大机构在柔性铰链放大机构中应用较广，效果较好，目前研究也更为充分。MA[21]采用运动学理论分析了弓张式柔性铰链的理想位移放大比，并将柔性铰链视为具有理想枢轴的纯多刚体。在考虑平移和旋转刚度的条件下，采用弹性梁理论分析了理论位移放大率。其理论位移放大率的模型解释了弓张式位移放大机构具有放大率极值和阈值的原因。

LOBONTIU等[22]利用卡氏第二定理推导了弓张式柔性放大机构刚度的闭环解析公式，并研究了相关几何参数对刚度的影响趋势。RYU[23]采用矩阵分析的方法对弓张式柔性放大机构的变形进行分析，理论分析结果与实验测试结果的误差小于10%；KIM等[24]利用同样的方法对空间弓张式柔性放大机构(2个二维弓张式柔性机构交叉联接)的变形进行分析，通过实验测试其分析误差也小于10%。

张兆成[25]设计了弓张式放大机构，建立了该柔性机构的简化模型，如图10所示。利用卡氏第二定理推导了其刚度方程，将柔性机构简化为单自由度弹簧质点系统，得到了其固有频率。但其将柔性机构离散化为单自由度质量——弹簧系统，将柔性铰链之间的连接杆视为绝对刚体，又难以精确推导等效质量，所得固有频率误差较大，为14.1%。

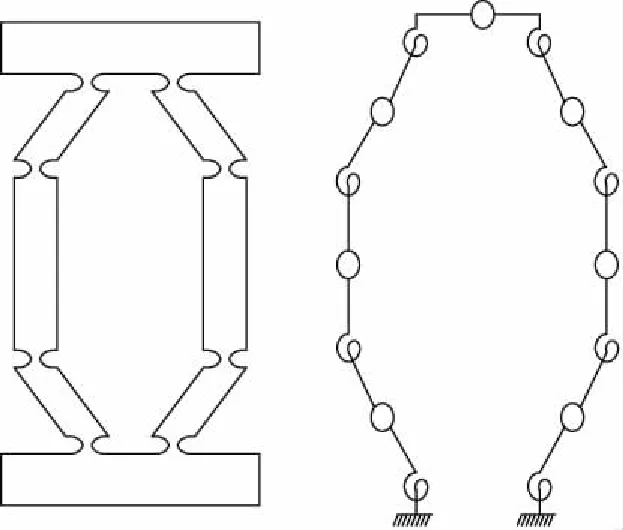
图10 弓张式放大机构及简化模型

万嘉辉[26]利用功能原理，将放大机构整体移动副刚度与柔性铰链转动刚度统一考虑，推导了整体机构位移输出及放大比的影响参数。

叶果等[27-28]利用弓张式放大机构对称性的特点，建立了1/4数学模型，采用矩阵法建立了其柔度矩阵，推导了弓张式放大机构的输出位移公式及位移放大公式，并进行了仿真和实验验证。基于模态分析理论，根据拉格朗日方程建立了弓张式放大机构的运动微分方程，给出了计算弓张式微位移放大机构固有频率的解析式。

郑佳伟[1]设计了一种双排串联式弓张结构，如图11所示，分析了其结构尺寸参数对其放大比的影响，并制作了样机，对其性能进行了测试，所得放大率约为16.5。

图11 双排串联弓张式放大机构

MIKIO MURAOKA等[29]采用蜂窝状设计，提出了一种阵列型机械放大器，如图12所示，结构更加紧凑，有效提高了放大机构的空间利用率。

图12 列阵弓张式放大机构

WEI DONG等[30]采用混合柔性铰链，设计了具有多级放大的弓张式放大机构，如图13所示，基于柔度矩阵法和拉格朗日法进行了动、静力学分析，并制造了放大倍数为48的样机。

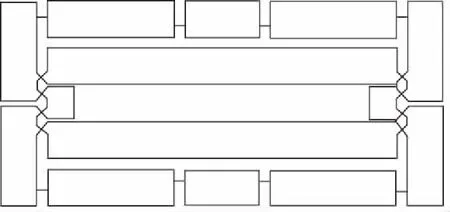
图13 多级弓张式放大机构

LING MINGXIANG等[32]设计了一种具有大范围和高频率的两级弓张式放大机构，如图14所示，采用弹性梁理论，进行了动、静态分析，通过定义阻抗因子，建立了位移放大比公式，描述了第二层对前一层的阻碍作用[31]，进行了有限元仿真，制造了样机最大行程范围为1.44 mm(±720 μm)，基频为628 Hz。

弓张式放大机构兼顾了空间利用率和放大比，实际效果相比于其他机械结构较为理想，但由于机械式放大机构主要依靠柔性铰链以避免运动副间能量损失，而柔性机构本身的变形依然消耗的应变能，以及机构内部存在内反力，造成实际放大倍数的降低，并与理论计算间的误差通常在10%以上，放大效果依然不够理想。同时机械式放大机构一般尺寸较大，空间利用率不高，距满足工程化和小型化应用的要求还存在一定差距。

图14 两级弓张式放大机构

2 液压式微位移放大机构

液压式放大机构不存在内反力，可进一步减少能量损失。同时由于液压式放大机构一般体积较小，空间利用率也有很大提高。液压式放大机构一般利用帕斯卡原理，通过大活塞的微位移推动密闭容腔内油液运动，并最终带动小活塞产生较大的位移，主要有活塞式和膜片式两种。

2.1 活塞式液压放大机构

HWAN-SIK YOON[33]设计了一种具有圆柱形流体室的液压放大机构，如图15所示，其一侧具有小开口而另一侧具有大开口。当较大开口中的活塞被致动器推动时，流体被加压并且将小开口中的活塞推动更长的距离。行程由2个开口的面积比决定。

图15 活塞式液压放大机构

李昕等[34]基于活塞式液压放大机构，建模分析了液压放大机构的动态特性，与输入致动器进行了耦合，得到了放大机构的输入输出函数，并讨论了弹簧刚度对系统响应频率和机构刚度的影响。

2.2 膜片式液压放大机构

俞军涛[35]设计了一种新型的液压微位移放大结构，由柔性铰链膜片式大活塞、密闭容腔、小活塞及压力调节和测量装置构成，对膜片结构的刚度进行了理论分析和数值计算验证。仿真结果表明，该液压放大机构的位移放大倍数为9，阀芯位置控制误差小于1%。

杨朝舒[36]改进了液压式微位移放大机构，如图16所示，该机构将原有刚性活塞改为柔性活塞，直角连接改为了梯度连接，避免了摩擦、爬行，减少流阻、缩流和困油现象。

图16 柔性膜片式液压放大机构

吴家龙等[37]设计了一种波纹管式多膜片全封闭液压放大机构，如图17所示，采用碟形膜片焊接成型的办法，较好地解决液压放大机构的泄漏问题，考虑了腔内油压对放大系数的影响，放大倍数为3.522。

图17 波纹管式多膜片液压放大机构

液压式放大机构的发展受到工艺特性的限制，国内学者关注度不够，目前满足输出需求的成熟设计较少。

3 结论

本研究介绍了伺服阀用微位移放大机构的工作原理，梳理了其发展脉络，比较了不同形式的放大机构的优缺点，总的来看，放大机构理论经历了由简到繁，由粗到细，结构形式由大到小，放大比由小到大的发展阶段。

(1) 阀用微位移放大机构的理论研究由最初的单纯研究应力-应变关系，发展为综合利用功能关系、卡式定理、振动理论、矩阵理论等，理论研究的深度有了进一步提高，建立模型更加精细准确；

(2) 机械式阀用微位移放大机构结构形式更加多样，从杠杆放大到三角放大、弓张放大，机械式放大机构在应用原理和结构形态上都发生了较大变化。不同学者，综合考虑了空间利用率和能量利用率，设计了形态多样的放大机构；

(3) 机械式放大机构相对于致动器空间尺寸太大，空间利用率不高，需要优化结构设计，提高空间利用率。同时，机械式放大机构存在内反力损耗，能量利用率不够高，对放大倍数影响较大。目前通行的做法是采用多个致动器，在增大了放大倍数的同时，增大了控制难度，降低了控制精度；

(4) 液压式微位移放大机构比机械式空间利用率更高，在小型化发展和工程化应用中，具有一定的应用前景。但液压式放大机构存在较为严重的油液泄漏情况。采用膜片焊接成型的方法，虽然解决了泄漏问题，却降低了结构的放大倍数；

(5) 膜片式液压放大机构由于油液压缩和膜片变形，吸收了部分能量，导致输出端输出刚度较低，对机构放大倍数有较为不利的影响。