求解车辆路径问题的量子差分进化算法
2020-01-152
2
(1.浙江工业大学 特种装备制造与先进加工技术教育部重点实验室,浙江 杭州 310014;2.中国计量大学 现代科技学院,浙江 杭州 310018)
量子进化算法最早由Han等[1]在Narayanan等[2]的量子遗传算法概念基础上提出,用于求解组合优化问题。该算法将量子理论与进化计算相融合,用量子位编码表示染色体,通过量子门旋转实现进化操作,具有并行度高、全局搜索能力强和收敛速度快的特点,已被应用于多种类型的车辆路径问题,如王万良等[3]将其应用于求解车辆共享带软时间窗的动态需求VRP问题;李川[4]应用量子进化算法解决了随机车辆路径问题;赵燕伟等[5]应用其求解了多车型同时取送货的低碳路径问题,研究结果表明量子进化算法对VRP,TSP等问题具有良好的求解效果。近年来对车辆路径问题的求解研究趋向于多种方法融合,如陈晓眯[6]将禁忌搜索算法与交叉算子相结合求解动态车辆路径问题;赵燕伟等[7]提出用超启发式算法求解选址-路径问题。与其他算法的融合也正成为量子进化算法研究的一个重要趋势,量子差分算法由Wang等[8]提出将差分进化算法较强的局域搜索能力与量子进化算法的全局搜索能力相结合,实现更高效的搜索效果。张晓雷[9]将该算法应用于函数极值优化,多个案例的应用比较结果显示算法的寻优能力得到明显改进;常新功等[10]提出了分解的多目标量子差分算法,并将其应用于测试函数,验证了算法在非凸函数收敛性及分布性方面的改善;陈晓峰等[11]提出了一种实数编码的量子差分算法,将量子比特概率幅表示为染色体的实数编码,并与差分算法相结合提高算法的性能,在对函数极值及TSP的测试中验证了算法的有效性。
尽管量子差分进化算法在解决众多的NP-hard问题时获得了良好的效果,但这种算法应用于VRP的效果还有待于研究。笔者将量子差分进化算法应用于求解车辆路径问题(CVRP),根据VRP问题特征,基于差分进化策略设计了量子交叉和变异方法以控制种群的进化方向,同时设计动态量子旋转门的量子进化算法进行变领域搜索,通过两种方法的协同进化增强算法的全局搜索能力,典型算例及标准算例的仿真实验结果验证了算法的有效性及鲁棒性。
1 模型构建
1.1 问题描述
CVRP可以描述为由一个配送中心为多个顾客服务,车辆从配送中心出发,配送完成后返回到出发的配送中心,问题的目标是获得总距离最小的最佳配送方案。将顾客与配送中心组成的网络图设为G=(N,A),N=Nm∪Nc,Nm=0为配送中心集合,Nc=(1,2,…,c)为顾客点集合,A={(i,j)∶i,j∈N,i≠j}点i,j的弧集合,K=(1,2,…,k)为车辆集合,dij为i,j的距离,车辆的载重限制为QC,qi为i点需求。为了便于建模,对问题进行如下假设[4]:1) 车辆匀速行驶,路上无拥堵现象,路况平稳;2) 配送车辆数量不限,车辆类型只有一种;3) 客户需求已知并确定,每个客户必须且只能被服务一次。
1.2 模型建立
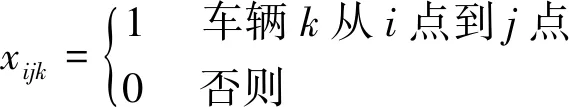
(1)
约束条件为
(2)
(3)
(4)
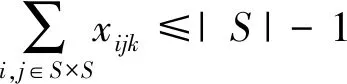
(5)
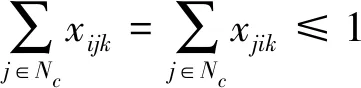
(6)
xijk∈{0,1} ∀i,j∈N,k∈K
(7)
其中:式(1)表示距离最短的目标函数;式(2,3)保证每个顾客只能被服务一次;式(4)为顾客需求限制;式(5)消除顾客点间出现的子回路,式中S为非空顾客点集;式(6)保证每辆车配送完后回配送中心;式(7)表示变量的取值。
2 量子差分进化算法
2.1 量子编码与解码
量子差分进化算法(QDE)采用与量子进化算法相同的染色体表示形式,将量子比特Q-bit(又称量子位)组成的串作为量子染色体,一个量子位|φ>可以处于|1>或者|0>状态,也可以是两种状态的线性叠加,即可以将量子位表示为|φ>=α|0>+β|1>,α,β分别表示0>和1>的概率幅;|α|2表示量子位处于|0>的概率,|β|2表示量子位处于|1>的概率,α2+β2=1,通过量子门的驱动实现最优进化。

将α,β矩阵转换成二进制矩阵G,即
(8)
式中r为均匀分布的随机数0~1。
将G矩阵解码成满足车辆载重要求的顾客集,解码过程为从G中随机选择第一个顾客i,若其满足式(4)的载重要求,则将其放入该车顾客集中,针对所有未放入车中在待配送顾客,确定下一个配送顾客l,即
(9)
若l满足式(4)载重要求,则将其放入该车中,将l移出待配送顾客集,否则计算其他未配送顾客与i的距离,按式(9)依次选择,若没有顾客能放入该车辆,则建立一个新的车辆群重复前面的过程,直到所有顾客都分配车辆,图1为某一解码后的结果,图1表示15 个顾客的配送方案。由图1可知:该方案需要两辆车,第一辆车的配送顺序为“配送中心0-6-2-9-4-11-13-配送中心”,第二辆车为“配送中心-5-1-3-7-8-10-12-14-15-配送中心”。

图1 解码结果示例
Fig.1 Example of a problem decoding
2.2 量子变异

(10)
式中:m1,m2,m3∈{1,2,…,Popsize},m1≠m2≠m3;F为收缩因子,其取值为[0,1]的值;rand为[0,1]间的随机数;g+1为当前代数的下一代。
2.3 量子交叉
量子交叉的发生概率由交叉因子Cr值控制,对选定的父代个体进行交叉混合,以产生新的多样性个体,即
(11)
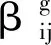
2.4 量子更新
量子门旋转是量子进化算法实现状态转移的主要方法,笔者设计动态量子旋转门进行状态的更新与转移,即
(12)
由式(12)可知,旋转角与当前代数的解及当前最优解有关,且随着迭代次数的增加,旋转角逐步减小,从而有利于在最优解附近进行局部搜索。
其中
(13)
(14)

2.5 量子选择
对由量子交叉、变异及量子旋转更新后的量子比特按照贪婪原则进行选择,具体操作为
(15)
式中f为解码后的适应度函数。由式(15)可知:若通过量子交叉、变异后解码得到的解优于当前解时则将其量子比特由量子交叉、变异更新,否则将量子由量子旋转门更新。
2.6 局部优化
笔者算法的局部优化采用2-Opt和Move方式。
1) 2-Opt:将线路中用(i,j)和(i+1,j+1)代替(i,i+1)和(j,j+1),同时线路方向反转,若交换后,线路距离减少,则交换,图2是其示意图。

图2 2-Opt操作过程示意图Fig.2 Representation of 2-Opt operator
2) Move:依次将同车辆中的顾客移动到该车其他位置,若其距离减少,则执行该操作。
2.7 量子差分进化算法的求解流程
量子差分进化算法流程如下。
Step1初始化令n=1,θ=θ0,α=αt,β=βt,生成初始量子比特种群Q(t)。
Step2按2.1节解码生成初始路线。
Step3按2.6节的局部优化方法调整方案,若调整后解获得改善,则替换原方案,否则不替换;按式(1)计算目标函数值,保留最优个体。
Step4判断是否满足终止条件,若满足,则输出最优解;若不满足,则转Step 5。
Step5按式(14)进行量子选择,得到新的下一代量子比特种群Q(t+1)。
Step6t=t+1,转Step 2继续执行。
3 实验及结果分析
3.1 参数设置
取收缩因子F=0.05,量子交叉Cr=0.5,Δθt=0.05π采用matlab2010b编程,计算机配置为Intel Core i7-3630QM 2.40 GHz,8 GB RAM,在Windows 7系统执行,以最大循环次数为结束条件。
3.2 实验一
针对小规模的车辆路径问题,选用文献[12-14]的案例,针对8 个顾客,1 个配送中心,车辆限额为8 t,顾客之间的距离矩阵如表1所示。
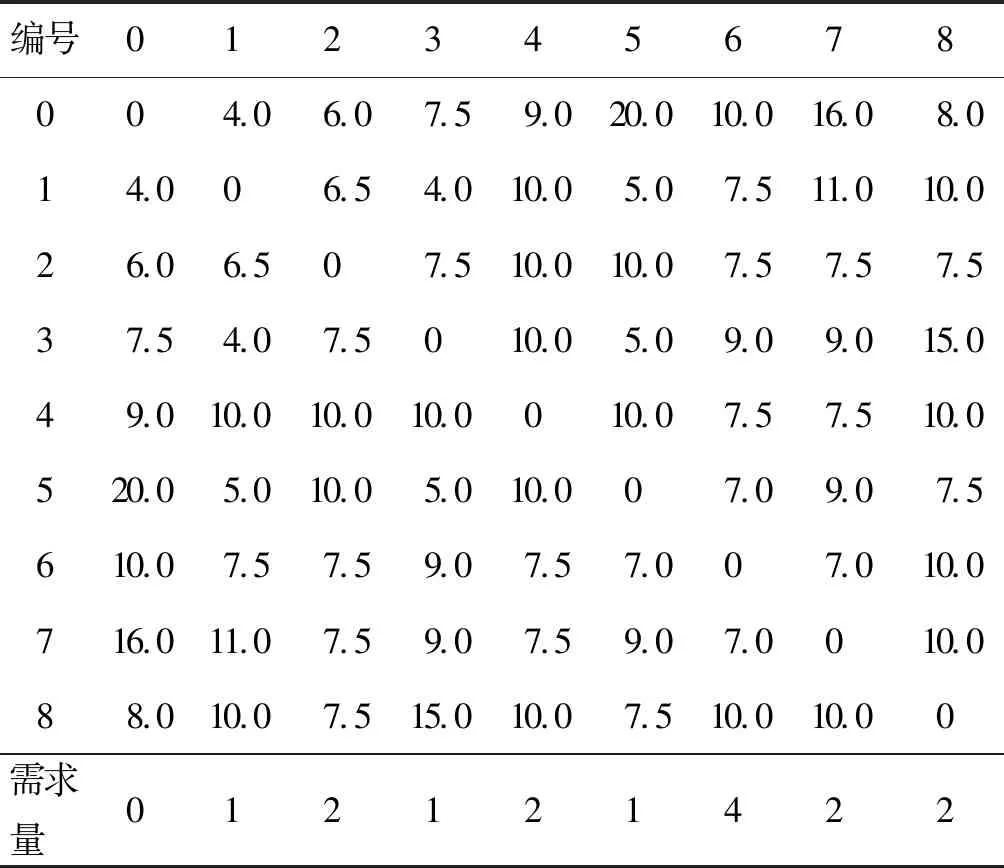
表1 中心与顾客距离及需求情况Table 1 Distance from depot center to customers
设置与文献[12-14]相同的种群数(种群规模=60)及最大进化代数(进化代数=50),将笔者提出的量子差分进化算法计算结果与其他启发式算法进行对比,结果如表2所示。由表2可知:在20 次的运算中量子差分进化算法以100%的次数获得最优解,相对于其他3 种算法,笔者算法的搜索性能更具有优势。
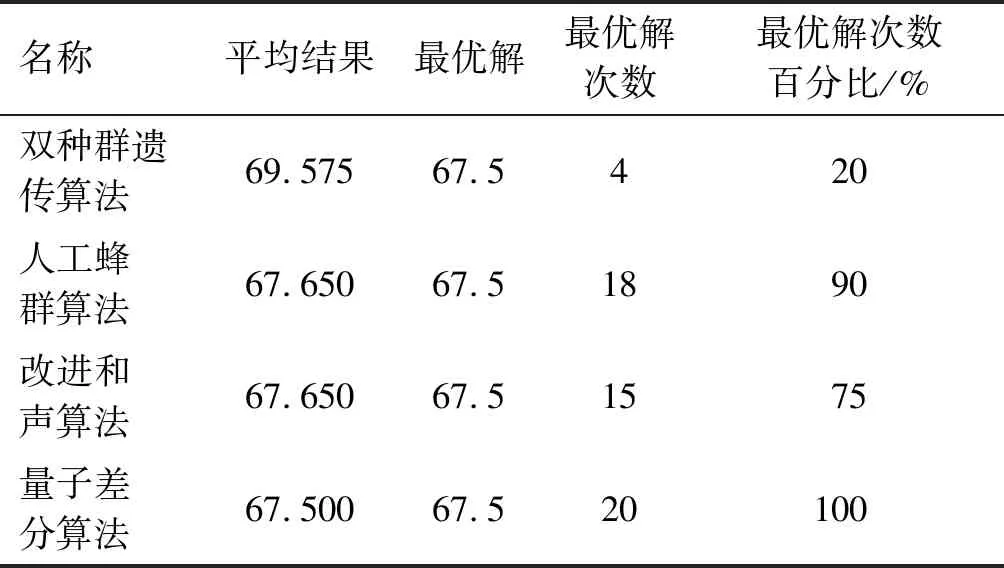
表2 量子差分算法与其他算法求解结果对比Table 2 Comparison for the performance of the proposed QDE algorithm
3.3 实验二
为了进一步测试算法性能,将笔者算法与标准CVRP进行对比,数据来源于http://Branch and cut.org/vrp/data/,每个案例计算10 次,以最大循环次数为结束条件,设置种群数为200,最大循环次数为500。将笔者算法与近3 年SC-ESA[15],CRO[16]和KmeansFnO[17]3 种新型算法最优解进行对比,比较结果如表3所示,表中第2列是标准算例结果,第3列是笔者算法的最优结果,4~6列为其他算法最优结果。

表3 QDE与其他3 种算法的标准算例结果对比Table 3 Comparison for the performance of the proposed QDE algorithm in benchmark
由表3可知:笔者算法在顾客数为19~22的P算例中均求得了与标准算例相同的解,说明笔者算法对小型规模算例的求解效果较好,相比较SC-ESA在同等问题中只有1 个解与标准算例相同,KmeansFnO有2 个解与标准算例结果相同,笔者算法对小型P问题算例的求解效果较好,在中型规模A算例中,QDE算法优于KmeansFnO但不及SC-ESA和CRO,对大型规模算例的求解效果不及其他3 种算法。
表4是量子差分进化算法、量子进化算法及差分进化算法的求解结果对比,表中3 种算法的种群均为200,最大循环次数均为500。
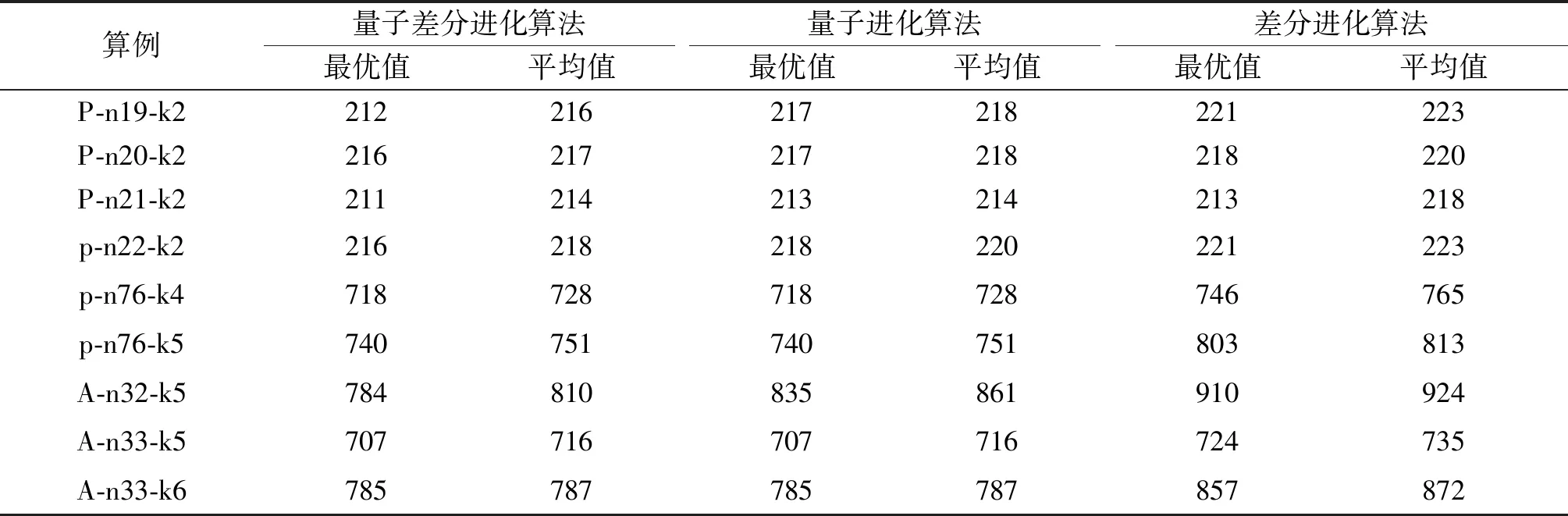
表4 量子差分进化算法与量子进化算法及差分进化算法结果比较Table 4 Comparison for the performance of the proposed QDE algorithm with QEA and DE
由表4可知:量子差分进化算法有56%(5/9)的算例最优值优于量子进化算法,有22%(2/9)的算例结果与量子进化算法相同,与差分进化算法相比,量子差分进化算法100%的结果优于差分进化算法,因此量子差分进化算法的求解效果整体优于量子进化算法及差分进化算法。
图3是P-n20-k2求解迭代过程与量子进化算法及差分进化算法的比较,图中实线为量子差分进化算法,虚线为量子进化算法,点线为差分进化算法。由图3可知:进化前期,3 种算法均能实现快速优化,相对而言,差分进化算法在进化前期的进化速度最快,但随着进化代数的增加,差分进化算法的搜索性能下降,最终的收敛解最差;量子进化算法的前期搜索效果较好,随着迭代次数的增加,其进化速度变慢;而量子差分进化算法结合其他两种算法的优点,在搜索后期持续优化,搜索到更好的解。因此,相对量子进化算法及差分进化算法,笔者算法在求解VRP问题时具有更强的全局搜索能力。

图3 进化过程对比Fig.3 Comparison for the evolution of the proposed QDE algorithm
4 结 论
设计了量子差分进化算法求解车辆路径问题,通过量子交叉、变异及动态量子旋转门实现量子种群的多样化进化。算法在典型实例求解中以100%的成功率获得最优解,优于双种群遗传算法、人工蜂群算法、改进和声算法;基于标准CVRP算例将笔者算法与CRO,SC-ESA,KmeansFnO 3 种新型算法进行对比,结果显示笔者算法对小型规模算例的求解效果优于SC-ESA及KmeansFnO,对中型规模算例的求解效果优于KmeansFnO但不及SC-ESA和CRO,对大型规模算例的求解效果不及其他3 种算法;与量子进化算法及差分进化算法的收敛对比实验显示笔者算法相对于其他两种算法具有更好的全局搜索能力。因此笔者算法是求解中、小型规模CVRP的一种有效算法,但对于大型规模CVRP问题,笔者算法求解效果一般,还需要进一步优化。
