时间透镜系统在流密码二次加密中的应用研究

(浙江工业大学 信息工程学院，浙江 杭州 310023)

密码学实质上是为了解决通信系统中信息传输和存储的安全性问题。密码学按照学科分类可以分为密码编码学和密码分析学，这两个分类形成了既独立又相对统一的矛盾体，安全的密码机制促使更强大的分析方法的发展，而强大的分析方法又推进更加安全的密码机制的诞生，两者在相互斗争中共同进步。根据密钥的不同，可以把密码学的研究分为分组密码和流密码。分组密码就是将明文信号分成固定长度的组块，随机使用同一密钥或算法对每一组块加密，每个输入块都会产生一个输出块，输出的信号也是固定长度的密文信号；流密码也被称作为序列密码，通过将明文信号按码元逐位加密[1]，并伴随着加密过程的进行，每次都产生一个密文的输出，即一次只加密一个比特或一个字节，美军的核心密码仍是一次一密的流密码体制[2]。

常用的流密码加密方式一般使用软件程序或者数字信号处理器来实现，但这些实现方式包括以下缺点：1) 通过软件程序和数字信号处理器对高速光信号加解密处理很困难；2) 传统的流密码加密方式需要使用大量硬件设备，其成本比较高昂[3]。由于“时间透镜成像系统”的提出和实现，可以通过时间透镜系统解决以上问题，基于四波混频的时间透镜成像系统在其放大倍数为-1时，经过时间透镜系统的光信号将发生时间反演，此过程和流密码加密系统中通过密钥对明文进行加密的过程相类似。考虑到时间反演一次加解密过程的安全性问题，在此基础上提出并验证了通过时间透镜成像系统对光信号进行二次加解密的可行性。

1 时间透镜成像系统的基本原理

时间域的色散传输方程和空间域的旁轴衍射传输方程形式相近，这种相似性称为光的时空二元性[9]。在空间域中，有空间光学器件如“棱镜”“透镜”的概念和成像理论，以光的时空二元性为理论基础，就可以推导出时间透镜成像系统包含输入色散装置、时间透镜、输出色散装置三部分。空间透镜系统中，其成像原理是空间透镜系统对空间二维坐标(x,y)产生二次相位调制，而在时间透镜中，其相位因子是φ(τ)=ω0τ2/(2fT)，式中fT是时间透镜系统的焦距，τ是时间域坐标。

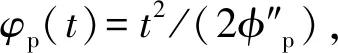
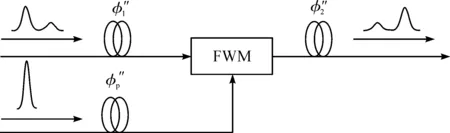
图1 四波混频时间透镜成像系统Fig.1 The structure of FWM time lens imaging system

图2 带有啁啾的泵浦脉冲与信号光的作用Fig.2 The effect of pump pulse with chirp and signal light

2 时间透镜成像系统在流密码中的应用研究

通过程序仿真设计可以使定量的码元在通过时间透镜成像系统时发生时间反演[7]，信号反演后即达到了加密目的，这就与流密码的加密过程相似。时间透镜成像系统应用于流密码加密系统的系统流程框图如图3所示。密钥流发生器会产生密钥k，可以控制泵浦脉冲的产生。明文的码元序列被划分成固定长度的基本编码码元，明文与泵浦脉冲在时间透镜系统中发生四波混频作用，明文信号的基本编码码元将发生时间反演或者波形不变。当密钥k为1时，会有泵浦脉冲的产生，码元将会发生时间反演；而当密钥k=0时，没有泵浦脉冲的产生，所以不会有时间反演发生。相反，反演信号再次通过时间透镜成像系统将实现信号的解密过程，这就将时间透镜成像系统应用在了难以实现的光信号实时加解密系统中。这里讨论的只是一次加解密过程[8]，其安全性并不好，容易被不法分子或非法机构捕获并破译信号，这就需要提出一种更加安全的流密码加解密方式。

图3 四波混频时间透镜加密系统框图Fig.3 Four-wave mixing time lens encryption system block diagram lens

一次加解密程序仿真时选择的各项参数分别是：信号1100101001010011为明文源，脉冲的宽度选择为5 ps，脉冲间隔为10 ps，输入光纤的二阶色散系数为20 ps2/km长度选为1 km。泵浦光输入光纤的二阶色散系数为20 ps2/km，长度也为1 km。输出光纤的二阶色散系数为-20 ps2/km，长度同样为1 km，n的值取为4，密钥流为1001。16 位信号每4 位分为一组，共分为4 组，由密钥信号可知第1组和第4组将发生时间反演，第2组和第3组信号保持不变。这里使用MATLAB进行程序仿真，结果如图4所示。图4(a)为输入的信源信号1100101001010011，图4(b)为输入的泵浦脉冲信号1001，图4(c)为经过时间反演的密文信号0011101001011100，最后使用相同的密钥，图4(d)为恢复出来的信号1100101001010011。通过仿真，可以发现使用密钥流加密的信号码元发生了改变，实现了对流密码的加解密过程。

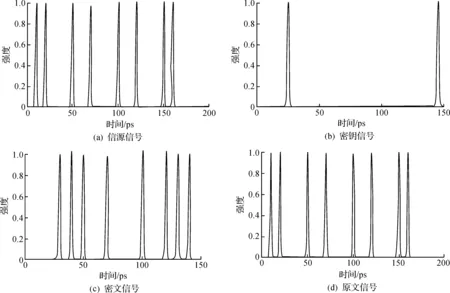
图4 多组信号进行加解密Fig.4 Encryption and decryption of multiple sets of signals

由于光信号一次加解密的复杂度不高，信息在传输过程中有可能会被截获和破解。为了克服现有技术中光信号加密度不够高、可能被不法分子窃取和破解的不足，这里提供了一种有效实现光信号二次加密与解密、安全性更高的基于时间透镜成像的光信号加/解密系统。该系统包括方阵排布子系统、行加密子系统、列加密子系统和方阵展开子系统。方阵排布子系统采用延迟技术将序列码原文排列为方阵码；行加密子系统采用密钥码对方阵码逐行进行加密获得新方阵码；列加密子系统采用密钥码对新方阵码逐列加密；方阵展开子系统再次利用延迟技术将方阵码展开，获得二维加密的序列密文。进一步，光信号二次加/解密系统有两个子系统，分别是加密子系统和解密子系统。

图5是二次加解密的整体系统构图，对原文序列通过延迟技术排布为矩阵码，时间透镜成像系统对矩阵按行进行随机反演，得到一次加密的密文序列，时间透镜成像系统再次对矩阵按列进行随机反演，得到二次加密的密文序列。最后，再次通过延迟技术将矩阵码转换为密文序列，即实现了对信号光的二次加密过程；反之，则可以实现对信号光的二次解密过程。这就把时间透镜成像系统成功地应用在了流密码二次加解密系统中，实现了安全性更高的加密方式。

二次加解密程序仿真时选择的各项参数分别是：信号1100101001010011为明文源，脉冲的宽度选择为5 ps，脉冲间隔为10 ps，输入光纤的二阶色散系数为20 ps2/km，长度选为1 km。泵浦光输入光纤的二阶色散系数为20 ps2/km，长度也为1 km。输出光纤的二阶色散系数为-20 ps2/km，长度同样为1 km，n的值取为4，密钥流为1001。16 位信号每4位分为一组共分为4 组，由密钥信号可知第1组和第4组将发生时间反演，第2组和第3组信号保持不变。泵浦脉冲发生器控制着泵浦信号的产生，这里产生的泵浦脉冲为1001，使用MATLAB进行程序仿真，结果如图6所示。图6(a)为输入信号1100101001010011，图6(b)为输入的泵浦脉冲信号1001，图6(c)是经过时间透镜成像系统时间反演后输出的一次密文信号0011101001011100，为了对列信号进行列加密处理，以此采用了延迟技术排布产生重新排布的一次密文信号，图6(d)即为经过延迟技术排布的一次密文信号，图6(e)为同样的密钥信号1001，图6(f)为再次经过时间透镜加密的二次加密信号1010001111000101，反之即是二次解密过程。通过仿真，可以发现使用密钥流加密的信号码元发生了改变，实现了对流密码的二次加解密过程。二次加解密过程相比于前面的一次加解密过程而言，很难被捕获和破译，更适合应用于对安全性要求较高的通讯场合。

图5 流密码二次加解密流程图Fig.5 Flow password secondary encryption and decryption flow

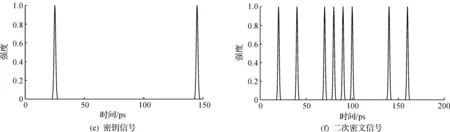
图6 多组信号进行二次加密Fig.6 Secondary encrypting multiple sets of signals

3 结 论

时间透镜成像系统可应用在高速光信号的加解密过程中，通过MATLAB程序仿真，当时间透镜的放大倍数为-1时，输入时间透镜系统的信源信号会发生时间反演，因此实现了对高速光信号的加解密过程。基于此理论提出的一次加密过程存在容易被破译的安全隐患，在时间透镜对流密码一次加密的基础上，进一步讨论了时间透镜成像系统对流密码二次加密的可行性，最后通过程序仿真实现了对高速光信号的二次加解密。