高墩大跨矮塔斜拉桥结构体系及静力性能研究

(浙江工业大学 建筑工程学院，浙江 杭州 310023)

矮塔斜拉桥亦称部分斜拉桥，是介于连续梁(刚构)与斜拉桥之间的一种桥型，具有刚柔并济、外观独特和结构灵活等特点[1-2]。矮塔斜拉桥总体上具有塔高较矮、主梁较刚和拉索相对集中的特点，主梁承担大部分荷载，拉索仅起辅助作用，兼具斜拉桥的柔性和连续梁桥的刚性，结构性能介于两者之间，填补了梁式桥和斜拉桥之间的跨径空白，为桥梁结构的发展提供了更广阔的空间。矮塔斜拉桥凭借其独特的结构形式和良好的受力特性，近些年在国内外得到迅速发展。

矮塔斜拉桥为高次超静定结构，整体结构受力状态主要取决于主梁刚度、斜拉索布置长度、桥塔高度和刚度及结构形式、边主跨比等结构参数。众多学者结合国内矮塔斜拉桥工程开展了结构受力性能及设计参数影响分析，揭示了矮塔斜拉桥的结构力学特点及其合理的设计参数取值[3-10]。当前，国内最大跨度的预应力混凝土矮塔斜拉桥为2014年建成的长山大桥，跨径为260 m，此外相关资料统计表明我国已建成的矮塔斜拉桥桥墩高度普遍低于100 m[2]。本研究的工程背景洪溪特大桥是一座主跨265 m预应力混凝土矮塔斜拉桥，该桥位于深切峡谷，桥墩高达142 m，桥面距离地面最大高差达250 m，是一座典型的高墩大跨矮塔斜拉桥。目前，国内外对高桥墩大跨矮塔斜拉桥的结构静力性能研究比较匮乏，特别是合理的结构体系方面。为此，结合洪溪大桥，采用MIDAS/Civil有限元分析软件，分析主梁高度、边主跨比、塔根无索区长度、跨中无索区长度(边跨无所区长度)、桥塔高度、桥塔刚度、桥塔形式、斜拉索布置形式和桥墩刚度等主要结构设计参数对高墩大跨矮塔斜拉桥结构静力性能的影响，探讨其经济合理的结构形式，为高墩大跨矮塔斜拉桥的设计提供参考。

1 桥梁简介

如图1所示为主跨265 m预应力混凝土矮塔斜拉桥方案，左右幅分离布设，桥跨布置为150 m+265 m+150 m，采用墩、梁、塔固结的结构体系，在桥台处设置纵向活动支座。主梁采用单箱双室变梁高预应力混凝土箱梁，梁宽15.25 m，中心梁高为4.5～9.2 m，梁底曲线为1.6 次抛物线。索塔采用双柱型混凝土塔，高约172 m，其中桥面以上塔柱高42 m，下塔柱采用空心薄壁墩，中间部分采用横桥向Y形薄壁墩过渡到上塔柱。斜拉索采用双索面半扇形稀索布置方式，在主梁上设置锚固横梁连接主梁和斜拉索，全桥梁共设置64 对斜拉索。边中跨拉索对称布置，塔根无索区主梁长度45.5 m，边跨端部无索区梁长29.2 m，中跨跨中无索区梁长24 m。

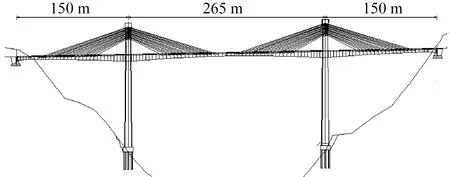
图1 洪溪大桥总体布置图Fig.1 General layout of the Hongxi bridge

该桥的主要设计标准：设计基准期为100 年；工程安全等级为一级；公路等级为高速公路，双向4 车道；设计车速为80 km/h；桥梁设计荷载为公路-I级；地震烈度为设计基本地震加速度为0.05 g，设防烈度Ⅵ度。

2 结构三维有限元模型

采用MIDAS/Civil有限元分析软件建立如图2所示的三维有限元分析模型，全桥共划分为549 个单元，432 个节点，其中主梁和索塔采用空间梁单元模拟，斜拉索采用桁架单元进行模拟。桥面主梁采用鱼骨式计算模型，主梁的刚度和质量集中在中间梁单元上，中间梁单元与两侧斜拉索采用刚臂单元连接。结构的约束信息：桥塔底部与承台顶面嵌固，即桥塔底部6 个方向自由度均约束；两侧桥台处主梁沿桥纵向、绕竖轴和横轴转动均自由，其他自由度约束；塔梁结合处固结，采用刚域处理。

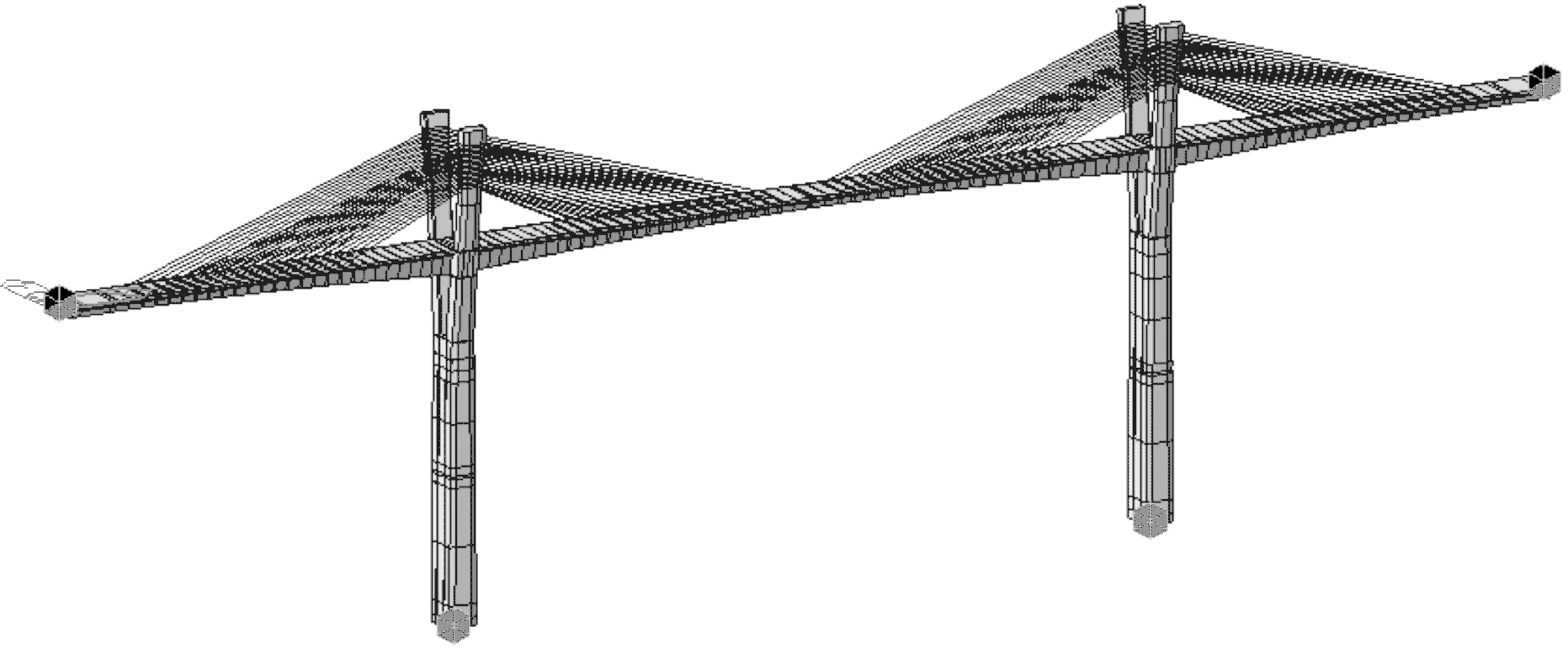
图2 结构三维有限元模型Fig.2 Structural 3D finite element model

3 高墩大跨矮塔斜拉桥结构静力特性分析

基于上述计算模型，首先采用MIDAS/Civil的“未知荷载系数”功能并控制各跨跨中竖向位移和塔顶水平位移为±0.01 m，计算各斜拉索的初始索力；其次，通过索力调整功能得到优化后的索力值；最后，通过结构在自重、二期恒载和优化索力共同作用下的几何非线性静力分析获得斜拉索最终的索力值及成桥状态结构的几何和内力状态，以此作为结构在运营状态荷载作用的基准态。

在计算的成桥状态上，考虑汽车荷载、汽车制动力、温度作用(体系升温或降温、非线性温度梯度)、主梁和桥塔的纵桥向和横桥向静阵风荷载等作用，进行结构几何非线性静力分析并进行最不利荷载效应组合，得到如表1所示的结构主要位移和内力的最大值，相应的结构位移和内力包络图如图3所示。分析时，汽车荷载按公路I级3 车道加载，并考虑汽车荷载横向折减和冲击效应影响；温度作用按体系升温25 ℃和降温-25.5 ℃考虑，同时考虑非线性温度梯度作用；考虑与汽车荷载组合，静阵风荷载计算时取桥面高度处的基准风速为25 m/s[11]。

表1 结构主要位移和内力值Table 1 Main structural displacements and internal forces

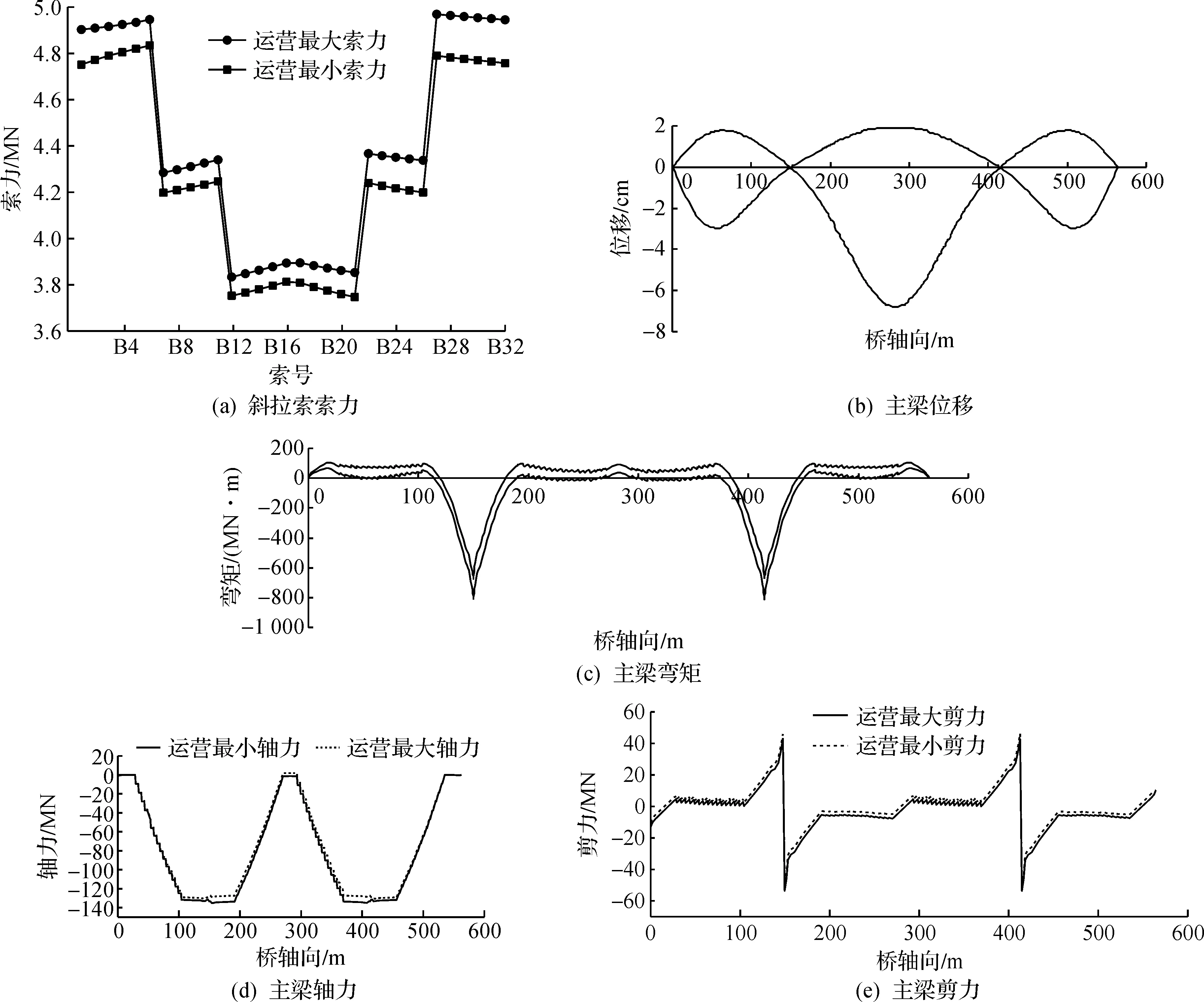
图3 结构位移和内力包络图Fig.3 The envelope diagrams of structural displacements and internal forces

由表1结果可知：主梁恒活载作用下的位移0.068 m，远小于规范对主梁最大竖向挠度L/500(0.53 m)的限值，同时桥塔的塔顶位移也很小，说明该桥具有很好的静力刚度。此外，该桥持久状况的主梁正截面和斜截面的抗裂性验算、塔墩的角点应力以及斜拉索的安全系数等均满足规范要求，说明结构设计方案合理。成桥状态恒载和活载作用下，塔梁结合处主梁出现了较大的负弯矩，同时承受最大的轴向压力和剪力，是其受力的关键部位；桥塔的内力最大值出现在塔底，其次为塔梁结合部，因此在高墩大跨矮塔斜拉桥设计中应着重关注塔梁结合部和塔底等截面的细部构造和局部应力分析。

4 高墩大跨矮塔斜拉桥结构静力性能设计参数分析

为探讨高墩大跨矮塔斜拉桥经济合理的结构形式，以洪溪特大桥为工程背景，分析研究主梁高度、边主跨比、塔根无索区长度、跨中无索区长度、桥塔高度、桥塔刚度、桥塔结构形式、桥墩刚度以及斜拉索布置形式等主要设计参数对结构静力性能影响及其合理取值范围。参数分析时，首先根据设计参数的变化调整结构布置建立对比方案桥并建立其三维有限元分析模型；其次确定其合理成桥状态；最后考虑结构自重、索力、二期恒载、汽车荷载、温度作用及静风荷载的共同作用，在计算得到的合理成桥状态上进行结构静力几何非线性分析，获得结构的位移和内力最不利值及其包络图。限于篇幅，下列参数分析只列表给出桥塔、主梁、桥墩和斜拉索的最不利的位移和内力值，值得注意的是表中桥墩最大弯矩一栏，*表示桥墩最大弯矩位置为Y字型墩分叉点处，未标明表示桥墩最大弯矩位置为墩底。

4.1 主梁高度

矮塔斜拉桥主梁在支点处的梁高一般为主跨跨径的1/39～1/32，跨中处梁高为主跨跨径的1/70～1/55，规范建议值为1/45～1/35[12]。设计方案桥支点处的梁高为跨径的1/28.8，跨中处梁高为跨径的1/58.9，可以看出方案桥支点处的梁高与其他桥梁相比较略微偏高。在设计方案桥基础上，将主梁跨中处和支点处的梁高分别调整为4.5 m与8 m、4 m与8 m，分析梁高变化对高墩大跨矮塔斜拉桥结构静力特性的影响，结果如表2所示。

表2 主梁高度对结构静力性能的影响Table 2 Effect of girder depth on structural static performance

从表2可以看出：高墩大跨矮塔斜拉桥主梁高度变化对桥塔和主梁弯矩和挠度影响较显著，但对斜拉索索力影响很小。在相同跨中梁高情况下，随着支点梁高的降低，主梁跨中挠度和塔顶水平位移增大，墩顶主梁弯矩和桥墩最大弯矩分别下降6.7%和4.5%，但主梁跨中弯矩增加6.5%。在相同支点梁高情况下，随着跨中梁高的减小，主梁跨中挠度和塔顶水平位移继续增大，主梁跨中弯矩和墩顶弯矩分别减小14.1%和4.8%，但桥墩最大弯矩增加14.7%。因此，相对于支点梁高，跨中梁高对高墩大跨矮塔斜拉桥的结构静力性能影响更显著。总体上看，主梁梁高变小，矮塔斜拉桥整体刚度减低，主梁受力减弱，斜拉索作用加强，桥墩受力变大，因此应结合结构的整体刚度、主梁和桥塔的受力综合确定主梁跨中和支点梁高的最优组合。

4.2 边主跨比

矮塔斜拉桥边主跨比是一个重要参数，比例太小会导致边跨支点处出现负拉力，比例太大则边跨会出现较大的正弯矩，给斜拉索的调索和边跨的配束带来困难，矮塔斜拉桥的边跨与主跨跨径比值统计值为0.42～0.62，规范建议取为0.5～0.76[12]。在设计方案桥(边主跨比0.566)基础上，保持中跨长度不变，通过改变边跨现浇段长度来调整边跨长度，取边主跨比分别为0.5，0.6和0.65建立相应的对比方案桥，分析边主跨比变化对高墩大跨矮塔斜拉桥结构静力性能的影响，结果如表3所示。

表3 边主跨比对结构静力性能的影响Table 3 Effect of the side to main span ratio on structural static performance

从表3可以看出：高墩大跨矮塔斜拉桥边主跨比对结构的刚度、边跨和中跨的主梁以及桥塔的受力有着显著的影响。随着边主跨比的增大，边中跨的主梁挠度和桥塔的水平位移均明显增大，尤其是边跨挠度增幅达178%，说明结构的整体刚度减小；主梁的边跨弯矩和桥塔弯矩成倍增加(增幅分别达936%和131%)，斜拉索索力也显著增大(增幅达10.3%)，主梁墩顶弯矩略有所增大，但其跨中弯矩却显著减小，减幅达70%。因此，边跨长度增加会明显增大边跨和桥塔的受力，并严重削弱结构刚度。从总体上看，设计方案桥的边主跨比较为合理。因此从结构静力性能考虑，高墩大跨矮塔斜拉桥宜采用短边跨，边中跨比为0.5～0.6比较适宜，尤其在0.55附近。

4.3 塔根无索区长度

如图4所示，设计方案桥边跨端部无索区长度L2=29.2 m，塔根无索区长度L1=45.5 m，中跨跨中无索区长度L3=24 m。塔根无索区长度与主跨的比值一般为1/9～1/4.5，规范建议值为0.15～0.2[12]。在设计方案桥基础上，保持边跨端部无索区L2、中跨跨中无索区L3、塔高及斜拉索在主梁上的布置间距与倾角不变，通过改变塔根处的斜拉索根数来改变塔根无索区长度L1，建立了塔根无索区长度L1分别为40.5 m和50.5 m的两座对比方案桥(单侧塔柱锚固的斜拉索数量分别为17 对和15 对)，其与主跨跨径比值分别为0.15和0.19，塔根无索区长度对高墩大跨矮塔斜拉桥结构性能的影响如表4所示。

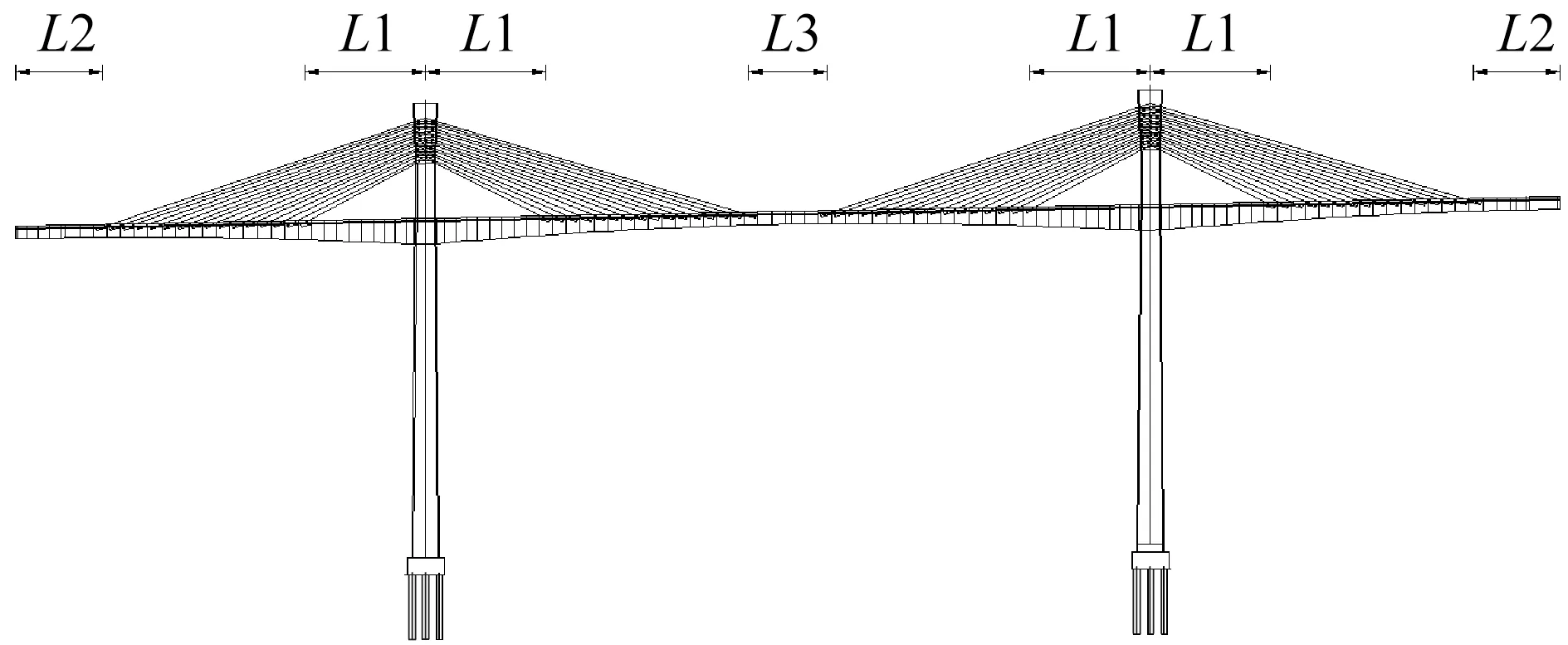
图4 无索区长度示意图Fig.4 The schematic diagram of non cable-stayed girder length

表4 塔根无索区长度对结构静力性能的影响Table 4 Effect of the non cable-stayed girder length near the towers on structural static performance

从表4可以看到：塔根无索区长度对结构位移基本没有影响，但对主梁和桥塔的受力影响显著。随着塔根无索区长度的增加，索力逐渐增加，但是增幅很小，越靠近塔根索力增幅越大；由于斜拉索承担的塔根主梁自重比例降低，主梁承受的弯矩增大，墩顶主梁弯矩增大36%，跨中处增幅则较小，约为3.7%；桥墩承受弯矩则减小，减幅达13.3%。总体上看，塔根无索区长度对墩顶主梁最大负弯矩影响明显，采用较小的塔根无索区长度对结构受力比较有利。

4.4 中跨跨中无索区(边跨端部无索区)长度

矮塔斜拉桥主跨跨中无索区长度L3一般为主跨长度的1/9～1/4.5，边跨端部的无索区长度L2一般为边跨长度的1/4.3～1/3，规范建议取值分别为中跨和边跨跨径的20%～35%[12]。在设计方案桥基础上，保持塔根无索区长度L1、塔高及斜拉索在主梁上的布置间距与倾角不变，通过改变斜拉索根数来改变边跨端部无索区长度L2和中跨跨中无索区长度L3，建立了两座对比方案桥，其边跨无索区长度L2分别为44.2 m和49.2 m，相应的跨中无索区长度L3分别为54 m和64 m，单侧塔柱锚固的斜拉索数量分别为13 对和12 对，中跨跨中无索区长度对高墩大跨矮塔斜拉桥结构静力性能的影响如表5所示。

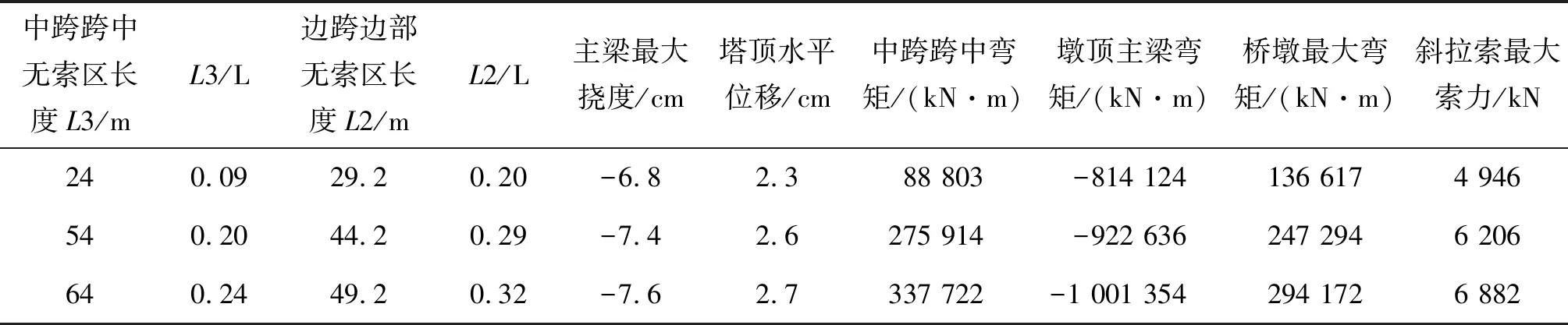
表5 中跨跨中无索区长度对结构静力性能的影响Table 5 Effect of the non cable-stayed girder length at midspan on structural static performance

从表5可以看出：中跨跨中无索区(边跨端部无索区)长度的变化对结构位移、主梁、桥塔和斜拉索索力的影响非常明显。随着中跨跨中无索区(边跨端部无索区)长度增加，由于斜拉索数量的减小，导致斜拉索索力增幅较大，最大索力增加49%；中跨跨中位移增大11%，塔顶水平位移增大17%；中跨跨中弯矩增加280%，墩顶主梁弯矩增加23%；桥墩最大弯矩增加115%。与前述塔根无索区长度因素相比，中跨跨中无索区(边跨端部无索区)长度对高墩大跨矮塔斜拉桥结构性能的影响更加显著，采用越小的中跨跨中和边跨端部无索区长度对结构整体受力越有利。

4.5 桥塔高度

如图5所示，此处的桥塔高度主要指桥面以上部分的高度，其与主跨跨径的比值一般为1/13～1/8.5，规范建议取值为1/12～1/8[12]。为研究高墩大跨矮塔斜拉桥塔高变化对结构静力性能的影响，在保持桥跨跨径布置、主梁和斜拉索布置不变的前提下，改变塔柱无索区高度h从而改变桥塔高度，建立塔高分别为66，33，26 m三座对比方案桥，计算结果如表6所示。

图5 塔高示意图Fig.5 The schematic diagram of tower height

表6 桥塔高度对结构静力性能的影响Table 6 Effect of the tower height on structural static performance

从图6可以看出：桥塔高度对高墩大跨矮塔斜拉桥的结构位移以及主梁、桥塔和斜拉索的受力影响非常显著。随着桥塔高度降低，斜拉索的竖向支撑减弱，从而导致索力的显著增加，当塔高从66 m降至26 m，最大索力增大近1倍；主梁最大挠度增大44%，塔顶水平位移降低约40%；主梁中跨跨中弯矩增加370%，墩顶弯矩增加322%；桥墩最大弯矩也成倍增大。总体上看，矮桥塔对结构受力十分不利，为改善高墩大跨矮塔斜拉桥的结构静力性能，建议采用较大的塔高跨比。

4.6 桥塔刚度

设计方案桥塔柱顶部截面尺寸为9 m(顺桥向)×3.5 m(横桥向)，由顶端往下线性地变化至主梁顶面处7.35 m(顺桥向)×3.91 m(横桥向)。为研究桥塔刚度对高墩大跨矮塔斜拉桥静力性能的影响，改变塔柱顶端截面尺寸为6 m×3 m，并由顶端往下线性地变化至设计方案桥主梁顶面处的塔柱尺寸，以反映桥塔刚度减小后高墩大跨度矮塔斜拉桥的结构静力特性，结果如表7所示。

表7 桥塔刚度对结构静力性能的影响Table 7 Effect of the tower stiffness on structural static performance

从表7可以看出：桥塔刚度减小后，主梁挠度和塔顶水平位移略微增大，主梁跨中处和墩顶处弯矩有所增大，增幅分别为3.2%和2%，桥墩最大弯矩略微减小，减幅为1.47%。因此，桥塔刚度因素对高墩大跨矮塔斜拉桥结构静力性能影响不明显，同时增大桥塔刚度更为有利。

4.7 桥塔结构形式

此处定义的桥塔结构形式主要是指桥塔的横桥向结构布置方式。设计方案桥的横桥向塔型为Y型，主梁以上部分塔柱向外侧倾斜。为研究桥塔结构形式对高墩大跨矮塔斜拉桥结构静力性能的影响，将主梁以上塔柱改为H型和倒V型布置方式建立对比方案桥，即桥塔横桥向两侧塔柱分别为竖直和向内侧倾斜，分析结果见表8。从表8可以看出：桥塔结构形式对结构位移和斜拉索索力影响甚微，改为H型和倒V型后，主梁跨中处和墩顶处弯矩略有增大，桥墩最大弯矩有所减小，但幅度都非常小。因此，桥塔结构形式改变对高墩大跨矮塔斜拉桥结构静力性能的影响不大，不是敏感因素。

表8 桥塔结构形式对结构静力性能的影响Table 8 Effect of the tower structural form on structural static performance

4.8 桥墩刚度

为研究桥墩刚度对高墩大跨矮塔斜拉桥结构特性的影响，将设计方案桥的桥墩尺寸缩小为原来的80%和70%建立对比方案桥，其他部位尺寸不变，分析结果见表9。从表9可以看出：桥墩尺寸下降至原来的70%时，即刚度下降后，主梁中跨跨中挠度增加41%，塔顶水平位移增加39%；主梁跨中处弯矩增大11.8%，但墩顶处弯矩增加很小，桥墩最大弯矩降低61%；斜拉索索力有微小增加，但可忽略不计。总体上看，桥墩刚度减小，主要影响为降低高墩大跨矮塔斜拉桥的整体刚度，略微增大主梁的受力，但可显著降低桥墩的受力程度。

表9 桥墩刚度对结构静力性能的影响Table 9 Effect of the pier stiffness on structural static performance

4.9 斜拉索布置形式

斜拉桥常用的索面布置形式为辐射形、扇形和竖琴形等，设计方案桥斜拉索采用扇形索面布置形式。为研究斜拉索索面布置形式对高墩大跨矮塔斜拉桥结构静力性能影响，通过降低塔根处无索区高度，保持其他参数不变，将设计方案桥索面布置改为竖琴形建立对比方案桥，计算结果见表10。

表10 斜拉索布置形式对结构静力性能的影响Table 10 Effect of the cable arrangement on structural static performance

从表10可以看出：当斜拉索布置形式改为竖琴形后，由于斜拉索倾斜角度的减小，斜拉索索力有所增加，最大索力增加6%。同时，由于斜拉索竖向支撑减弱，主梁挠度和弯矩均增大，尤其是墩顶主梁负弯矩增大近45%，桥墩最大弯矩也增大约9.7%。因此，斜拉索布置形式从扇形改为竖琴形后，由于斜拉索倾斜角度减小后其竖向支撑效果弱化，结构整体刚度下降，斜拉索、主梁和桥塔的受力增加，结构静力性能恶化。因此，高墩大跨矮塔斜拉桥不适宜采用竖琴形的索面布置形式，宜采用扇形布置形式。

5 结 论

以主梁挠度和塔顶水平位移、主梁跨中和墩顶处弯矩、桥墩最大弯矩和斜拉索最大索力等结构静力性能为指标，分析研究主梁高度、边主跨比、塔根无索区长度、跨中无索区长度、桥塔高度、桥塔刚度、桥塔结构形式、桥墩刚度以及斜拉索布置形式等设计参数对高墩大跨矮塔斜拉桥结构静力性能的影响。为了提高其静力性能，高墩大跨矮塔斜拉桥应结合结构的整体刚度、主梁和桥塔的受力综合确定主梁跨中和支点梁高的最优组合；宜采用短边跨，边中跨比在0.55附近；宜采用较小的塔根、中跨跨中和边跨端部无索区长度；宜采用较大的塔高跨比并增大桥塔刚度；减小桥墩刚度；斜拉索宜采用扇形布置形式。