基于小波的呼吸机管路积液自动检测算法研究

潘 清，马 树，张华青2，徐志江

(1.浙江工业大学 信息工程学院，浙江 杭州 310023；2.浙江大学医学院附属 第二医院 临床医学工程部，浙江 杭州 310009)

呼吸机是重症监护室(Intensive care unit, ICU)中最重要的生命支持设备。正确合理使用呼吸机可为呼吸衰竭的患者提供良好的机械通气支持，确保患者摄入充足的氧气，为医护人员抢救其生命提供宝贵时间[1]。但是，如果呼吸机使用不当则可能会引起肺损伤[2](Ventilator-induced lung injury, VILI)，并产生一系列相关并发症，如呼吸机相关性肺炎(Ventilator associated pneumonia, VAP)。呼吸机管路内的冷凝水和病人痰液积聚是VAP发生的重要原因之一[3]。首先，它会使管路内径缩小，增加气道阻力以及患者的呼吸做功，减少潮气量，当管路内大量积液时，患者有窒息的危险；其次，积液为病菌繁衍提供了环境，易导致肺部的二次感染，如出现肺炎等。呼吸机管路内积液的原因很多，包括护理人员专业知识的缺乏，未及时整理呼吸机管路和管路放置不合理，未及时倾倒接水杯，湿化灌过满等。尽管这些问题大多可通过加强培训和管理得到改善，但由于ICU内医患比例较低，护士工作量极大，呼吸机管路内积液未及时得到处理的情况普遍发生。因此，自动检测呼吸机管路内积液对降低患者发生并发症的风险、提升患者的治疗体验具有重要的价值。

呼吸机管路内存在积液的情况下，气道压力、流速波形呈现与正常情况显著不同的特征。因此，通过对压力、流速波形信号进行分析有望建立一种自动检测呼吸机管路内积液的方法。加州大学戴维斯分校的Adams等[4-5]通过对呼吸机波形的分析，在自动检测人机不协调方面取得了很好的效果，表明了基于呼吸机波形分析呼吸机使用的各种异常情况是可行的，但尚无基于呼吸机波形对管路积液进行自动化检测的报道。笔者提出了基于呼吸机压力波形的呼吸机管路积液自动检测算法。呼吸机管路积液情况下的压力波形特征具有较明显的时-频域特征，小波分析具有在时-频域上表征信号局部特征的能力，因此被广泛用于心电等生理时序信号的识别[6-9]和脉冲信号的检测[10]。因此，笔者选取了基于小波的方法对呼吸机波形进行分析。

1 小波分析理论

在呼吸机管路积液检测中，频域信息确定积液特征，时域信息能够确定积液产生于呼气相或者吸气相。小波变换对信号在时域和频域上进行局部变换，能够有效地提取信号的时-频信息，相比于传统的傅里叶变换无法时-频联合分析的缺点[11]，小波分析在时-频分析上具有显著的优越性。小波变换通过伸缩和平移等运算可对信号进行多尺度的细化分解，能够适应呼吸波形信号时-频分析的要求。利用小波分析对呼吸波形进行分解和重构，能够对波形中表征积液的特征信号进行提取和优化，提高积液检测的准确率。因此，笔者利用小波变换理论对呼吸机压力波形进行分析与研究。

1.1 连续小波变换

任何满足可容许性条件的L2(R)空间的函数f(t)在小波基下进行展开，这种展开函数f(t)的连续小波变换(Continuous wavelet transform，简称CWT)的表达式为

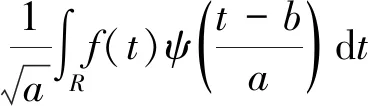
(1)

式中：WTf(a,τ)是小波变换系数；ψ(t)是小波母函数；a是小波基尺度；b是平移因子。小波连续变换是线性变换，一个信号的连续小波变换等于该信号分量的变换和。

小波变换可调节不同频率的信号在时域上的采样步长，其在低频部分有较高的频率分辨率和较低的时间分辨率，在高频部分有较低的频率分辨率和较高的时间分辨率[12]。小波分析中有很多的小波基函数，选取不同的小波基函数可以突出不同的信号特征。Daubechies小波是一种经典的常用小波基，一般表示为dbN，其中N是小波基的阶数。dbN小波在时域上是有限支撑的，在频域ψ(ϖ)上在ϖ=0处有N阶零点。

1.2 离散小波变换

呼吸机压力波形数据是采样频率为50 Hz的数字信号，为了适应数字信号处理，需要将连续小波变换离散化[13]。连续小波变换离散化的过程分为两步：首先，将连续小波变换的小波基尺度a离散化，得到二进小波变换；然后，将平移因子b离散化，就能得到离散小波变换。若小波函数ψ(t)满足

(2)

则称ψ(t)为基本二进小波。在连续小波变换式(1)中，令a=2k，得到二进小波变换，即

(3)

再将二进小波的变换中的平移因子也离散化，即令b=n2k，可以得到离散小波变换，即

(4)

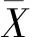
1.3 小波分解

离散小波变换可以看成是由低通滤波器和高通滤波器组成的一棵树。原始信号通过这对滤波器进行分解称为信号的一级分解。原始信号可以进行多级分解，如果停止对信号的高频分量的分解，而对信号的低频分量继续分解，就可以得到更多的低分辨率的低频分量。分解级数的多少需要根据待分析的信号特点确定。小波分解树表示对信号的低频分量进行连续分解，其结构如图1所示。

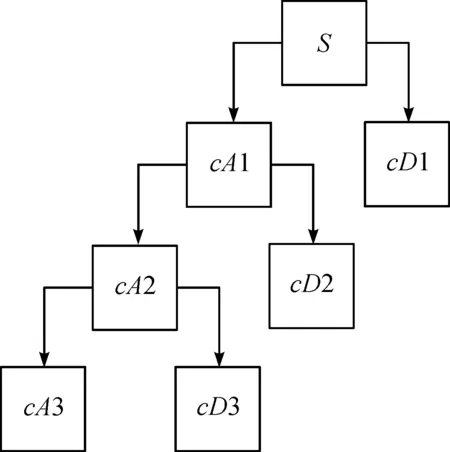
S—原始信号函数；c—系数；A—近似信号；D—细节信号。图1 小波分解树Fig.1 Wavelet decomposition tree

1.4 小波重构

小波分解得到的信号分量还原成原始信号的过程就是小波重构(Wavelet reconstruction)[14]。应用滤波器作小波变换时包含滤波和降采样两个过程，在小波重构时则需要有升采样和滤波两个过程[15]。小波重构的方法如图2所示。图中↑表示二元上抽样，它在一个向量中每间隔一个元素填充一个0元素，重新组成一个新向量。g0(n)和g1(n)称为综合滤波器。在小波分解后，将属于噪声的分量滤除，再重构信号，即可得到滤波后的信号。

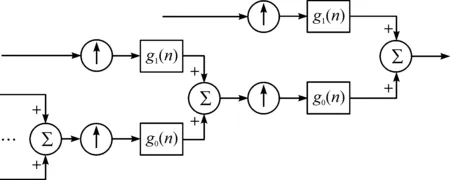
图2 小波重构Fig.2 Wavelet reconstruction

2 积液检测算法

2.1 积液检测算法总体设计

在呼吸机管路内存在积液的情况下，呼吸的压力波形中呈现较明显的高频波动噪声，因此笔者以呼吸压力波形为分析对象，检测呼吸机管路内存在积液的情况。图3是正常呼吸状态与呼吸机管路内发生积液情况下压力波形的对比。

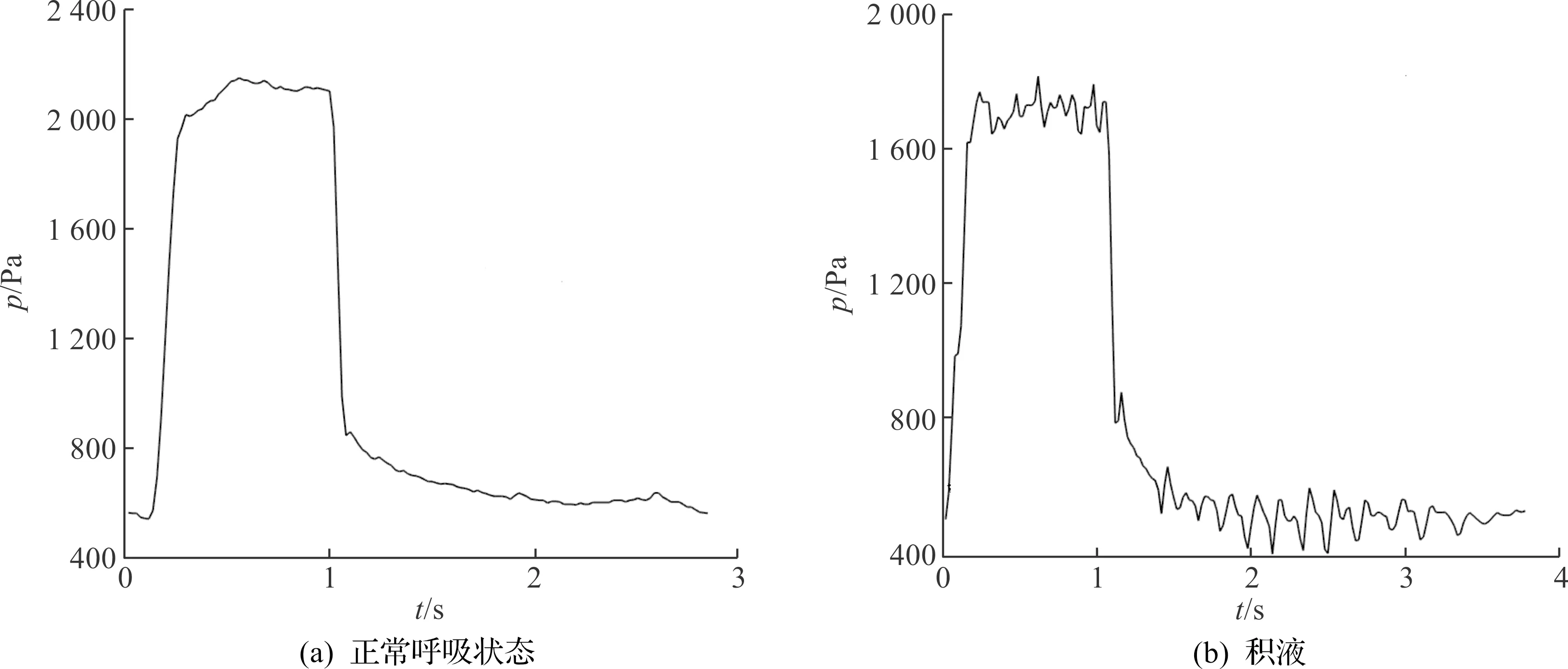
图3 正常呼吸状态与积液情况下呼吸压力波形Fig.3 Pressure waveforms under normal ventilation and with hydrops in the tube

呼吸机管路内积液的判定算法是基于每个呼吸周期进行设计的。呼吸机提供机械通气的方式是通过呼气管路和吸气管路进行的，呼吸机的使用过程中可能会出现呼气管路或者吸气管路产生积液的情况，且患者的吸气和呼气波形存在差异，如果忽视呼气相和呼气相的差异而统一进行阈值设置是不当的，会对实验结果产生影响，故笔者算法对每个呼吸周期中的吸气相和呼气相分别进行设计，其基本流程如图4所示。首先，以呼吸流速波形由正到负的过零点作为吸气相、呼气相临界点，分别用于判断呼气相或吸气相积液；然后，对呼吸压力波形进行小波分解，再对细节信号进行小波重构；最后，基于重构的信号分别对吸气相、呼气相进行阈值选择，以阈值判别是否存在积液，基于阈值的积液判断流程将在后面进行详细描述。

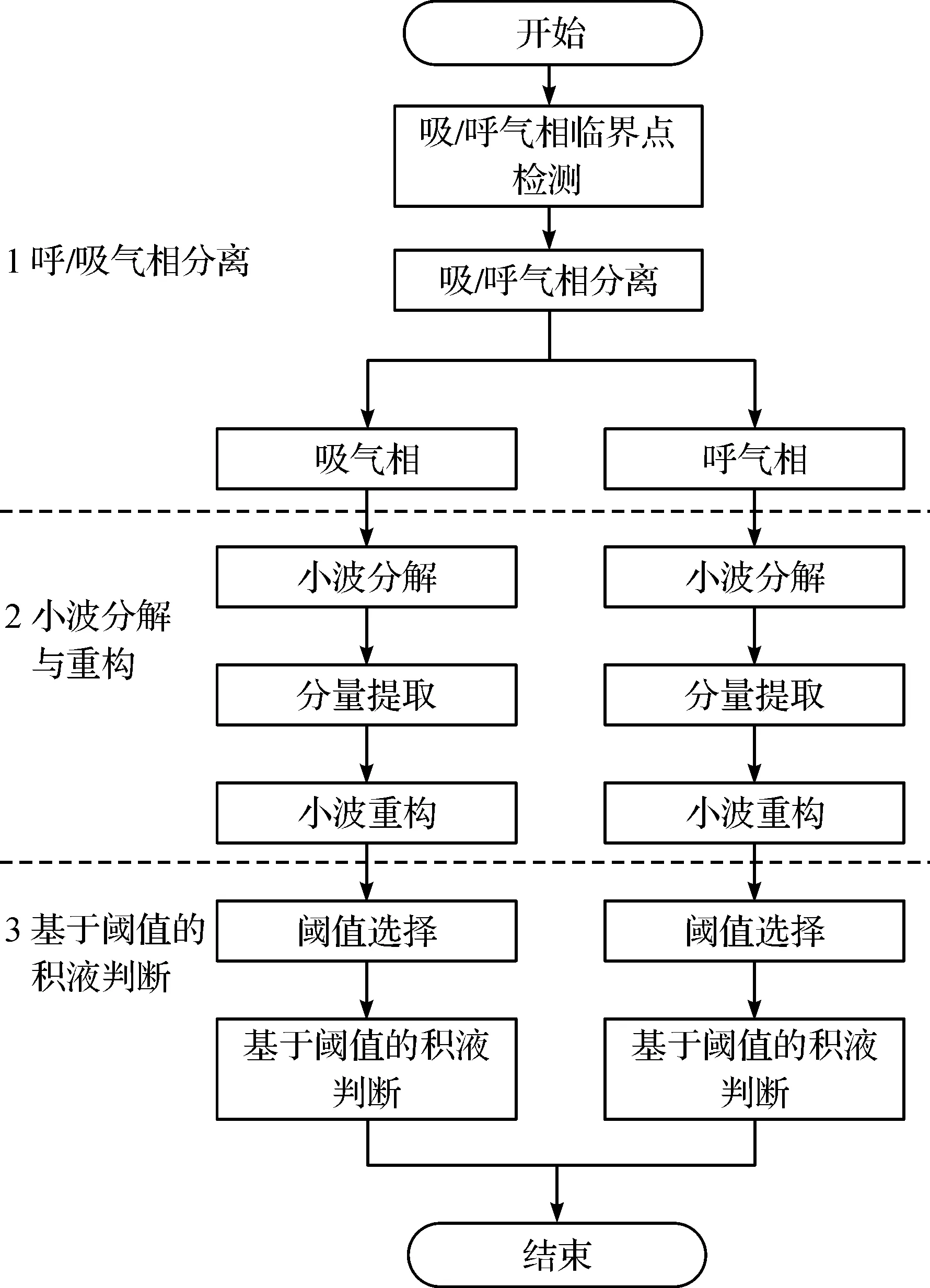
图4 呼吸机管路内积液判定流程Fig.4 Flowchart of the detection of hydrops in the ventilators

2.2 呼吸压力波形的小波分解与重构

根据Daubechies小波函数理论和呼吸机管路内积液情况下压力波形的特征，选择五阶Daubechies(db5)小波基对压力波形进行5 层分解，得到了近似信号a5与细节信号d1～d5一共6 组信号。图5是正常呼吸状态下的呼吸压力波形在db5小波5 层分解下得到的近似信号和细节信号图。图6是在呼吸机管路内积液情况下对压力波形进行db5小波5 层分解后得到的近似信号和细节信号图。从图6中可以看到：呼吸机管路内积液的特征信息主要分布在d1～d3层。

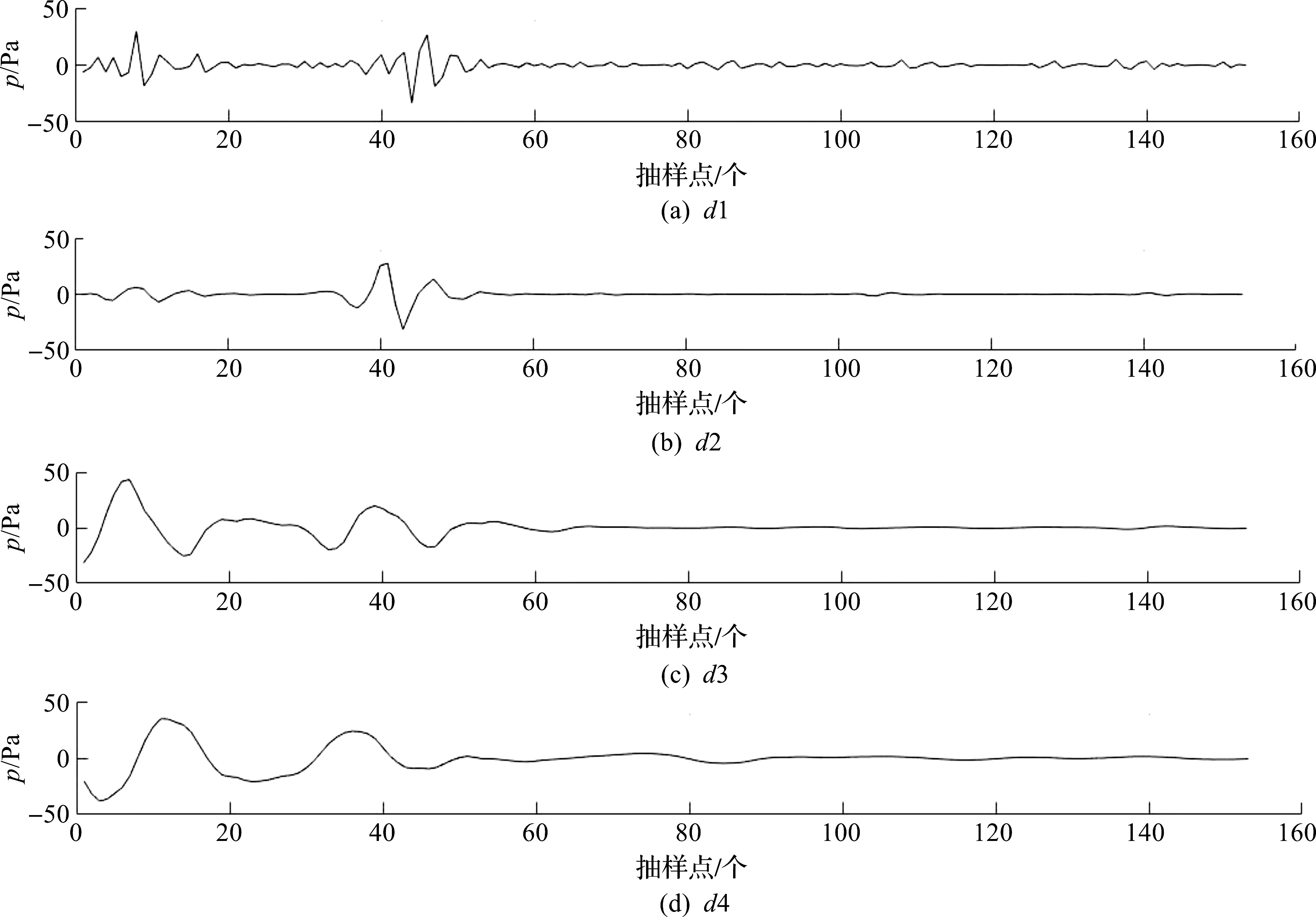
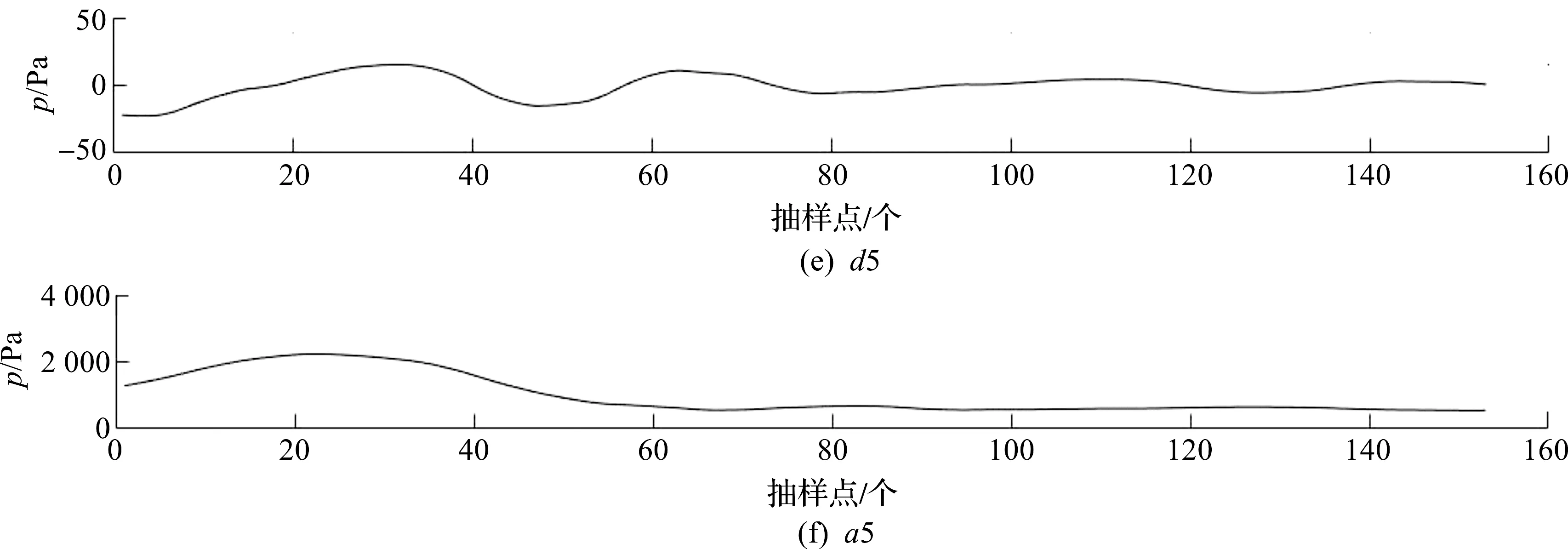
图5 正常压力波形db5小波5 层分解Fig.5 Five-layer wavelet decomposition of the pressure waveform based on db5 wavelet basis

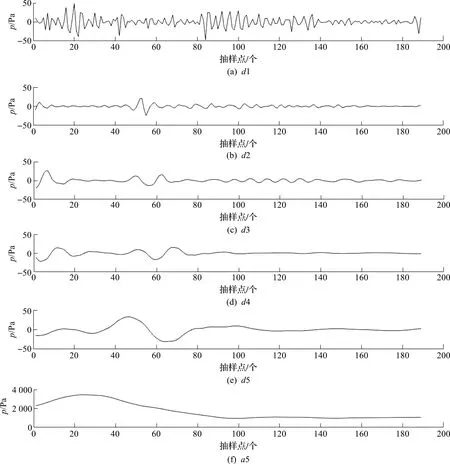
图6 积液压力波形db5小波5 层分解Fig.6 Five-layer wavelet decomposition of the pressure waveform with hydrops based on db5 wavelet basis

笔者测试了4 种信号重构方法，分别是利用d1，d2，d3进行构造，具体的构造方法如表1所示。表1中构造信号S4中的变量K取值为0.05，0.1，0.5，1.0，2.0。

表1 信号重构方法Table 1 Signal reconstruction methods

2.3 基于阈值的积液波形检测算法

重构信号S1～S4中包含了能够区分正常与积液情况下波形的特征信息，因此可以通过设定重构信号的阈值对积液波形进行检测。但是，由于不同患者的呼吸状态存在差异，甚至同一个患者的每个呼吸周期都会存在差异，因此阈值的选取需要考虑个体间差异与个体内差异。笔者提出了基于每个呼吸周期的阈值选取法：首先，对每个呼吸机压力波形采用db5小波基进行5 层小波分解；然后，计算重构信号的均值和标准差，以均值加标准差作为检测到积液的阈值。均值和标准差的求值公式为

(5)

阈值thr的计算公式为

thr=μ+std

(6)

式中：di为细节信号的每个采样点；μ为细节信号的均值；std为细节信号标准差。

针对每个呼吸周期波形设计积液特征分析算法，如果在连续多个呼吸波形上检测到积液特征，则确认积液存在，以避免因为患者咳嗽、翻身等动作引起的偶然性压力波形变化，其流程如图7所示。首先，定义整数n1，用来表示每个呼吸周期中重构信号大于阈值的点的数量，当n1大于3时判定当前呼吸周期满足阈值条件；其次，定义计数器n2，将其初始化为0，若当前呼吸周期满足阈值条件时，则n2=n2+1，若当前呼吸周期不满足阈值条件，则将n2置为0；最后，如果n2大于3，则计数器计数的n2个呼吸周期存在呼吸机管路内积液。图8是一个呼吸周期内吸气相和呼气相的阈值选定结果，图中横线代表的是选定的阈值。将上述方法逐个应用于每个呼吸机周期，利用受试者工作特征曲线(Receiver operating characteristic curve，ROC曲线)分析计算最优的积液波形检测阈值，并计算该阈值下的检测灵敏度、特异度和准确率。

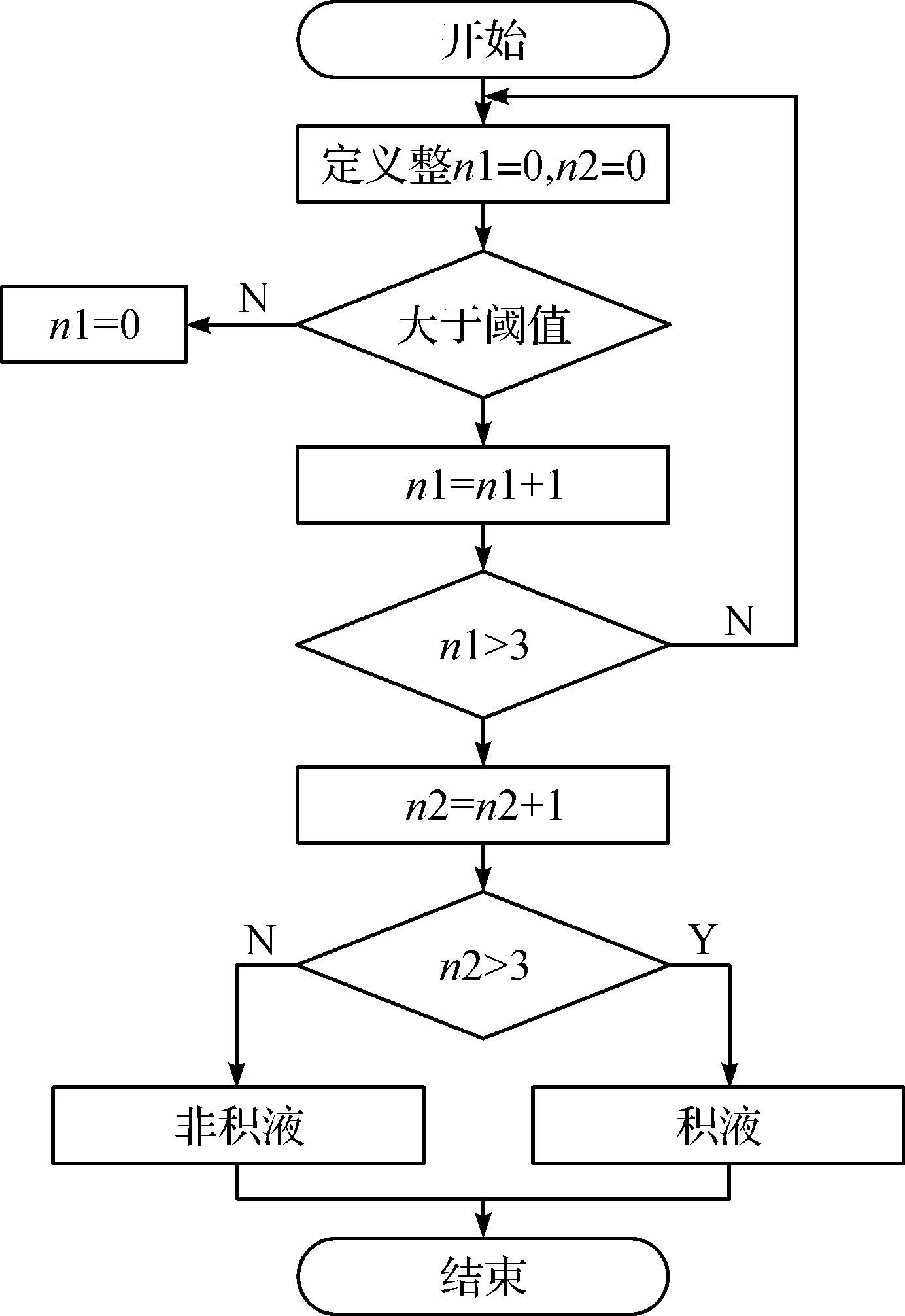
图7 基于阈值的积液判定流程Fig.7 Threshold-based hydrops determination process

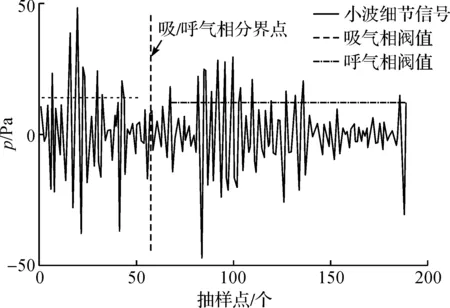
图8 阈值选定图Fig.8 Diagram of dynamic threshold selection

2.4 测试数据集

分别使用模拟肺数据和临床采集的真实病人数据对呼吸机积液波形检测算法进行测试。呼吸机采用泰科公司的PB840。表2给出了实验数据集的情况。使用医院内模拟肺来模拟人的呼吸，并在呼吸机吸气和呼气管路内加入蒸馏水模拟呼吸机管路内积液的情况，以获得模拟肺数据。模拟肺数据共包含163 个呼吸周期，其中双相积液59 例，无积液104 例。在59 例积液病例中包含了各种常用的呼吸机通气模式，在104 例无积液病例中包括了正常呼吸波形16 例，以及部分人机不协调波形(人机对抗呼吸波形14 例，双触发呼吸波形74 例)，用来检验算法的抗干扰能力。临床数据来自于浙江大学医学院附属第二医院心外科重症监护室，共包含3 例病人，1 161 个呼吸周期。其中呼吸机管路内积液共739 例(包括125 例双相积液，614 例呼气相积液)，无积液422 例，在管路内积液病例中包括614 例容控有压力支持和125 例压控有压力支持模式下的病例。422 例无积液波形均为正常呼吸波形。

表2 测试数据集样本数Table 2 Number of samples in the testing dataset

笔者在实验数据上进行5 折交叉验证，并取各次交叉验证结果的特异度和灵敏度平均值作为最终的实验结果。

3 结果分析

3.1 K值对性能的影响分析

首先基于临床数据中的双相积液样本分别检测吸气、呼气相积液情况，测试分析S4重构方法中K值对分类性能的影响。实验中K分别取0.05，0.1，0.5，1.0，2.0，并计算得到K取不同值时的ROC曲线下面积(Area under curve，AUC)。通过ROC曲线可以观察出不同阈值条件对积液的检测能力，ROC曲线越靠近左上角，其准确率就越高。笔者通过ROC曲线选择适当的阈值对压力波形进行积液的判断。一般用AUC值作为标准来评判分类器效果，AUC值越大则说明分类器的效果越好。表3是K取不同值时吸气相、呼气相积液检测的AUC值。

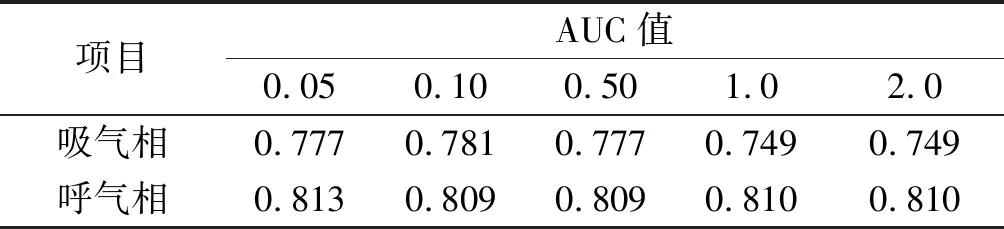
表3 K取不同值时吸/呼气相AUC比较Table 3 Comparison of AUC under the inspiration/expiration phase with different K values

从表3可以看出：在吸气相积液判定中，K=0.1时表现最优；在呼气相积液判定中，K=0.05时表现最优，但是与其他取值时的差距较小。试验时发现：当K取值为1.0，2.0时，吸气相、呼气相的AUC值没有变化，因此在后续的实验中K取值为0.1。

3.2 小波重构方法性能分析

笔者分别分析了不同小波重构方法对积液检测结果的影响，并以ROC曲线展示不同小波重构方法对积液的检测能力。图9展示的是S1，S2，S3，S4(K=0.1)时的吸气相ROC曲线，图10是呼气相ROC曲线，表4是S1，S2，S3，S4(K=0.1)时吸气相、呼气相的AUC值，图9，10和表4是五折交叉验证中一折的结果。从上述图表中可以看出：基于S1重构信号无论在吸气相还是呼气相都是能够得到最优的判别结果。在吸气相积液判定上的性能表现为S1>S4>S2>S3，在呼气相积液的判定上S1>S2>S4>S3。

图9 S1～S4吸气相ROC曲线Fig.9 ROC curves for the inspiration phase with the reconstruction signal of S1～S4

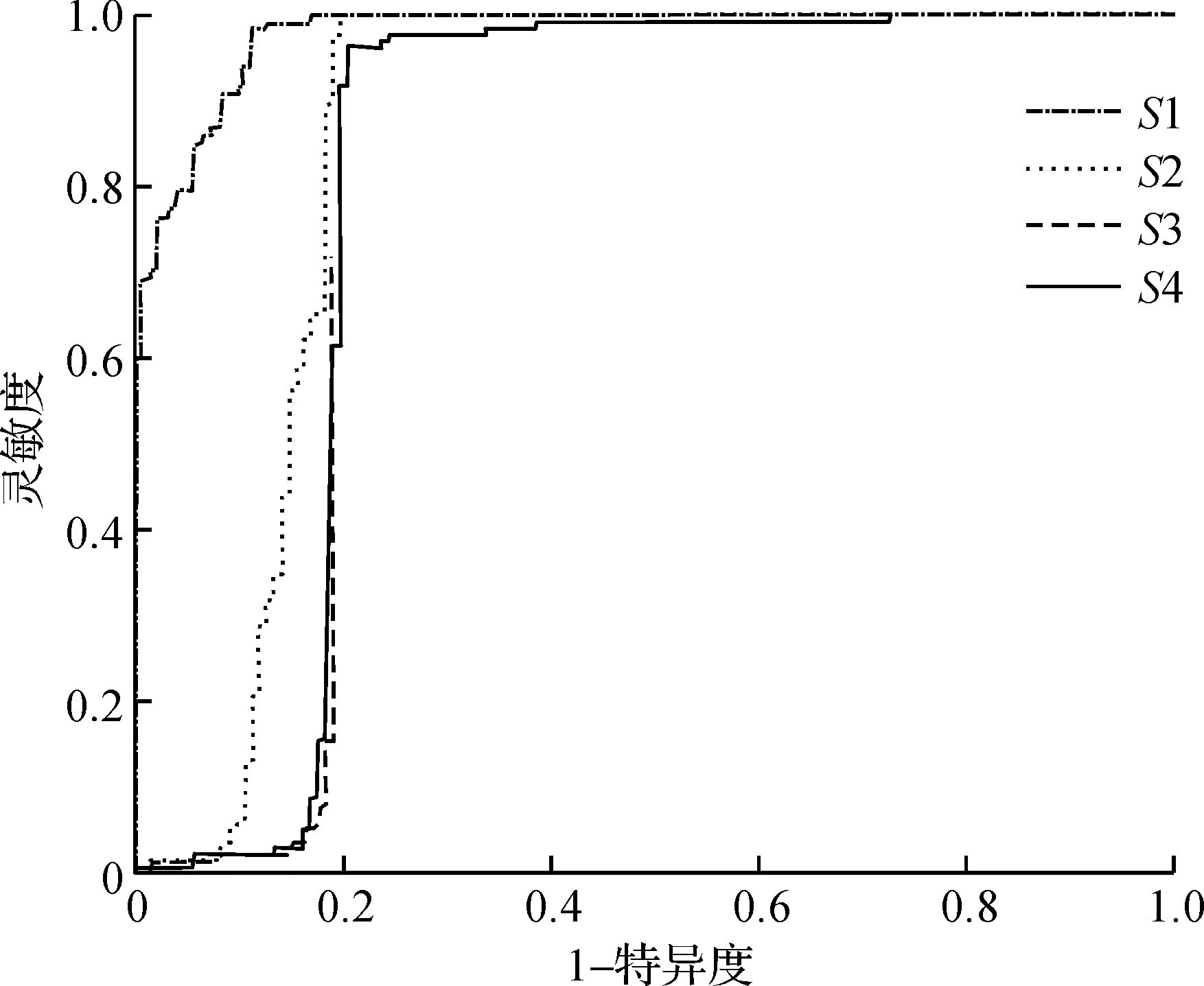
图10 S1～S4呼气相ROC曲线Fig.10 ROC curves for the expiration phase with the reconstruction signal of S1～S4

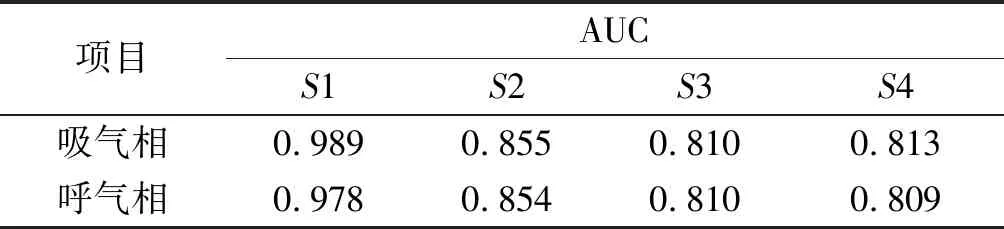
表4 S1～S4时吸/呼气相AUC比较Table 4 Comparison of AUCs during inspiration and expiration phase with the reconstruction signal of S1～S4

笔者分别基于模拟数据和临床数据进行了测试，验证在不同的小波构造方法下，呼吸机管路内积液检测的灵敏度、特异度和准确率。在验证结果的统计上，笔者的做法是在吸气相或者呼气相检测到有积液的情况发生则认定为呼吸机管路内积液。表5是在模拟数据上的验证结果，表6是在临床数据上的验证结果。

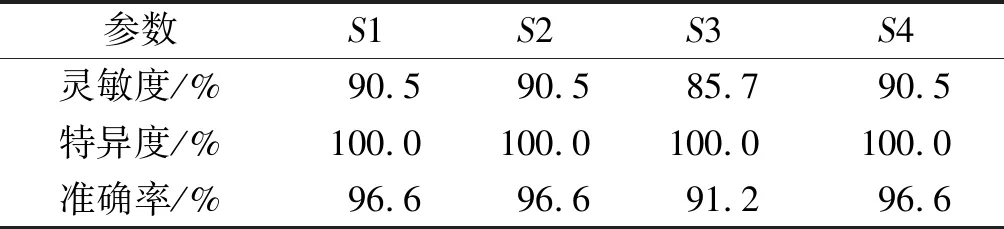
表5 模拟数据上的积液判定Table 5 Accumulation of water on simulated data

表6 临床数据上的积液判定Table 6 Accumulation of water on clinical data

表5，6中的灵敏度、特异度、准确率均为五折交叉验证的平均值。上述验证结果表明：在模拟数据的数量相对较少的情况下，S1，S2，S3，S4在灵敏度上的表现为S1=S2=S4>S3，准确率上的表现为S1=S2=S4>S3；临床数据上的测试结果表明小波构造法S1的判定效果最好，其灵敏度上的表现为S1>S2>S4>S3，准确率上的表现为S1>S2>S4>S3。

由实验结果可知：积液特征主要包含在d1层而非d2，d3层，S1重构方式仅对d1层细节信号进行重构，而其他重构方式增加了d2，d3层细节信号，会增加非积液特征信号，对阈值设置产生影响，降低积液检测的准确性，但这也需要更多的数据加以验证。呼吸机管路内积液干扰因素较多，如患者的翻身、咳嗽等，都会对积液判断产生影响，导致类似于积液特征的波形出现，因此笔者在进行灵敏度和特异度选择上更倾向于特异度，并且从实验结果上看灵敏度的损失并不大，在可接受范围内。模拟数据是由医院提供的模拟肺产生的。在采集模拟数据的过程中，使用了多种呼吸机的控制模式，包括A/C(辅助/控制模式)、SIMV(同步间歇指令通气模式)、SPONT(自主呼吸模式)等，在A/C模式中又使用了压控模式和流控模式，因此模拟数据呼吸波形的多样性较高。而临床数据仅来自于3 例患者，尽管波形个数较多，但波形异常类型的多样性不高，因此出现临床检测效果优于模拟数据的情况。

4 结 论

基于小波多尺度分解的方法，提出了一种呼吸机管路内积液的判定方法，对呼吸机压力波进行小波分解，选择特征分量进行重构，以阈值检测积液的存在。通过ROC曲线分析几种信号重构方法的性能差异，最后通过对模拟数据和临床数据的验证，计算积液检测算法的灵敏度和特异度。研究结果显示：所设计的判定算法对于判定呼吸机管路内积液具有较高的准确率。尽管笔者提出的呼吸机管路积液检测算法具有很好的性能，但研究具有一定局限性，例如实验数据量较小，且对照样本类型较为单一，缺少其他异常呼吸波形的干扰，且对呼吸机管路积液波形特征信号的提取方式单一。今后的研究将采集更大规模、更多样性的样本，并尝试更好的积液体征提取方法，以进一步验证和改进算法的准确率。