Numerical Stability and Oscillation of a kind of Functional Differential Equations
2020-01-15WANGQiYAOJieyi
WANG Qi YAO Jie-yi
(School of Applied Mathematics,Guangdong University of Technology,Guangzhou 510006,China)
Abstract The paper focuses on the stability and oscillation of numerical solutions for a kind of functional differential equations.Firstly,the conditions of numerical stability and oscillation are obtained by using the θ-methods.Secondly,we studied the preservation behavior of numerical methods for the two dynamical properties,namely under which conditions the stability and oscillation of the analytic solution can be inherited by numerical methods.Finally,some numerical examples are given.
Key words Functional differential equations;θ-methods;numerical solution;stability;oscillation
0 Introduction
As a special kind of functional differential equations,the differential equation with piecewise continuous arguments (DEPCA) has aroused lots of attention.Various properties of DEPCA have been investigated deeply.Such as convergence[16],stability[4,11],oscillation[2],periodicity[1],bifurcation[3]and asymptotic behavior[5],etc.However,all papers mentioned above deal with the properties of analytic solution of DEPCA.Nowadays,it is worth noting that numerical analysis of DEPCA be of particular interest for many scientists.Some important properties such as numerical stability[8],numerical oscillation[6,7]and numerical dissipativity[15]were investigated.In recent two papers [9,17],the authors discussed numerical approximation of DEPCA in stochastic and impulsive case,respectively.In the case of PDE,some our contributions[12,13]maybe noted.Different from above cases,in the present work,we shall study both numerical stability and oscillation for a more complicated DEPCA with scalar coefficients,and get some new results.
In this paper we consider the following DEPCA
(1)
herea,b,care all real coefficients andu0is initial condition,[·] denotes the greatest integer function.In particularly,whenc=0,the equation in Eq.(1) becomesu′(t)=au(t)+bu([t]),which is exactly the case of [8].Ifb=0,the equation in Eq.(1) becomesu′(t)=au(t)+cu(2[(t+1)/2]),which is exactly the case of [10].Thus,the results in this paper are the generalization of corresponding ones in [8] and [10].The following results for the analytical stability and oscillation of Eq.(1) will be useful for the upcoming analysis.
Theorem1[14]The analytic solution of Eq.(1) is asymptotically stable for any initial value,if one of the following cases is true
(2)
and
(3)
Theorem2[14]Assume thata≠0,then Eq.(1) is oscillatory if and only if one of the following conditions is true
(4)
1 The discrete scheme
Seth=1/m(m≥1) be stepsize,we consider the linearθ-method to Eq.(1)
(5)
and the one-legθ-method to Eq.(1)
(6)
hereθ∈[0,1],un,uh([nh]) anduh(2[(nh+1)/2]) denote approximations tou(t),u([t]) andu(2[(t+1)/2]) attn,respectively.
Letn=km+l(l=0,1,…,m-1),we defineuh(tn+ηh) asukm,uh(2[(tn+ηh+1)/2]) asu2kmaccording to [8,10],where 0≤η≤1.Thus Eqs.(5) and (6) can be reduced to the same recurrence relation
(7)
It is easily seen that Eq.(7) is equivalent to the following two cases
(1) Ifa≠0,
(8)
(9)
(2) Ifa=0,
(10)
(11)
Theorem3 Assume thatλ≠0,then Eq.(1) has the numerical solution
(12)
fora≠0,wherel=0,1,2,…,m-1 and
and
(13)
fora=0,wherel=0,1,2,…,m-1 andλ=(b+1)(b+c+1)/(1-c).
ProofAssume thatunis a solution of Eq.(7) with conditionsu2jm=d2jandu(2j-1)m=d2j-1.It follows from (9) that
(14)
From (14) and (8) withl=m-1 we have
which implies that
(15)
hence
then ifa≠0 andλ≠0 we get (12).Formula (13) can be obtained in the same way.The proof is complete.
2 Stability and oscillation of numerical solution
Lemma1un→0 asn→if and only if |λ|<1,whereλis defined in Theorem 3.
Theorem4 The numerical solution of Eq.(1) is asymptotically stable for u0,if one of the following cases is true
(16)
and
(17)
ProofAccording to Lemma 1 and Theorem 3 we know that the numerical solution of Eq.(1) is asymptotically stable if and only if
(18)
fora≠0 and
(19)
fora=0.
Ifa≠0,from (18) we have the following two inequalities hold
which are equivalent to
so we can get (16).Ifa=0,similar to the case ofa≠0,we can get (17) from (19).
From Theorem 3 we have the following corollary.
Corollary1 Assume thata≠0 then
wheredj=ujmand satisfies (15).
It is easy to check that the following two lemmas are hold.
Lemma2 Sequenceul=-aαl/(αl-1) is strictly monotonic increasing forl=0,1,…,manda≠0.
Lemma3 Assume thatb+c>-aαm/(αm-1) holds,thenb+c>-aαl/(αl-1) holds forl=0,1,…,m-1 implies thatαl+(b+c)(αl-1)/a>0.
Theorem5 Assume thata≠0,then Eq.(7) is oscillatory if and only if any of the following conditions is satisfied
(20)
ProofSufficiency.It follows from (19) that the sequence {dj}oscillates under any of the condition (20).Sinceujm=djforj=0,1,…, sounalso oscillates.
Necessity.We assume that any of the following hypotheses is satisfied
(21)
Letunbe the solution of Eq.(7),then from (15) and (21) we havedj>0 forj=0,1,2,…. By Corollary 1,Lemmas 2 and 3 we get
(1) Forn=2jm+landj=0,1,2,…
(2) Forn=(2j-1)m+landj=1,2,…
So we know thatunis a monotonous sequence forn=(2j-1)m+l.On the other hand,u(2j-1)m+m=d2jatl=m,sounhas the minimum valued2jord2j-1forn=(2j-1)m+l,namely
un≥min{d2j-1,d2j}>0.
Combining (i) with (ii),we obtainun>0 forn=km+l.This contradicts the assumption thatunoscillates.The proof is complete.
3 Preservation of stability
Definition1 The set of all triples (a,b,c) which satisfy the condition (2) is called an asymptotical stability region denoted by H.
Followed by Definition 1,the numerical asymptotical stability region can be denoted by S.
Lemma4[18]Letφ(x)=1/x-1/(ex-1),thenφ(x) is a decreasing function andφ(-)=1,φ(0)=1/2 andφ(+)=0.
Lemma5[18]For allm>|a|,
(1+a/(m-θa))m≥eaif and only if 1/2≤θ≤1 fora>0,φ(-1)≤θ≤1 fora<0;
(1+a/(m-θa))m≤eaif and only if 0≤θ≤1/2 fora<0,0≤θ≤φ(1) fora>0,
whereφ(x)=1/x-1/(ex-1).
Lemma6 For allm>M,
(1) (1+a/(m-θa))m≥eaif and only if 1/2≤θ≤1 fora>0,φ(a/M)≤θ≤1 fora<0;
(2) (1+a/(m-θa))m≤eaif and only if 0≤θ≤1/2fora<0,0≤θ≤φ(a/M) fora>0,
whereφ(x)=1/x-1/(ex-1).
Proof(i) From (1+a/(m-θa))m≥eawe haveθ≥m/a-1/(ea/m-1).So for allm>M,in view of Lemma 4 we obtain 1/2≤θ≤1fora>0,φ(a/M)≤θ≤1fora<0.The case of (ii) can be proved in the same way.
Lemma7 Assume that inequalityp (1) 1/2≤θ≤1 or 0≤θ≤φ(1) form≥Manda>0; (2)φ(-1)≤θ≤1 or 0≤θ≤1/2 form≥Manda<0, whereφ(x)=1/x-1/(ex-1). ProofFor alla≠0,there exists aM0>0,whenm>M0,the range ofαmhas the following two cases ea≤αm Letε=min{q-ea,ea-p},ifea≤αm We will investigate which condition leads toH⊆S.For convenience,we divide the regionHinto five parts H0={(0,b,c)∈H:a=0},H1={(a,b,c)∈HH0:a>0,(a+b+c)(a+b-c)>0}, H4={(a,b,c)∈HH0:a<0,(a+b+c)(a+b-c)<0}. In the similar way,we denote S0={(0,b,c)∈S:a=0},S1={(a,b,c)∈SS0:a>0,(a+b+c)(a+b-c)>0}, S4={(a,b,c)∈SS0:a<0,(a+b+c)(a+b-c)<0}. Hi∩Hj=∅,Si∩Sj=∅,Hi∩Sj=∅,i≠j,i,j=0,1,2,3,4. Therefore,we can conclude thatH⊆Sis equivalent toHi⊆Si,i=0,1,2,3,4. Ifa>0,(2) becomes (22) (16) yields (23) Ifa<0,(2) turns into (24) (16) gives (25) Theorem6 The stability regions have the following five relationships H0⊆S0if and only if 0≤θ≤1;H1⊆S1if and only if 0≤θ≤φ(1);H2⊆S2if1/2≤θ≤1 or 0≤θ≤φ(1);H3⊆S3if and only ifφ(-1)≤θ≤1;H4⊆S4ifφ(-1)≤θ≤1 or 0≤θ≤1/2,whereφ(x)=1/x-1/(ex-1). Proof(i) Noticing that (3) and (17) are the same in form,soH0⊆S0holds for allθwith 0≤θ≤1. (ii) By the notation ofH1andS1,(22) yields (23)can be changed into Therefore,H1⊆S1if and only ifαm≤ea,so by Lemma 5 we haveH1⊆S1if and only if 0≤θ≤φ(1). (iii) By the notation ofH2andS2,(22) becomes (23) gives (iv) and (v) can be proved in the similar way. Definition2 We call the θ-methods preserve oscillation of Eq.(1) if Eq.(1) oscillates,which implies that there is anh0such that Eq.(7) oscillates forh By some easy inductions we have the next lemma. Lemma8 For allm>|a| andθ∈[0,1], (1) -a-1<-aαm/(αm-1)<-aand 00; (2) -1<-aαm/(αm-1)<0 and -a The following lemma can be naturally obtained from Theorem 2. Lemma9 Eq.(1) is oscillatory if any of the following conditions is satisfied (1)b+c<-aea/(ea-1),b≥-aandc>a/(ea-1) fora>0; (2)b+c<-aea/(ea-1),b≥0 andc>a/(ea-1) for -ln2≤a<0; (3)b+c<-aea/(ea-1),b≥0 andc>a/(ea-1),b+c>0,b<-aea/(ea-1) andc≤-afora<-ln2. By Theorem 5,Lemmas 8 and 9 the following corollary is obtained. Corollary2 For allm>|a|,under the condition of Lemma 9,if holds,then the numerical solutions inherit oscillation of the analytic solutions of Eq.(1). So we have the first result for preservation of oscillation. Theorem7 The numerical solutions inherit oscillation of the analytic solutions of Eq.(1) if one of the following conditions holds (1) 1/2≤θ≤1 fora>0; (2) 0≤θ≤1/2 fora<0. ProofFrom Corollary 2 we obtain that the numerical solutions inherit oscillation of the analytic solutions of Eq.(1) ifαm≥eafora>0 andαm≤eafora<0.Then by Lemma 5 the proof is finished. Furthermore,from Theorem 2 we can easily obtain the following lemma. Lemma10 Eq.(1) is oscillatory if any of the following conditions is satisfied (1)b+c<-a-1,b>-aea/(ea-1) andc≥1 fora>a1;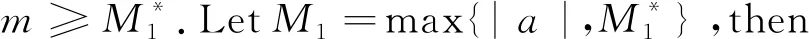

4 Preservation of oscillation
