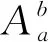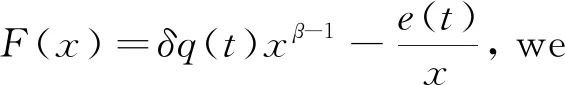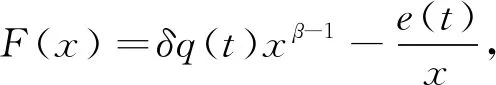Oscillatory Citerion for Nonlinear Conformable Fractional Differential Equations

WANG Peng ZHENG Zhao-wen

(School of Mathematical Sciences,Qufu Normal University,Qufu 273165,China)

Abstract In this paper,we give an oscillation criterion of interval type for second order nonlinear conformable fractional differential equations.This oscillation criterion relies on information of the coefficients on a subsequence of the positive half-line,rather than the whole positive half-line.

Key words Conformable fractional differential equation; oscillation criterion; Riccati transformation

0 Introduction

Fractional differential equations are used in various fields such as physics,mathematics,biology,biomedical sciences,finance as well as other disciplines (see [2,7]).In the last few decades,many people have been studying fractional differential equations.There are many definitions in the existent literature,such as the Riemann-Liouville,Caputo,Riesz,Riesz-Caputo,Weyl,Grunwald-Letnikov,Hadamard,and Chen derivatives.In 2004,R.Khalil et al.(see [4]) have suggested a new fractional derivative,which is called conformable derivative.This new definition has a lot of very nice properties,many properties that are consistent with the standard derivative,such as the definition itself,the chain rule that we are familiar with.In this paper,we shall investigate the oscillation criterion for the second order nonlinear conformable fractional differential equation

(p(t)y(α)(t))(α)+q(t)f(y(t))=e(t),t≥t0>0,

(1)

wherep∈C1([t0,),(0,)),q,e∈C([t0,),R),0<α≤1.

A nontrivial solution of equation (1) is called oscillatory if it has arbitrarily large zero; and otherwise it is said to be non-oscillatory.Equation (1) is said to be oscillatory if its all solutions are oscillatory.

Whenα=1,we have the following second-order differential equation

(p(t)y'(t))'+q(t)y(t)=e(t)，

(2)

Many papers involve the oscillation for equation (2) and other linear,nonlinear,damped,forced differential equations or Hamiltonian systems (see [3,8,9,10]) since the foundation work of Winter [10].

In this paper,we give a new type of oscillation criterion for equation (1),this oscillation criterion relies information of the coefficients on a sequence of interval on [t0,), rather than on the whole interval.

1 Main results

For the sake of convenience,we give some definitions and properties of conformable fractional deriva tives and integral,which are important in the proofs of the main result.We begin with the following definitions and lemmas.

Definition1 The left conformable fractional derivative starting fromt0of a functionf:[t0,)→Rof orderαwith 0<α≤1 is defined by

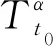
Definition2 Letα∈(0,1].The left conformable fractional integral ofαstarting att0is defined by

If the conformable fractional integral of a given function exists,we call it isα-integrable.

Lemma1 (see [1]) Ifα∈(0,1) andf∈([t0,),R),then for allt≥t0>0,we have

Lemma2 (see [4])

Lemma3 (chain rule,see [1,4,5]) Assumef,g:(a,)→Rbe (left)α-differentiable functions,where 0<α≤1. Leth(t)=f(g(t)).Thenh(t) is (left)α-differentiable and for alltwitht≠aandg(t)≠0 we have

Lemma4 (see [5]) Letf,g:[t0,t1]→Rbe two functions suchf,gisα-differentiable.Then

Lemma5 (see [6]) SupposeXandYare nonnegative.Then

λXYλ-1-Xλ≤(λ-1)Yλ,λ>1,

where equality holds if and only ifX=Y.

Fora,b∈Rsuch thata

D(a,b)={u∈C1[a,b]:u2(t)>0,t∈(a,b),u(a)=u(b)=0}.

Letρ∈C1([t0,),R) be a positive function.For givenf∈C([t0,),R)as in [11],we define an integral operatorin terms ofH∈D(a,b)andρas

(3)

(4)

(5)

wheref1,f2,f∈C([t0,),R),g∈C1([t0,),R) andα1,α2are real numbers.

(6)

fori=1,2, where

then equation (1) is oscillatory.

ProofSuppose to the contrary that there exists a nontrivial solutiony(t) of equation (1) which is not oscillatory.Without loss of generality,we may assume thaty(t)>0 on [T0,) for someT0≥t0. Set

(7)

Then differentiating (7) and making use of equation (1),it follows that for allt≥T0, we have

(8)

F(x)≥F(x*)=Qe(t)，

(9)

So (8) and (9) imply thatV(t) satisfies

(10)

(11)

Then in view of (10),(11) and the properties (3) as well as (4),we see that