一个修正的周期Camassa-Holm系统解对初值的不一致连续依赖性
2020-01-15王海权
王海权 付 英
(西北大学 数学学院、非线性科学研究中心,陕西 西安 710127)
0 引言
本文考虑周期情形下一个修正的Camassa-Holm系统初值问题,具体如
(1)
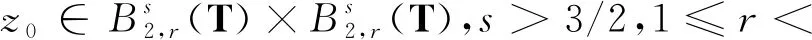
符号说明 若A≥cB或者A≤cB,其中c是仅与指标有关的正常数,每一行的取值不尽相同.若z=(u,ρ)则‖z‖X×Y=‖u‖X+‖ρ‖Y,其中X和Y是Banach空间.
1 预备知识
为了估算方便,将问题 (1) 化为如下形式
(2)
接下来,给出Besov空间的定义和性质.
定义1[12,13]设s∈R,1≤p,r≤. 非齐次的Besov空间定义为
命题1[12,13]设s∈R,1≤p,r,pi,ri≤(i=1,2) 则有
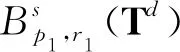
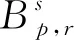
(f) 令m∈R,f是一个Sm乘子,则对任意的s∈R,1≤p,r≤,f(D)是从到的连续算子.
对于输运方程的初值问题
(3)
有以下结论.
引理1[14]令(p,r)∈[1,]2,s>-d/p,v是一个向量场,使得否则假设若u∈L是问题(3)的解,则当r=1或者s≠1+d/p则

若u∈L是问题(3)的解,则当s>0时,
成立.然后给出一些重要的不等式.
引理3[9]令σ,α∈R.若n∈Z+,则对于任意的1≤p,r≤有
引理4[12]假设(p,r)∈[1,]2,则有
(2) 对于s1≤1/p,s2>1/p(s2≥1/p,r=1)以及s1+s2>0,

(4)

2 定理1的证明
在这一部分,通过构造近似解[7-11]的方法来证明定理1.
2.1 近似解估计
首先,构造如下近似解
uω,n(t)=ωn-1+n-scos(nx-ωt),γω,n(t)=ωn-1+n-scos(nx-ωt),
其中ω=±1,n∈Z+,s>3/2.将上面构造的近似解代入问题(2)的方程,可设
≤cnμ-2s+1+cnμ-2s-1+cnμ-s-2≤cnμ-2s+1+cnμ-s-2.
引理6若ω=±1,n∈Z+,1/2<μ<1,s>3/2,1≤r<则
2.2 近似解与解的差的估计
设(uω,n(t),γω,n(t))是如下问题的解,即满足
(5)
由引理3可知
所以根据引理5知 (uω,n(t),γω,n(t))是问题(5)的唯一解,并且解的最大存在时间
为了估算近似解与解的差,设σ=uω,n-uω,n,η=γω,n-γω,n将其代入(5),则有
(6)
其中
对问题(6)的第一个方程和第二个方程分别使用引理1可得
根据命题1,对于1/2<μ 由引理4可得 根据引理3以及引理5可知 于是有 引理7若ω=±1,n∈Z+,1/2<μ 根据引理3以及引理5可知 因此可知z1,n(t)和z-1,n(t)是问题(5)初值分别为z1,n(0)和z-1.n(0)相对应的解,并且解的最大存在时间T0与n无关.取定n且足够大,设k=2s-μ,对问题(5)的两个方程使用引理2得 利用命题1(b)以及引理4分别估算上述两式每一项可得 将上面两式相加,然后利用引理5以及Gronwall不等式可得 进一步有 结合命题1(e)以及引理7可得 再结合引理3,引理5以及uω,n和ρω,n的定义有 最终,对于任意的0≤t≤T有 通过引理3然后两边同时取极限可得 定理1证毕.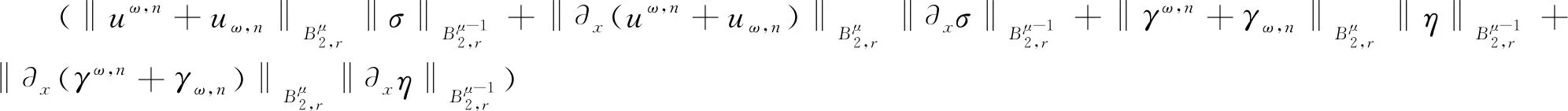

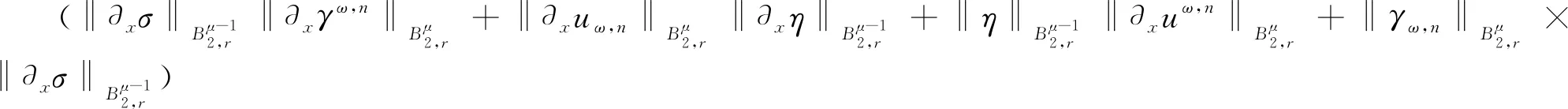
2.3 完成定理1的证明
