基于闪电搜索算法的水泵流量-扬程样本曲线校准
2020-01-14王津生
丁 祥, 王津生, 李 剑, 王 彤, 赵 明
(1.长安大学 基建处,陕西 西安 710064;2.河北建设投资集团有限责任公司,河北 石家庄050051;3.长安大学 建筑工程学院,陕西 西安 710061;4.哈尔滨工业大学 市政环境工程学院,黑龙江 哈尔滨 150090;5.天津三博水科技有限公司,天津 300070)
在城市配水系统中,泵站是最大的耗电单元,其用电量约占总用电量的95% ~98%,其余2% ~5%用在供水过程中的辅助设备上(例如电动阀、排泥机、风机及照明等)[1-3]。泵站的节能降耗具有重要意义,而泵站的优化调度必须具备符合实际的水泵特性曲线。随着水泵的老化,水泵样本特性曲线已经不能准确地反映其性能,需要重新描述。
实际生产中,水泵的特性曲线常通过实测获得,但是这种方法存在很多弊端:需要在各水泵的压水管路上安装压力计和流量计,增加了生产成本;实测期间压力和流量变化较大,容易发生爆管或导致供水不足,影响水厂的安全生产。笔者采用闪电搜索算法基于MATLAB平台进行编程,求解水泵流量-扬程曲线的参数,并提出了一种利用水泵开启组合和出厂流量、压力数据来校准样本曲线的方法,以期为泵站生产运行和节能降耗提供基础。
1 数学模型的建立
1.1 数解法求水泵装置的工况点[4]
水泵的装置工况点数解,其原理是通过联合水泵特性曲线和管道系统特性曲线方程求解Q和H。即:

式中,H为泵的扬程,m;Hx为泵在Q=0时所产生的虚总扬程,m;Sx为泵内的虚阻耗系数;S为管道的虚阻耗系数;m为指数,给水管道一般取2或1.84。
联立式(1)和式(2),可得:
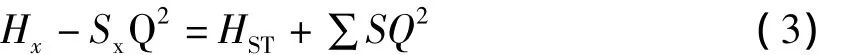
化简可得水泵的流量,即:

1.2 数解法求调速泵曲线[3]
设转速为n1时,泵(Q-H)1曲线方程为H1=Hx-SxQ21;转速为n2时,泵(Q-H)2曲线方程为H2=H x'-S'xQ22。在(Q-H)1曲线上取两个点(QA,HA)和(QB,HB),相应的在(Q-H)2曲线上取两点(Q'A,H'A)和(Q'B,H'B)。则:
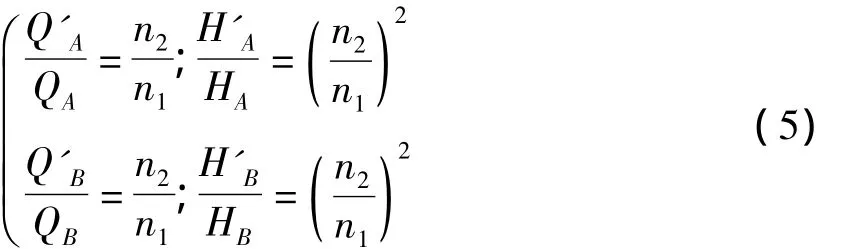
把式(1)代入(Q-H)1曲线表达式中,可得:

同理,当转速为n2时,(Q-H)2曲线方程中的参数:

联立式(1)和式(3)得到:
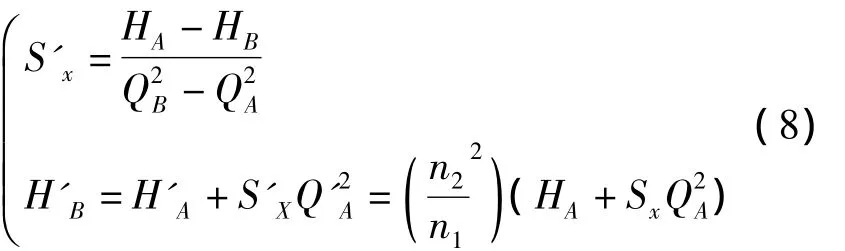
综合式(2)和式(4)得到:
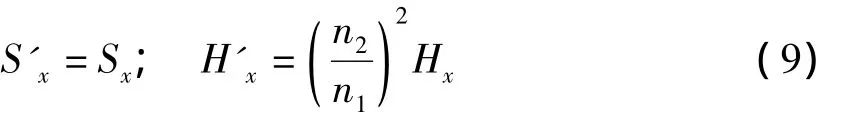
则(Q-H)2曲线表达式:
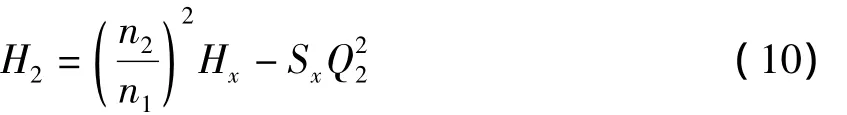
1.3 数解法求调速运行下的并联工况[3]
供水区域内用水量的增减会导致泵站出厂流量和压力变化,为保证用户的用水需求,泵站可采用调速运行的方式来实现均匀供水。
假设某水厂的二级泵站有2台不同型号的水泵并联工作,如图1所示。

图1 调速泵站Fig.1 Speed regulating pump station
1#泵为定速泵,其(Q-H)曲线的方程:

2#泵为调速泵,转速为 n1时,其(Q-H)曲线方程:

节点3的总水头:

则水泵的出口压力:

联立式(4)、(13)和(14)计算定速泵流量:

转速为n2时,由式(10)计算调速泵的曲线:H,由式(4)可得到调速泵的出口流量:
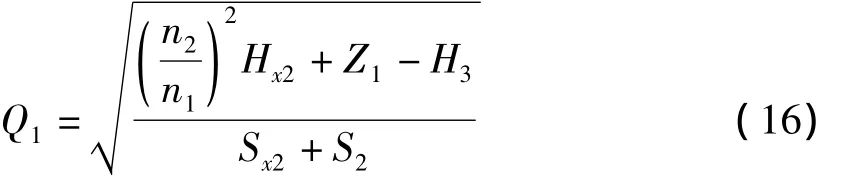
水厂的目标供水量为QT,按照连续性方程,需满足 Q1+Q2=QT,即:

1.4 目标函数的建立
根据式(17)建立曲线校准的数学模型:
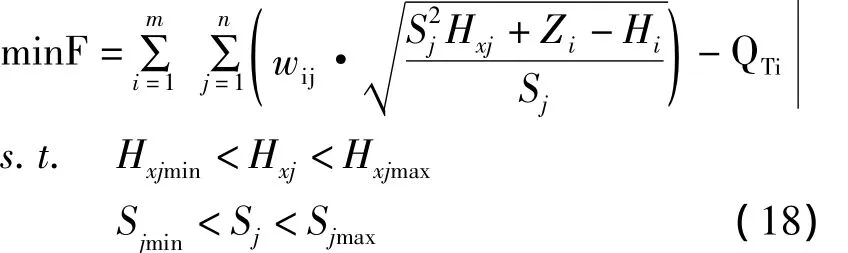
式中,m为水泵开启组合个数;n为水泵总台数;wi,j为第 i种泵开启组合中第 j台泵的开停状态,1为开启,0为关闭;Sj为第j台水泵的调速比;Hxj为第j台水泵的虚总扬程,m;Sxj为第j台水泵的虚阻耗系数;Zi为第i种开泵组合的吸水池水位,m;Hi为第i种开泵组合的泵站出口压力,m;QTi为第i种开泵组合的出厂流量,m3/h;Hxjmin和Hxjmax分别为第j台水泵虚总扬程的最小值和最大值,m;Sjmin和Sjmax分别为第j台水泵的调速比的最小值和最大值。
2 闪电搜索算法
2.1 概述
2015年,Hussain Shareef等基于闪电的机理提出了一种新型的启发式优化算法——闪电搜索算法(lightning search algorithm,LSA)[5],该算法具有调节参数少、收敛精度高和全局寻优能力强等优点,已在函数优化、旅行商问题寻优等方面得到应用[6]。
2.2 LSA的基本原理
LSA主要通过3种放电体的数学模型模拟来实现,即过渡放电体、试图成为领先者的空间放电体、源于过渡放电体群并代表最佳位置的引导放电体。
2.2.1 过渡放电体
初期就形成了一个先导放电体,经过过渡形成了一个随机方向的放电体。因此,可以认为它是从解空间的开区间上的标准均匀概率分布中取得的一个随机数。设一个群体规模为N的梯级先导sl=[sl1,sl2,…,slN],其满足待优化问题的 N 个随机放电体位置PT=[PT1,PT2,…,PTN]。标准均匀分布的概率密度函数f(xT)可以表示为:

式中,xT为可提供候选解或梯级先导sli的初始顶端能量Esli的随机数;a、b分别为解空间下限和上限。
2.2.2 空间放电体
一旦这N个先导放电体进化完成,需要电离上一代先导放电体才能形成下一个通道。设空间放电体的位置为 PS=[PS1,PS2,…,PSN],利用指数分布函数随机生成数进行数学建模。其指数分布概率密度函数f(xS):
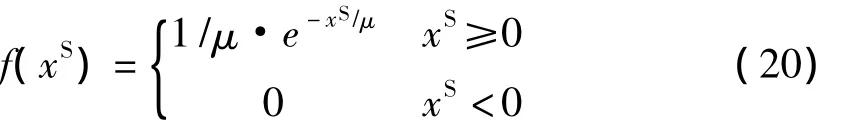
空间放电体的位置或下一次迭代的方向可以通过形状参数μ来控制。在LSA中,μi为引导放电体PL和空间放电体之间的距离。依据这一定义在第t+1次迭代位置可以描述为:

其中,erand是指数随机数。如果PSi为负,那么产生的随机数应该被减去,因为式(20)只提供正值。然而,新位置PSi_new不能保证梯级先导传播或通道的形成,除非空间放电体能量ESp_i大于先导放电体能量Esli或者找到一个更好的解。如果在下一步提供了更好的解,那么相应的先导放电体sli被扩展到新位置 sli_new,并且被更新到。否则,保持不变,直到下一次迭代。如果延伸到并优于当前迭代,则空间放电体将变成引导放电体。
2.2.3 引导放电体
利用具有形状参数μ和尺度参数σ的标准正态分布生成的随机数进行数学建模,其正态概率密度函数f(xL)表示为:
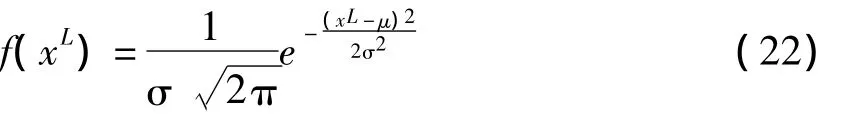
由式(20)可知,随机生成的引导放电体可以从形状参数所定义的当前位置的所有方向上进行搜索,并且可通过尺度参数定义其开采能力。在LSA中,引导放电体PL的尺度参数σ随着向地球的推进或找到最佳解而呈指数下降。有了这个定义,引导放电PL在第t+1次迭代位置可以描述为:
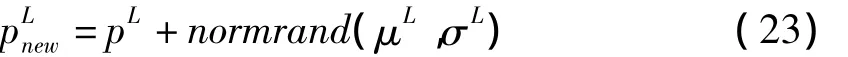
LSA的整个过程总结为图2所示的流程。
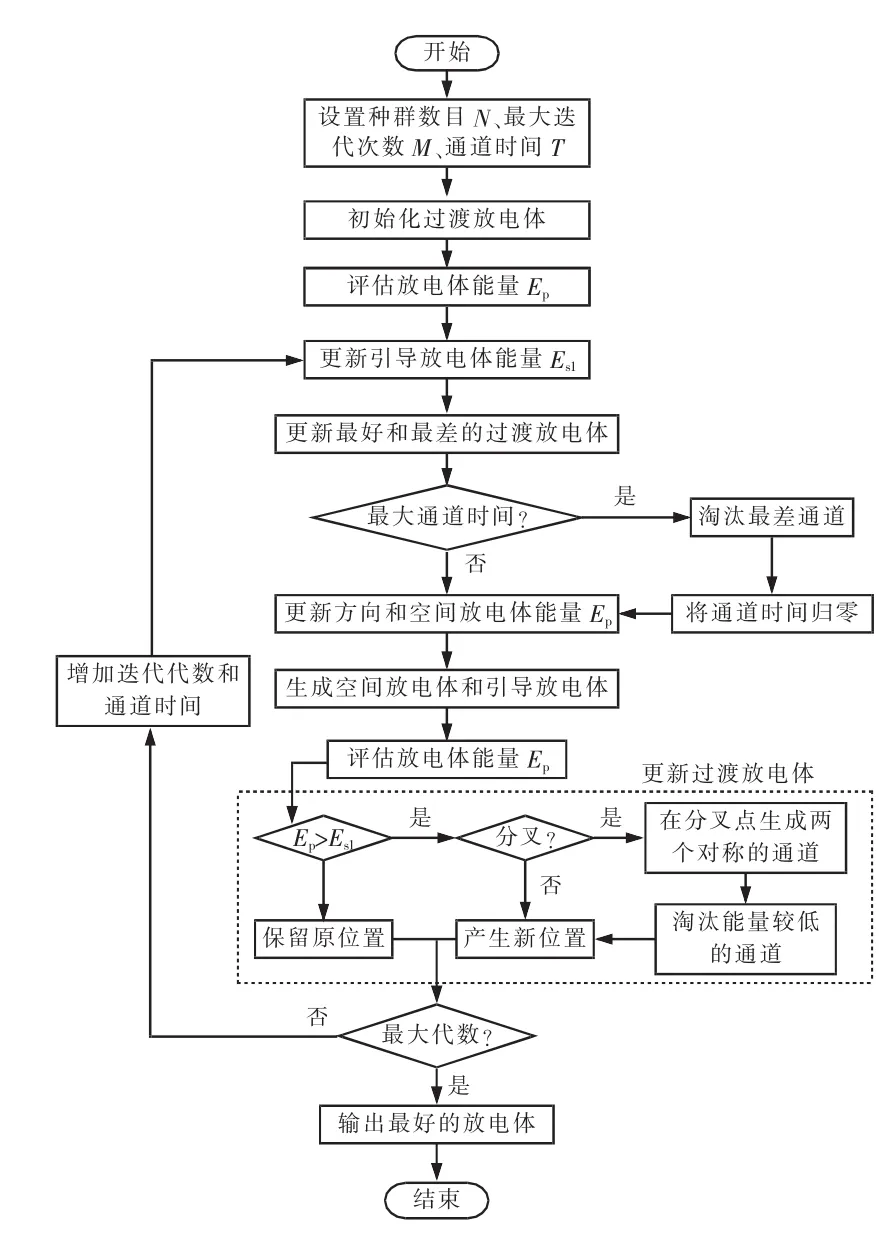
图2 LSA的流程Fig.2 Flow chart of LSA
3 工程实例
3.1 泵站基础数据
T市某水厂的二级泵站设计水量为50×104m3/d,目前共安装水泵9台。2017年7月20日的水泵组合和调频数据中,其中有14种水泵开启组合如表1所示。
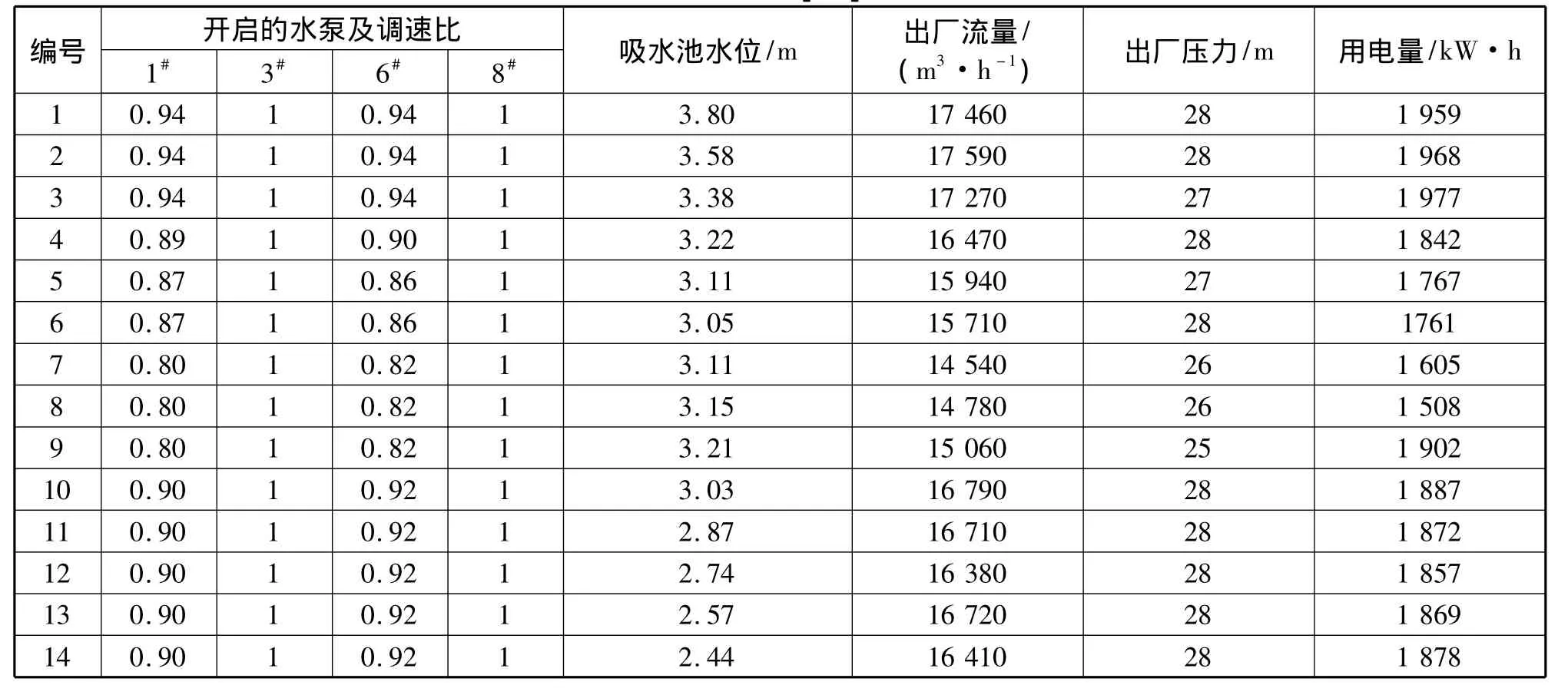
表1 水厂水泵组合Tab.1 Combinations of pumps in waterworks
3.2 数学模型的优化
从表1可知,收集的泵站出口压力数据仅保留到整数位,若按照数学模型进行计算,会产生很大的误差。因此,需要将出厂压力H加入到变量中。根据四舍五入的原理,H的取值范围为[H-0.5,H+0.5],得到经过改良的数学模型:
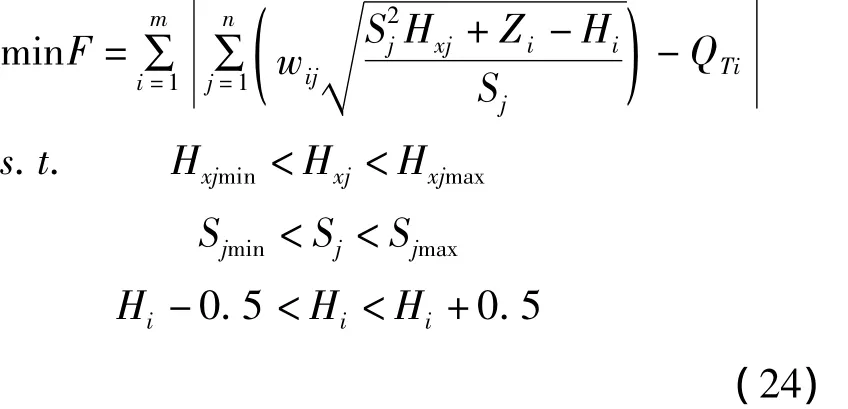
式中,Hi为第i种开泵组合的泵站出口压力,m。
3.3 模型的求解
根据已有的样本曲线,拟合出各型号水泵相应的Q-H曲线见表2。

表2 部分水泵Q-H样本曲线Tab.2 Q -H sample curves of some pumps
闪电搜索算法的参数设置:未知数23个,种群个体50个,最大迭代次数2000,最大通道时间为10。增加一个循环终止条件,即最差个体等于最优个体。
水泵使用后,Hx参数的变化不大,取0.97~1.03倍的样本曲线值;管道摩阻Sx参数会显著增大,取样本曲线值的0.9 ~1.4 倍。1,3,6,8 号泵的 Hx取值范围为:51.9·[0.97,1.03],53.53·[0.97,1.03],53.53·[0.97,1.03],43.41·[0.97,1.03];Sx的取值范围为:- 6.425e - 7·[0.9,1.4],-1.271e -6·[0.9,1.4],- 1.271e - 6·[0.9,1.4],-4.426e-7·[0.9,1.4];水泵出口压力取[H -0.5,H+0.5]。
经过运算,迭代760代后算法终止,在435代时收敛到最小值 2475.1671,得到最优解空间为[50.344,51.968,51.944,42.109,8.768e - 07,1.769e- 06,1.774e - 06,6.196e - 07,24.658,24.349,24.120,24.807,24.390,25.158,23.390,23.350,22.290,24.745,24.940,25.664,24.930,25.603]。相应的适应度函数如图3所示。
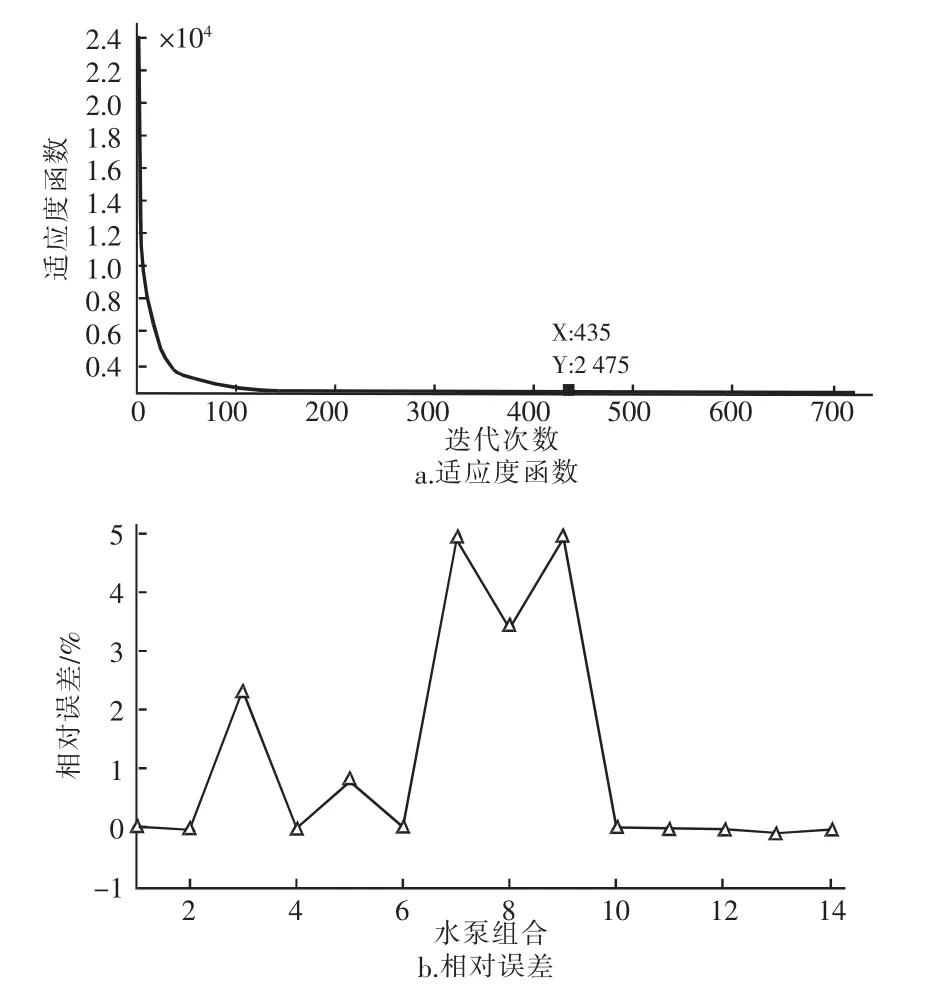
图3 程序运行结果Fig.3 Result diagram of program running
由图3.a可知,LSA的全局搜素能力很好,在150代的时候适应度函数值就降到2520,最终在435代时降到2475.1671。由图3.b可知14个流量的相对误差全部控制在5%以内,平均相对误差为1.171%。其中有9组模拟值误差为0,2组在0~3%之间,3组在3%~5%之间。因为该水厂日报表数据均为人工记录,可认为第7~9组数据存在人为失误。因此,该精度满足要求,即模拟出的水泵曲线是可信的。
在各水泵的高效段内分别绘制出样本曲线和模拟曲线,其对比情况如图4所示。
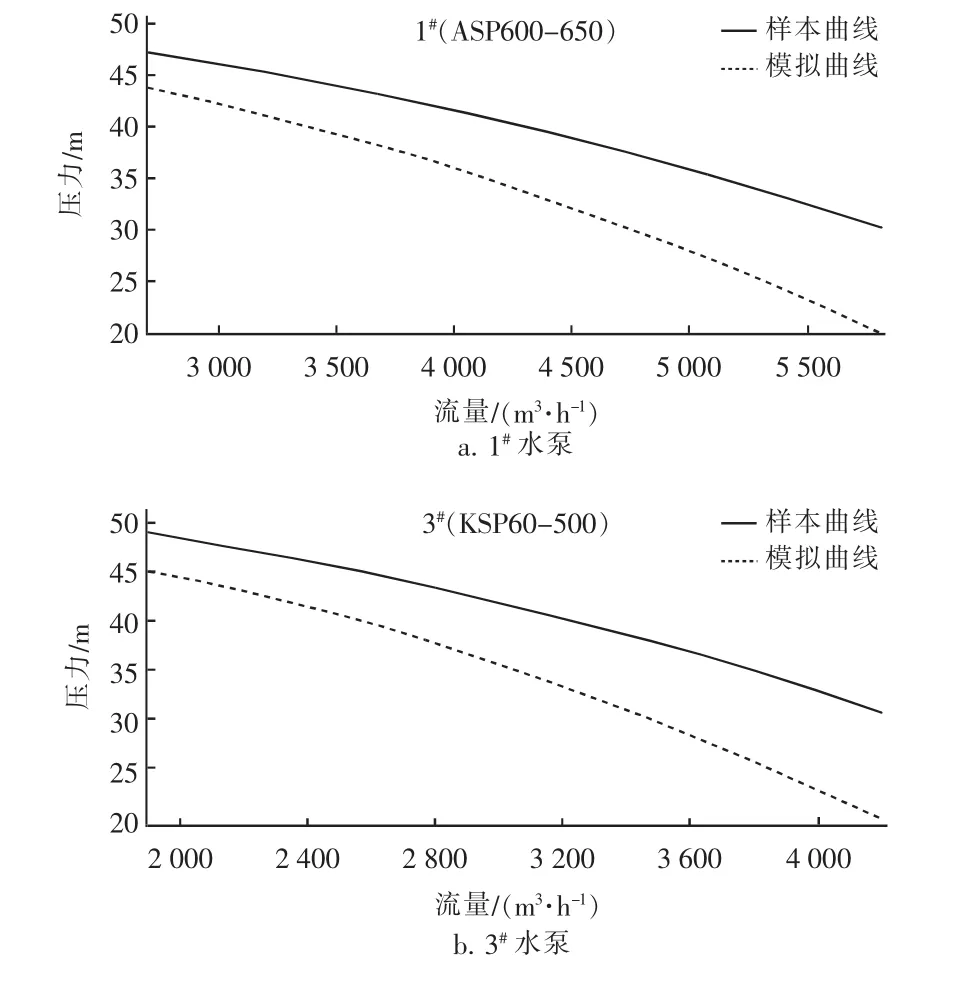
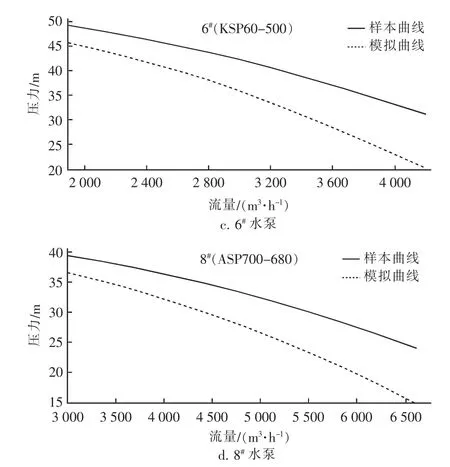
图4 样本曲线和模拟曲线的对比Fig.4 Comparison of sample and analog curves
水泵长期使用,老化比较严重,会使样本曲线与模拟曲线产生相应的差距,最终各水泵的Q-H曲线见表3。
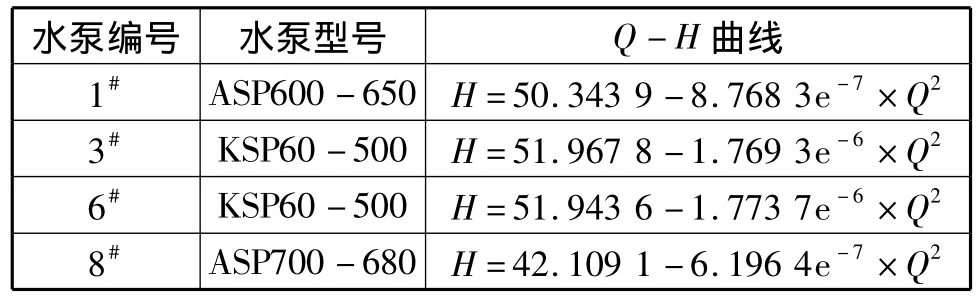
表3 部分水泵Q-H模拟曲线Tab.3 Q - H simulation curves of pump
4 结论
① 建立了一个23维非线性的目标函数,采用了闪电搜索算法对其进行求解。该算法非常快速地收敛到了全局最优解,展现出了非常优秀的全局搜索能力,可以很好地解决复杂的寻优问题。
② 新的水泵流量-扬程曲线校准方法先拟合水泵的理论曲线,然后用泵站的组合数据和出厂流量、压力数据来校准样本曲线。该方法不需要在水泵压水管上安装仪表,节约成本,并且不影响水厂的正常供水。
