抗差卡尔曼滤波在危房监测中的应用
2020-01-14杨振乾
杨振乾
(重庆市勘测院,重庆 401121)
1 引 言
随着城镇化速度的不断加快,城市内土地的过度利用,大量的建筑出现。但危房不能短时间内全部拆除,需利用专用的测量仪器对房屋的沉降、裂缝、应力和倾斜等进行专业化的监测及预报[1,2]。在危房监测过程中,由于各种主观和客观因素的影响,监测数据中可能混入粗差,影响监测数据的可靠性,如果不能及时剔除粗差,对数据处理的结果造成严重的影响。因此对危房进行有效的监测,并对监测的数据进行有效的处理十分重要,它对于我们是否能够及时发现房屋危险状况并进行及时地处理有十分重要的意义。
目前,在测量领域中经常运用卡尔曼滤波模型对动态监测数据进行处理[3],包括高铁网的监测[4]、地震预测[5]和建筑物的监测等,证明其可通过剔除随机干扰噪声,是一种十分有效的数据处理方法。建筑物变形一般由以下两个因素造成的:地基的深度,若地基的应力超过其承载力,则会导致建筑物不规则下沉,进而导致建筑物倾斜或者塌陷;时间,随着时间的推移,建筑物会朝某个方向缓慢地移动。根据建筑物的变形原因和变形特征,建筑物的测量噪声为白噪声,符合高斯分布的特征;由于建筑物的变形随着时间的推移朝着一个方向进行变化,其符合线性特征;t时刻的变形量可以依据t-1时刻状态推出,与0~(t-2)时刻无关,故符合贝叶斯滤波的马尔可夫假设。因此可以在建筑物监测中应用卡尔曼滤波模型。
当建筑物观测值中含有粗差时,卡尔曼滤波不能对其进行有效的探测和消除,从而导致利用卡尔曼滤波对含有粗差的监测数据进行处理得到的结果会出现较大的偏差,进而导致数据处理结果发生扭曲,会造成严重的后果。因此在测量界一直在寻找一种可以有效抵抗粗差的数据处理方法,直到近些年来,很多学者将抗差估计引入测量界,将抗差估计融入卡尔曼滤波模型中,证明了其可以有效抵抗粗差的影响[6]。本文以标准卡尔曼滤波为基础,以危房监测为研究对象,建立抗差卡尔曼滤波模型并将其应用于工程实践中。
2 抗差卡尔曼滤波模型
2.1 抗差估计
近些年来,学者们相继提出了很多抗差估计方法,我们一般将其归纳为3类:极大似然型估计(M估计)、非参数型秩检验估计(R估计)和顺序统计量线性组合型估计(L估计),其中比较常用的是M估计。下面主要介绍M估计[7]:
假设有一组分布密度为f(vi)的观测值样本L1,L2,…,Ln,对于M估计的估值需要满足以下条件:
(1)
令ρ(·)替换-lnf(·),V=BX-L,则:
(2)
式(2)为基于独立等精度观测的准则,如对于独立不等精度观测的情况,则:
(3)
抗差M估计的抗差性主要由使用的函数所决定,而函数的选取又与观测数据的结构有关,函数又决定了权函数,常见的权函数如表1所示:
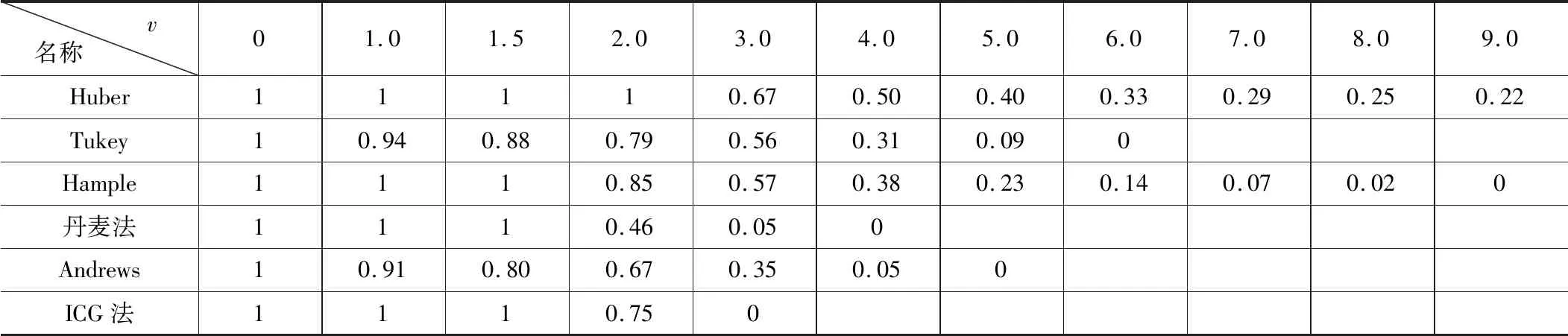
权因子w变化表 表1
通过权因子变化表和大量的实验证明,ICG法对大误差更具有抵制能力;对于小误差来说Tukey法和Andrews法较有效,Huber法对实际重尾分布具有较好的效率。每种权函数有各自的适用情况,合理选择权函数对抗差估计至关重要[8]。
2.2 模型建立
由于抗差估计具有抵抗粗差的能力,因此我们将卡尔曼滤波模型的滤波特性与抗差估计理论的抗差性相结合,对外业采集的观测数据进行数据处理使其在观测值有粗差的情况依然可以得到精度较高的估计值。抗差卡尔曼滤波模型的主要特点是:以抗差估计为基础来对标准卡尔曼滤波进行改进,通过分析增益矩阵来选取合适的权函数,然后用其替换观测噪声协方差阵;选定权函数后,利用广义最小二乘原理可推导出抗差卡尔曼滤波的递推方程[9]:
状态预报
(4)
状态协方差阵预报
(5)
滤波增益矩阵
(6)
状态估计
(7)
状态协方差阵估计
(8)
(1)先根据观测噪声的原始权阵求出递推方程的参数估值、观测值的残差和单位权方差;
(2)根据第(1)步计算的观测值残差和单位权方差确定各观测噪声的权因子然后计算相应的等价权;
(3)然后按照上述抗差卡尔曼滤波计算公式计算出参数估值,各观测值的残差和单位权方差;
(4)若前后两步的参数估值小于指定限差,则停止计算,否则返回第(2)步重新计算。
抗差卡尔曼滤波的计算流程图如图1所示。
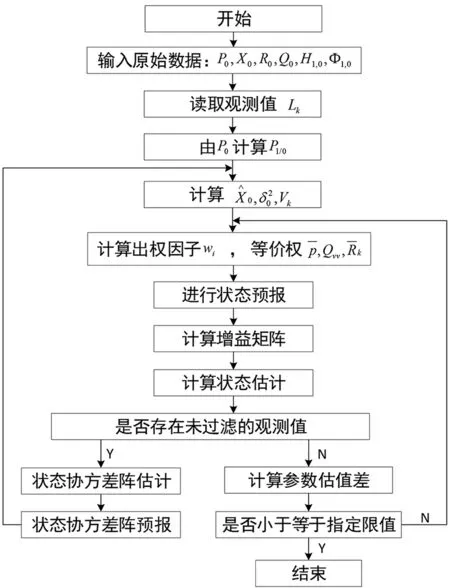
图1 抗差卡尔曼滤波计算流程
3 工程应用
3.1 数据采集
本次监测采用GNSS定位监测技术,以此建立危房监测数据采集平台,本次实验是对贵州省某区域的危房进行连续14天的变形监测。本次实验主要设立1个基准点和5个监测点,监测点和基准点相对位置的网形示意图如图2所示。
本次GNSS监测网中的监测点均布设在同一幢楼房的房顶,楼房为砖混结构,约 30 m高,基准点设置在离楼房约 4 km的空旷地,仰角10°以上无遮挡,监测站均采用NOVTEL OEM6板卡接收机和自主研制的天线,可同时接收GPS和BDS数据。本次基准点命名为BASE,5个监测点分别命名为BP1,BP2,BP3,BP4和BP5,监测点间的距离大约 20 m。本次实验数据采集时间段为2016年8月6日~2016年8月19日(共14天),全天候24小时连续观测,采样间隔为5秒,每天可观测 17 280个历元。
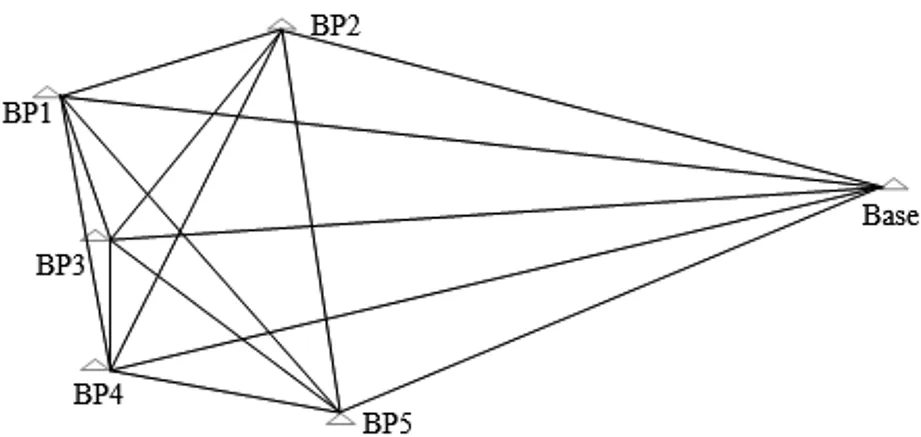
图2 监测点和基准点网形示意图
3.2 数据采集
本此实验对采集的GNSS数据进行双差载波相位解,消除接收机钟差、卫星钟差,由于本次的GNSS测量网的基线较短,所以对流层和电离层的影响对定位结果影响较小。本次使用Gamit软件对GNSS数据进行基线解,为了获取高精度的解,本次将GPS与BDS进行融合求解基线解,本次计算GNSS数据1小时的解,共获得336期监测数据,然后通过科傻平差软件求出坐标平差解,并将其投影在平面上,获得5个监测点的平面坐标位置和高程坐标值。
接下来利用卡尔曼滤波模型和抗差卡尔曼滤波模型对平差后的数据进行数据处理分析。由于监测对象的动态性不强,变形趋势缓慢,故将监测点位置和变形速率作为状态参数,则单一测点的滤波方程为:
(9)
(10)
由于建筑物的变形量比较小,监测数据的粗差比较小,故需要选择对粗差敏感性比较强的权函数,本次抗差卡尔曼滤波处理中利用Tukey法求取M估计的权函数,进而得到模型的权因子,通过平差的方法求得模型的初值,根据观测量的数据处理方法确定观测噪声的方差阵,再确定动态噪声的方差阵。然后通过抗差卡尔曼滤波模型和标准卡尔曼滤波模型对监测数据进行数据处理,得到各个监测点的抗差卡尔曼滤波模型滤波值、标准卡尔曼滤波模型滤波值。监测点BP4的观测序列如图3、图5、图7,由于危房变形是缓慢的,观测期间外界环境条件是稳定的,通过观测序列可看出本次监测数据中存在数据突变的情况;利用粗差探测方法,通过计算发现观测值中含有真误差大于三倍中误差的情况,由此推测危房监测数据中存在粗差。分别利用标准卡尔曼滤波和抗差卡尔曼滤波模型对其进行处理得到滤波结果如图3~图8所示(其他监测点类似):
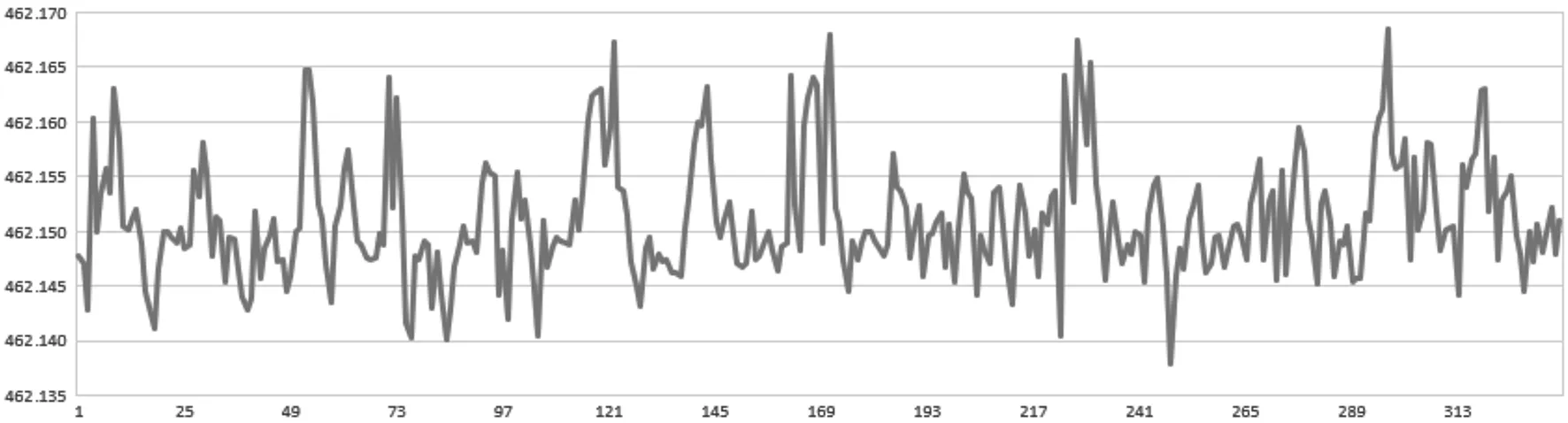
图3 监测点BP4 x方向观测序列
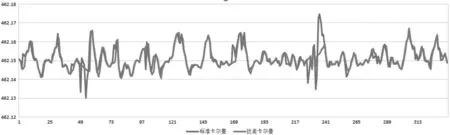
图4 监测点BP4 x方向标准与抗差卡尔曼滤波值
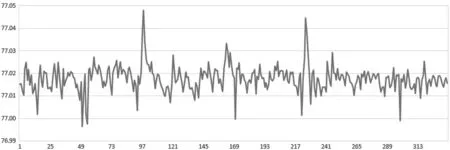
图5 监测点BP4 y方向观测序列
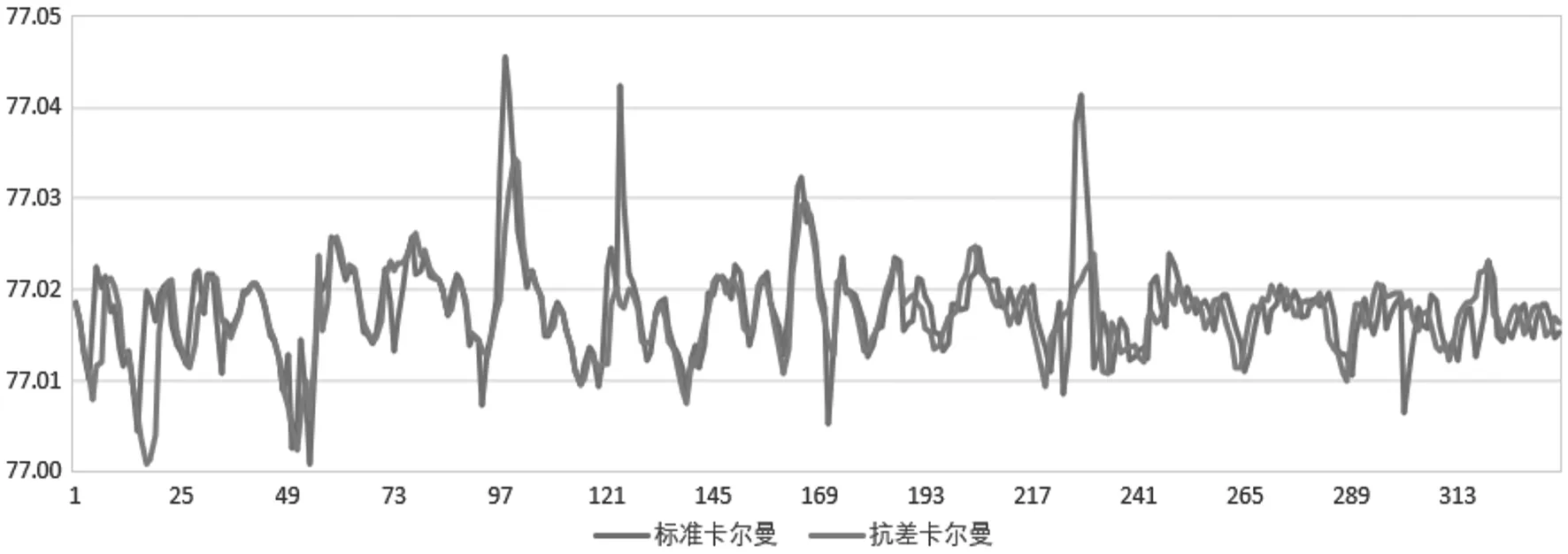
图6 监测点BP4 y方向标准与抗差卡尔曼滤波值
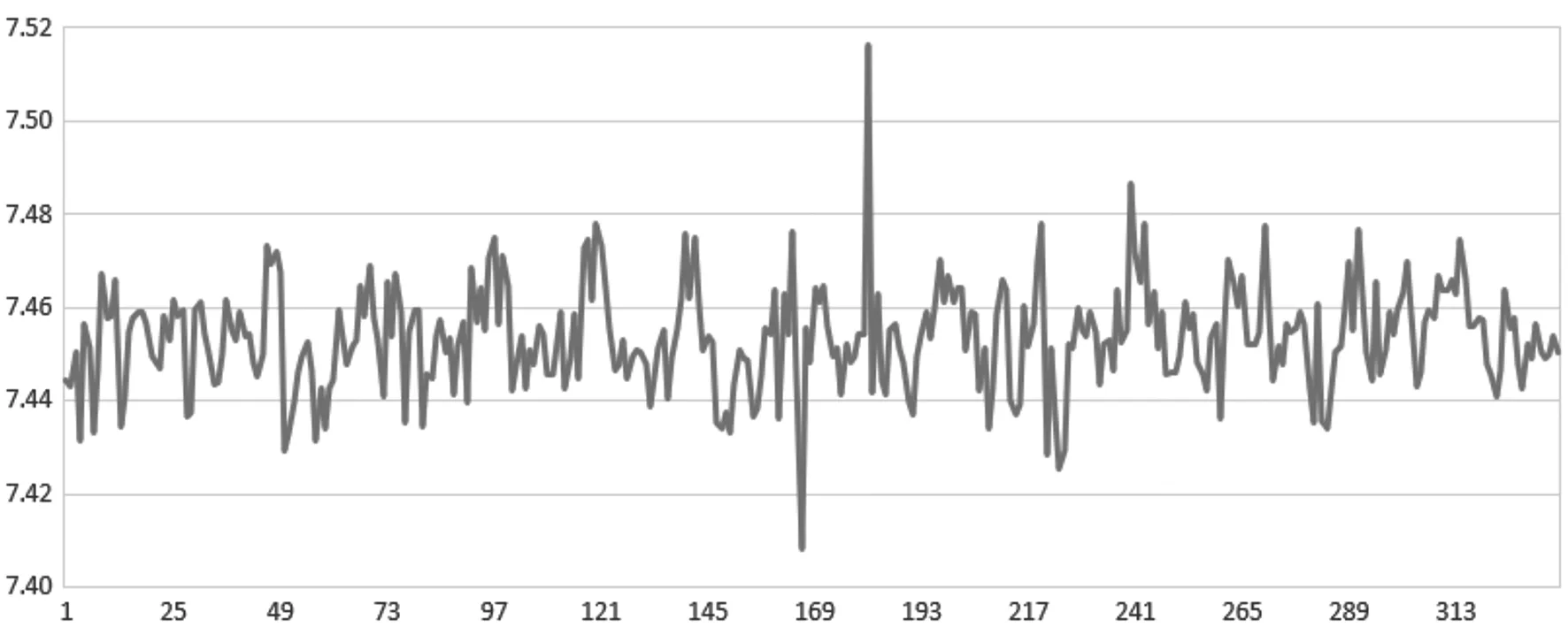
图7 监测点BP4 H方向观测序列
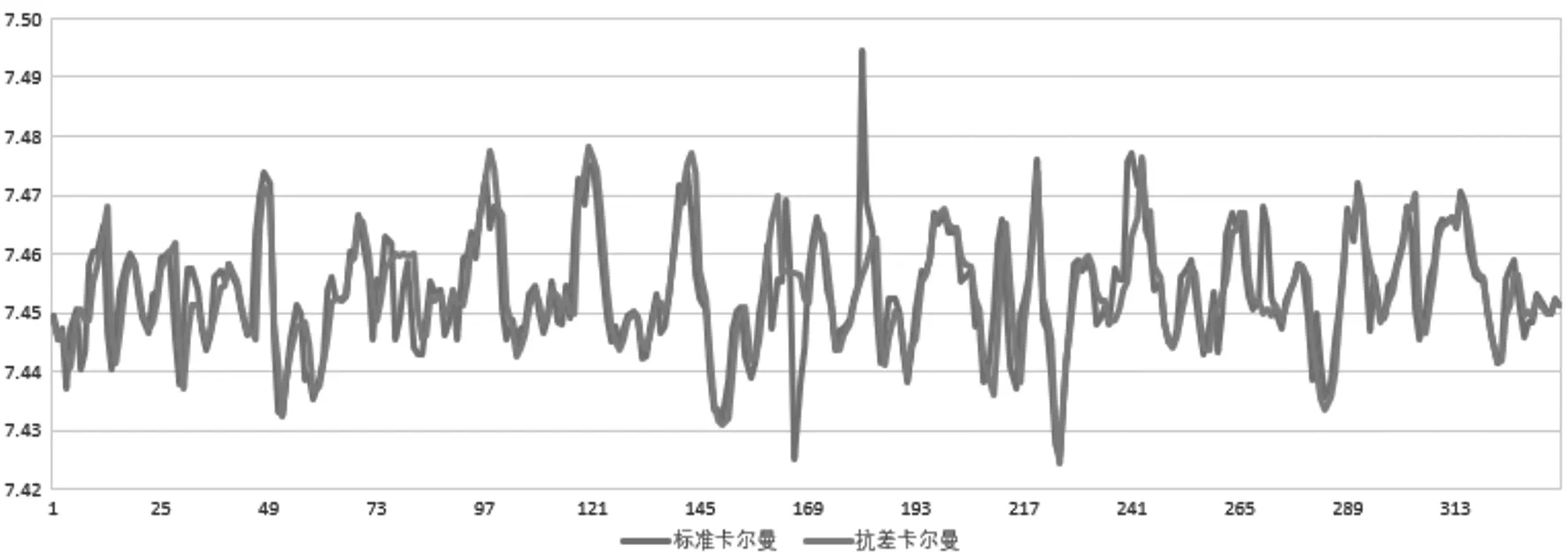
图8 监测点BP4 H方向标准与抗差卡尔曼滤波值
从图3~图8我们可以分析得到以下结论:
(1)通过平差结果和滤波结果,通过滤波处理能提高GNSS监测系统的精度;
(2)通过平差结果和滤波结果,滤波可以过滤观测序列的部分噪声,使得滤波后的监测数据更加平缓,更加符合建筑物的变形特征;
(3)本次选取的权函数能够有效地应对本次监测数据中出现的粗差;
(4)通过对标准卡尔曼滤波和抗差卡尔曼滤波的结果进行比较,观察到抗差卡尔曼滤波的波形较稳定,能够有效地削弱或消除粗差的影响,证明抗差卡尔曼滤波模型能够有效抵抗粗差的影响。
4 结 论
本文将抗差估计与卡尔曼滤波相结合建立抗差卡尔曼滤波模型,利用其对某地的危房监测数据进行数据处理,其结果表明其可以有效地处理危房监测数据,在危房监测方面具有较好的应用前景。
