基于NES-双管隔振器耦合系统的动力学分析

李世霖

(中国民航大学 航空工程学院,天津 300300)

阻尼器广泛存在于土木工程、航空航天工程和汽车工程等不同领域。NARKHEDE等[1]研究了非线性流体黏滞阻尼器在半周期正弦冲击激励下的瞬态响应，并进一步研究了非线性阻尼和附加阻尼对系统的影响。郑璐等[2]综述了三种非线性黏性阻尼器的研究进展，即非线性能量汇(NES)、粒子冲击阻尼器(PID)和非线性黏滞阻尼器(PTC),并对非线性刚度和非线性阻尼进行了分类。方智伟等[3]研究了非线性能量汇(NES)与超磁致伸缩材料(GMM)相耦合的新模型，并对系统进行了振动控制和能量采集。徐兆东等[4]研究了一种阻尼性能更好的小变形、高承载的冲击减振装置，并对物料和空气弹簧进行了考虑和建模。为了实现在航空航天工程中的应用，戴宏华等[5]建立了精确的生物激励分离模型，分析了在地面和空间环境中的减振性能。PEPE等[6]提出了一种变分反馈控制器，并将其应用于半主动激波中，证明了其在突变处理上的优良性能。张玉新等[7]研究了一种S型双腔振幅敏感阻尼器，通过提供连续的阻尼力，系统可以平稳地在低阻尼和高阻尼之间切换，为车辆的乘坐舒适性和行车安全性能提供了优化设计。此外，NIE等[8]研制了一种与速度相关的阻尼器，可以获得半主动阻尼器的动态性能，而且结构更加简单紧凑。

采用谐波平衡-弧长延拓法对NES-双管隔振器耦合系统进行相关分析。先建立一体化耦合系统的非线性振动方程[3,9-10]，运用谐波平衡-弧长延拓法研究系统在基础简谐激励下的稳态响应。通过研究耦合系统和NES系统位移幅频响应的最值，结果表明耦合系统具有更好的减振性能。对比分析系统参数对时域和功率的影响，揭示各参数对耦合系统的动态响应，并进一步通过系统的能量传递关系，验证一体化耦合系统在能量吸收方面的优良性能。

1 系统模型

系统工作原理如图1所示[9]，双管隔振器产生阻尼力的油液存在于三个不同的油室，即储油室、增压室和回弹室。两个进出油液的阀门分别安装在活塞和静态阀座上，分别称作压缩阀和回弹阀。在压缩行程中，增压室的压力增大，然后打开压缩阀和压缩基阀，增压室体积减小，在油液流经压缩阀和孔口时产生阻尼力。在油液流过压缩阀和节流口时，开启进气阀和压缩基阀，增压室体积减小，产生压缩阻尼力。相似地在回弹行程中，回弹室的液压升高，而负压发生在增压室。因此，回弹室和储油室中的油，通过两个回弹阀和回弹孔流入增压室，产生回弹阻尼力。

图1 工作原理

如图2给出了NES-双管隔振器耦合系统连接在一个线性主系统上的力学模型。由牛顿第二定律列出如下非线性控制方程[3]

(1)

其中:m1,k1和c1分别为单自由度卫星系统的质量、刚度和阻尼；m2,k2和c2分别为NES的质量、非线性刚度和阻尼；x1为单自由度卫星系统的位移，x2为NES系统的位移；FD为双管隔振器提供的等效阻尼力[9]，cd为油液的等效阻尼。在发射阶段卫星所受到的位移激励x0作用在基座上，可以表示为：

x0(t)=Asin(2πfi)

(2)

其中A为基础位移幅值，f是激励频率。

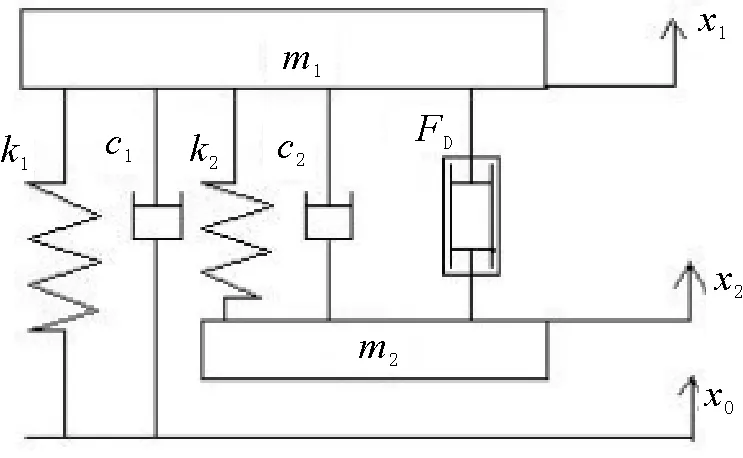
图2 系统模型

2 对比分析

由于整星隔振系统是强非线性激励系统,通过谐波平衡法对方程(1)进行近似求解,假设方程(1)的谐波解满足如下形式：

x1(t)=a11cos(ωt)+b11sin(ωt)+a31cos(3ωt)+b31sin(3ωt)x2(t)=a12cos(ωt)+b12sin(ωt)+a32cos(3ωt)+b32sin(3ωt)

(3)

其中a和b表示一阶、三阶傅里叶系数(i=1,3;j=1,2)。将方程(2) (3)代入方程(1)，借助mathematica的符号推导功能，对代数方程组进行推导和简化得到cos(ωt),sin(ωt),cos(3ωt)和sin(3ωt)系数分别相等的8个代数方程式。在给定的激励频率下，通过牛顿迭代法和弧长延拓法进一步求解方程，最终可以求得控制方程的解。

根据文献[3][9][10]选取如表1所示的系统参数，并将相关参数代入整星隔振控制方程，研究耦合系统在振动抑制和能量传递方面的性能。

表1 系统参数

图3为通过谐波平衡-弧长延拓法与四阶龙格库塔法分别求解系统幅频响应得到的结果对比图，研究表明解析解和数值解高度重合，证明了研究方法的正确性。

图3 解析解与数值解

图4给出了双管隔振器对耦合系统的位移幅值响应的结果对比图，NES-双管隔振器耦合系统更好地实现了对卫星主系统的振动抑制，并在固有频率附近将整星系统位移降低到原来的35.2%，进一步提高了系统的减振性能。

图4 系统减振效果图

3 参数分析

图5为外激励幅值A分别是0.0001，0.0002，0.0003m时与主系统位移幅值的结果对比图。研究表明，系统位移随外激励的增大而增大，因此可以通过对比外激励的幅值来研究主系统的减振性能。图6给出了双管隔振器等效阻尼cd分别为100,300和500 Ns/m 时与主系统位移幅值的结果对比图。研究表明，系统位移随着等效阻尼的增大而减小,因此选择合适的等效阻尼参数可以实现更好的系统减振。

图5 外激励与位移响应

图6 等效阻尼与位移响应

双管隔振器工作时的平均功耗为[9]

(4)

图7为外激励幅值A分别是0.0001，0.0002，0.0003 m 时与所需功率的结果对比图。在相同频率下，随着外激励幅值的增加平均功耗随之增加，并在固有频率处达到最大值。研究表明，随着外激励幅值的增大，需要消耗更多的能量来实现系统减振。图8给出了双管隔振器等效阻尼cd分别为100，300和500 Ns/m 时与所需功率的结果对比图。在相同频率下，平均功耗随着等效阻尼的增加而减小，在固有频率处减小的效果更明显。因此，通过增加隔振器流体的压强，可以提高系统等效阻尼的效果，进而在相同功率下可以实现更好的系统减振性能。

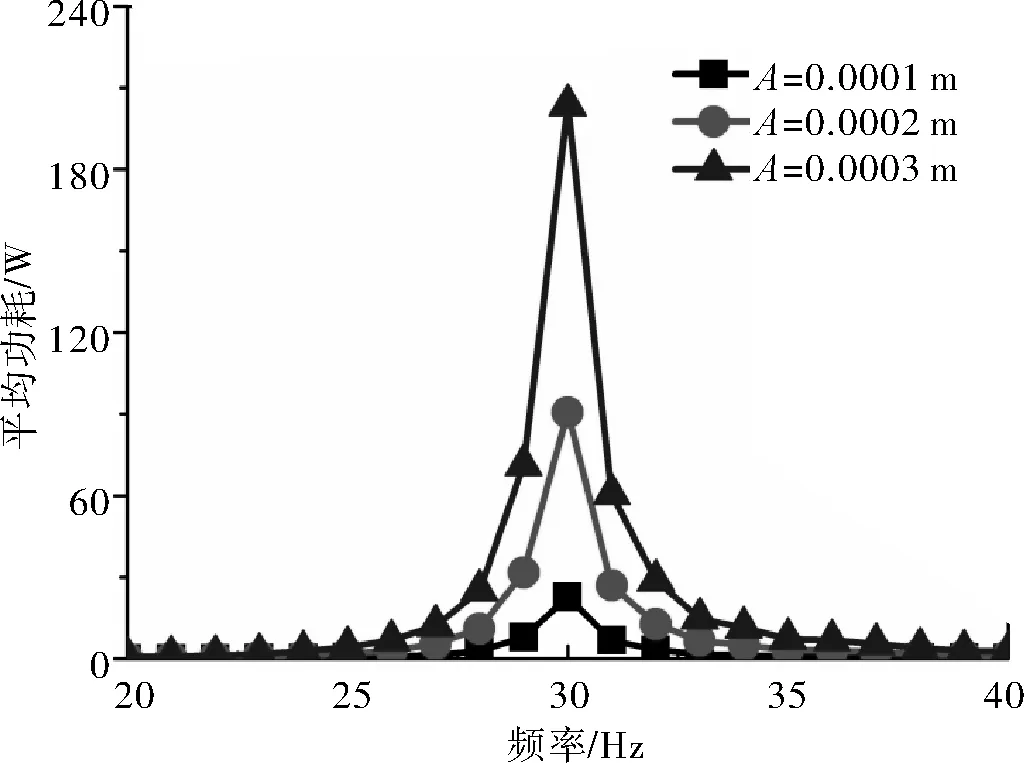
图7 外激励与功率

图8 等效阻尼与功率

4 能量关系

根据能量守恒原理，系统的总能量E(t)表示为[3]

E(t)=Tps(t)+Vps(t)+Wps(t)+TNES(t)+VNES(t)+WNES(t)+ED(t)

(5)

其中：TPS(t)和VPS(t)分别为基础结构响应的动能和势能；WPS(t)为基础阻尼的耗散能。TNES(t)和VNES(t)分别为NES系统的动能和势能；WNES(t)为NES阻尼的能量耗散；ED(t)为双管隔振器等效阻尼耗散能[9]。

各能量计算如下[3,11]：

(6)

(7)

(8)

(9)

(10)

(11)

为了深入研究NES与双管隔振器的内部机理，对系统中输入能量的分布进行了初步的计算。当系统受基础位移激励时，对整星隔振系统进行相关能量计算，基础系统吸收的能量占输入总能量的百分比表示为

(12)

NES-双管隔振器耦合系统吸收的能量占输入总能量的百分比表示为

(13)

图9给出了双管隔振器等效阻尼cd分别为100，300和500Ns/m时与基础能量吸收的结果对比图，在固有频率下基础能量吸收率随等效阻尼的增加而减小。研究表明，适当增加系统的等效阻尼，基础可以传递更多的外激励能量。图10给出了双管隔振器等效阻尼cd分别为100，300和500Ns/m时与耦合系统能量吸收的结果对比图。在固有频率下，耦合系统能量吸收率随着等效阻尼的增加而减小。研究表明，适当增加等效阻尼的参数，耦合系统可以耗散更多机械能，为以后的科学研究提供了参考依据。

图9 基础能量吸收对比

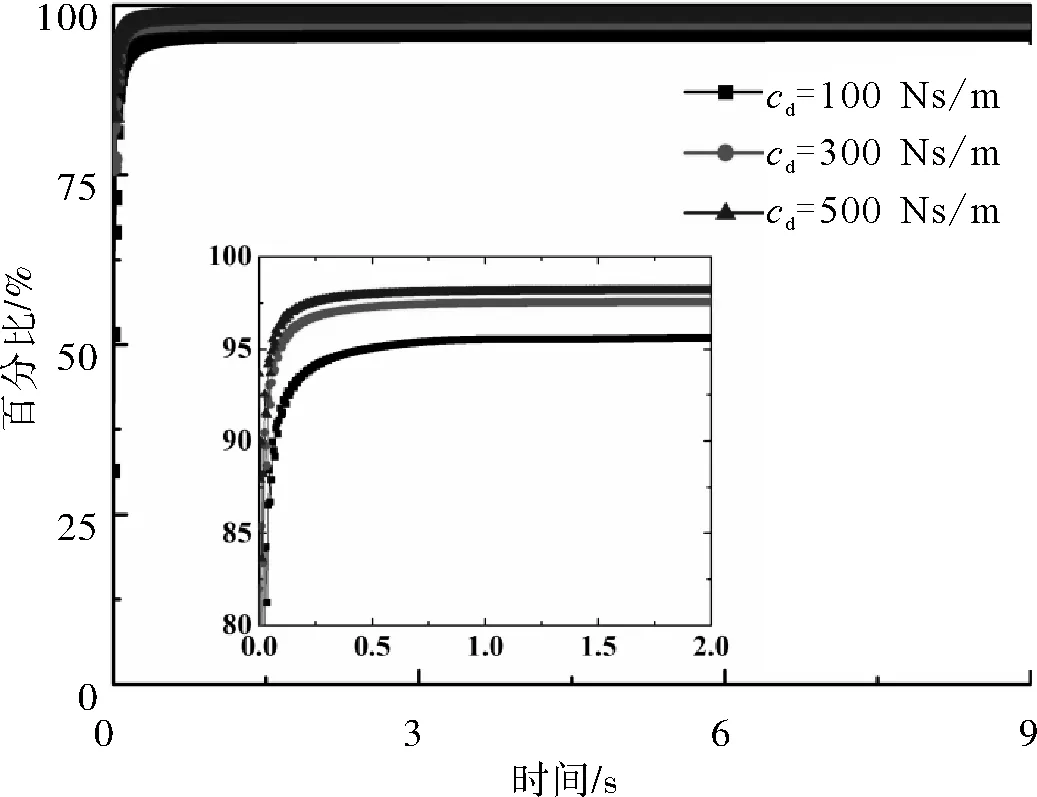
图10 耦合系统能量吸收对比

图11给出了双管隔振器对基础系统能量吸收的结果对比图。在基础系统受到外激励时，NES-双管隔振器耦合系统比单一NES系统更好地实现了对卫星主系统的能量转移，并在9s后提升了5.74%的能量传递效率，表明耦合系统具有更优良的能量吸收性能。

图11 有无隔振器对基础能量吸收的影响

图12相应的给出了双管隔振器对耦合系统能量吸收的结果对比图。在基础系统受到外激励的9s时间内耦合系统吸收了主系统能量的97.60%，NES系统吸收了主系统能量的91.86%，结果表明耦合系统的能量耗散率比单一NES系统提高约5.74%，再次证明耦合系统具有更优良的能量吸收性能。

图12 有无隔振器对耦合系统能量吸收的影响

5 结论

研究NES-双管隔振器一体化耦合系统的非线性动力学响应和能量耗散，通过谐波平衡-弧长延拓法和四阶龙格库塔法验证分析结果的准确性，讨论双管隔振器对主系统位移幅值的影响，并进一步对比分析系统参数对时域和功率的影响，研究耦合系统能量吸收的变化情况。得到以下结论：

(1) 谐波平衡-弧长延拓法的近似解与四阶龙格库塔的数值解高度一致，验证了分析方法的正确性。

(2) 对比分析主系统的幅频响应，结果表明耦合系统比单一NES系统，具有更优良的减振性能。

(3) 研究双管隔振器对系统的能量吸收的影响，结果表明耦合系统的能量吸收率比单一NES系统提高约5.74%。