结合关注事件的时间自动机语言包含模型检测
2020-01-14陈铁明
王 婷,苏 琪,陈铁明
(浙江工业大学 计算机科学与技术学院,杭州 310023)
1 引 言
由Alur等人提出的时间自动机[1]在实时系统的建模和验证分析领域是最重要的模型之一.时间自动机的语言包含问题被描述为,给定两个时间自动机M和N,其中M为系统模型,N为规约模型(即系统需要满足的属性),检查M的时间自动机语言是否包含于N的语言.时间自动机语言包含验证[2]的主要目的是检查系统模型和规约模型(表达系统需要满足的属性)是否存在语言包含关系,即系统行为是否满足某种属性,包括该属性蕴含的时间要求.已经有一些工作将时间自动机相关理论和方法用于实时系统,例如对物联网系统[3]、网络系统控制器[4]、认知机器人系统[5]等的建模和验证,然而大部分方法采用可达性(Reachability)验证、基于时间时序逻辑(例如TLTL[6]、TCTL[7])的验证等方式,目前还没有完善的基于语言包含验证的方法,以应用于实际系统.
由于时间自动机运行时的时间点的无穷性,并不能直接对其进行状态空间搜索.我们之前的工作[2]首次给出了基于时间域抽象(Zone Abstraction)的方法来解决语言包含问题.该方法对无穷时间点进行时间域抽象,求解两个时间自动机的同步积(即状态空间的展开),并将语言包含问题转化成了同步积的可达性问题.然而在实际问题中,系统模型包含大量可能发生的事件,而属性模型一般只需要关注少数几个事件的顺序和时间性.倘若由于语言包含的定义,属性模型必须具有和系统模型同样的事件集合,则会给属性模型的建立带来很大困难.另一方面,通常开发或者测试人员并不熟悉形式化的建模方式,使用时间自动机详细描述验证属性具有一定困难.而为了验证系统正确性及可靠性,模型检查工具必须要以系统和验证属性作为输入.因此,属性模式[8,9]可以用于弥补相关人员和模型检查工具之间的缺口.
围绕上述背景,本文首先在文献[2]的基础上,给出了改进的时间自动机语言包含算法,属性建模时只需考虑关注的事件,简化了属性模型,并且总结了几种常用的时间自动机描述的属性模式,从而能够指导相关人员编写系统需要满足的属性.由于实践中大部分常用的属性复杂度不会很高,并且根据属性模式建立的属性都是可确定化的,该算法具备了较好的实际应用价值.此外,本文还将提出的算法应用于水位控制系统[10]的建模及验证中,并得出了有效结论.
本文章节安排如下.第2节给出时间自动机相关背景知识.第3节详细介绍了时间自动机语言包含验证算法并总结了时间自动机验证常用的属性模式.第4节以水位控制系统为例,应用算法检测系统的一些重要属性.最后是全文总结和未来工作.
2 时间自动机背景
首先给出时间自动机相关定义[1,2].设C为一个时钟集合,Φ(C)表示时钟约束集合.每一个时钟约束定义如下:d:=true|x~n|d1∧d2|d1,其中~∈{=,≤,≥,<,>},x是时钟集合C中的一个时钟,n是一个非负整数.由符号~∈{≤,<}可以获得下行的时钟约束,用Φ≤,<(C)表示.基于C的一个时钟赋值v是指为C中的每个时钟赋予一个实数值.如果v的时钟赋值使得时间约束δ的布尔值为真,则称v满足基于C的一个时间约束δ.对任意d∈R+,令v+d代表时钟赋值v′,使得对所有c∈C都满足v′(c)=v(c)+d.令X代表被重置的时钟集合,[X|→0]v表示所有t∈X都被赋值为零,且其他满足t∈C和t∉X的时钟值仍与v相同.
定义1.(时间自动机)时间自动机是一个六元组A=(S,Init,S,C,L,T),其中S是有穷状态集合;Init⊆S是初始状态集合;Σ是事件集合;C是有穷时钟集合;L:S→Φ≤,<(C)为将状态映射到状态不变式的函数;T⊆S×Σ×Φ(C)×2C×S为带时间约束的转移关系.
基于时间自动机A运行的具体语义,其每个节点是一个(s,v)形式的对,其中s∈S是一个状态,v是一个满足vL(s)的时钟值.A的运行是一个有穷序列Δ=<(s0,v0),(d0,e0),(s1,v1),(d1,e1),…,(si,vi),(di,ei),…>,其中s0∈Init;v0将时钟重置为0;对于所有i≥0都有(si,ei,δ,X,si+1)∈T,使得vi+diL(si),vi+diδ,vi+1=[X0](vi+di)和vi+1L(si+1).给定一个Δ,可以得到其时间语言<(d0,e0),(d1,e1),…,(di,ei),…>.我们用Lan(A)表示所有时间自动机A中的语言.如果两个时间自动机的语言是相同的,那么这两个时间自动机是等价的.
时间域抽象[2](Zone Abstraction)是目前最常用的抽象技术.时间自动机经过时间域抽象后得到一个有穷状态的时间域图(Zone Graph).
一个时间域是由定义在C上的简单线性不等式或线性不等式的合取式结合组成,例如x-y≤5,y>3∧x<7等,其中x,y∈C.给定一个时间域δ,用δ↑表示从δ经过任意时间后得到的时间域.
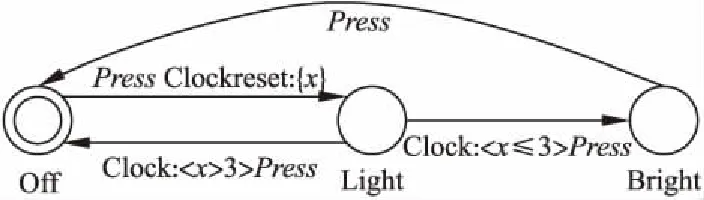
图1 智能灯控的时间自动机模型Fig.1 Timed automaton model of intelligent light control
图1为一个智能灯控系统的时间自动机模型,系统的初始状态为Off,智能灯有Light和Bright两种光线强度.初始状态下,事件Press发生后,系统跳转到状态Light,时钟x重置后开始计时.如果在3个时钟单位内,事件Press再次发生,系统状态由Light跳转到Bright,如果超出3个时钟单位,由于Light上没有状态不变式,系统可以一直停留在该状态,或者经由事件Press跳转回Off状态.除上图中的表达,本文的系统模型还包括如下约定:
1)常量和变量:常量是在模型运行时不会被修改的量,表示如#define A 3,即定义常量A的值为3;变量能够被修改,表示如var B:{0..10}=7,即定义变量B,其初始值为7,取值范围为0到10.
2)信道事件(channel):表示不同进程间发送或接收消息,假设c为信道名,c!表示发送消息,c?表示接收消息[11].
3)转移:其完整表示为,Clock:<时钟约束> [转移条件]事件{操作} Clockreset:{时钟}.在时钟变量满足时钟约束及系统变量满足转移条件的情况下,可以执行事件.事件执行的同时可以发生一些操作,例如改变变量值.Clockreset表示将{}内的时钟重置为零.
3 时间自动机语言包含验证算法
时间自动机语言包含问题定义如下:给定时间自动机M和N,如果Lan(M)⊆Lan(N),那么语言包含成立.我们之前的工作[2]给出了基于时间域抽象(Zone Abstraction)的方法,利用时间域抽象技术,求解两个时间自动机的同步积(即状态空间),并将语言包含问题转化成了同步积上的可达性问题.然而在实际问题中,虽然系统模型和属性模型都为时间自动机,但是系统模型往往包含大量可能发生的事件,而属性模型一般只关注某几个事件的顺序和时间性.因此,我们对该方法进行了改进,使得其在验证时只需考虑关注事件,具体步骤如下.
3.1 验证预处理
根据时间自动机的定义,状态上可存在状态不变式.为了便于同步积上可达状态的搜索,我们首先将时间自动机转换为等价的没有状态不变式的自动机,而不改变其语言[2].该转化将状态的状态不变式移动到该状态的进入和离开的转移上.给定一个时间自动机A=(S,Init,∑,C,L,T),对于任意状态s∈S以及其上的状态不变式L(s),满足:
1)如果(s,e,δ,X,s′)是一个从状态s离开的转移,则将L(s)移动到转移(s,e,δ,X,s′)中,即将其变为(s,e,δ∧L(s),X,s′);
2)如果(s′,e,δ,X,s)是一个进入状态s的转移,对于任意L(s)中的x~n(其中~∈{≤,<},n任意正整数),若x∉X,则将x~n与δ合取,否则忽略该x~n.
给定两个时间自动机M=(Sm,Initm,∑m,Cm,Lm,Tm)和N=(Sn,Initn,∑n,Cn,Ln,Tn).其中N已将状态不变式进行转换(M不需要进行此操作).
3.2 基于时间域抽象的同步积
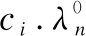
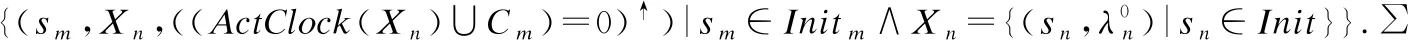
接下来,给定任意节点node=(sm,Xn,δ),通过给出对于非关注事件及关注事件的后续节点的生成步骤来定义T.
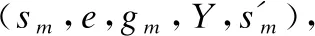
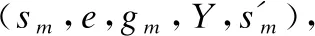

b)由于需要将N进行确定化,Tran(e,Xn)中所有转移的时间约束必须是互斥的.用Exclusive(e,Xn)表示互斥的时间约束集合,集合中每个元素都是一个时间约束.Tran(e,Xn)中的每个转移上的时间约束或取其本身,或取其的否定,然后进行合取.因此,生成的集合Exclusive(e,Xn)中的时间约束一定是互斥的.对于Exclusive(e,Xn)中的每个时间约束,其由所有Tran(e,Xn)中转移上的时间约束本身或其否定组成,如果某个转移并未取否定,则该转移是会发生的.
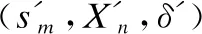

定理1.Lan(M)⊆Lan(N)成立,当且仅当Zone(M⊗N)中不存在可达状态(sm,φ,δ),使得δ为真.

图2的例子完整说明了我们提出的方法如何分步进行.图中M为系统模型,其中h为非关注事件,a为关注事件.N为属性模型,右侧Zone(M⊗N)为时间域图,其初始节点为node0=(m1,{(n1,y)},0≤x=y0).
node1为node0经过事件h的后续节点,m1经过事件h后依然处于m1.由于h为非关注事件,N此时并不需要运行,因此node1中的(n1,y0)与node0相同.时间约束经过条件x>2为2≤x=y0.(步骤1))
当M执行m1到m2的转移,时钟条件为x>3,事件a为关注事件.对于node0中的(n1,y0),基于事件a有两个从n1离开的转移,其时钟条件分别是y>7和y> 3.y的初始活跃时钟是y0,因此将转移((n1,y0),a,y0>3,{y0},(n2,R))和((n1,y0),a,y0>7,φ,(n1,y0))添加到Tran(a,(n1,y0)).转移中的变量将在后续步骤中确定.(步骤 2)中的a))
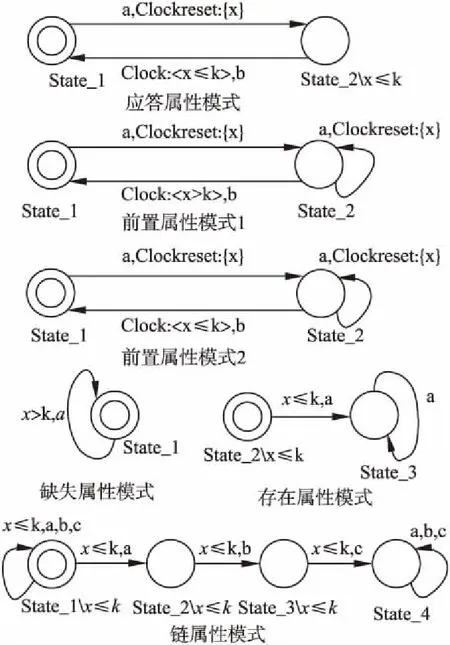
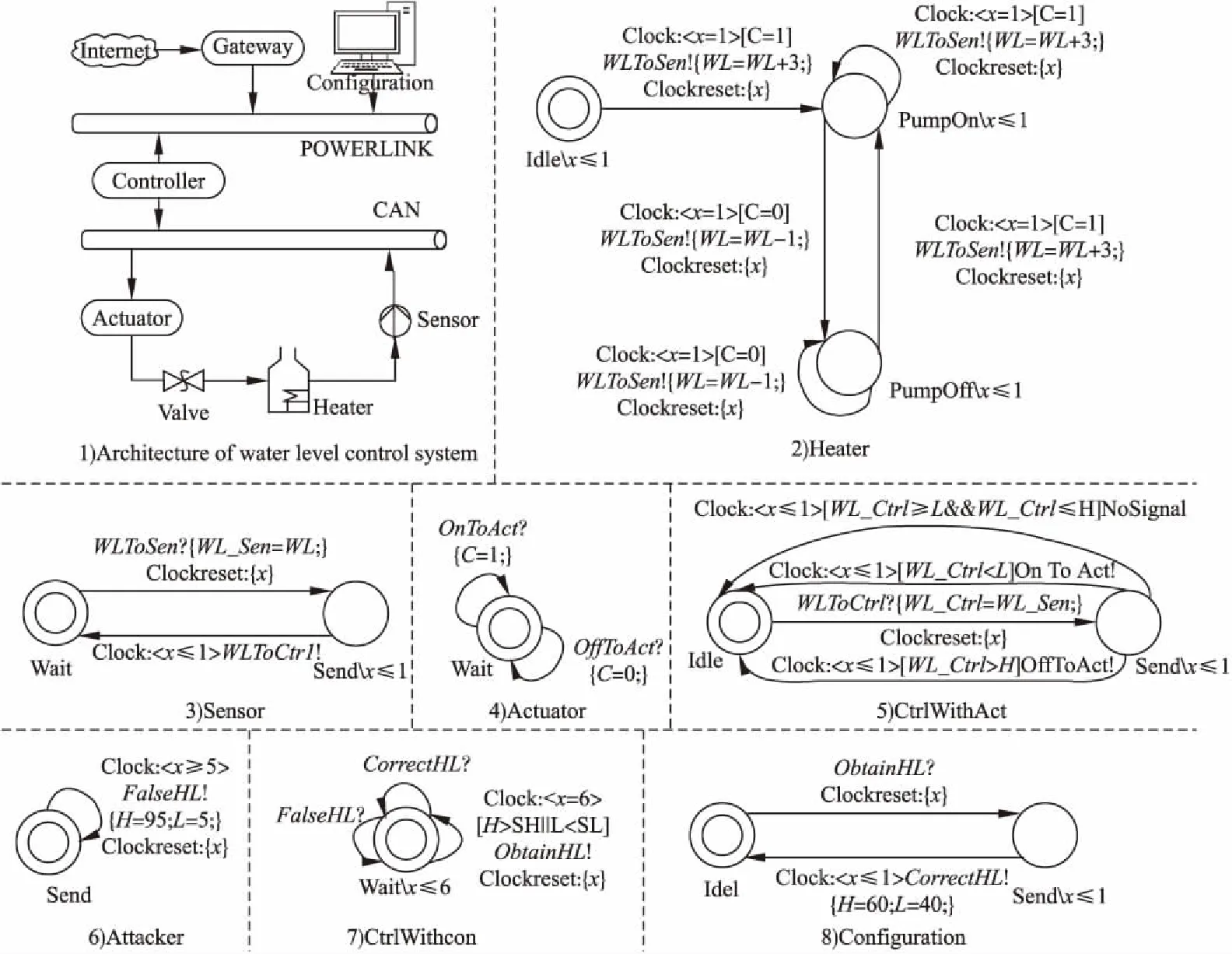
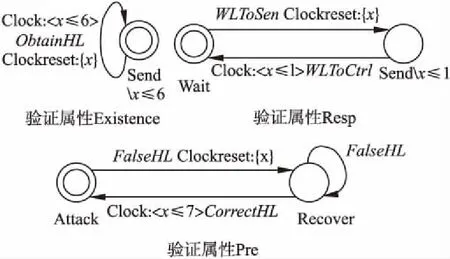
通过使得时间约束互斥的操作,从Tran(a,(n1,y0))可以得到四个时间约束y0>7∧y0>3,y0>7∧y0≤3,y0≤7∧y0>3和y0≤7∧y0≤3,组成Exclusive(a,(n1,y0)).其中y0>7和3 从node0到node2,对于状态n1的回到自身的转移,时钟y0没有被重置,因此(n1,y0)在node2中依然为(n1,y0),时钟y0仍在使用;对于n1到n2的转移,时钟y0被重置,但由于y0在(n1,y0)中需要继续被使用,所以在node2的(n2,y1)中启用新时钟y1(当前R=y1).从node0到node3,只有n1到n2的转移可行,那么可以在node3中重新使用时钟y0.node2和node3中的时间约束是通过node0的初始时间约束、转移时钟条件以及重置时钟情况计算出来的.至此,node0的后续节点构建完毕.(步骤 2)中的c)) 图2 基于时间域抽象的同步积Fig.2 Synchronous product based on zone abstraction 对于到达每个节点时语言包含是否成立的判断,举例来说,node0的Exclusive(a,(n1,y0))中的negAll是y0≤3.0≤x=y0(node0的时间约束),x>3和negAll组合的结果不为真,因此从node0无法生成形如(sm,φ,δ)的节点,其他节点也同样处理(在此例中,M和N的语言包含成立). 算法1.时间自动机语言包含验证算法 输入:时间自动机M和N 输出:验证结果(true或者false) 1.working:=Init; 2.done:=Ø; 3. whileworking≠Ø do 4. removenode=(sm,Xn,δ) formworking; 5. addnodeintodone; 6. ifXn=Ø then 7. return false; 8. end if 10. ife∈Σm∧e∉Σnthen 11. addsucc1(node,Zone(M⊗N)) intoworking; 12. else ife∈Σm∧e∈Σnthen 15. end for 16. end if 17. end for 18.end while 19.return true; 算法1为我们提出的时间自动机语言包含验证算法.算法中有两个数据结构,working存储时间域图Zone(M⊗N)中待搜索的节点,done存储已经搜索过的节点,working的初始值为Zone(M⊗N)的初始状态,done为空集.在从第3行到第18行的循环中,每次将当前节点从working中删除随后添加到done,并且对该节点进行判断(第6行),如果是违反语言包含的节点,则在第7行返回false.第9行到17行判断当前节点的转移事件是否为非关注事件并进行对应操作,若事件e只属于M的事件集合Σm即为非关注事件,则将succ1(node,Zone(M⊗N))的节点加入working;若事件e既属于Σm也属于Σn,则将succ2(node,Zone(M⊗N))中的所有节点加入working.最后,如果搜索完所有状态都没有找到违反语言包含的节点,则两个时间自动机是语言包含成立,此时working为空,并在第19行返回true. 属性模式的建立使用户能够更好地编写出用于自动化模型检查的形式化规范.当前已有研究中的属性模式可以推断事件的发生与否,也能够描述与时间相关的事件发生顺序等逻辑行为[8].然而对于本文中带有状态不变式的时间自动机,尚没有总结出完整的属性模式. 基于时间自动机的属性模式如图3所示,其中a、b、c为事件;x为时钟变量,k为任意正整数.基本的属性模式均为单一时钟变量的时间自动机.实际问题中的验证属性也可以多种模式或者其变体的并行组合,并且可以有多个时钟.文中属性模式的状态上包含的状态不变式,表示系统必须在规定时间离开该状态.以下详细介绍对各个属性模式: 应答属性模式(response),即系统要满足事件b总是紧跟在事件a之后,并且必须在k个时钟单位内发生.State_2上的状态不变式表明了事件b在事件a后发生的必然性.前置属性模式(precedence)与应答属性模式的主要区别在于,事件a发生后,并不强制发生事件b,但是事件b一旦发生,必须在事件a之后,且需要满足一定的时间条件.前置属性模式1表示事件b的发生与a间隔时钟至少为k前置属性模式2表示事件b的发生与a间隔时钟不超过k.由于自循环转移中事件a发生后时钟重置,因此前置属性模式的计时都从a的最后一次发生开始. 图3 属性模式Fig.3 Property patterns 缺失属性模式(absence)表示系统开始运行后,事件a只能在k个时钟单位后发生;事件a也可以永远不发生,即系统一直停留在状态State_1(State_1上没有状态不变式).存在属性模式(existence)表示系统开始运行后,事件a必须在k个时钟单位内发生(由于State_2的状态不变式x≤k,系统无法一直停留在State_2). 链(chain)属性模式表示系统开始运行后,在k个时钟单位内,事件a、b和c必须顺序发生一次.其中三个状态上的状态不变式,表示在k单位时间内无论a、b和c如何发生,最终必须离开这该状态,且到达State_4(处于该状态说明三个事件已经按照顺序发生过一次). 根据[2]所述,3.2节中Zone(M⊗N)的节点数量可能是无穷的,这是由于某些情况下,在确定化N的过程中,有可能产生无穷多的时钟,使得状态持续增长、无法终止.值得庆幸的是,本节的属性模式都是可以被确定化的,因此利用属性模式建立的系统被检测属性在验证时并不会产生上述情况.在实际系统的建模和验证中,大部分属性都可以套用属性模式(或者变种),侧面反映了我们提出的改进方法的可行性. 本章以水位控制系统[10]为例,给出我们提出的算法的应用,算法基于模型检测工具PAT[12]实现.首先使用时间自动机对系统进行建模,其次依据属性模式给出待验证属性的描述,最后得出验证的结果.该案例建模及验证均运行于PC(2.71GHz Intel(R)Core(TM)i5-7200 CPU,8.0GB的RAM). 图4 水位控制系统架构及其系统模型Fig.4 Architecture and models of water level control system 图4为水位控制系统架构及其系统模型,图中1)为水位控制系统架构图,2)-8)为系统各个组件的时间自动机模型图.系统日常运行主要包含5个组件:执行器(Actuator)、控制器(CtrlWithAct和CtrlWithCon)、储蓄池(Heater)、传感器(Sensor)和组态站(Configuration).储蓄池的容量为100,蒸发下降1.组态站设置最高(SH=90)和最低(SL=10)的安全水位.控制器确保水位在正常范围内(L=40<水位 #define SH 90; //最高水位值 #define SL 10; //最低水位值 varWL:{0..100}=50;//储蓄池水位值 varWL_Sen:{0..100}=0; //传感器存储的水位值 varWL_Ctrl:{0..100}=0; //控制器存储的水位值 varH=60;//安全高水位值 varL=40;//安全低水位值 varC=1;//水泵开关控制变量,1表示开,0表示关 channelWLToSen; //发送给传感器的水位值 channelObtainHL;//获取安全水位值 channelFalseHL;//错误的安全水位值 channelCorrectHL;//正确的安全水位值 channelOffToAct;//阀门关闭 channelOnToAct;//阀门打开 channelWLToCtrl;//发送给控制器器的水位值 根据我们提出的属性模式,针对水位控制系统模型建立待验证属性,如图5所示,以下进行详细介绍. 1)验证属性Resp用来检测传感器接收到水位值消息WLToSen后,能否在一个时钟单位内将消息WLToCtrl发送给控制器,以保证消息的实时性.其在PAT中的验证语句为:#assert System refines 2)验证属性Pre验证语句为:#assert SystemWithAttacker refines 3)验证属性Existence为属性模式Existence的变体,其验证语句为:#assert SystemWithAttacker refines 图5 待验证属性的时间自动机模型Fig.5 Timed automaton models of property to be verified 我们在PAT工具中实现了本文的时间自动机语言包含算法,使用该算法进行模型检测后的验证结果数据如表1所示,并可分析出以下结论: 表1 验证结果数据 属性验证结果状态数转移数运行时间(秒)Resptrue1842300.01Pretrue36094718367.30Existencetrue33889673756.82 1)如果将Resp属性的时间约束条件x≤1改为x<1,则验证结果为假,表明该系统模型中的传感器能够在接收到消息后不超过1个时钟单位发送消息给控制器. 2)若将Pre属性中的时间约束条件x≤7改为x≤6,则验证结果为假,表明系统在有攻击者的情况下,水位正常范围被篡改之后,最终总是能够在不超过7个时钟单位恢复.这一验证属性表明系统的恢复机制是有效的. 3)Existence属性的验证结果表明系统受到攻击后,能够在不超过6个时钟单位及时获取正确值. 需要注意的是,本文算法改进的目标在于需要验证的属性在建模时不必关注无关事件,从而大大简化了建模方式.算法在改进前后运行时访问的状态空间是一致的,进而访问的状态和转移数量是相同的,因此运行时间和效率也是一致的. 本文对已有的时间自动机语言包含检测算法进行了优化,只需要关注与验证相关的事件及其发生先后顺序、时间条件等,而不必考虑与验证属性无关的事件,简化了待验证属性的建模,并且总结了基于时间自动机的常用属性模式.此外,本文还以水位控制系统为例,展示了我们提出的方法,包括系统模型、属性模型和验证结果. 关于未来工作,一方面将研究时间自动机语言包含算法的优化问题,例如减少状态空间的方法,性能及运算效率的提高;另一方面继续探索属性模式和语言包含算法如何更好地解决实际问题.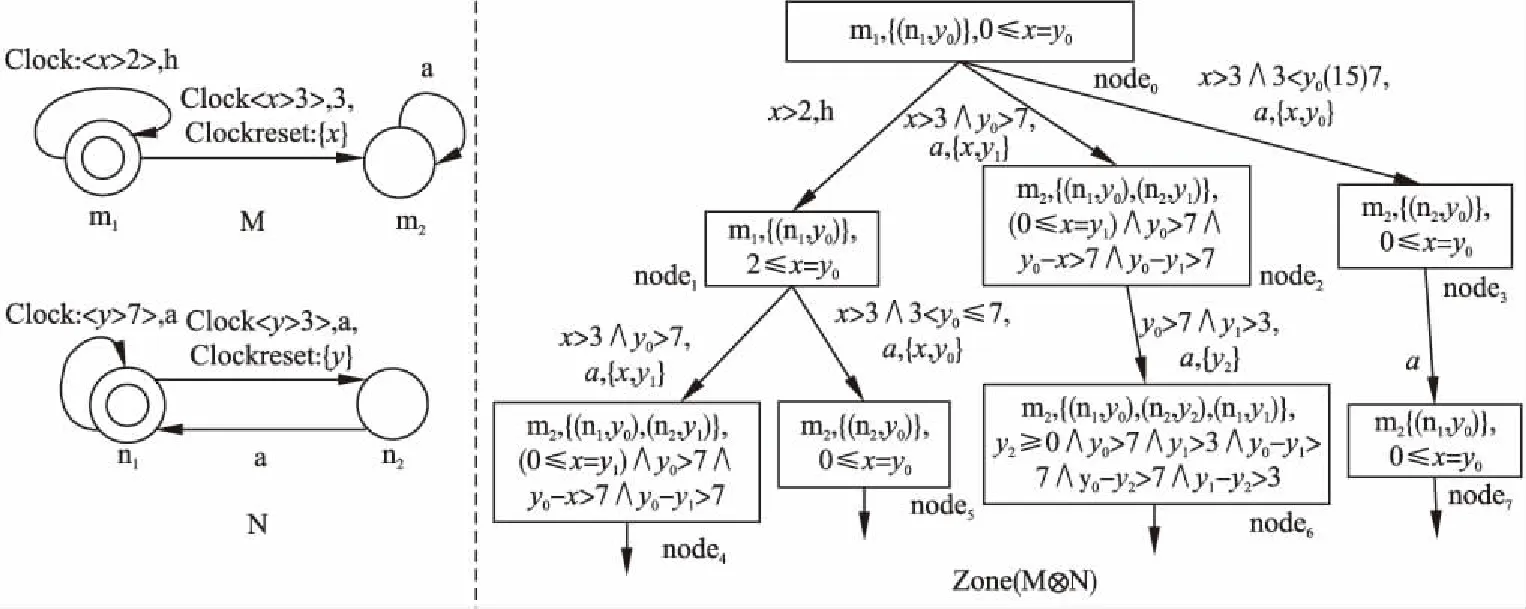
3.3 时间自动机语言包含验证算法
3.4 基于时间自动机的属性模式
4 案例分析
4.1 水位控制系统建模
4.2 待验证的属性描述
4.3 验证结果
Table 1 Data for verification results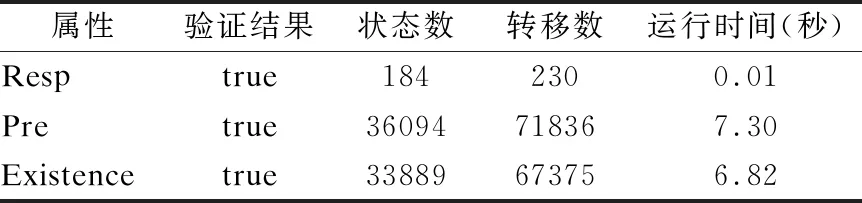
5 结束语
