基于Stacking策略的过程剩余执行时间预测

李帅标,赵海燕,陈庆奎,曹 健

1(上海理工大学 光电信息与计算机工程学院,上海市现代光学系统重点实验室,光学仪器与系统教育部工程研究中心,上海 200093)2(上海交通大学 计算机科学与技术系,上海 200030)

1 引 言

为了提高运营效率,降低成本,提高客户服务质量并降低人为错误的可能性,越来越多的公司采用过程感知信息系统(Process-Aware Information Systems,PAISs)来支持其业务流程,同时以事件日志的形式记录每个执行活动的踪迹.这一转变致使企业积累大量数据,为了提高企业效益,从海量数据中提取有用信息预测业务过程实例这一趋势得到很大发展.

目前已经提出很多用于预测业务过程实例行为的方法[1,2],比如预测业务过程风险或者业务过程剩余执行时间等.对于业务过程风险而言,这些预测可帮助过程管理者识别出具有风险的过程实例并提前给出解决方法以减少损失,比如资源重新分配或人工干预等.同样,业务过程剩余执行时间对过程管理者或用户体验非常重要,比如客户在银行办理业务时,提供预测结束时间对客户满意度有积极影响.

近年来,研究者提出了一些方法以对业务过程剩余执行时间进行预测.但是现有预测方法主要采用了黑盒模型,它们是通过历史事件日志文件构建一个整体模型,然后将模型输出值作为预测的剩余时间值.虽然现有技术能够预测业务过程活动剩余时间值,但是没有解释后续活动的信息是如何影响预测的时间总值的.比如对一个简单的串行业务过程实例A→B→C→D而言,假设当前业务过程执行到B,如需预测活动B的剩余时间,黑盒方法则利用历史记录训练模型直接预测活动B到达活动D的剩余时间,而不考虑活动C对剩余时间的影响.一些学者在对业务过程时间预测研究的实验结果表明考虑上下文信息对预测效果有积极影响[3],所以考虑活动C的相关特征应该能够对预测结果准确性的提高有积极影响.另外,业务过程活动作为时间序列活动,活动之间存在的依赖关系对结果也有很大影响.

为了考虑各个活动对剩余时间的影响以及活动之间的关系对最终预测结果的影响,我们提出一种基于Stacking策略的模型融合(Stacking Strategy for Model Fusion,SSMF)的白盒方法用于业务过程剩余时间的预测.该模型由两部分组成,第一部分引入朴素贝叶斯(Naive Bayes,NB)模型用于计算当前状态选择下一个活动的概率,引入支持向量回归(Support Vector Regression,SVR)用于计算当前活动状态到达下一活动状态花费的时间;第二部分将当前活动预测所有可能的分支概率与分支时间作为训练集,对长短期记忆(Long Short-Term Memory,LSTM)神经网络模型进行训练;最后模型预测结果即为当前活动剩余执行时间.

本文后续内容组织安排如下:第2节介绍近年来业务过程时间预测的研究方法;第3节介绍SSMF算法的基本思想、本论文中使用的相关机器学习技术以及SSMF模型的具体实现过程,第4节阐述相关实验与分析,第5节是对全文进行总结以及未来工作方向的分析.

2 相关工作

近年来,业务过程的剩余时间预测问题已经被很多学者所研究.Aalst等人在文献[4]中提出了第一个侧重于时间视角的预测方法,该方法从历史事件日志信息构建带有标注的变迁系统(An Annotated Transition System),为了预测业务过程的剩余完成时间,使用状态表示函数将到目前为止执行的活动序列映射到变迁系统中的一个状态,并通过基于类似状态下的较早的过程实例的平均完成时间来进行预测.文献[5,6]中提出了一种在文献[4]中描述技术的扩展方法,他们根据“上下文特征”对日志文件中的踪迹进行聚类,然后,对于每个聚类,他们使用文献[4]中描述的方法创建预测模型.对于新的运行实例,使用预测聚类树对其进行聚类,然后使用属于特定聚类的模型进行剩余时间的预测.在文献[7]中,Bolt等人则提出一种称为查询目录的新方法,为了计算新的部分踪迹尾部(Partial Trace Tail)的剩余时间,将其与查询目录(Query Catalogs)中存储的部分踪迹尾部进行比较,将匹配的部分踪迹尾部的平均剩余时间作为剩余时间预测值.文献[8]中,Polato等人使用了一种ε-SVR机器学习算法对业务过程进行剩余执行时间的预测.该方法使用业务过程的历史踪迹活动属性信息训练ε-SVR模型,并通过编码技术将部分踪迹的特征转换为适合模型输入的格式,输出的值即为估计的剩余执行时间.Navarin等人[9]提出了一种基于LSTM神经网络模型对剩余时间预测的方法,其特点是学习长期的依赖关系.它将历史完整踪迹中各活动信息通过编码技术转换为支持LSTM输入的特征向量进行模型的训练,最后将未完成的踪迹信息输入模型之中进行时间的预测.

上述方法虽然考虑了活动特征对结果产生的影响,但是并没有考虑单个活动对最终预测结果能够产生的影响大小.另外,文献[9]中虽然考虑了活动之间的依赖关系,但是其学习对象为已经发生的活动,与本文有所区别.本文中的LSTM神经网络是从后续还未发生的业务过程活动对象中学习长期依赖关系.基于上述描述,我们提出一种SSMF模型来预测当前正在执行业务过程的剩余时间.另外,实验结果表明该模型考虑更多的上下文特征,其预测结果具有更高的预测精度.

3 基于Stacking模型融合策略的业务过程剩余时间预测算法

3.1 算法思想介绍

在真实的业务流程执行过程中,当某个活动结束后,其后续可能包含多条分支路径,为了展示单个活动或基本元素以及活动之间存在的“上下文”对整体结果的影响,我们的算法思想可分为两步.第一步对单个活动对最终预测效果的影响程度进行学习.为了解决这个问题,我们根据NB与SVR预测当前活动选择后续活动的概率与到达各活动的执行时间,对当前活动后续所有分支路径上的活动进行同样的操作以获取当前活动点所有可能值(概率与时间值)组合.第二步依据已获取的信息估计当前活动的剩余时间.通过对最大概率路径时间预测、期望值时间预测以及真实执行路径时间预测等几种不同方法的分析,我们发现在每一个活动处,根据已经获取的各种可能的信息组合对活动剩余时间的预测可能是一个非线性的模型.神经网络能够很好的解决非线性问题[10],同时能够学习活动之间存在的依赖关系,所以我们选用神经网络模型用于预测剩余时间.

本文所提模型目的用于预测当前活动剩余执行时间,由于只有部分活动得到了执行,后续的执行路径还是不确定的,因此,模型首先使用NB与SVR预测其后续可能选择活动的分支概率与执行时间,这是一种用于统计当前活动点后续所有可能特征的方式,为训练后续模型做准备.其次,将当前活动点所统计的所有分支概率与各个活动之间的执行时间作为LSTM模型的输入特征,并通过训练好的LSTM模型用于预测当前活动点的剩余执行时间.

基于上述描述,我们提出一种基于Stacking模型融合策略的业务过程剩余执行时间预测方法.为了更好的理解算法基本思想,我们通过图1对其作出解释.

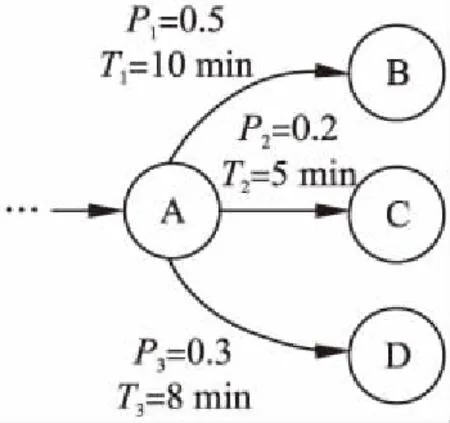
图1 模型执行过程解析图Fig.1 Analysis of the model execution process

如图1所示,假设业务过程活动执行到活动A,且其后续可能的活动为B,C,D.第一步:根据已经训练好的NB与SVR模型预测其后续可能选择活动的分支概率与执行时间,其中P1,P2,P3值表示活动A选择后续活动B,C,D的概率,T1,T2,T3值用于衡量从活动A到达后续活动B,C,D的估计时间.第二步:根据第一步计算的结果,将{P1,P2,P3,T1,T2,T3}作为输入特征输入活动A所对应的已训练结束的神经网络模型,其输出结果即为活动A的预测剩余执行时间.

3.2 机器学习技术介绍

本节主要介绍在本篇论文中运用到的机器学习技术与相关知识.

3.2.1 朴素贝叶斯分类器

朴素贝叶斯分类器是一个基于贝叶斯定理应用的概率分类器,它可以预测给定样本属于特定类的概率.贝叶斯定理数学公式如公式(1):

(1)

其中P(A)表示A的先验概率,P(B)表示B的先验概率.朴素贝叶斯则是借助上述思想计算概率,具体实现过程如下:

1)假设T表示训练样本集合,每个样本都有对应的类别,类别集合Y={y1,…,yk}.每个样本由n维向量表示,X={x1,…,xn}用于描述n个属性的n个测量值.

2)给定样本X,朴素贝叶斯分类器借助公式(2)预测X属于具有最高后验概率的类.

(2)

其中,P(X)对于训练集中所有类别而言,其值是一样的,因此计算过程只需考虑P(X|Yi)P(Yi)的结果.另外,朴素贝叶斯分类器假设属性值对给定类的影响与其他属性值无关.故P(X|Yi)可转化为公式(3):

(3)

3)对于样本X,根据公式(4)找出所有类别中最大后验概率值,并将该类别作为样本X的预测类别.

P(yi|X)=max{P(y1|X),…,P(yk|X)}

(4)

3.2.2 支持向量回归

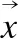
为了说明支持向量回归机的基本思想,通过线性回归函数对其简要介绍.表达形式见公式(5).

(5)

(6)

一般引入拉格朗日函数将优化问题转为其对偶形式:

(7)

(8)

对于不能用线性函数进行回归的训练数据,利用核函数将训练集映射到高维空间之后再进行线性回归.

3.2.3 LSTM神经网络

LSTM神经网络是一种改进的循环神经网络(Recurrent Neural Networks,RNN)人工智能算法,LSTM对时间序列相关数据的处理有很好的效果[12].LSTM模型可以记忆更长的上下文[13].目前图2中的LSTM细胞应用最为广泛[14].

图中123标号分别表示遗忘门、输入门以及输出门.

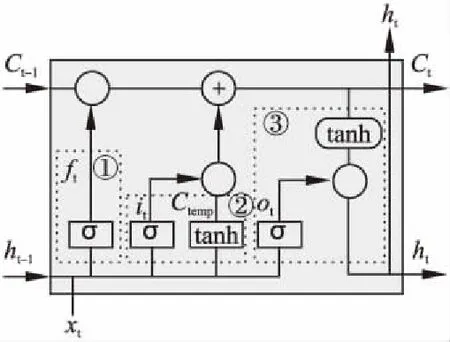
图2 LSTM隐藏层细胞结构Fig.2 LSTM cell structure in hidden layer

遗忘门:其功能用来决定从细胞状态中抛弃何种信息.该门读入当前时间点的输入xt以及上一层细胞的输出ht-1,通过公式(9)计算ft值并将其赋值给当前细胞状态Ct-1.其中1表示保留其信息,0表示舍弃其信息.

ft=σ(Wf*[ht-1,xt]+bf)

(9)

输入门:其功能用来决定多少新的信息添加到细胞状态中.该过程包含两部分,第一部分:通过sigmoid函数决定哪些输入需要添加到细胞状态中,另外通过tanh函数生成候选向量值用来更新细胞状态.第二部分:更新旧细胞状态Ct-1为新状态Ct.计算公式见公式(10)-公式(12).

it=σ(Wi*[ht-1,xt]+bi)

(10)

Ctemp=tanh(WC*[ht-1,xt]+bC)

(11)

Ct=ft*Ct-1+it*Ctemp

(12)

输出门:其功能用来决定最终输出哪些信息.该门运行过程分为两步,第一步:通过公式(13)决定细胞状态Ct中的哪些信息被输出;第二步:对细胞状态使用tanh处理得到结果并与第一步的结果相乘,以确定最终输出的信息,计算公式见公式(14).

ot=σ(Wo*[ht-1,xt]+bo)

(13)

ht=ot*tanh(Ct)

(14)

3.3 SSMF模型框架

模型融合通过对不同模型结果的融合得到一个新的结果,该结果将取代各个原始模型的预测结果.Stacking策略是由Wolpert[15]等人提出的一种对分类器叠加组合思想的方法.该方法首先提取有效特征进行第一次的训练和预测,并将该操作视为第一层,其次将第一层训练的结果采用合适的融合方法进行二次训练与预测,即第二层的训练与预测,以获得更为精确的预测结果[16].本文利用Stacking策略的思想,出于对单个活动对结果的影响以及活动之间存在的依赖关系的考虑,提出一种业务过程剩余时间预测算法,其模型结构如图3所示.

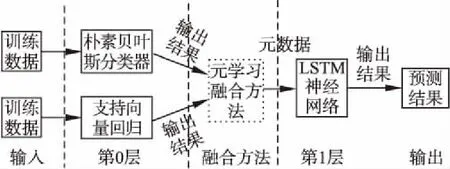
图3 Stacking模型融合结构图Fig.3 Stacking model fusion structure

图3表明本文所提模型共包含两层结构:第0层结构与第1层结构.第0层结构由朴素贝叶斯分类器与支持向量回归构成,第0层结构里包含的模型通常被称为基分类器或基回归器,基分类器与基回归器的输出结果将作为第1层的输入数据.第1层结构由LSTM神经网络构成,通过对第0层的输出结果进行训练以预测剩余时间.因该层输入的数据是一种通过融合方法产生的元数据,故第1层也被称为元数据分类器或回归器.在获取第0层的输出结果后,需要采用一定的方法对输出结果进行融合,融合方法可以分为两种,固定融合方法(Fixed Rules,FR)和可训练融合方法(Trained Rules,TR)[17].本文模型中采用的是一种流行的元学习(Meta-learning)可训练融合方法,它是一种将上一层输出结果作为中间特征[18](元数据)的方法.即对第0层的各个输出结果进行组合作为第1层模型的输入特征.

上述框架共经过两次训练,两次训练即相互独立又相互关联.独立指的是两次训练都是单独训练互不影响,关联指的是上一层模型的输出作为下一层模型的输入.

3.4 SSMF模型实现过程

本小节对模型的实现过程进行详细介绍,首先介绍SSMF中各个子模型的运行过程,然后对其整体运行流程进行描述.

3.4.1 NB模型的使用

朴素贝叶斯分类器应用于SSMF模型第0层,首先将已经预处理的数据划分为训练集与测试集;然后以业务过程活动开始执行到当前活动获取的信息作为训练输入特征,将当前活动真正选择下一活动作为训练输出目标,训练当前活动NB模型,并用于预测当前活动选择下一可能活动的概率.业务过程活动继续执行,为了提高预测的精度,需要将已执行的活动特征添加到数据集中,采用上述方式统计各个活动点可能选择下一活动的概率,直至业务过程活动执行结束.

3.4.2 SVR模型的使用

支持向量回归器应用于SSMF模型第0层,首先将已经预处理的数据划分为训练集与测试集;然后以业务过程活动开始执行到当前活动获取的信息作为训练输入特征,将当前活动执行到下一活动的真实时间作为训练输出目标,训练当前活动SVR模型,并用于预测当前活动执行到下一可能活动的时间.业务过程活动继续执行,为了提高预测的精度,需要将已执行的活动特征添加到数据集中,采用上述方式统计各个活动点可能到达下一分支活动的执行时间,直至业务过程活动执行结束.

3.4.3 LSTM模型的运用

长短期记忆神经网络应用于SSMF模型第1层,该层主要应用于预测当前活动的剩余执行时间.根据3.4.1小节与3.4.2小节中所述,在当前业务过程活动状态处可统计其后续所有可能选择的分支概率与执行时间,并将其组合结果作为训练LSTM模型的输入特征,将业务过程当前活动真正结束时间作为训练LSTM模型的输出目标.通过上述方式,训练不同活动点的时间预测模型.

3.4.4 整体过程描述

1)获取有效特征.根据已有的事件日志文件,通过数据预处理、特征筛选、特征提取等步骤获取对活动时间有影响的活动特征.

2)训练模型第0层中朴素贝叶斯分类器.根据3.4.1小节运行过程所述对不同活动点处朴素贝叶斯分类器进行训练,并将训练好的模型应用于测试集中,预测当前活动选择下一个可能执行活动的概率.

3)训练模型第0层中支持向量回归器.根据3.4.2小节运行过程所述对不同活动点处支持向量回归器进行训练,并将训练好的模型应用于测试集中,预测当前活动到达下一个可能执行活动的时间.

4)训练模型第1层中LSTM神经网络模型.当步骤(2-3)执行结束后,采用3.4.3小节所介绍训练方式,对业务过程不同活动点处训练各自的神经网络模型.

5)预测剩余时间.对测试集的业务过程实例,利用对应活动点已经训练好的NB模型与SVR模型用于预测其可能选择下一活动的概率与到达下一活动的执行时间,并将统计的信息作为对应活动点神经网络模型的输入特征,其输出结果即为预测当前活动剩余执行时间值.

4 实验与结果分析

4.1 实验数据

本文所使用的数据集来自于2017年业务过程智能(Business Process Intelligence,BPI)挑战赛,该数据集包含了2016年1月-2017年2月期间荷兰金融机构贷款申请流程的真实业务流程,其特征包含活动类型,活动执行者,时间戳以及其他信息,比如申请的金额和贷款目的等.该数据集中包含多次创建报价的业务过程实例,为了简化实验过程,故只考虑创建一次报价且信息验证不超过两次的业务过程实例.整理后的实验数据包含22900条贷款申请实例与169457个活动.

4.2 实验数据分析

贷款申请过程由一系列活动构成,数据集中贷款申请可能的执行路径如图4所示.

图4表示当前数据集中所有可能执行的路径及结果,其中相关活动名称介绍见表1,后续相关实验以该过程模型为基础.

在实验部分,我们假设当前业务过程活动执行到活动A_Concept,在此基础上预测过程实例在活动A_Concept的剩余执行时间以及后续活动节点的剩余执行时间.

图5描述的是数据集中业务过程活动中两个相邻活动时间间隔的分布,其中Duration_1表示活动A_Concept到活动A_Accepted的时间间隔分布,后续活动间隔以此类推.由图观察可知,不同活动间隔的时间分布有所差异,这种不同活动时间间隔差异可看做活动之间存在某种关系.神经网络在不同活动之间学习长短期依赖信息有很好效果,这也是本文使用神经网络作为模型训练的原因.

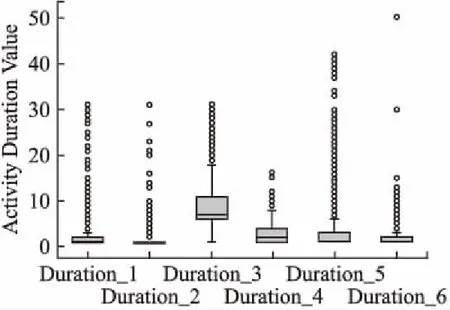
图5 活动间隔时间分布Fig.5 Activity interval distribution

4.3 评价指标

为了检验模型的有效性,本文使用均方根误差(Root Mean Squared Error,RMSE)作为评测指标.RMSE计算实际观测值与预测值之间的标准差,其值越小表示模型预测的结果要好.计算公式如下:

(15)

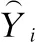
4.4 方法比较

为了验证所提方法的预测精度,将其与部分业务过程剩余时间预测方法进行比较.在本文中使用历史平均值(Mean Value,MV)方法、最大概率路径(Maximum Probability Path,MPP)预测方法、真实执行路径(Real Execution Path,REP)预测方法、期望值(Expected Value,EV)预测方法以及支持向量回归方法与所提出方法进行比较.

表1 活动名称说明
Table 1 Activity name description

活动名称说明A_Submitted客户提交新的贷款申请A_Concept系统自动完成第一次评估A_Accepted对申请的客户提供贷款金额A_Complete贷款金额发送给客户,银行等待客户退回已签名文件(工资单或身份证等)A_Validating银行对收到的文件进行检查A_Incomplete文件信息缺失,需要客户重新发送文件A_Pending银行收到所有文件并且评估结果为正,为客户提供贷款A_Cancelled客户从未发送过文件或电话咨询客户被告知不需要贷款,贷款申请被取消A_Denied客户申请条件不符合银行检验标准,贷款申请被拒绝

对上述部分比较方法进行说明:

1)MPP方法对业务过程活动中每个活动使用NB与SVR模型预测当前活动选择下一个可能活动的概率与达到下一个活动的执行时间.在每个活动点上利用概率乘积的方式统计每个活动点所有可能执行路径的概率,并选取概率值最大的活动组合作为当前活动执行路径,并将该路径中各个活动预测执行时间求和作为其预测值.

2)REP方法利用SVR模型预测活动执行时间,将当前业务过程实例真正的执行路径作为预测执行路径,并计算各个活动执行时间总和作为预测总值.

3)EV方法首先统计当前业务过程实例在各个活动点选择不同结果的概率与剩余执行时间,到达不同结果的概率与剩余执行时间计算采用加权求和方式,然后根据前者计算的结果,再次利用加权求和方法求取不同活动点的剩余执行时间.虽然两次计算方法均采用加权求和,但是所执行的对象不同.

4)SVR方法将业务过程执行开始到当前活动已获取的特征作为输入,将当前活动执行至业务过程结束的真实时间作为输出进行模型训练.对训练结束的模型,输入已获得活动特征,输出值即为当前活动的预测剩余时间.

4.5 对比试验分析

本文搭建的SSFM模型运用到朴素贝叶斯、支持向量回归以及LSTM神经网络.其中LSTM参数部分对结果影响较大,因此对LSTM神经网络部分进行介绍.本文搭建的LSTM神经网络模型包括输入层、隐藏层以及输出层,其中误差函数使用均方误差(mean squared error,mse),优化算法使用适应性动量估计(Adaptive moment estimation,Adam)算法,它是由Kingma等人提出[19].Adam是一种基于梯度的随机优化算法,其优点是能够自适应性更新学习率,且在实际应用中效果很好[20].

为了防止模型学习不充分或过拟合,我们在不同迭代次数处输出损失函数值以选择合适的迭代次数,各个活动迭代次数损失函数输出值如图6所示.

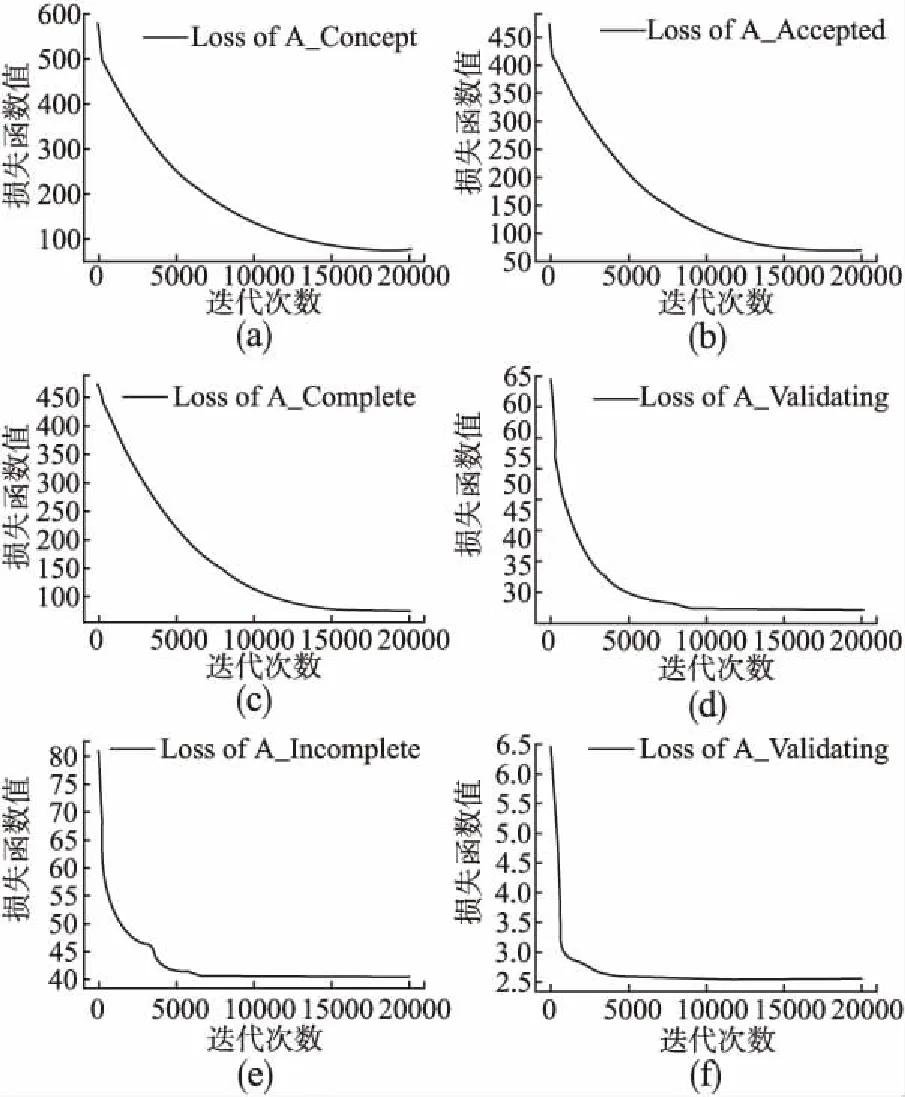
图6 不同迭代次数的损失函数值Fig.6 Loss function values for different iterations

图6表示不同活动点迭代次数与损失函数值的关系,通过图6(a)发现在活动A_Concept处当迭代次数达到17500左右,损失函数值趋于稳定,故将17500设置为当前活动的迭代次数.同理,由图6(b)-图6(f)观察可知,后续活动迭代次数分别设置为15000,15000,8000,6000,3000.

本文通过上述参数学习不同活动点网络模型,并对数据集按照8:2划分为训练集与测试集对算法进行试验,本文所提方法与对比实验结果如表2所示.

表2 不同预测方法的RMSE值
Table 2 RMSE values for different prediction methods

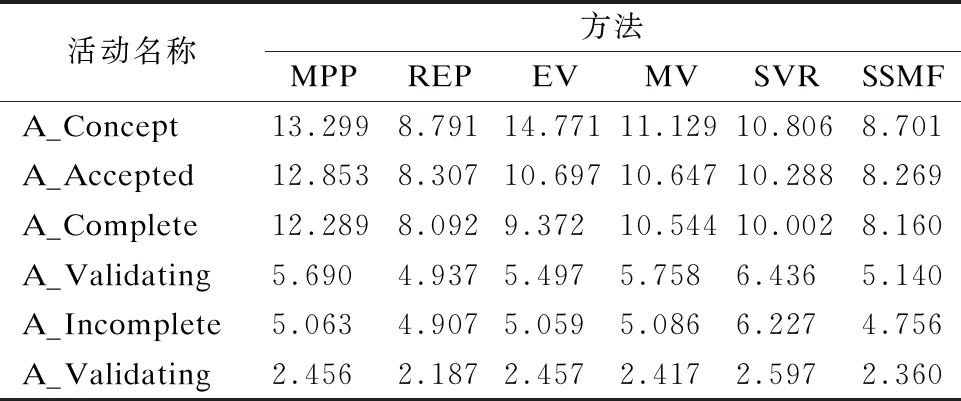
活动名称方法MPPREPEVMVSVRSSMFA_Concept13.2998.79114.77111.12910.8068.701A_Accepted12.8538.30710.69710.64710.2888.269A_Complete12.2898.0929.37210.54410.0028.160A_Validating5.6904.9375.4975.7586.4365.140A_Incomplete5.0634.9075.0595.0866.2274.756A_Validating2.4562.1872.4572.4172.5972.360

对比实验REP将业务过程的真正执行路径作为其预测执行路径,而其他对比实验则不知道真正的执行路径,故其实验结果可作为其他方法的参考标准, 即其他方法的实验结果与REP结果越接近表明该方法预测效果越好.由表2可知,本文提出的SSFM算法在不同活动点的预测精度都比其他对比算法较高.对所有方法而言,其预测误差随着活动执行逐渐变小,进一步说明考虑更多活动上下文对预测结果有积极影响.另外实验结果表明SSMF预测结果与REP预测结果最为接近,且在个别活动点其预测效果更好,即表明SSFM预测结果与业务过程实例的真正执行路径时间较为接近,更好的解释了SSFM模型的学习活动之间依赖信息的能力以及考虑各个活动对整体结果具有积极作用.

5 总结与展望

本文结合朴素贝叶斯、支持向量回归以及LSTM神经网络模型,提出基于Stacking策略模型融合的业务过程剩余执行时间预测方法.该方法具有以下优点:1)该方法考虑更多的上下文特征对预测结果的影响;2)该方法考虑基本组件或单个活动对整体结果所做的贡献与影响;3)该方法考虑各个活动之间存在依赖关系.另外,将本文所用方法与相关业务活动剩余时间预测方法进行比较,在以RMSE作为评价指标的前提下,发现该模型具有更高的预测精度,具有更好的表现效果.本文使用的模型只应用于预测当前活动的剩余执行时间,业务过程执行路径由一系列活动组成,其执行路径可看做一系列序列活动,所以未来的计划将研究扩展该模型,使其能够完成业务过程执行路径的预测.