基于自动机理论的密码匹配方法

姜克鑫， 赵亚慧， 崔荣一

(延边大学 工学院，吉林 延吉 133002)

0 引言

密码匹配问题实质上是字符串的匹配问题[1].传统的匹配算法主要有基于字符暴力匹配的BF算法[2-3]和通过消除主串指针回溯的KMP算法[4]，其中KMP算法的时间复杂度虽然低于BF算法，但KMP算法中因存在着相同字符的重复比较，因此其匹配效率仍相对较低.2019年，李先祥等[5]提出了BM算法.由于BM算法的速度比KMP算法快3～5倍，因此其受到学者的广泛关注.

1956年，Moore等首次提出了有限状态自动机的概念[6].随后，学者们利用有限状态自动机对字符串匹配的问题进行了研究.例如：文献[7]给出了一种高效的有限状态自动机的存储表示方法，并基于这种存储表示方法建立了一种效率高于KMP算法的模式匹配算法；文献[8]提出了一种基于自动机的多模式匹配算法(AC算法)，该算法在匹配失败时能够高效跳转，因此其匹配效率较好.但目前相关研究中所提出的自动机状态数目都是固定不变的，即仅能匹配特定的输入字符串，因此具有很大的局限性.为此，本文提出了一种新的有限自动机——状态数目可变自动机(variable number of states automata,VNS-DFA)，并通过算法分析验证了该自动机的有效性.

1 有限状态自动机

在自动机理论中，自动机都是指抽象的自动机，即是一种能变化和处理信息的离散动态数学模型.自动机可通过形式化语言、状态转移图以及状态转移表3种方式进行描述[9].目前，自动机主要包括确定型有限状态自动机、非确定型有限状态自动机、有穷概率自动机[10]、模糊有穷自动机[11]、下推自动机[12]、图灵机[13]等.其中确定型有限状态自动机是一种控制状态和符号集都有限的自动机，它能够对每个输入的字符做出识别，并保证所输入的字符串都能够到达最终的状态和路径[14].由于确定型有限状态自动机实现简单，且能应用于字符串匹配中，因此本文选用确定型有限状态自动机.

1)有限状态自动机.有限状态自动机M可表示为一个五元组的形式[15]：

M=(Q,Σ,δ,q0,F).

(1)

其中：Q为状态的非空有穷集合；q称为M的一个状态；Σ为输入字母表，输入字符串都是Σ上的字符串；δ为状态转移函数,δ∶Q×Σ→Q，对∀(q,a)∈Q×E,δ(q,a)=p，表示M在状态q时读入字母表的字符a，将状态q变成p，并处理下一个字符；q0为M的开始状态，q0∈Q;F为M的终止状态，F⊆Q.

假设公式(1)中的Q={q0,q1}，Σ={0,1}，q0为开始状态，F={q1}为终止状态，且δ(q0,0)=q0，δ(q0,1)=q1，δ(q1,0)=q0，δ(q1,1)=q1，此时自动机M的状态转移图如图1所示，其状态转移表如表1所示.在图1中，一个圆圈代表一个状态，带标签的箭弧表示转移函数，无标签的箭弧指向的圆圈表示初始状态，双圆圈表示终态.在表1中，表的各行对应M的状态，表的各列对应输入事件，其中有箭头标注的状态是初始状态，有*标注的状态是终态.

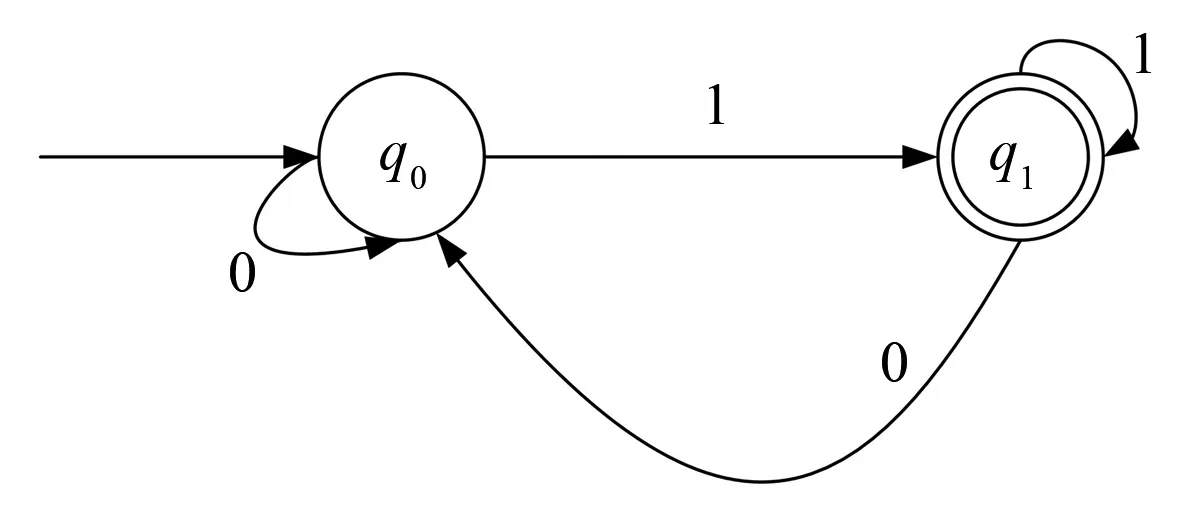
图1 M的状态转移图

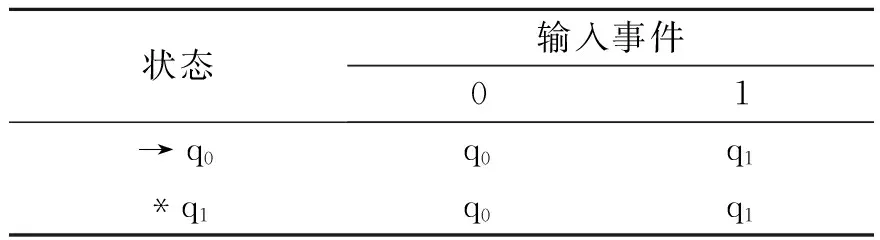
表1 M的状态转移表

由式(1)可知，上述定义的有限状态自动机M只能判别输入的字符串是否被自动机接受，但无法给出必要的中间结果和确定自动机M所接受的字符串是什么内容.对此，本文在公式(1)中增加了一个输出字母表Δ以及输出函数g∶Q→Δ，且当q∈Q时,g(q)=a表示M在q状态下输出a.

2)有限状态自动机接受的语言.自动机接受的所有字符串的集合称为自动机所接受的语言.设M=(Q,Σ,δ,q0,F)是一个自动机，对于∀x∈Σ*，如果δ(q0,x)∈F，则称x被M接受；如果δ(q0,x)∉F，则称x不被M接受.有限状态自动机所接受的语言可表示为：

L(M)={x|x∈Σ*且δ(q0,x)∈F}.

(2)

2 状态数目可变自动机(VNS-DFA)的构造

为提高用户密码的安全性，本文设计了如下用户注册和用户登录的流程：用户注册时首先设置密码，然后系统对密码进行同态映射加密;用户登录系统时，为防止密码被偷窥，将密码隐藏在所输入的字符串中.为了接受这些隐藏在字符串中的密码，本文构造了一种VNS-DFA自动机，只要用户输入的密码被该自动机正确识别即可成功登录.密码设置和VNS-DFA自动机识别的过程如图2所示.

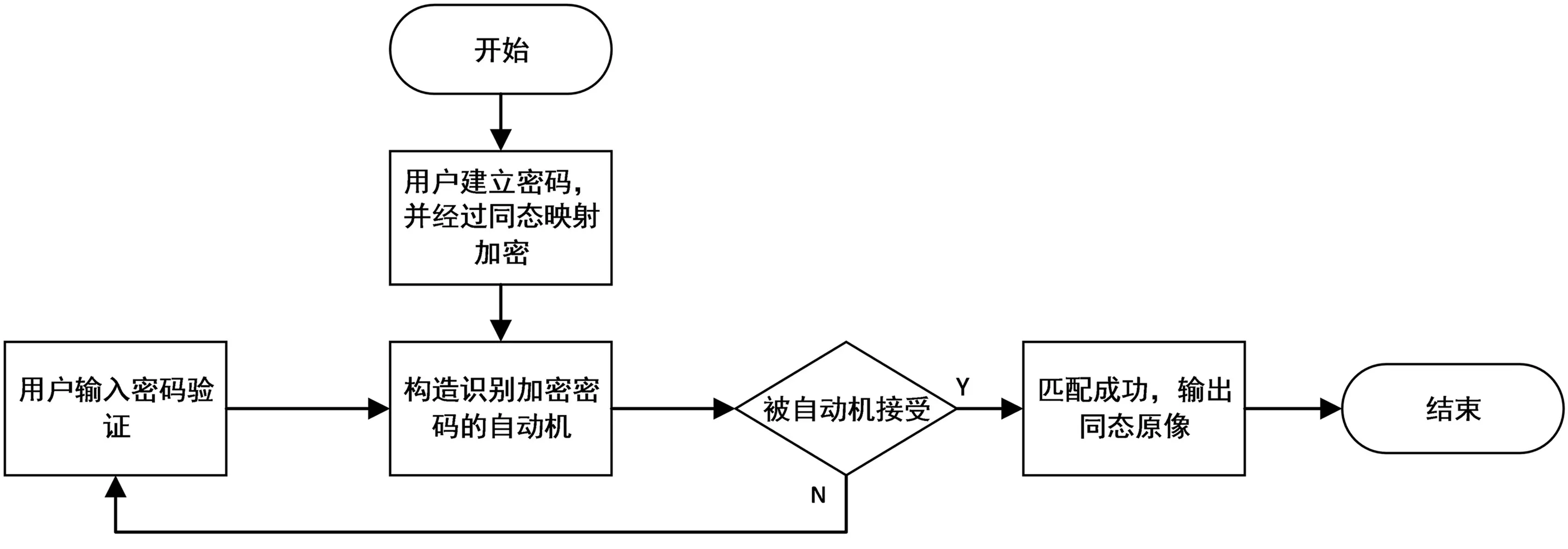
图2 密码设置和识别的过程

2.1 密码加密的过程

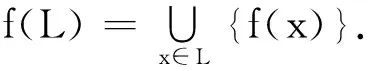
f-1(w)={x|f(x)=w且x∈Σ*}.

(3)

由式(3)可知，若w是经过加密之后的密码，则w的原始密码应包含在它的同态原像中.

2.2 自动机的构造及识别

本文设计的状态数目可变自动机(VNS-DFA)可用如下的七元组表示：

M=(Q,Σ,Δ,δ,q0,F,g).

(4)

其中：Q,δ,q0,F的含义与DFA中的含义相同；g为输出函数，∃q∈Q，a∈Σ,g(q)=a, 即在满足条件的状态q下输出原始字符a；Σ为输出字母表；Δ为Σ经过同态映射之后的输入字母表.

根据自动机的结构及原理，本文构造的VNS-DFA算法(算法1)的具体步骤如下所示：

输入：原始串s，验证串t.

输出：加密串在验证串中出现的次数.

Step 1 将串s进行加密，得到串s1.

Step 2 初始化自动机状态转移矩阵A，并对其元素全部赋值为0.

Step 3 修改矩阵A，其中m为s1的长度, 0为初态，n为终态.具体修改规则如下:

A[0][s1[0]]=1;

A[n][s1[0]]=n+1;

A[n+1][s1[1]]=2;

ifs1[0]= =s1[m-1];

A[n][s1[1]]=2;

A[i][s1[0]]=n+1,A[i][s1[i]]=i+1,i=1，…，m-1.

Step 4 初始状态k=0，匹配成功次数count=0，待匹配字符位置i=0.

Step 5 如果i= =n回到Step 6；否则,跳转至新的状态j=A[k][s1[i]]，并将j赋值给k;

ifj= =特定状态，输出相应数字,回到Step 5;

ifj= =n-1匹配成功，count+1，回到Step 5;

i=i+1.

Step 6 结束.

算法1中：输入是原始密码s和用户验证登录密码t，输出是t在s中是否出现及其出现的次数，矩阵A为自动机的状态转移矩阵，m为原始密码经过同态映射后的密码长度，0为初始状态，n为终止状态.

Step 3为算法1的核心.在由Step 3建立好的自动机中输入某个字符时，若自动机成功匹配，则跳转至下一状态，否则跳转至初始状态.Step 5为算法1的匹配过程，当且仅当状态跳转为终态时，输入的字符串才能被自动机所接受，同时输出其同态原像.

3 算法分析

3.1 算法的有效性证明

对于任意一个输入串a1a2…an，根据文献[16]中的定理1(对于任意的q∈Q,w∈Σ*,a∈Σ，都有δ(q,wa)=δ(δ(q,w),a))可以得到如下式子：

δ(0,a1a2…an)=δ(δ(0,a1a2…an-1),an)=δ(δ…(δ(0,a1)…),an).

(5)

根据算法1的转移规则(δ(0,a1)=1,…,δ(n-1,an)=n)，可将式(5)转变为：

δ(δ…(δ(0,a1)…),an)=δ(δ…(δ(1,a2)…),an)=δ(n-1,an)=n.

(6)

由式(6)可得

δ(0,a1a2…an)=δ(δ…(δ(1,a2)…),an)=δ(n-1,an)=n.

(7)

由式(7)可知，自动机在初态时可接受字符串a1a2…an，并且最后可到达终态.根据本文提出的算法所构造的识别串a1a2…an的有限状态自动机如图3所示.

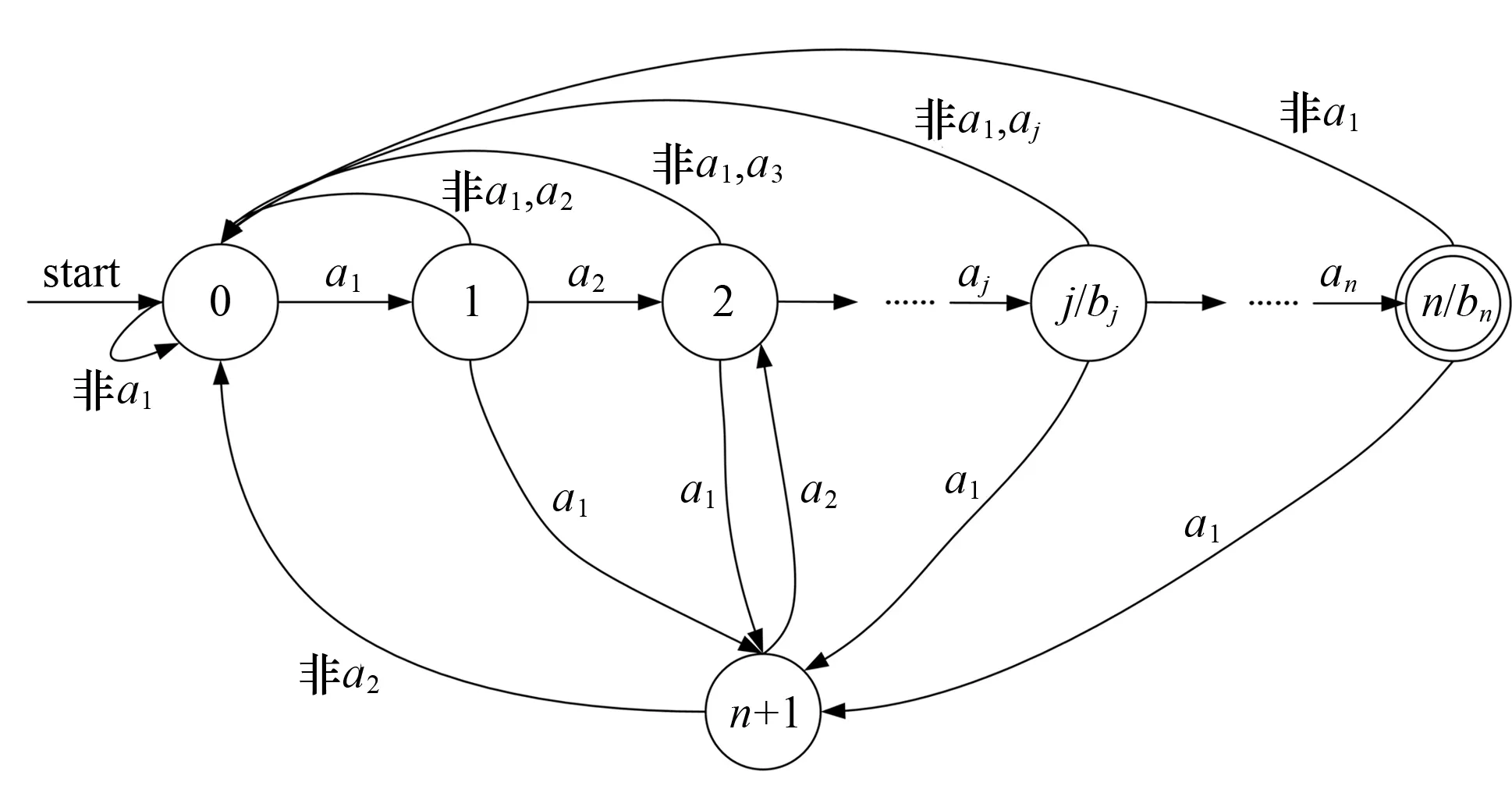
图3 识别a1a2…an的有限状态自动机

本文以输入密码s为例验证本文构造的自动机能够接受该密码.假设s= ′12′，且s对应的同态映射为f(1)= ′one′,f(2)= ′two′.在该假设下匹配该密码的自动机如图4所示.由图4可知：当输入的字符串中只要包含′onetwo′，该自动机就可接受该字符串；当自动机匹配到′one′时，自动机输出′one′对应的同态原像′1′；当自动机匹配到′two′时，自动机输出′onetwo′对应的同态原像′12′.由以上可知，本文提出的自动机能够匹配包含加密密码的字符串，并能够输出用户输入的原始密码，因此本文构造的自动机是有效的.

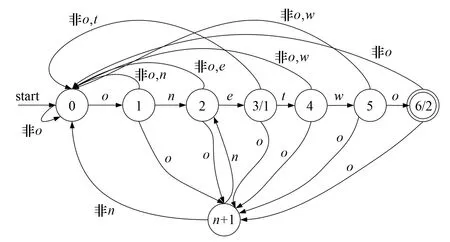
图4 识别原始串′12′的有限状态自动机

3.2 算法的复杂度分析

自动机算法的复杂度通常包括建立算法的时间复杂度和匹配字符的时间复杂度.为了验证VNS-DFA算法的有效性，本文将VNS-DFA算法的时间复杂度、空间复杂度与传统的DFA和改进后的DFA的时间复杂度、空间复杂度进行了对比，结果如表1所示.实验中，将待匹配串的长度设置为m, 输入串的长度设置为n, 字母长设置为|Δ|.

由表2可知：在时间复杂度上，在输入规模相同的情况下3种算法在字符匹配的过程中的时间复杂度均为Θ(n)，但VNS-DFA算法的建立时间最短(复杂度为O(m))；在空间复杂度上，在输入规模相同的情况下其差别不大.这是因为3种算法都可用二维数组表示状态转移矩阵，因此其大小取决于自动机的状态个数以及输入字母表的长度.

表2 3种不同算法的复杂度

4 结论

研究表明，本文构造的VNS-DFA能够匹配任意输入的字符串，且其匹配速率优于传统的DFA及改进的DFA，因此本文方法可以用于密码的识别.在本文的算法中，当待匹配的字符串长度较大时，会因自动机的状态数目增多而导致耗费更多的内存空间.因此在今后的研究中，我们将对自动机的状态数目进行改进，以节约内存空间.