修正评分的协同过滤算法
2020-01-14贾俊杰余钦科
贾俊杰,余钦科
1(西北师范大学 计算机科学与工程学院,兰州 730070)2(西北师范大学,兰州 730070)
1 引 言
随着互联网行业迈入大数据时代,网络为人们提供了海量的信息资源,极大程度地满足了用户对各类信息的需求.带来巨大便利的同时,网络信息过载问题也变得日益突出,用户在海量信息中找到自身所需信息的需求变得更为迫切.
在这样的背景下,信息推荐技术[1]作为信息过滤的有效手段,逐渐成为计算机学术和应用领域的热门研究对象,在互联网系统中被广泛地使用.推荐系统针对在用户没有明确的需求场景的情况下,通过采集用户历史信息和商品的特性,分析其中的关联特性,推测用户对潜在物品的个性化偏好情况,进而向用户推荐最优选择,帮助用户选择所需要的商品,在极大方便网站用户的同时,也有效提高了网站的运营效果和服务质量.
在众多推荐技术中,协同过滤算法[2]是当前应用较为成熟的一项技术.协同过滤算法认为有近似选择偏好的用户一般可能会喜欢相同的物品,具体可以分为基于用户的、基于项目的、基于模型的三类协同过滤算法[3].协同过滤算法的优点首先是能够过滤那些表达复杂的描述型内容,从而解决了难以进行自动内容分析信息过滤问题,另外还具有推荐新信息的功能.然而,协同过滤算法在数据量不断增大的情况下也有其问题和局限性,典型的就是评分矩阵稀疏性问题和冷启动问题[4]围绕这些问题,近年来学术界进行不断深入研究,提出了很多有效的改进方案.
本文为提高个性化推荐算法推荐过程的推荐精度以及改良协同过滤推荐算法矩阵稀疏性问题,选择用户聚类解决矩阵稀疏性问题.为了提高个性化推荐质量的目的下.本文算法先计算出聚类组中目标用户和其他用户之间的皮尔斯相关系数[1],设定阈值过滤掉弱相关的记录生成推荐组.当推荐组中用户再次发生购买行为,算法计算推荐组中目标用户与其他用户加权评分及置信度,用修正评分衡量推荐结果.经过实验,结果表明该方法可以提高推荐的精确度.
2 协同过滤算法
协同过滤算法根据用户-项目评分矩阵中已有的购买权重,利用用户间或项目间的相关关系预测评分矩阵中缺失的评分,然后根据评分的高低衡量用户对项目的偏好程度.其中最近邻查询的协同过滤算法是最基础部分,聚类查询是在最近邻查询的基础上采用聚类寻找最近邻来达到降低搜索空间,下面介绍最近邻查询和聚类查询.
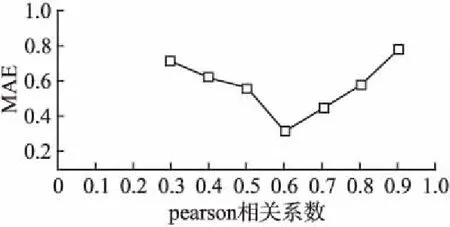
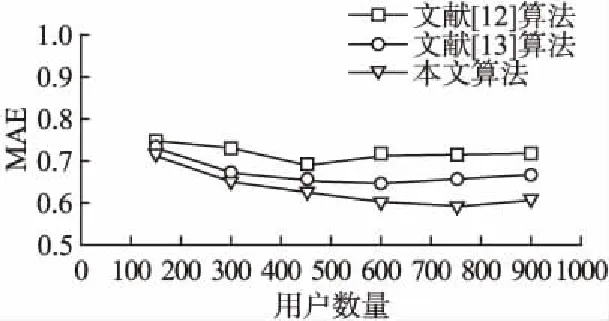
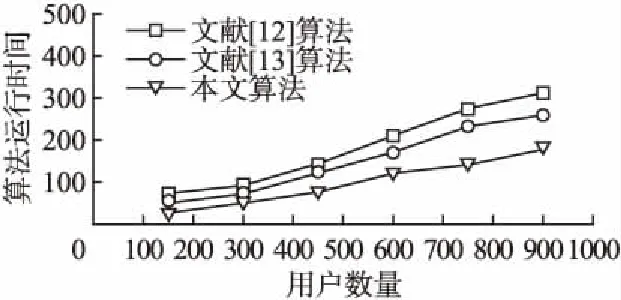
假设推荐系统中有m个用户,用户集合表示U{u1,u2,u3,…,um},购买商品集合表示为I{i1,i2,i3,…,in},用户—商品之间的权重矩阵为rm*n,rij(i 表1 用户-商品权重矩阵Table 1 User-commodity weight matrix 基于邻近关系的协同过滤推荐算法可分为基于用户的协同过滤(User-based CF,UCF)算法和基于项目的协同过滤(Item-based CF,ICF)算法[5].前者的基本思想是,从用户的行为和偏好中发现规律,并基于此给予推荐,相似的用户有相似的行为偏好,因此向目标用户推荐项目时,UCF算法查找与目标用户最相似的用户集,根据不同行为反映用户喜好的程度将它们进行加权,得到用户对于物品的总体喜好.为预测目标用户的偏好程度,首先要找到用户的相似邻居集,计算用户间相似度是协同过滤算法的关键.常用的相似性度量方法有余弦相似度[6]、Pearson 相关系数[7]和修正的余弦相似度[8].由于余弦相似度忽略了不同用户之间的不同评分标准,学者们又提出了修正的余弦相似度计算方法,将用户评分减去该用户的平均评分之后,再进行相似度的计算,计算方法如公式(1): (1) 再通过相似度计算得到目标用户的最近邻居集NN,通过公式(2)预测用户u对商品Ii的加权评分pu,i. (2) 根据上述方法预测目标用户u对未评分项目的评分,并选取评分的前N个项目,将其推荐给目标用户u. 传统基于邻近关系的协同算法在进行推荐时,在所有用户中查找与目标用户最相似的 k 个用户,算法的推荐效率随着系统用户数量的增加而降低,时间复杂度随之升高.为此Sarwar等人提出基于用户聚类的协同过滤算法[9],算法将推荐系统的中的所有用户划分为多个不相交的集合{Ui|∪Ui=U;∩=Ui=φ;i=1,2,…,l} 使得每个集合内用户的关联相似度尽可能高,而集合间的用户的相似度尽可能低.仅需在目标用户所属的集合中采用基于用户的协同过滤算法进行推荐,此举缩小了用户的查找范围,提高了推荐系统的效率,时间复杂度降低. 1)在用户数据量增大时,基于最近邻查询搜索空间巨大,时间复杂度增加,矩阵稀疏,影响推荐精度. 2)聚类查询降低了最近邻查询的时间复杂度,但同样遗留了推荐精度不足问题,传统算法考虑了用户与用户之间的关联,却忽略商品与商品关联,加权评分只考虑用户与用户间关联,导致推荐精度不够. 3)为保证推荐精度,推荐算法应考虑商品与商品的关联,本文引入关联规则中置信度概念.采用修正评分衡量推荐结果. 为解决传统推荐算法矩阵稀疏、推荐精度不足、用户异常值问题,本文提出结合聚类和关联规则协同过滤算法,采用修正评分代替加权评分衡量推荐结果.本文算法将用户-商品购买记录的商品权重作为原始数据,把整个推荐过程分为以下几个步骤: 1)数据预处理:对用户的商品数据字符重编码,并对应用户的商品权重. 2)用户聚类:利用k-means聚类对用户购买行为数据进行聚类,得到用户聚类组. 表2 预处理后的数据 用户品牌分类权重系数u1a1b2c4542u2a3b1c9321u3a3b1c9112u4a1b2c4515u5a7b5c6355u6a3b1c9314u7a1b2c4313u8a1b2c4241u9a7b5c6142u10a7b5c6453u11a1b2c4552u12a3b1c9345u13a3b1c9541u14a7b5c6122u15a1b2c4524 3)协同过滤,计算聚类组中目标用户和其他用户之间的相关系数,构建推荐组. 4)考虑商品—商品的关联,推荐组中计算目标用户对商品的加权评分以及商品—商品的置信度,用新的衡量指标:修正评分,对商品进行推荐. 5)产生推荐结果:对商品修正评分降序排列推荐给目标用户. 用户-商品数据按字符格式重编码,字母u组合不同数字表示不同用户.字母a、b、c表示商品不同类别,组合不同数字表示该类别下不同商品,预处理后数据如表2所示. 对用户-商品数据进行k-means[2]多维聚类,将用户分为不同的聚类组.表3为聚类后的数据集,预处理后的数据聚类为3个组,品牌分类有3列表示3个维度用a、b、c表示.聚类组如表3所示. 表3 用户聚类组 聚类组1用户品牌分类权重系数u1a1b2c4542u4a1b2c4515u7a1b2c4313u8a1b2c4241u11a1b2c4552u15a1b2c4524聚类组2用户品牌分类权重系数u2a3b1c9321u3a3b1c9112u6a3b1c9314u12a3b1c9345u13a3b1c9541聚类组3用户品牌分类权重系数u5a7b5c6355u9a7b5c6142u10a7b5c6453u14a7b5c6122 为对目标用户做推荐预测,需对聚类后用户更精细筛选构建推荐组.由此需对目标用户协同过滤找到用户的相似邻居集.用户间相似性的计算就成了协同过滤算法的关键之一.常用的相似性度量方法有余弦相似度、Pearson 相关系数和修正的余弦相似度.考虑到本文协同过滤需考虑用户-商品数据权值,本文采用Pearson 相关系数对用户协同过滤.皮尔斯相关系数如公式(3)所示: (3) 其中:ui和uj表示的是两个不同的用户,Sui,Suj是ui和uj的样品标准偏差.uii和uji表示用户ui和uj对商品ii的购买权重. 表3中聚类组1经协同过滤后所产生推荐组如表4所示. 表4 用户推荐组 用户品牌分类权重系数u1a1b2c4542u4a1b2c4515u8a1b2c4241u11a1b2c4552u15a1b2c4524 传统算法由于只考虑了用户间关联而忽略商品间关联,考虑到商品组间的关联,本文采用关联规则中的置信度来衡量推荐算法中商品之间的关联作用. I{i1,i2,i3,…,in}是一个项目集合.T{t1,t2,t3,…,tn} 是一个事务集合每一个事务是用户购买商品记录. 由于本文用户数据在经过聚类和协同过滤后,所构建的用户推荐组中出现以目标用户商品事务集频繁的频繁项集.例:目标用户商品事务集为T{t1,t2,t3,t4},推荐组中会出现事务集合为T{t1,t2,t3,t4}的频繁项集.所以本文不需要采用算法求取频繁项集. (4) 公式(4)中,mun(X)表示项目X的支持计数,数值为X在T出现的次数. 传统协同过滤算法采用加权评分对用户进行产品推荐,但加权评分没有考虑商品组间的关联,当推荐组中用户购买商品出现异常值,例如:用户u1购买商品a1权重特别大,即使推荐组中其他用户没有购买a1商品,也会使a1加权评分靠前,导致推荐.加权评分无法解决异常值问题,考虑上述问题,本文结合置信度和加权评分提出修正评分,当推荐组中个别用户再次出现某商品的异常值,该商品的置信度很小,置信度和加权评分的叠加使该商品修正评分靠后,不会被推荐.同时当推荐组中不存在异常值,加权评分相近,置信度修正推荐优先级.经实验验证修正评分可以更好的衡量推荐结果. 用户集合表示U{u1,u2,u3,…,um},用户商品集合表示为I{i1,i2,i3,…,in},用户商品权重集合R{r11,r12,r13,…,rmn}. 如矩阵I和R所示,I为用户—商品记录矩阵,0表示无购买记录,1表示有购买记录.R为用户—商品权值矩阵,数字表示购买权值. 定义2.修正评分:修正评分作为商品推荐最终指标,表示为推荐组中除目标用户外其他用户对某商品的加权评分乘以推荐组中该商品组间置信度.置信度基于商品记录矩阵I计算,表示某商品可能被购买的概率,衡量加权评分可信度.两者相乘为修正评分,公式为(5): (5) rec(ii)表示目标用户和推荐组中其他用户对商品ii的修正评分.p(ui,uj) 表示用户ui与uj的皮尔斯相关系数,ui为目标用户,uj为推荐组中其他用户,rji表示用户uj对商品ii的购买权重.X为不包含商品ii的商品集合,Y为X∪ii的商品集合.目标用户ui和商品ii无关联,ui是用户组中第i个用户,ii为商品组中第i件商品,如果用户ui购买商品组中第i件商品,对应权重则为rii,如表1所示. 产生推荐过程由表5所示. 表5 推荐结果 相关系数u1u4u8u11u150.8570.7090.9120.851商品权重a1b2c4d1e1u1552413推荐值d1e1基于聚类17.6913.47本文算法10.7112.04 表5中目标用户u15购买e1商品权重高于d1,基于聚类的协同过滤算法优先推荐d1,本文算法优先推荐e1,可看出本文算法中采用修正评分衡量推荐结果更优于基于聚类协同过滤算法采用加权评分衡量推荐结果. 本算法包括用户聚类、协同过滤、生成推荐三个步骤. 1)用户聚类 输入:用户集合U{u1,u2,u3,…,um}数据. 输出:用户聚类组U′ 、U″ 、U″′. 处理流程: a)用户-商品数据重编码,采用聚类算法进行聚类,得到不同的用户聚类组U′ 、U″ 、U″′. 2)协同过滤 输入:用户聚类组U′ 处理流程: a)确定皮尔斯相关系数p(ui,uj)阈值为p′. 3)生成推荐 输出:商品推荐序列I′{…ii…in…}. 处理流程: b)结合矩阵I和R计算目标用户ui和推荐组中其他用户对商品中I{i1,i2,i3,…,in} 可能被推荐商品的修正评分rec(…ii…in…). c)按修正评分rec(…ii…in…)降序排序得到商品推荐序列I′{…ii…in…}进行商品推荐. 为提高实验说服力,本文实验数据来自明尼苏达大学 GroupLens 研究小组通过MovieLens 网站收集的MovieLens100K 数据集[10],该数据集包含了 943 位用户对1682 部电影的 100000 条 1~5 的评分数据,每位用户至少对 20 部电影进行了评分.数据预处理后将数据随机分为两个部分,80%归为训练集,20%归为测试集. 实验采用平均绝对误差(Mean Absolute Error,MAE)[11]和时间复杂度两种评价指标来度量算法的推荐质量.MAE 是一种常用的用于衡量统计的准确性和比较的度量方法,能够准确地反应推荐质量的好坏.它用来衡量预测的用户偏好与实际用户偏好之间的误差,MAE 值越小,推荐准确度越高,假设系统预测的用户兴趣集合为(p1,p2,…,pn),用户的实际兴趣集合为(q1,q2,…,qn)计算方法如公式(6): (6) 时间复杂度是推荐系统为目标用户推荐其感兴趣项目所需要的时间,算法运营时间越短,时间复杂度越低,效果越好. 相关系数选择为测试目标用户与其他用户形成推荐组时,随相关系数阈值的不同,MAE值得变化.相关系数取值范围为0.3~0.9.实验如图1所示为MAE值随着皮尔逊相关系数的变化. 图1 MAE值随pearson相关系数变化Fig.1 MAE value varies with pearson correlation coefficient 图1描述MAE值的变化曲线,初始MAE值随pearson相关系数的增大而降低,当pearson相关系数为0.6时MAE值达到最小,随之增大,所以本文的pearson相关系数选择为0.6. 实验对比了在用户数量逐渐增加时,基于用户的协同过滤算法[12]和基于logistic用户特征[13]以及本文算法的平均绝对误差(MAE)值的变化,同时通过三种算法时间复杂度的比较来确定算法的优越性. 图2 不同用户数量下的MAE值的变化Fig.2 Changes in MAE values for different user numbers 图2描述了三种推荐算法随着用户数量的变化,MAE值的变化情况,三种算法都是随着用户数量的逐渐增加MAE值逐渐降低M至趋于稳定.由图知本文算法在MAE上优于上述两种算法. 图3 不同用户数量下的时间复杂度变化Fig.3 Time complexity changes under different user numbers 图3可知随着用户数量的逐渐增加三种推荐算法的运行时间也随之增加,当用户数量少三种算法的运行时间没有明显差距.当用户数量逐渐增加时本文算法在算法运行时间上优于上述两种算法. 综上实验结果表明,新算法相较文献[12]算法和文献[13]算法具有明显的优势,特别是样本的数量增大后新算法的绝对平均误差 MAE 值同等较小,时间复杂度同等较低. 推荐系统作为一个热门的研究领域,本文从降低数据维度和减少计算量以及推荐的准确性考虑,提出修正评分的协同过滤算法,算法先对用户聚类提高矩阵搜索空间效率,降低时间复杂度.修正评分代替加权评分解决异常值问题,提高推荐算法的准确性.该推荐算法因数据的特殊性,在数据预处理阶段需要按照本文要求处理数据并对原始数据重编码,降低推荐算法的计算量的同时也增加了预处理阶段的工作量.下一步考虑的是如何更好的对原始数据进行统一编码,减少预处理过程的计算量.
2.1 最近邻查询
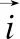
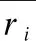
2.2 聚类查询
2.3 传统算法不足分析
3 修正评分的协同过滤算法
Table 2 Preprocessed data
3.1 数据预处理
3.2 聚类
Table 3 U ser cluster group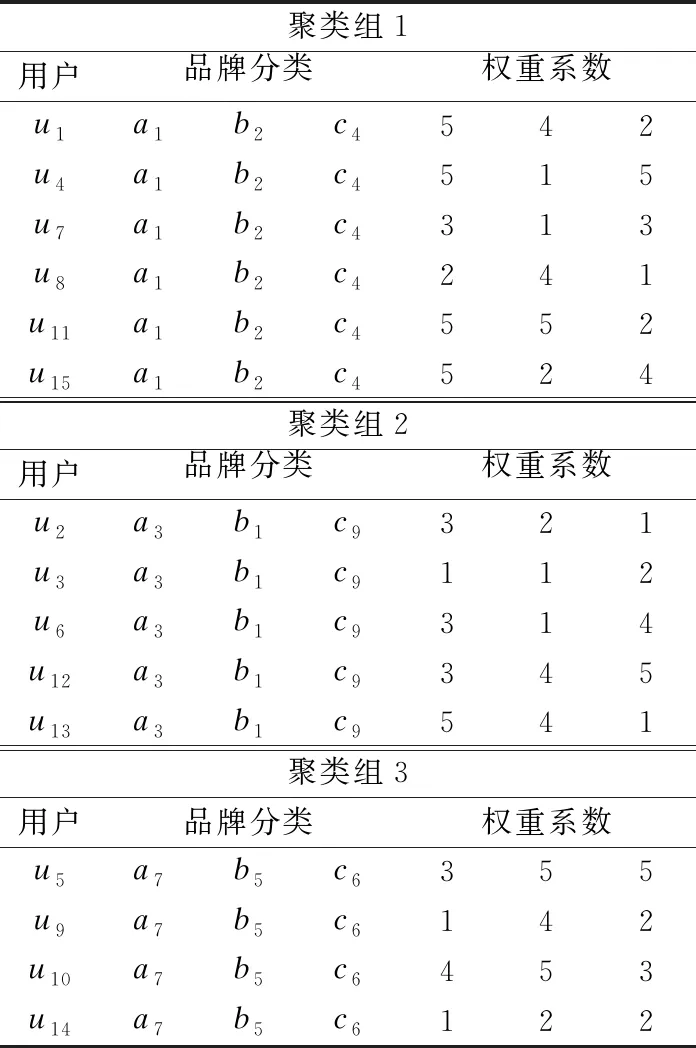
3.3 协同过滤
Table 4 User recommendation group
3.4 商品组间关联


3.5 修正评分
3.6 产生推荐
Table 5 Recommendation results
3.7 算法描述
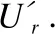
4 实验分析
5 结束语
