数学解题教学的微变革：英国方法融入中国课堂

林徐劢 黄兴丰

摘要：比较中英数学解题教学的特点可以发现，中国注重变式教学，英国注重“多学少教”。实践表明，变式教学有助于学生掌握解题方法，“多学少教”能够提升学生解题的灵活性、创造性。因此，以中国的变式教学为“脚手架”，融合英国的“多学少教”方法，可以得到一种很好的数学解题教学模式。

关键词：数学解题教学中英比较多学少教变式教学

一、英国的一则课例

笔者在随同上海数学教师团队赴英国访问期间，在伦敦一所女子中学相当于国内初二年級的一个学生水平较高的班级（英国中学实施的是分层走班教学），听了一堂统计图表课。课始，教师出示了这样一个富有挑战性的问题：

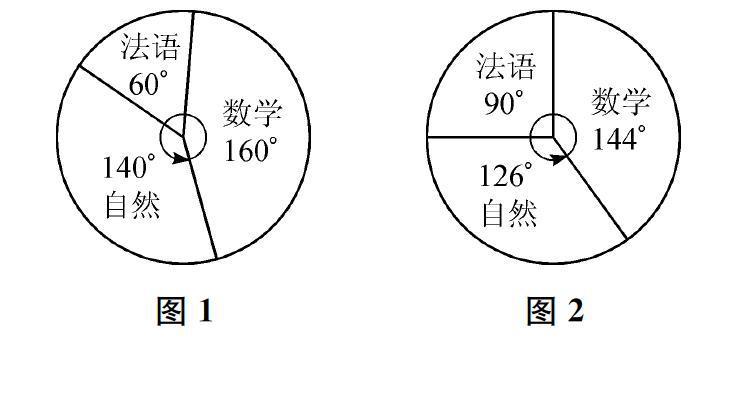
学校开设3门复习课，分别为法语、数学和自然。每位学生报1门复习课。第一周，学生的上课分布情况如图1。第二周，在原来基础上，又来了2位学生，都去了法语复习课，所有学生的上课分布情况如图2。共有多少位学生参加了数学复习课？

布置了这个问题之后，教师就开始了统计图表的教学，完全不管这个问题。直到课堂的最后几分钟，教师才回到这个问题，询问有没有学生想到解决的方法了。一位学生展示了自己用比例的方法解决这个问题的过程：原来的人数比是法语∶自然∶数学=60∶140∶160=3∶7∶8，现在的人数比是法语∶自然∶数学=90∶126∶144=5∶7∶8，故8位学生参加了数学复习课。

笔者没想到学生能想到如此新颖巧妙的解题方法，进而对教师抛出问题后让学生自主探究而不加任何引导的教学方式产生了极大的好奇。课后，笔者询问上课教师这样教学的意图是什么。

对方告诉我们：班级内有些学生具有浓厚的数学兴趣以及较强的数学能力，对于这节课的内容，可能不需要多少时间就可以掌握，因此，她在课始提出上述问题，希望这些学生在掌握了本节课基本的学习内容之余能够展开思考探究;至于不加任何引导，只是在课尾让学生展示解题过程，则是英国课堂解题教学常见的方式，背后的理念是希望学生通过独立思考和合作交流，自己找到解决问题的方法，从而充分体验“问题解决”的过程，学会“像数学家一样（无人指导地）思考”。

二、中国式“再设计”

对于上述问题的教学，中国的数学教师大多会这样设计：

考虑到上述问题主要涉及扇形圆心角与统计数据的关系等知识，难点在找到总人数或参加某门课的人数，要突破这个难点，需要找到等量关系列方程或算式，其方法比较多，教师可先带领学生复习扇形统计图相关的知识，再给出上述问题作为例题，然后通过师生问答的互动形式，引导学生分析题目，得到不同的解法。

此后，教师可基于上述问题（称为“原题”），改变数据（由“法语课+2”变为“数学课-6”），在不增加难度的情况下得到变式1;再增加变量（由“法语课+2”变为“法语课+1”“数学课+1”），在增加难度的情况下得到变式2。

变式1学校开设3门复习课，分别为法语、数学和自然。每位学生报1门复习课。第一周，学生的上课分布情况如图1。第二周，在原来基础上，6位上数学复习课的学生因为成绩进步不上了，所有学生的上课分布情况如图3。共有多少位学生参加了法语复习课？

变式2学校开设3门复习课，分别为法语、数学和自然。每位学生报1门复习课。第一周，学生的上课分布情况如图1。第二周，在原来基础上，又来了2位学生，一个去了法语复习课，另一个去了数学复习课，所有学生的上课分布情况如图4。共有多少位学生参加了自然复习课？

教学中，教师可先给出变式1作为练习，要求学生尝试解决，等到较多的学生得到正确答案后，组织学生讲解，酌情补充;再给出变式2作为练习，要求学生尝试解决，等到大多数学生得到正确答案后，组织学生分享。

三、中英两种教学方法的比较与融合

对于数学解题教学，英国教师在课堂上常常在课始抛给学生一道具有挑战性的问题，让学生独立思考或合作交流来解决，不给学生任何启发和引导，而在课尾让得到答案的学生展示讲解自己的解题过程，不做任何评价。

与此形成鲜明对比的是，中国教师在课堂上常常（尤其在学生遇到困难时）给学生很多启发和引导，帮助学生顺利解决问题，然后设计相关变式问题，促使学生迁移运用、反馈评价，帮助学生巩固提高（熟而生巧）。

比较两种教学方法，不难发现：

英国的教法突出了学生的主体地位，可能有益于发展学生的自主探究能力，激发学生的数学学习兴趣——J.S.Joseph指出，教师适当减少引导对学生的问题解决能力有正面的影响;又有一部分研究指出，教师应该让学生独立找到问题解决的方法并学会自己判断对错。但是，我们以为，这样的教学方法可能更适合“学优生”，而不利于“中等生”和“学困生”掌握解题方法，因而课堂效率相对较低——有时甚至花了整整一节课时间，还是没有学生真正解决问题。

而中国的教法通常突出了教师的主导作用，关注了全体学生，能够让大部分学生掌握解题方法，从而保证了学生的平均水平以及课堂的整体效率。同时，发挥了变式的作用，给学生提供了更多的学习空间——顾泠沅等人认为，数学活动中的过程性变式训练，可以帮助学生构建问题解决的方法，积累问题解决的经验，并从中总结出方法（经验）的多样性;变异理论甚至认为，学习源于变异。但是，这样的教学方法可能会使学生缺少自主探究的时间，缺乏个性化学习的机会，从而在主动性和创造性的发挥上有所欠缺。

由此，我们产生思考：能否将两种教学方法融合起来，发挥各自的优点，克服各自的缺点呢？于是，我们尝试将英国的“学生多学，教师少教”融入中国的变式教学，得到新的教学方法。

还是对于上述问题的教学，采用融合的教学方法，可以这样设计：

首先，教师直接给出原题，让学生独立思考或合作交流来解决，一段时间后让得到答案的学生展示讲解不同的解题方法。

其次，教师给出变式1，让学生独立思考或合作交流来解决，一段时间（应短些）后让得到答案的学生展示讲解不同的解题方法。

最后，教师给出变式2，考虑到课堂时间限制和学生学习情况，可让学生独立思考，一段时间（应更短些）后让得到答案的学生展示不同的解题方法。

四、教学效果的检验及启示

得到了三种教学方法后，我们尝试通过教学实践，检验它们的教学效果。

考虑到英国教法已经在一定程度上做了课堂教学实践，我们在上海一所初中七年级的两个平行班级，依据上述教学设计，分别对中国教法和融合教法进行课堂教学实践，得到学生解题的正确率、时间和方法数，数据如表1所示。

教法原题46.42%17.14%51534变式182.14%57.14%51024变式289.29%77.14%2514其中，采用中国教法的课堂上，学生解题的方法由以下的方法1、方法2、方法3三种最终统一为方法3一种;而采用融合教法的课堂上，学生解题的方法始终保持为以下四种。

方法1设第一周共有x位学生，则有方程x+24-x6=2，解得x=18，所以参加数学复习课的有160360×18=8（人）。或设第二周共有x位学生，则有方程x4-x-26=2，解得x=20，所以参加数学复习课的有144360×20=8（人）。

方法2设参加数学复习课的有x位学生，则有方程360144x-360160x=2，解得x=8。

方法3原来，法语∶自然∶数学=60∶140∶160=3∶7∶8，故设原来参加法语、自然、数学复习课的分别有3x、7x、8x位学生，则根据现在的比例，有方程3x+23x+2+7x+8x=90360，解得x=1，所以参加数学复习课的有8人。

方法4原来，法语∶自然∶数学=60∶140∶160=3∶7∶8，现在，法语∶自然∶数学=90∶126∶144=5∶7∶8。5-3=2，故参加数学复习课的有8人。

这里，方法1是间接设元列方程，方程很简单，很容易想到，最容易理解;方法2是直接設元列方程，方程稍复杂，很容易想到，较容易理解;而方法3是利用连比设元列方程，较难想到，也较难图5

理解;方法4是利用连比直接看出答案，含有方程思想，就是英国课堂上学生想到的方法，最难想到，也最难理解。

于是，比较上述教学效果，可以得到如下教学启示：

第一，变式教学有助于学生掌握解题方法。采用融合教法和中国教法的课堂上，随着变式教学的展开，学生解题的正确率都在增加，最终都超过了四分之三;时间都在减少，最终都比较熟练。反观采用英国教法的课堂，由于缺少变式教学，即使是让学生合作交流，学生解题的正确率也不会很高，时间也不会很短。可见，学生可以在有经验的问题上表现得比之前更好，变式练习构建了学生数学学习的“脚手架”，促进了学生对特定问题的理解与解决能力。此外，有关数据还表明，随着变式教学的展开，对于解题方法的掌握，“少学多教”只是短期效果较好，而“多学少教”的长期效果并不差。

第二，“多学少教”能够提升学生解题的灵活性、创造性。采用融合教法的课堂上，学生解题的方法一直较多;而采用英国教法的课堂上，即使只让学生独立思考，学生也想到了最难想到的方法。反观采用中国教法的课堂，由于实施“少学多教”，学生解题的方法则趋向单一、常规。可见，“多学少教”鼓励了学生的创新，促进了学生思维的发散。此外，有关数据还表明，实施“多学少教”时，对于解题的灵活性、创造性，变式与不变式的差异不大。

综上，以中国的变式教学为“脚手架”，融合英国的“多学少教”方法，可以得到一种很好的数学解题教学模式。这一教学模式可以用如图5所示的流程图来概括。

参考文献：

[1] J. S. Joseph. The Teaching of Science[M].Cambridge Mass：Harvard University Press，1964.

[2] 顾泠沅，黄荣金，费兰伦斯·马顿.变式教学：促进有效的数学学习的中国方式[J].云南教育（中学教师），2007（3）.

[3] 吴颖康，鲍建生.从上海经验看中国式数学课堂的典型特征[J].人民教育，2017（2）.

[4] 张奠宙，于波.数学教育的“中国道路”[M].上海：上海教育出版社，2013.

[5] 鲍建生，黄荣金，易凌峰，等.变式教学研究（再续）[J].数学教学，2003（3）.