“真”探索，“实”研究，数学思维自然生长——一道“探索研究”问题的教学启示

王翠玲

（江苏省睢宁县第二中学）

“探索研究”问题是苏科版《义务教育教科书·数学》（以下统称“教材”）在章节复习题中设置的题型，编写者旨在以此为契机，让学生通过探索活动，深化相应知识点，发展学生的思维.

但在实际教学中，笔者发现很多学生存在以下问题：（1）忽视解题切入点，解题路径、思路不够清晰，不能顺利解题；（2）缺少必要的解题反思，把解答原问题作为终结目标，学生“蜻蜓点水”式的假“探索”、虚“研究”，没有深入挖掘其内隐的思维精华，数学思维浅尝辄止，延展性不足.

本文以教材七年级上册的一道“探索研究”题为例，谈谈笔者的教学思考.

一、原题呈现与改编

题目（选自教材第6章复习题第14题）钟面角是时钟的时针与分针所成的角.

（1）举例说明，哪些时刻钟面角为30°，60°？

（2）举例说明，哪些时刻钟面角为90°？哪些时刻时钟的时针与分针重叠？

（3）与同桌合作：相互给出一些时刻，求出对应的钟面角的度数.

一般来说，问题的设置应遵循由易到难，由浅入深的逻辑顺序.相比较而言，第（3）小题较为简单，教师引导学生从此题入手，可以初步了解钟面角中基本的数量关系，为解决较为复杂的问题铺设台阶.基于此，笔者在执教时，对教材题目进行改编.

笔者通过基础性探索、拓展性探索与深层次探索等教学活动，引导学生认真探索与研究，以钟面角为契机，拾级而上，发展学生的数学思维.

二、教学过程简述

活动1：基础性探索.

问题1：钟面角是时钟的时针与分针所成的角.当1：00，2：00，3：00，12：00时，钟面角的度数分别为多少？

由于学生对整点时刻的钟面有较为丰富的生活经验，几乎都能给出每个整点时刻的钟面角度数.

（1）如图1，1点整（或11点整）的钟面角是30°.如图2，2点整（或10点整）的钟面角是60°.

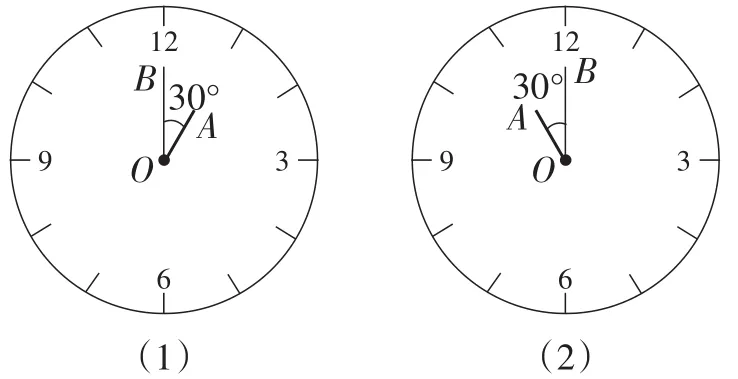
图1

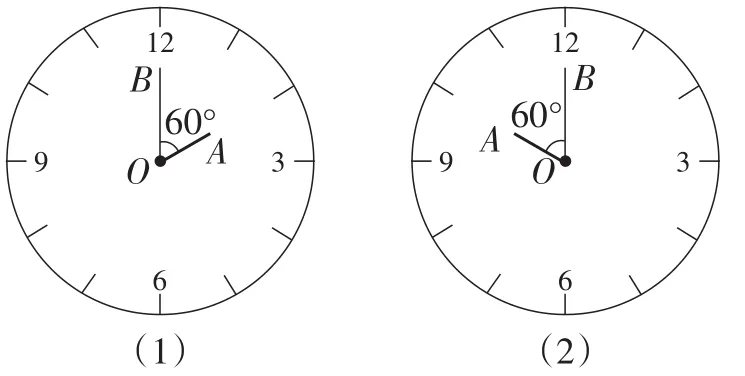
图2

（2）如图3，3点整（或9点整）的钟面角是90°.如图4，12点整的时针与分针重叠.

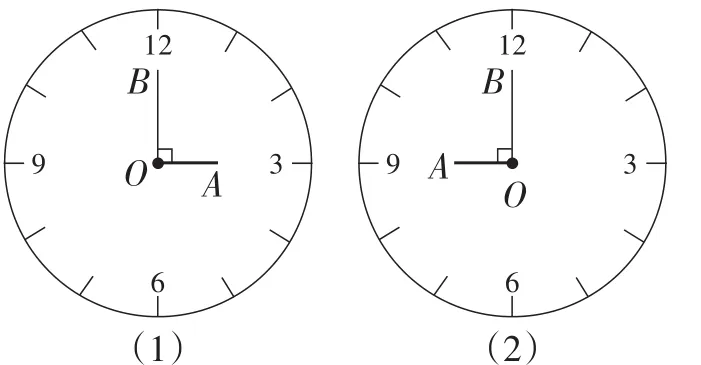
图3

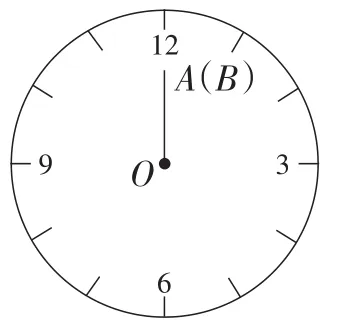
图4

此时，教师把握探索契机，通过设置以下问题串让学生明晰钟面角的基本算理，即时针与分针所成的几何图形可以看成角，并让学生结合钟面思考以下问题.

追问1：时针每小时旋转度数为多少？时针每分钟度数为多少？（时针每分钟旋转0.5°.）

追问2：分针每小时旋转度数为多少？分针每分钟旋转度数为多少？（分针每分钟旋转6°.）

【评析】整点时刻时的钟面角属于较简单的问题，设置该问题旨在让学生对分针、时针的旋转速度，以及它们之间的关系有初步的认识，感受钟面角的形成与时间之间的对应关系，为较复杂的探究活动奠定基石.另外，教师也可以让学生利用钟面角模型演示分针、时针的运行，形象感知它们的旋转速度之间的关系；对于某时刻的钟面角，可以利用钟面角模型或画示意图直接呈现，以便于学生探索钟面角的基本关系.

活动2：拓展性探索.

问题2：与同桌合作，相互给出一些时刻，求出对应的钟面角的度数.

对于问题2，部分学生在举例子时，受问题1的思维定势的影响，仍然会选择整点时刻进行探讨.此时教师可以因势利导，让学生列举出非整点的时刻，如当2：20时（如图5），钟面角的度数是多少？2：50呢？

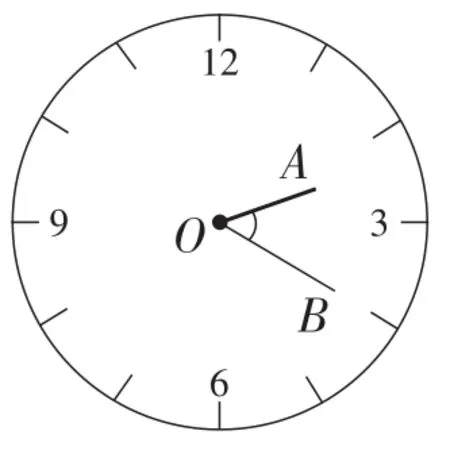
图5

首先，学生利用钟面角模型呈现如图5所示的图示，手脑协同解决问题.然后，教师引导学生思考：在相同时间内，时针与分针旋转的角度有什么关系？

以2：20为例，学生首先利用钟面模型摆出对应时间的时针与分针的位置.如图5，分针OB指向“4”，分针旋转了一圈的，即，而时针OA指向从“2”到“3”之间的处.根据从一个整点到下一个整点的旋转角是30°，教师引导学生进行钟面角的拆、补，利用角的和差关系，不难计算出此时的钟面角的度数.解决问题的方法如下.

图6

图7

【评析】从知识层面上看，拆、补是角的和差关系在生活中的应用.若辅助针的位置不同，拆、补的方法不同，和、差、倍、分关系也不同.通过探索活动，学生对角的和、差、倍、分关系一定有深刻的理解；从数学思想上看，拆、补蕴涵着转化的思想方法——将时间转化为角度，将“非整点”转化为“整点”，将不易求的问题转化为易求的问题.

探索活动应遵循由教师指导性的“半搀扶”，到让学生独立解决的“放手”的基本过程.例如，2：50时，钟面角的度数是多少？不妨让学生独立思考来解决问题.学生通过迁移以上解题经验，明晰探究路径.

（1）分针、时针究竟指向什么位置？

（2）钟面角如何转化？“辅助针”可以在什么位置？

（3）利用哪些角之间的数量关系求钟面角？

探索活动的主体是学生，教师应根据初中生年龄的特点和认知规律，遵循从易到难、从具体到抽象、从直接到间接的问题提出原则.相比较而言，“2：20”是“2：50”的脚手架，“2：50”又将是学生自编的其他时刻钟面角的脚手架.通过以上探索活动，使学生由浅入深地逐步探究，从而对角的内涵有更深刻的认识.

此时，该题的三个小题已经解决，探索研究活动是不是应该嘎然而止呢？No！笔者研究发现，钟面角问题蕴含着丰富的资源.学生通过深入探索，能够挖掘出更多有价值的知识，对学生数学思维的发展大有裨益.笔者现提供更为深入的探索研究活动（以下称之为“深层次探究”），与大家一起分享.

活动3：深层次探索.

此活动主要探究以下问题（问题3～问题6）.

问题3：举例说明，哪些时刻钟面角为90°？非整点时刻是否存在钟面角为90°？如时钟在1点多少分时，钟面角为90°？

对于“时钟在1点多少分时，钟面角为90°？”，学生很容易摆出时针的大致示意位置——时针指向“1”与“2”之间，而关键问题是分针在什么位置呢？学生通过摸索式实验，可以获得如下两种情况.情况1：如图8，分针在时针的右侧；情况2：如图9，分针在时针的左侧.

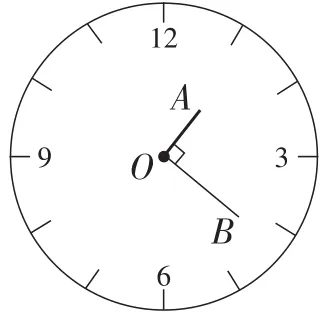
图8

图9

那么如何准确求出相应的时刻呢？仅仅利用现有的图示能解决问题吗？如图8和图9，在仅有一个孤立的角的情况下，不存在角与角之间的数量关系，不适宜直接计算，学生无从入手.

此时，教师可以让学生用辅助针（备用针）代替辅助线，鼓励学生尝试、探索，将其放在适当的、有价值的位置，借助辅助针与已知的时针、分针建立角与角之间的数量关系，列方程解决问题.

学生放置的辅助针的位置不同，辅助针与时针、分针所夹的角不同、数量关系不同，所列方程也不同，但均属于同解方程.

以情况1（分针在时针的右侧）为例.设1点x分（x＞0）的钟面角为90°，即∠AOB=90°，学生大致运用了以下方法解决问题.

方法1：如图10，设当辅助针OC指向“12”时，∠BOC表示分针x分钟所走的角度为6x°，∠AOC=0.5x°+30°.根据角之间的和差关系可得∠BOC-∠AOC=∠AOB.因此6x-(30+0.5x)=90.解得

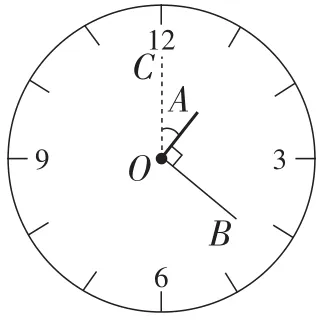
图10

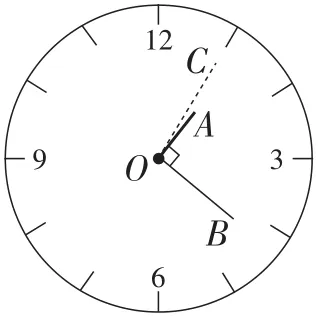
图11

方法2：如图11，当辅助针OC指向“1”时，∠BOC表示分针(x-5)分钟所走的角度6(x-5)°，即(6x-30)°.而∠AOC表示时针x分钟所走的角度0.5x°，根据角之间的和差关系可得∠BOC-∠AOC=∠AOB.因此(6x-30)-0.5x=90.解得

方法3：如图12，使用两根辅助针，即相当于添加两条辅助线.当辅助针OC指向“12”，辅助针OD指向“3”时，∠COD=90°，而钟面角∠AOB=90°，根据“同角的余角相等”，可得∠AOC=∠BOD.学生需要明确的是其中∠AOC=(30+0.5x)°，∠BOD可以看作分针(x-15)分钟所走的角度6(x-15)°，即(6x-90)°.所以30+0.5x=6x-90.解得

图12

图13

方法4：如图13，使用两根分别指向“12”“6”的辅助针OC，OD，相当于添加平角COD.由∠AOB=90°，可得∠AOC+∠BOD=90°.其中∠AOC=(30+0.5x)°，∠BOD可以看作分针(30-x)分钟所走的角度6(30-x)°，即(180-6x)°.所以列方程(30+0.5x)+(180-6x)=90.解得

类似地，当分针在时针的左侧时，学生根据以上探究经验，通过添加辅助线，构造角之间的和差关系，可以建立方程求解.方法如下.

如图14，当辅助针OC指向12时，有∠AOC=(30+0.5x)°，∠BOC=6(60-x)°.根据 ∠AOC+∠BOC=90°，列方程(30+0.5x)+6(60-x)=90，解得

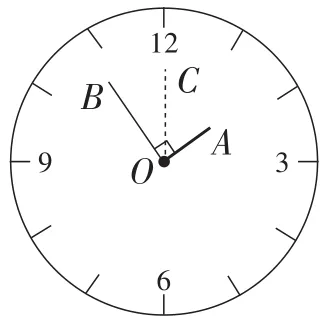
图14

同样，辅助线的位置不同，所列方程也不同.根据以上探究，学生可以获得结论：从1点到2点之间，有两个时刻的钟面角为90°，分别为1点分和1点

【评析】无论借用一根还是两根辅助针，其本质是添加辅助线，构造与“x分钟”相关联的角，即建立角之间的和差关系.在探究过程中，学生有不同的探索尝试，即将辅助针放在不同的位置，将有不同的解法.最初的探究中，学生要弄清楚时针、分针的大概位置，不可混淆，这是把握条件进行审题、解题的前提；最后教师应引导学生甄选优化方法，理解建立方程模型是解决问题的有效手段.

探究活动，是一种积累解题经验和解题方法的过程，教师应发挥主导作用，以帮助、提醒学生梳理、反思、优化解法，沉淀解题思想；同时，学生是探究活动的主体，教师应鼓励学生大胆思考、提出问题，并探究解决问题的方法.例如，在解决以上问题之后，学生不免猜想：从一个整点到下一个整点，90°的钟面角是不是都会出现两次呢？教师可以再次给学生提供“探索源”，即问题4.现笔者提供部分深层探究活动的教学片段，以便于研讨.

问题4：时钟在3点多少分时，钟面角为90°？这样的非整点时刻，90°的钟面角是不是也会出现两次呢？

生：也会出现两次.

师：我们利用钟面角模型摆一摆，或者动手画一画，算一算，验证一下.

生1：我画出了如图15和图16的两个图示，设3点x分的钟面角为90°（x＞0）.如图15，可列方程6x=0.5x.解得x=0.说明3点整时钟面角为90°；如图16，可列方程0.5x=6(x-30).解得说明3点分时的钟面角为90°.

图15

图16

生2：3点整属于整点时刻，不符合题目要求.也就是说，从3点到4点之间，90°的非整点钟面角会出现1次.

生3：非整点时刻说明x≠0，所以x=0应该舍去.

生4：在非整点时刻，x分钟时分针走的角为6x°，时针走的角为0.5x°，分针的速度大于时针的速度，所以在非整点时刻6x=0.5x不成立，其实图15是不存在的.

师：如果没有“非整点”限制，我们借助图15恰巧推算出3点整时钟面角为90°，所以积极探索常常会带来惊喜.那么，对于这个问题，能否不通过计算直接推测出“只会出现1次”呢？

生5：完全可以.我们可以把分针与时针当作绕着时钟的中心旋转、追及的两个物体.因为3点整时的钟面角恰巧是90°，从3点整到它们重叠，分针位于时针的左侧.因为分针走得快，时针走得慢，它们之间的夹角越来越小，则一定小于90°.所以从3点到4点之间，分针在时针的左侧时钟面角不可能是90°，而当分针在时针的右侧时钟面角会出现90°.

师：很精彩！时针与分针在旋转，或称之为追及的过程中，随着时间的推移，其夹角，也就是钟面角不断发生变化.大家继续探索思考问题5（不需要详细计算）.

问题5：12小时内，90°的钟面角会出现多少次？

生：……

学生通过操作、思考，可以获得结论：12小时内，90°的钟面角会出现24次（包括整点）.至此，学生已具备如下钟面角的探究经验：（1）作辅助线再构造角，根据“针”的旋转情况表示出相关角的大小；（2）根据角之间的数量关系直接计算或列方程，这是解题的关键！基于以上经验，学生能够顺利完成以下探索活动.

问题6：时钟在2点多少分时，时针与分针重叠（即钟面角为0°）？12小时内，时针与分针重叠多少次？

现分享学生的一种探究成果：设时钟在2点x分时，时针与分针重叠.如图17，∠AOD=6x°，∠AOC=0.5x°，∠COD=60°，根据∠AOD-∠AOC=∠COD（或根据“追及”问题的等量关系：相遇时，分针走的角度-时针走的角度=2点整时的钟面角），建立方程6x-0.5x=60.解得，即2点10分时，时针与分针重叠.

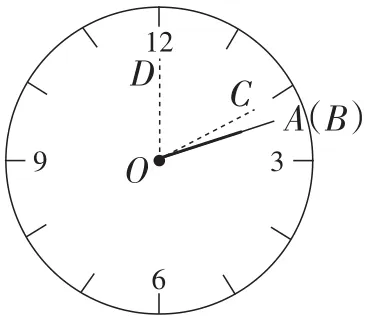
图17

对于钟面角问题，教师鼓励学生提出问题，深化思维，如在非整点的条件下，1点多少分钟面角为60°（或30°……）？哪些时刻的钟面角为180°？12小时内，钟面角180°会出现多少次？……

对于非整点的钟面角问题，学生可以按照如图18所示的四个阶段进行探索.

图18

“四个阶段”中，“突破阶段”是探索活动的重点，学生需要深入探索的是：由角度到钟面，即由“数”到“形”；再利用“数”解决问题，即由“形”到“数”.那么其中涉及了什么数学工具？利用什么数学模型来解决呢？这是钟面角问题的核心数学思想.

三、反思与启示

1.关于探索活动——求真务实

数学探索活动的方式具有多样性，以探索主体为分类标准，有自主探索，小组合作等方式；以探索媒介为标准，可以分为通过计算探索、利用图表探索、借助实验操作探索等.探索活动应求真务实，在获得解题方法的同时，真真切切地发展学生的数学思维.

（1）“真”探索的必要性.

探索活动是帮助学生理解、深化认知对数学知识的必要手段.在“钟面角”问题中，对于简单的问题，如“给出一些时刻，求出对应的钟面角”，学生有较为丰富的生活经验，能够根据钟面角的时针与分针的对应位置，直接求出钟面角的度数；反之，对于问题“给出一些钟面角，求出对应的时刻”，学生解决起来相对困难.教师可以引导学生通过探索活动“钟面角的实验演示”，来理解钟面角与时刻的对应关系，并提高学生解决问题的时效性.由角度求时刻，主要考查学生的逆向思维，这是学生思维的薄弱点.一般来说，学生除了对整点钟面角有可逆的认知以外，其他非整点的逆向认知经验相对不足，解题方法欠缺.因此，此时介入有真实体验的探索活动，是有必要的，也是有意义的.

（2）“实”研究的深刻性.

探索活动不是虚有其表的“摆摆弄弄”，是“看得见，摸得着”充分而深刻的思考方式.以探索活动之数学实验为例，其最大的优势是手脑并用，即有真实的触感，深刻的体验，理性的思辨.由角度求时刻，在非整点的情况下，如何求出符合条件的具体时刻？教师引导学生“真探索”——摆出钟面角.然后开展深入的探索研究，理解其合理性.思辨1：存在这种情况吗？怎样求出具体的时刻？思辨2：需要辅助针吗？此时，钟面角具有怎样的数量关系？思辨3：利用什么数学模型来解决？

数学实验是促进学生思考的载体，它是知识、经验与思维同步生长的有效方式，借助数学实验等探索活动，可以让学生在“数学好玩”的活动中顿悟，以使数学思维潜在生长.

探索活动往往以数学问题为原型，但教师不应止步于让学生解决数学问题，应从中引导学生探究数学问题指向的本质和算理，尽可能达到“解一类、通一片”的效果.例如，在“钟面角”问题中，通过对“时钟在1点多少分时，钟面角为90°？”等问题的探究，使学生深刻领会其中蕴涵的转化思想、方程建模思想、分类讨论思想等，自然能解决其他时刻钟面角为90°，0°，以及其他任意角度的问题.

2.关于数学思维——自然生长

解决问题不是探索活动的最终目标.探索活动应着眼于数学问题所蕴涵的数学思想，应关注数学思维的发展，使学生遗忘了所有知识之后，仍然留下的思维印痕.以本文的“探索研究”题为例，教师应关注学生数学思维的广度、深度等品质.

（1）关注思维的广度.

《义务教育数学课程标准（2011年版）》指出：学生应获得分析问题和解决问题的一些基本方法，体验解决问题方法的多样性，发展创新意识.多种解题方法的渗透能够拓宽学生的思维.因此，在教学中，教师要吃透教材、解透题目，引导学生从不同的视角，运用不同的解题工具和方法解题，并借机予以点拨，帮助学生积累解题方法和解题经验，以有效延展学生的思维.以前文“时钟在1点多少分时，钟面角为90°？”为例，教师鼓励学生多种方法放置辅助针——作辅助线，建立方程，能有效地开阔学生的数学思维.

（2）关注思维的深度.

对于一些蕴含丰富数学价值的思考题，笔者认为，教师应鼓励学生追问与深究，不能浅尝辄止.以“钟面角”问题为例，如果仅仅停留在教材预设的问题上，如果没有“非整点”的追问，如果没有n°的钟面角出现的次数的深究，那么“钟面角”就只是一道浅显的角度计算问题，其中隐藏的思维火种也将暗淡甚至熄灭.也就是说，思维深度首先来源于对问题的挖掘，其次，反思解题思想方法能使数学思维得以沉淀和升华.

（3）关注思维的严谨性.

数学是一门严谨的科学，其思维也具有严谨性.因此教师应关注学生思维参与的全过程.一方面，关注审题过程，培养学生独立思考、严谨审题的能力，使学生逐步学会抓住关键词、弄清楚确定因素、讨论不确定因素等；另一方面，关注解题过程，培养学生利用已有的数学工具严谨、灵活解题的能力，使学生逐渐形成合理验证、解决问题的意识.

数学是思维的体操.无论什么题型，都可以看作外显的思维形式，学生只有经历真真切切的探索，实实在在的研究，才能汲取内隐的思维精华，使数学思维自然生长.