lp-值Wiener过程增量在Hölder范数下的局部Strassen重对数律

刘永宏,刘海国,周霞

(桂林电子科技大学数学与计算科学学院,广西高校数据分析与计算重点实验室,广西 桂林541004)

1.引言与主要结果

Wiener过程及其增量的极限定理是一个广泛研究的话题,已有许多深刻结果.危启才在文[3-4]中研究了lp-值Wiener过程在Hölder范数下的泛函极限问题.对局部情形的极限定理人们也有研究,例如Gantert[1]研究了Brown运动局部Strassen重对数律,高付清等[2]研究了Brown运动增量的局部泛函极限定理.本文我们研究了lp-值Brown运动增量在Hölder范数下的局部Strassen 重对数律,文[3-4]中的有关结果可作为本文结果的推论.

设 {W(t);t ≥0}={Wk(t);t ≥0}是一列独立的Wiener过程序列,e={ek}是一列实数序列.记序列 {ekWk(t);t ≥0}为 {e·W(t);t ≥0}(简记为e·W).对p ≥1,记

为了叙述我们的结果,需要引入如下概念.

定义如果下列条件满足,则称(X,B,j,µ)为一抽象Wiener空间

(a)X是一实可分的Banach空间;

(b)B是一实可分的Hilbert空间;

(c)j:B→X是连续线性映射,且j(B)在X中稠密;

(d)µ是(X,B(X))上的概率测度,满足：对任意x′ ∈ X′,有其中X′是X的共轭空间,表示X与X′之间的二元关系,j∗:X′→B′=B是j的伴随算子.

易知

设(1.2)式成立.记C0[0,1]为所有满足e·f(0)=0的连续函数向量e·f=(e1f1,e2f2,···):[0,1]→R∞组成的集合.在空间C0[0,1]上,赋予Hölder范数||·||lp,α,记[0,1]为C0[0,1]中所有满足的向量e·f组成的子空间.易知,[0,1]关于Hölder范数||·||lp,α构成一可分的Banach空间.因此,由文[3]中定理A可将e·W看作一在Cp,α0 [0,1]中取值的随机变量.

现在设(1.2)式关于p=2成立.设

那么H关于如下内积构成Hilbert空间,

设j为[0,1]的自然嵌入映射,P为l2-值Wiener过程在([0,1],B([0,1]))上生成的概率测度.由文[3]中的讨论,l2-值Wiener过程可看成是抽象Wiener空间([0,1],H,j,P)上的随机变量.

定义映射I:[0,1]→[0,∞]如下

记K= {f=(f1,f2,···);f绝对连续,

全文中,设au,bu是两个从(0,1)到(0,e−1)非减连续函数,满足

(i)au ≤bu,u ∈(0,1),并且

对u ∈(0,1),0≤t ≤bu−au,∆(t,u)记下面轨道:

设

本文的主要结果陈述如下:

定理1.1如果条件(i)和(ii)被满足,那么以概率1,{βue ·∆(t,u);u ∈(0,1)}(u→0)在[0,1]中相对紧,且其极限点集是e·K.即,

且

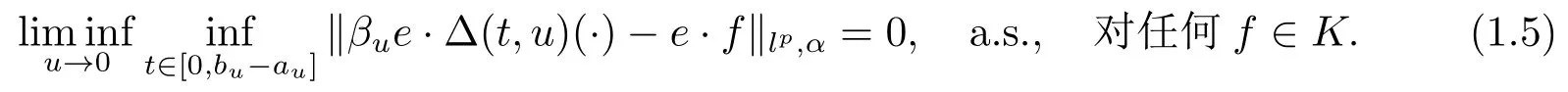
如果条件

也成立,那么,我们有

2.大偏差公式

引理2.1[4]设(X,B,j,µ)是抽象Wiener空间,则对任何Borel集E ⊂X,我们有

其中Λ(E)=inff∈E Λ(f).Λ:X→[0,∞]定义如下

引理2.2设(1.2)成立,p=2.则对任意闭集F ⊂C20,α[0,1],我们有

其中I(F)=inff∈F I(f),0

证参看文[4]中引理3的证明.

3.定理1.1的证明

我们证明定理1.1需要分三种情形:(I)p=2,(II)1≤p<2,(III)2

情形(II)和(III)的证明分别参看文[4]中定理1证明的Case II和Case III.

下面给出引理,证明当p=2时定理1.1成立.

引理3.1存在非增序列 {un ∈(0,1),n ∈N} 满足limn→∞un→0,使得对任何ε>0,

{un}在后面证明中分情形定义.

证设A= {[0,1]:||φ−e·K||l2,α ≥ε}.显然,A是闭集,I(A)>故存在充分小δ >0,使由引理2.2,当n充分大时,我们有

我们讨论如下：

由(3.1),(3.2)和Borel-Cantelli引理,我们得到

引理3.2如果条件(i)和(ii)成立,那么我们有

证设

则

我们得到

又由文[4]中(3.6)的证明,存在常数c>0,有

为完成本引理证明,我们分情形讨论：

由引理3.1,故(3.3)获证.

由引理3.2,当p=2时,(1.4)获证.

引理3.3如果条件(i),(ii)成立,则对任何f ∈K,我们有

证设u1=1,并且ρ=

若ρ <1且bu→b≠0,(u→0),那么在这种情形由下面引理3.5可得到(1.5).故此处只考虑两种情形：1)ρ<1且bu→0,(u→0); 2)ρ=1.情形1)若ρ<1且bu→0,(u→0).我们选uk使得

对任意ε>0,由scaling性,我们有

其中A= {e·g;||e·g−e·f||l2,α <ε}.因为e·K为紧集,故只需证明,对g ∈K,当2I(e·g)<1时,结论成立即可.若2 infe·g∈A I(e·g)<1,则可选η >0,使σ′=2 infe·g∈A I(e·g)+η <1.由引理2.1(大偏差),当k足够大时,

存在常数k0≥1,c>0,使得

因此,

因为 {||βune·∆(bun−aun,un)−e·f||l2,α ≤ε}独立(n ≥1),由Borel-Cantelli引理得到

情形2)ρ=1.若ρ=1,则au=bu,在这种情形参看文[3]中定理2.

由引理3.3,当p=2时,(1.5)获证.

引理3.4如果条件(i),(ii)和(iii)皆成立,则对任何f ∈K,我们有

证由于故存在递减子列 {un;n ≥1}使设ti=iaun,i=且h(n)则且h(n)→∞,(n→∞).而且,对任何小的我们得到

其中A= {g;||g−e·f||l2,α <ε}.若则可选δ >0,使µ=由引理2.1(大偏差),对n足够大

选适当的p,使由Borel-Cantelli引理

引理3.5假设条件(i),(ii)和(iii)皆成立,对f ∈K,设ϕt,u(s)=βue ·(W(t+aus)−W(t)),s ∈[0,1],t ∈[0,bu−au].若

则

其中aun,bun如引理3.4定义.

证因为我们有

又由文[4]中(3.6)的证明,存在常数c>0,有

注意到

故引理3.5获证.

由引理3.5,当p=2时,(1.6)获证.从而对p=2情形,定理1.1获证.