Existence and Uniqueness of Mild Solutions for Nonlinear Fractional Integro-Differential Evolution Equations
2020-01-10HOUMimi侯咪咪XIXuanxuan西宣宣ZHOUXianfeng周先锋
HOU Mimi(侯咪咪),XI Xuanxuan(西宣宣),ZHOU Xianfeng(周先锋)
(School of Mathematical Science,Anhui University,Hefei 230601,China)
Abstract: In this paper,we will study a class of nonlinear fractional integro-differential evolution equations in a Banach space X. We use the fractional power of operators and the theory of analytic semigroups to prove the existence and uniqueness of the solution for the given problem.Furthermore,we give the Hölder continuity of the obtained mild solution.
Key words: Analytic semigroup; Mild solution; Existence and uniqueness; Hölder continuity
1.Introduction
Fractional differential equations have been applied in many fields,including electrochemistry,control,quantum mechanics,biological systems,porous media and electrodynamics.There has been a significant development in fractional differential equations in recent years.[1−5]
Evolution equations are abstract differential equations in Banach spaces and are generalizations of concrete equations.Theory of evolution equations have lots of applications in partial differential equations.Theory of semigroups play an important role in evolution equations.Recently,there has been a rapid development in fractional evolution equations.[6−12]
In this paper,we consider the following nonlinear fractional integro-differential equation

Regarding earlier works on the problems of existence and uniqueness for nonlinear fractional differential equations.[13−17]Dhage et al.[17]has studied the equation with form as follows:
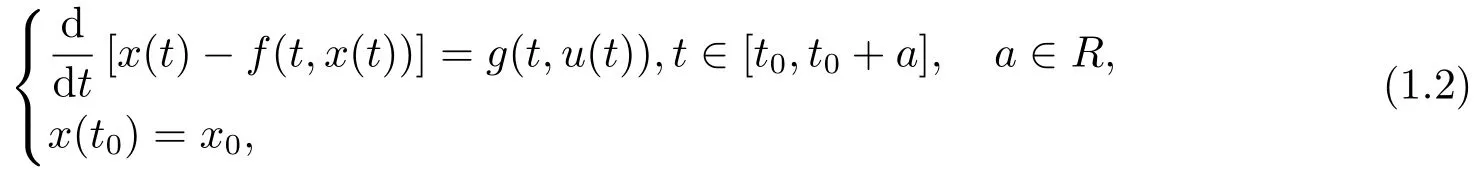
wherex(t)∈C(J,R),f ∈C(J ×R,R),g:J ×R→R,which is a Lebesgue integrable function.It is worthy to mention that the equation is not abstract.Pandey et al.[18]has considered the existence and uniqueness of the following fractional integro-differential equation

in a Banach spaceE,whereAgenerates an analytic semigroup.The authors used the theories of the semigroup and fixed point theorem to prove the existence and uniqueness of the solution.
Our investigation is motivated by the work of Dhage et al.[17]and Pandey et al.[18]The authors in [18]have discussed the existence and uniqueness of Eq.(1.3).In the present work,we use some of the ideas of Kumar et al.[19]and Musilm[20]to obtain the results of existence and uniqueness.Our calculation is different from [19-20].
In this paper,we will study the existence and uniqueness of mild solution of Eq.(1.1)by using the fixed point theorem and theories of analytic semigroup.Furthermore we prove the Hölder continuity of the obtained mild solution for Eq.(1.1).The rest of paper is organized as follows.In Section 2,we give some useful preliminaries about the fractional differential equations.In Section 3,we give our main theorem and its proof.In Section 4,we give the Hölder continuity of the obtained mild solution for Eq.(1.1).
2.Preliminaries
In this section,we introduce some definitions and preliminary facts which we will used throughout this paper.We observe that if−Ais the infinitesimal generator of an analytic semigroupS(t),t ≥0,then−(A+ϱI)is invertible and generates a bounded analytic semigroup forϱ>0 large enough.Thus we can reduce the general case in which−Ais the infinitesimal generator of an analytic semigroup to the case in which the semigroup is bounded and the generator is invertible.Hence without loss of generality,we suppose that

and

whereρ(−A)is the resolvent of−A.The fractional powerA−qis defined by
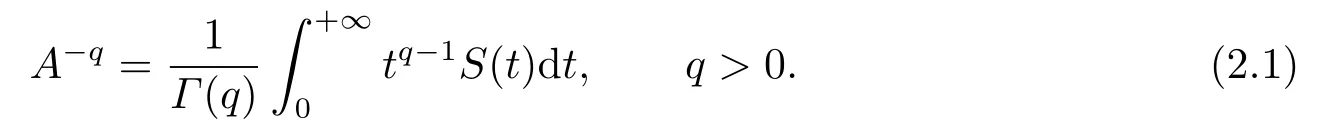
Aqis the invertible operator ofA−q.It follows that for 0< q ≤1,Aqis a closed linear invertible operator.Its domainD(Aq)is dense inXandD(Aq)⊃D(A).The closeness ofAqmeans thatAq,endowed with the graph norm ofAq,|||u|||=||u||+||Aqu||,u ∈D(Aq),is a Banach space.SinceAqis invertible,its graph norm|||·|||is equivalent to the norm||u||q=||Aqu||.Thus,D(Aq)equipped with the norm||·||qis a Banach space which we denote byXq.Whenq=1,we denoteD(A)byX1with norm||Au||=||u||1.About more details,one can refer to [21].
Definition 2.1[2,4−5]The Rieman-Liouville fractional integral operator of orderα ≥0,of a integrable functionfwith the lower limit 0,is defined as follows:

The Riemann-Liouville derivative has certain disadvantages when trying to model real world phenomena with fractional differential equations.Therefore,we will introduce a modified fractional differential operatorcDαproposed by M.Caputo.
Definition 2.2[2,4−5]The M.Caputo derivative of orderαwith the lower limit 0 for a functionfcan be written as

where the functionf(t)has absolutely continuous derivatives up to ordern−1.
Remark 2.1Iffis an abstract function with values inX,the integral which appear in Definitions (2.1)and (2.2)are taken in Bocher’s sense.Integrating both sides of Eq.(1.1),we have

For more details,one can refer to [8].
By using the method of Lemma 3.1 of [9],we obtain the following lemma.
Lemma 2.1If Eq.(2.3)holds,then we have

whereζα(θ)is a probability density function defined on (0,+∞),that is

and

Its Laplace transform is given by

Lemma 2.2[19,21]Let−Abe the infinitesimal generator of an analytic semigroupS(t).If 0∈ρ(A),then
(a)S(t):X→D(Aq)for everyt>0 andq ≥0;
(b)S(t)Aqu=AqS(t)ufor everyu ∈D(Aq);
(c)The operatorAqS(t)is bounded and||AqS(t)||≤Cqt−q,t>0.
Lemma 2.3[21]Let−Abe the infinitesimal generator of an analytic semigroup,then
(a)Aαis a close operator with domainD(Aα)=R(A−α)=the range ofA−α;
(b)0<β ≤αimpliesD(Aα)⊂D(Aβ);
(d)Ifα,βare real thenAα+βx=AαAβx.
We use the similar calculation presented in Theorem 3.2 of [22]to find the upper bound of integral,thus we get the following lemma.
Lemma 2.4For any 0≤t′ where 0<δ <1,c=1− ProofIt is easy to see that SettingR(t)=we can write wheret′ Before we give our main result,we first state the following definition. Definition 3.1The local mild solution of Eq.(1.1)onJmeans that a continuous functionudefined fromJintoXwhich satisfies the following integral equation: Remark 3.1Ais the infinitesimal generator of an analytic semigroup,andA−qis defined by(2.1),hence||Aq−1||is bounded for 0 Theorem 3.1Suppose that the operator−Agenerates the analytic semigroupS(t)with||S(t)||≤M,t ≥0,0∈ρ(A),and the following assumptions hold: (H1)LetDbe an open subset ofJ ×X1,f:D→X1satisfy the conditions:for every(t,u)∈D,there is a neighborhoodVof (t,u)(V ⊂D)and the constantsL,vandHsatisfyingand 0<ν ≤1,such that for all (ti,ui)∈V,i=1,2,where we denoteD(A)byX1. (H2)For an open subsetEofJ ×Xq,h:E→X,g:E→Xsatisfy the conditions:For every (t,u)∈E,there is a neighborhoodUof (t,u)(U ⊂E)and the constantsL1,L2andνsatisfyingL1>0,L2>0 and 0<ν ≤1,such that for all (ti,ui)∈U,i=1,2,whereXis a Banach space,and we denoteD(Aq)byXq. Suppose further that the real valued mapais integrable onJ.Then Eq.(1.1)has a unique local mild solution for everyu0∈X1. ProofChooset∗>0 andr >0 such that the estimates (3.2),(3.3)and (3.4)hold on the sets By the inequalities (3.2),(3.3)and (3.4),there exist positive constantsB,B1andB2such that ChooseTsuch that for 0≤t ≤T, for a givenθ ∈[0,+∞),and whereCqis a positive constant depended onqsatisfying ForT >0,denote L etY=C([0,T];X)with usual supremum normWe define a map onYbyFywith the following form for everyy ∈Y,t>0,whereFy(0)=Aq[u0−f(0,u0)]+Aqf(0,u0)=Aqu0. LetGbe the nonempty closed and bounded subset ofYdefined by We first prove that the mapFis fromGintoG.For anyy ∈G,we have by (2.5)that where By (3.7),we have By (2.6),(3.9)and the assumption (H1),we have that We have by (2.6),(3.3)and (3.9)that We get by (2.6),(3.4),(3.9)and (3.10)that By (3.8),(3.14),(3.15),(3.16)and (3.17),we get that Therefore,FmapsGinto itself.Moreover,for anyy1,y2∈G,we have where According to the assumption (H1)and Lemma 2.3 (d),we get We have by (2.6),(3.9)and the assumption (H1)that One can derive by (2.6),(3.9)and the assumption (H2)that By (2.6),(3.9),(3.10)and the assumption (H2),we get Therefore,we have by (3.20),(3.21),(3.22)and (3.23)that Letu=A−qy(t),then fort ∈[0,T],we obtain by (3.25)that Thusuis a unique local mild solution to Eq.(1.1).The proof is complete. In this section,we give the proof of the Hölder continuity of the solution of Eq.(1.1). Theorem 4.1Assume that the assumptions(H1)and(H2)hold.Then the mild solutionu(t)of Eq.(1.1)is Hölder continuous. ProofBy the previous arguments in Theorem 3.1,there exists a positive numberT0such that Eq.(1.1)has a unique mild solution on the intervalJ0=[0,T0]given by Letv(t)=Aqu(t),we have by Lemma 2.2(b)that For convenience,set Then (4.2)can be rewritten as Since the mapsf,gandhsatisfy the assumptions (H1)and (H2),u(t)is continuous onJ0,we can let Next,we have where Now,we calculateK1.For eachx ∈X1,we can write Hence,we get that Furthermore,we get by (2.6),(3.9),Lemma 2.2(b)and Lemma 2.3(d)that By Lemma 2.3 (d)and the assumption (H1),we have We get by (2.6),(3.9)and (4.4)that We obtain by (2.6),(3.9)and (4.4)that whereλ1=1−αq,µ1=andαq≠1.By Lemma 2.4,we have Furthermore,we have By the boundness ofA−qand (4.14),u(t)is Hölder continuous.The proof is complete.
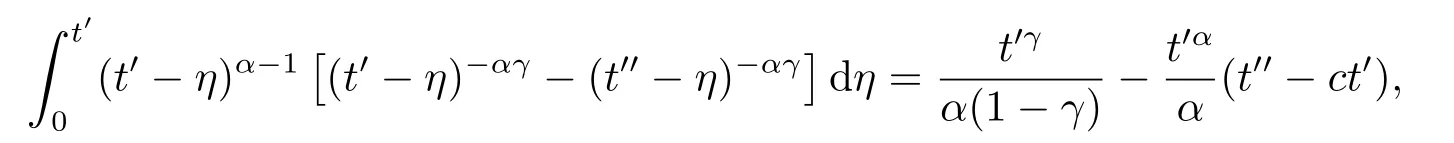
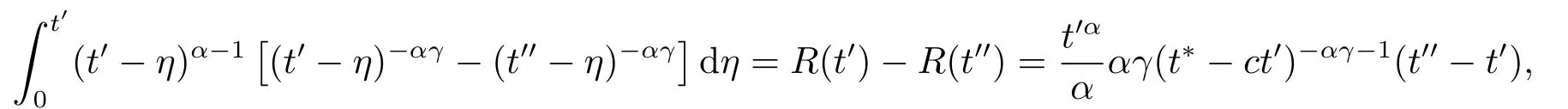

3.Local Existence of Mild Solutions

max {1,||Aq−1||}.














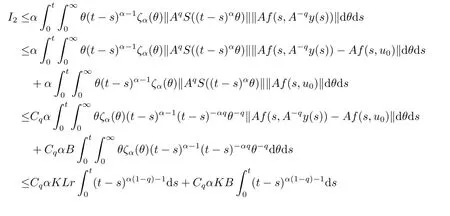

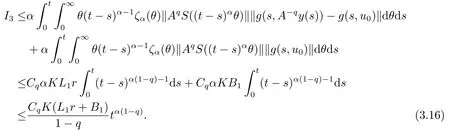












4.Hölder Continuous


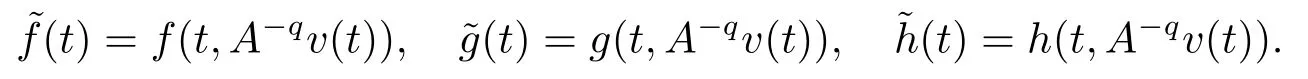

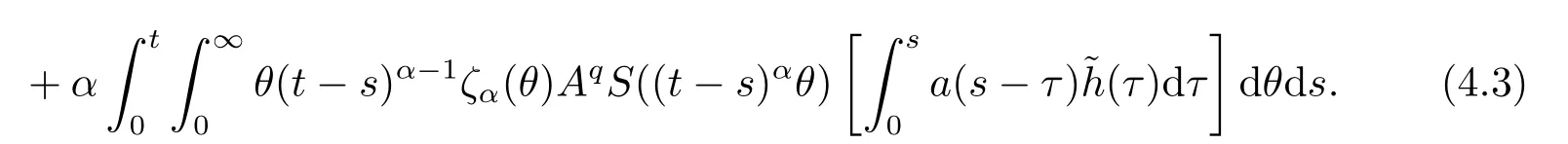


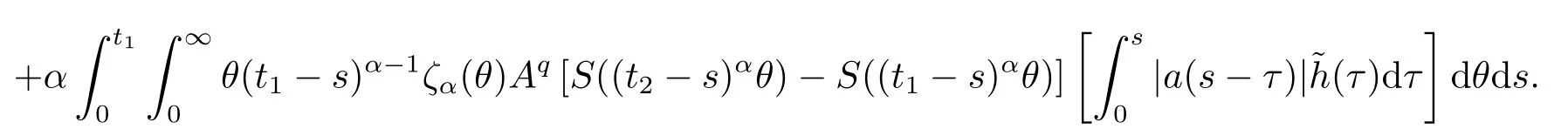
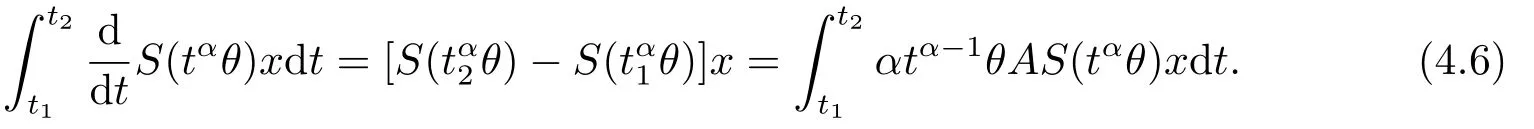







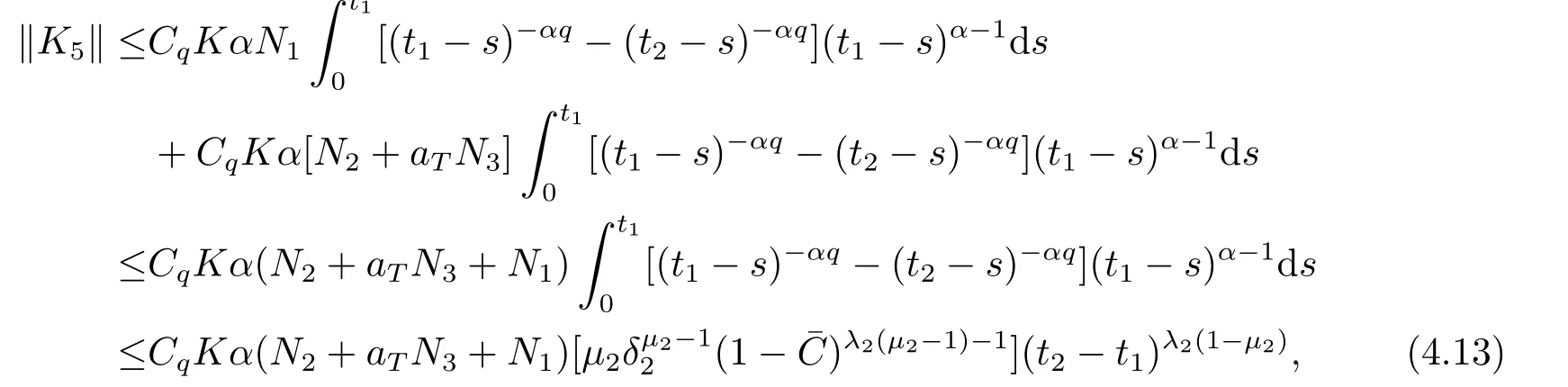

杂志排行
应用数学的其它文章
- Threshold Dynamics of Discrete HIV Virus Model with Therapy
- Solvability for Fractional p-Laplacian Differential Equation with Integral Boundary Conditions at Resonance on Infinite Interval
- Long-Time Dynamics of Solutions for a Class of Coupling Beam Equations with Nonlinear Boundary Conditions
- 基于Markov链的税延型养老保险跨期效用
- 动态投资组合现金次可加风险度量的时间相容性
- 部分线性模型的模态正交经验似然推断
