基于Markov链的税延型养老保险跨期效用

刘华,关雪飘

( 五邑大学数学与计算科学学院,广东 江门529020)

1.引言

2018年5月财政部税务总局下发了财税[2018]22号文的通知,将上海、福建和苏州作为税延养老保险的试点以缓解社会养老保险收不抵支的问题.税收优惠型养老保险有多种模式,大部分在国外已经成熟,而在我国正处于探索阶段,这是因为各国国情和国民消费理念不同.

此前,国内许多学者从各种角度对税收优惠型商业养老保险进行研究.吴祥佑等[1]从社会福利效应的角度证明了免税-免税-征税(Exempting- Exempting-Taxing,EET)模式优于其它税收优惠模式.财税[2018]22号文推出的正是这种EET政策,即商业养老保险的部分保费可以在个税前抵扣而在领取期对部分保额收取税费.马宁[2]分析了前后端税率对消费者效用的影响,并给出了消费者对前端税率更敏感的结论.STANLEY等[3]讨论了保费与消费的投资组合关系对消费和遗产的期望效用的影响.何立新等[4]在终身收入约束下,根据消费最大化效用函数求解家庭的最优储蓄率.白仲林等[5]采用新古典经济学生命周期推导出最优消费路径.乔伟等[6]基于“二元心理系统假设”构建准双曲线贴现模型讨论消费者在跨时期时间偏好动态不一致下对商业养老保险的需求,来评价税延型养老保险政策的可行性.人们是否购买养老保险,主要取决于购买和不购买情况下其一生的效用.而用来衡量效用的可支配收入由缴费额度和领取期数来决定,即取决于个体的健康状态和寿命.个体在任意时点会转到的健康状态是不确定的,这里将引入Markov链转移概率.李晓林[7]在复合生命状态模型中运用Markov 链给出转移概率和转移强度之间的关系,表明了Markov链可以很好的模拟个体健康状态随机变化的特性.张连增等[8]运用Markov链来模拟计算多种健康状态下的保费和准备金.因此我们在跨期效用模型基础上考虑个体的健康状态和时间,构建基于Markov链健康状态的跨期效用模型,进一步分析税延养老保险对个人效用的动态影响.

2.基础模型

乔伟等[6]采用准双曲线模型下的跨期效用函数来研究个体不同时期的效用偏好.跨期双曲线效用模型如下：

个体的效用可以用可支配收入来衡量,C0为当前时期个人的可支配收入(Disposable Personal Income,DPI),Ct表示未来时期的DPI,u(C)=lnC.计算个体一生的效用需要把各个时期的效用折现到当前时期,β为短期贴现因子,δ为长时间偏好贴现因子.当个体在工作前,其一生效用可以表达为：

其中X为经济资源,(1+b)(θ+φ)为社会养老保险的领取额,为社会养老保险缴费基数,b为社会养老保险基金的投资收益率,θ为社会养老保险的个人缴费比率,φ为社会养老保险的企业缴费比率,S表示储蓄率,r为无风险收益率,T2为投资收益税率.

当个体进入工作期后,偏好会随着时间的变动而变动,其一生效用变化为：

3.Markov链跨期效用模型

本文主要对个体处于工作期和退休期的效用进行分析,将跨期效用模型考虑时间以及健康、失能、死亡概率等影响因素.把个体每一期的DPI折现到当期的0时刻来计算其当期的效用,从而比较两种情况下的效用.那么个体一生的效用可表示为：

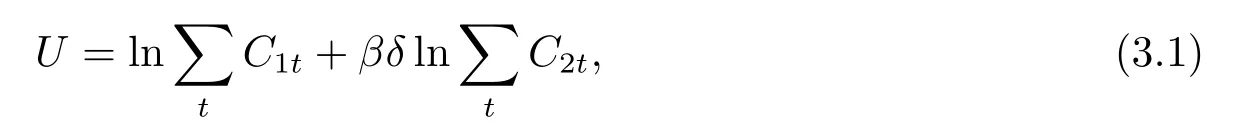
C1t表示工作期t时刻的可支配效用,C2t表示由工作期t时刻健康状态决定的退休期的DPI.在基础模型中,假定了DPI为常数.但实际上个体的身体状况会影响个体在工作期的薪资及储蓄偏好从而影响其效用.在新的模型中,我们区分了个体在不同健康状态下的DPI,来分析健康状态对各期效用的影响.另外生存时间由个体健康状态决定,因而也会影响DPI.

Ⅰ不购买税延养老保险情形下的效用模型

为简便,本文假设个体的储蓄不进行投资,即r=0.在工作期的任意时点,若个体处于健康状态,则其在该时点的DPI有Wd(1−S)=()(1−T1)(1−S),W为个体健康时的工资.若个体到达失能状态,其薪资和社保缴费基数都降低为原来的α倍,此时DPI 变为αWd(1−S)=α()(1−T1)(1−S).若个体在工作期某时刻死亡,则其不会进行储蓄,DPI上升为Wd=()(1−T1).那么,个体在工作期某个时点的期望DPI可表示为：

h+为状态转移概率,表示个体在x岁时处于i状态,在x+t+h岁转到j状态的概率.1为健康状态,2为失能状态,3为死亡状态,个体的健康与失能状态是常返状态,而死亡状态是吸收状态.

一般而言,个体退休时的DPI主要依赖于社会养老保险金和工作期的储蓄,因此个体在工作期的DPI直接影响退休后的DPI.[9]根据个人养老金计算方法,退休后仍然生存的个体,每个月可领到的基础养老金为可消费的工作期储蓄总和为那么个体在退休后的期望DPI可表示为：

B=12,k为养老金领取比例.从而个体一生的效用为：

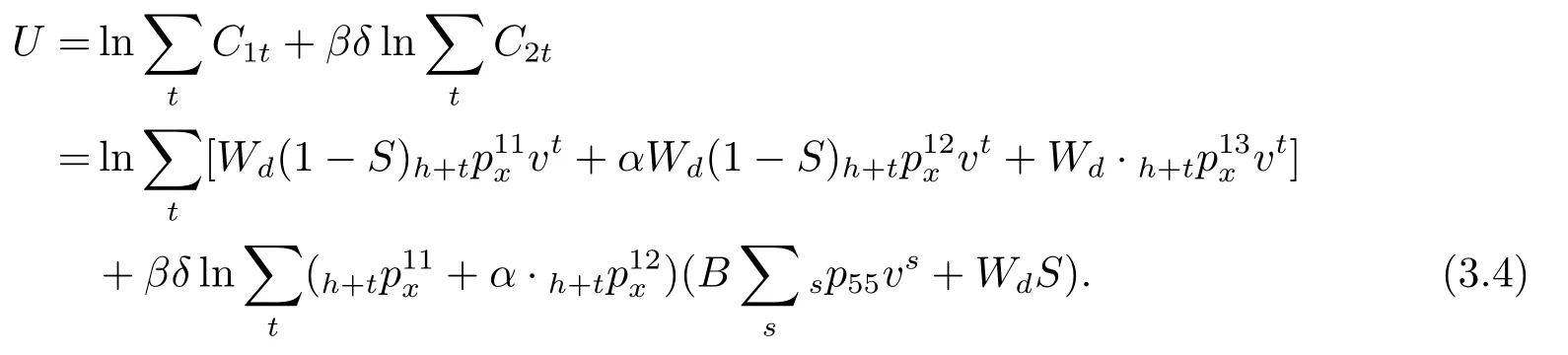
对效用U求关于储蓄率S的导数,计算得

此时个体的一生效用U取得最大值.从上式可以看出,储蓄率S随退休后的生存时间s的变化而变化,各期的可支配收入也随生存时间s的变化而变化.将式(3.5)代入式(3.4)得：

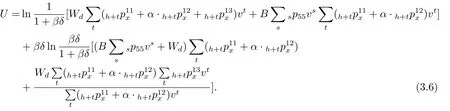
Ⅱ购买税延养老保险情形下的效用模型

据财税[2018]22号文指示,商业养老保险的保费可在税前抵扣,最高可抵扣1000元与6%月工资收入的最小者,即min(1000,6%W).采用平均工资来对比,有min(1000,6%W)=6%W.那么工作期处于健康状态的个体其DPI为[(6%W)T1](1−S∗),S∗为购买税延情形下个体的储蓄率.而处于失能状态的个体,工资下降为αW,此时应缴税费α(6%W)T1.另一方面,个体会因收入减少而降低商业养老保险的保额,对应保费降低为α·P,此时其DPI变为[α()−α(6%W)T1](1−S∗).在工作期到达死亡状态的个体不会进行储蓄和购买商业养老保险,其DPI仍然为()(1−T1).这时,个体在工作期任意时点的期望DPI为：

同样地,个体领取的养老金与缴费基数有关.个体退休后的社会养老金不变,工作期的储蓄变为税延养老保险金按领取额的75%扣税,所以个体每月可领到的商业养老金为这里D=(1+b1)(1−75%T2)P,b1为商业养老保险基金的投资收益率,T2为税延型商业养老保险领取时的税率.

综上,个体退休时的期望可支配收入为：

结合式(3.7)和(3.8),购买税延型商业养老保险的个体的一生效用为：

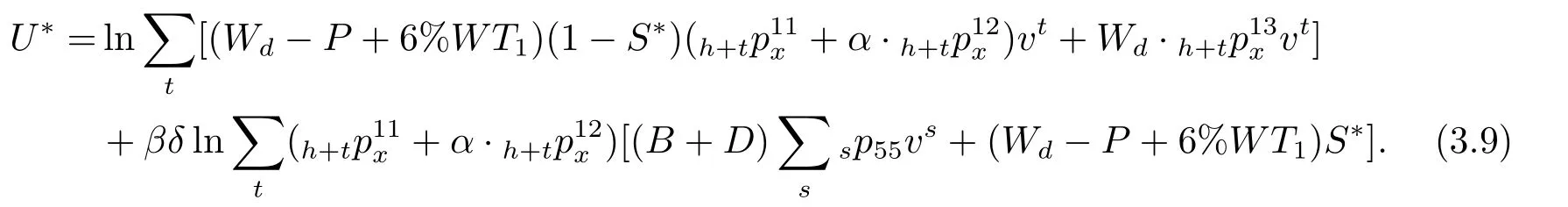
对U∗求关于储蓄率S∗的导数,得：

把储蓄率代入(3.9)式,得：

综上,与不购买商业养老保险对比,购买税延养老保险后,工作期每时刻的健康状态对每个阶段的可支配收入的差额影响为：

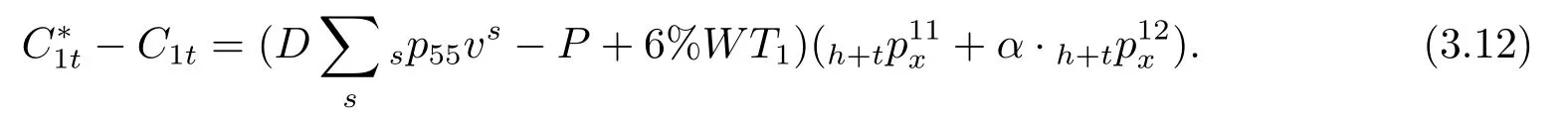
这个结果随着每时刻健康状态的变化而变化,且受生存时长的影响.当差额大于0时,说明此时个体购买税延型商业养老保险后的跨期效用会大于不购买的情形,从而促进国民对商业养老保险的消费,以缓解社会养老保险收不抵支的压力.

4.数值实验

为了使基于Markov链的跨期效用模型能够直观地判断税延型商业养老保险对个体效用的影响,下文将采用具体的数值进行模拟实验.对于基础模型中原有的参数,我们参照文[6]的假设：

1)个体参工年龄为25岁,退休年龄为55岁.我们以30岁的个体为研究对象,即x=30;

2)长期时间偏好因子δ=0.958,短期时间偏好因子β=0.703;

3)社会养老保险的投资收益率b=2.48%,商业养老保险的投资收益率b1=4.515%,贴现率V=1/(1+r)=1/(1+2.837%);

4)社会养老保险个人缴费率θ=8%;

5)商业养老保险的缴费率γ=11.66%,P=γ();

6)个人所得税率为T1=3%.

其它新模型中新增加的和更新的参数如下：

1)2016年城镇单位人员年平均工资为67569元.①数据来源：《中国统计年鉴2017》2012-2016年年平均工资增长率在10%左右,根据这个增长率推算出2018年城镇单位人员年平均工资为81758元,相应的月平均工资为W=81758/12≈6813元;

2)基础养老金领取比例k=1%;

3)失能后个体的薪资会下降,若是永久失能则其下降幅度是最大的,若是短暂性失能则其下降幅度较小,这里假定下降幅度为30%,即α=0.7;

4)社会养老保险的缴费基数取值范围为6%-300%的月工资收入,这里取=W;

5)财税[2018]22号文指定,个人领取商业养老保险金时需要对养老金的75%纳税,税率为T2=10%.

Ⅰ不购买税延养老保险时的效用

把上述参数代入(3.6)式,得到效用：

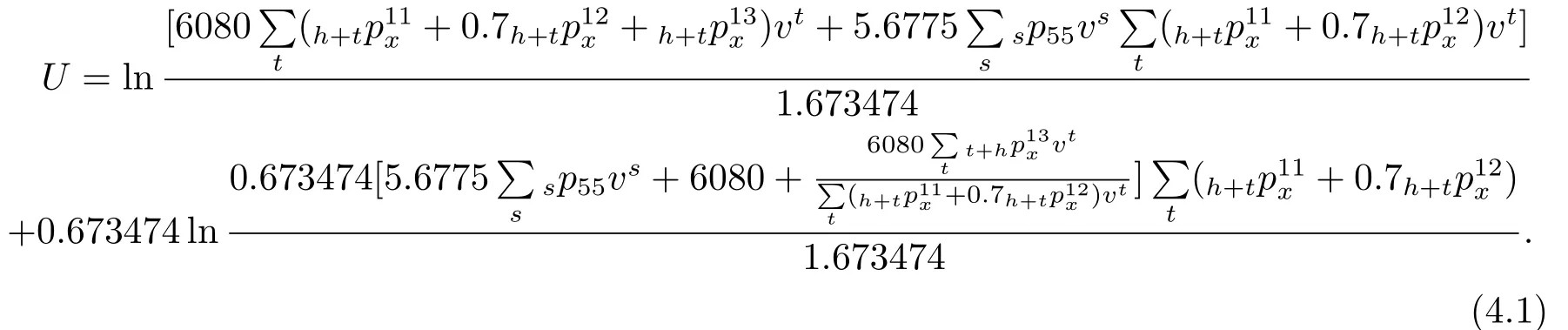
由上式可看出,只要求出每个时期每种状态转移概率就可以求出效用U.在前面我们已经介绍过是Markov链转移概率,由于模型中出现的收入与支出是每月出现一次的,因此我们取步长h=1/12.借助Kolmogorov向前方程和Euler方法,我们可以求得各个状态的转移概率:[10]

这里,概率转移强度满足如下条件：

1)=4×10−4+3.4674×10−6e0.138155x;

2)=5×10−4+7.5858×10−5e0.087498x;

3)=0.1;

4)=.

当t=0时,=1、=0、=0,应用Matlab软件计算出每个时刻各个状态的转移概率如表4.1所示:

表4.1 个体在工作期各时刻对应的健康状态转移概率

由表4.1可以看到,工作期随着时间的增加,个体向失能状态和死亡状态转移的可能性增加,从而使得工资下降或不进行储蓄的可能性增加.

在退休期,只要生存就可以领取养老金和花费工作期的储蓄,因此在退休期我们只需要考虑生存和死亡两状态的Markov链,即模型中只需要计算出55岁的人在55+s岁时仍然生存的概率：

前面已证明个体的效用随着退休后的生存时间s的变化而变化,为简便我们只计算到80周岁,也即领取期为25年.求出各时刻的sp55,在表4.2中给出：

表4.2 个体在退休期每个时刻对应的生存概率

通过简单的计算,不购买税延型养老保险情况下个体一生效用总和最大为22.89997.

Ⅱ购买税延养老保险时的效用

将参数代入(3.11)式得到30岁个体购买税延养老保险时的最大效用：

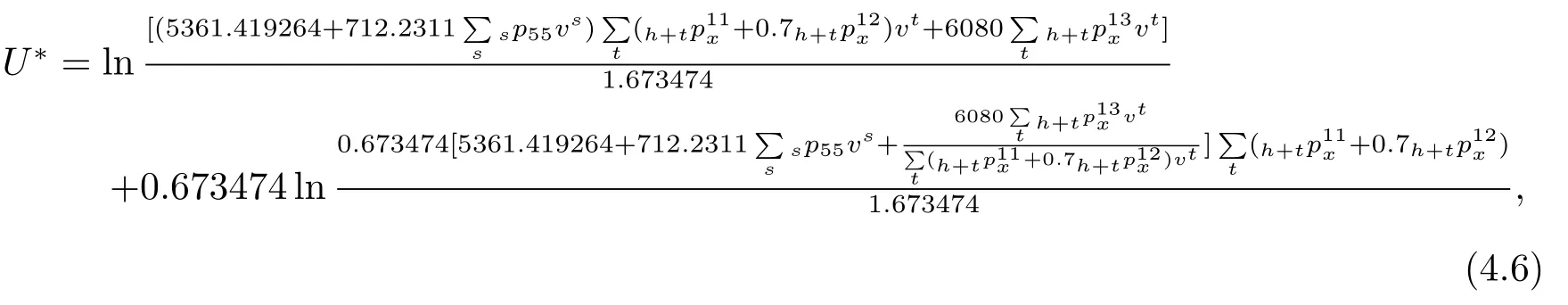
Ⅲ两种情形下的效用对比

个体的当期效用主要由当期的可支配收入来衡量,根据式(3.12)求得工作期每时刻的健康状态对两个时期的可支配收入的影响差额为使用Matlab画出生存时长和健康状态对两种情形下的可支配收入差额影响的函数图像如下：

图4.1 生存时长和健康状态变化对两种情形的DPI差额的影响

首先,从图4.1中可以看到,两种情形下每时期的可支配收入差额对退休后的生存时长s较敏感,退休后的生存时间越长可支配收入差额越大.这是因为个体生存时间越长,领取期数就越多,购买税延型养老保险的个体可以得到更多的商业养老金；其次,对于工作期任意时刻t来说,个体越接近退休时刻,购买与不购买税延养老保险的可支配收入差额越小.从表4.1可以看到个体在工作期越接近退休时刻,其健康状态越恶劣,由健康状态转到失能状态的概率会变大,薪资下降从而降低各类缴费基数,同时也降低了税延养老保险的缴费和享领金,因此个体接近退休时刻会减小两种情形的可支配收入差额; 最后,从上图中可以看到只要个体在退休后至少存活1个月,即s ≥1/12,都有而《2015年世界卫生统计报告》指出,中国人口平均寿命为75岁,可证明购买税延型养老保险的个体无论在工作期还是退休期都有更多的可支配收入,他们终身效用更高.

5.总结

本文在跨期效用模型的基础上,加入健康状态和时间因素,通过构造基于Markov链跨期效用模型来更加准确地评价税延养老保险施行的效果.从工作期与退休期总的效用来看,个体购买税延型养老保险要比不购买时得到更多的效用.从各期的可支配收入来看,一方面,个体的生存时间越长,购买税延型养老保险会使个体获得更多的可支配收入,且随着时间的增加,可支配收入的差额会加大.另一方面,个体健康状态恶化会减少个体总体的可支配收入,从而降低税延养老保险带来的效用.

基于Markov链的跨期效用模型实验证明,购买税延养老保险在总体上会增加个人的终身效用.但对于健康状况较差的个体,能领到的养老金较少,若购买税延养老保险,反而会降低其效用.因此在设计税延养老保险时,企业需要考虑各种健康状况的人群的需求,给予个体一定的返还,例如保证领取一定数量的保险金,这样有利于税延养老保险政策的普遍实施.