动态投资组合现金次可加风险度量的时间相容性
2020-01-10刘红卫肖彩波
刘红卫,肖彩波
(1.西藏大学理学院,西藏 拉萨850000; 2.河北经贸大学公共管理学院,河北 石家庄050061)
1.引言
经典的风险度量模型VaR由于不满足分散投资能减少风险这一市场基本要求,因此,文[1]利用公理化的方法提出了一致风险度量的概念,奠定了公理化方法研究风险度量的基础.由于货币流动性特征,一致风险度量中的正齐次性在实际金融市场中并不能满足.文[2-3]分别独立的推广了一致风险度量,在弱化一致风险度量中正齐次性和次可加性的基础上,提出了凸风险度量.
风险度量公理化体系中单调性和凸性已得到广泛的认可和使用,但从金融的角度来看,现金可加性(即平移不变性)存在一些争议.一个最根本的原因在于金融投资机构要用当前的准备金来覆盖未来的风险,存在货币度量不在同一时间点上的问题.由于货币具有时间价值,这样会产生准备金与金融头寸度量单位不一致的问题,导致现金可加性与实际金融市场不相符.为了克服这种缺陷,文[4]提出把风险度量定义在折现头寸集合上,一定程度上解决了风险头寸与风险度量测量时间点不同的问题.事实上,当折现因子是常数时,采用这种折现的方法避免了准备金与金融头寸取值不在同一时间点上问题,但当折现因子是随机时,折现因子本身也会携带风险,也就是说,对未来金融头寸的折现会有新的风险进入,这就违背了风险度量仅对未来风险头寸进行度量的初衷.考虑到风险资产和折现因子的随机性,文[5]依据货币的时间价值,把静态风险度量中的平移不变性(现金可加性)条件弱化为现金次可加性,用ρ(X+m)≥ρ(X)−m,m ≥0来表示,建立了现金次可加风险度量的研究框架,并利用扩大空间的方法给出了相应的表示定理,文[6]把文[5]的结论推广到投资组合的情况,建立了投资组合现金次可加风险度量研究框架,并给出了相应的表示定理.
以上关于风险度量的文献仅对未来风险头寸的当前风险进行了研究,这类风险称为静态风险度量.事实上,随着时间的不断推移,信息的不断累积,风险评估可以得到不断的更新,这种动态评估风险的方法称为动态风险度量.表现在理论上就是一列条件风险度量(ρt)t∈[0,T].文[7-8]提出了条件风险度量的研究框架,并给出了动态凸风险度量的表示定理.时间相容性是动态风险度量最重要的性质之一,它刻画了不同时刻风险度量之间的关系.动态风险的时间相容性可通过可接受集、惩罚函数、测度等来等价刻画,其中文[7]通过惩罚函数、粘合测度等方法研究了时间相容性的性质.文[9-10]通过可接受集分解,研究了动态凸风险度量中强时间相容性的性质.关于动态风险度量时间相容性的研究还可以参阅文[11-12].
目前,动态风险度量的研究主要集中在单个金融头寸的情况,虽然集合值的动态风险度量在文[13-14]进行了研究,但基于数量值角度对动态投资组合风险度量进行研究的文献较少.本文主要把文[15-16]中的静态投资组合凸风险度量推广到动态现金次可加情形进行研究,建立条件投资组合现金次可加风险度量的研究框架,给出相应的表示定理.进一步研究了动态投资组合现金次可加风险度量在满足一些假定条件下的时间相容性问题.
2.准备知识
文[5]把金融风险公理化中的现金可加性条件弱化到了现金次可加性,建立了现金次可加风险度量的框架,并给出了相应的表示定理.文[15-16]从数量值角度出发,提出了投资组合现金可加风险度量的研究框架,并给出了相应的表示定理,以下结果主要来自文[5,8,16].
定义2.1[5]若映射R:X→R满足下列三条公理:
1)单调性:对所有满足X ≤Y的X,Y ∈X,有R(X)≥R(Y).
2)现金次可加性:对所有的X ∈X和任意的m ∈R+,有R(X+m)≥R(X)−m.
3)凸性:对所有的X,Y ∈X和任意的0≤λ ≤1,,有R(λX+(1−λ)Y)≤λR(X)+(1−λ)R(Y).
则称映射R为现金次可加风险度量.
现金次可加性充分考虑到了货币的时间价值,是现金可加性的推广.其中X是将来某一时刻金融头寸的集合.对任意的X ∈X和m ∈R+,现金次可加性等价形式还可表示为:R(X+m)+m是m的非减函数.
若现金次可加风险度量R满足正齐次性,即对任意的λ ≥0,有R(λX)=λR(X),则称R是一致现金次可加风险度量.称有限可加测度µ为次概率测度,若µ ∈M1,f(X),且µ(Ω)≤1,其中M1,f表示有限可加概率测度的全体,用Ms,f(X)来表示次概率测度的全体.
引理2.1[5]设R:X→R是现金次可加风险度量,则R具有下列的表示形式:
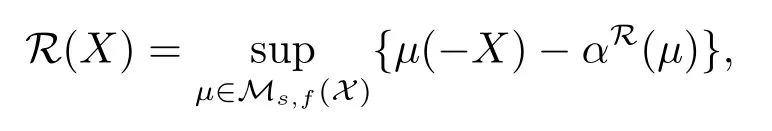
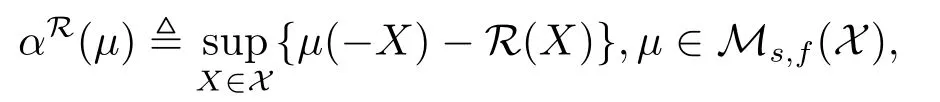
其中αR称为现金次可加风险度量R的惩罚函数.
定义2.2[16]若映射ρ:Xd→R满足如下性质:
1)单调性:对所有满足X1≤X2的X1,X2∈Xd,有ρ(X1)≥ρ(X2);
2)现金可加性:对所有的X∈Xd和任意的实数m,有
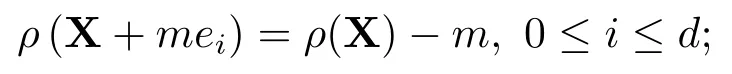
3)凸性:对所有的X1,X2∈Xd和任意的λ ∈[0,1],有
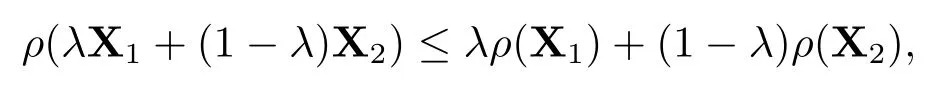
则称映射ρ为投资组合凸风险度量.
引理2.2[16]设映射ρ:Xd→R为投资组合凸风险度量,则ρ有如下的表示形式:
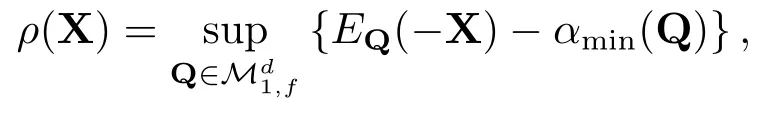
其中αmin(Q)为
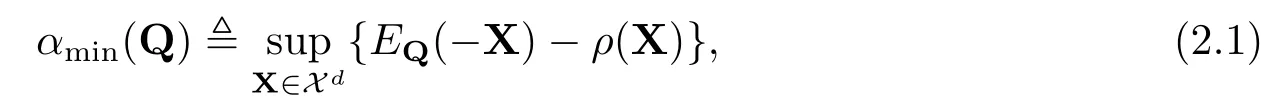
并且αmin是ρ的最小惩罚函数,即对ρ的任意惩罚函数α和满足(2.1)式的αmin,有
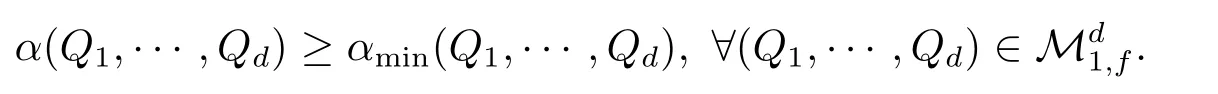
进一步,ρ满足从下连续性时,投资组合凸风险度量ρ还有如下的表示形式:
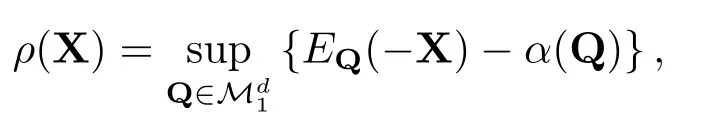
引理2.3[8]设(Ω,F,P)是概率空间,记L0(){X| X:Ω→,σ(X)⊂F},其中[−∞,+∞],H ⊆L0().集合D(H){Z ∈L0()|Z ≥X,∀X ∈H} 是非空的,则存在唯一的随机变量X∗∈D(H),对任意的Z ∈D(H),有X∗≤Z.此外,若H是定性向上的,即对于任何X1,X2∈H,存在X ∈H使得X ≥max {X1,X2},有
1)存在递增的序列(Xn)n∈N ∈H,使得Xn ↗X∗;
2)如果ess supH的期望存在,则有EP(ess supH)=
设T >0是一固定的时间,(Ω,F,Ft,P)是完备的域流空间.Lp(Fi)Lp(Ω,Fi,Ft,P),当1≤p < ∞时,Lp(Fi)表示在域流空间(Ω,Fi,Ft,P)上关于Ft可测的p阶矩存在的随机向量全体.当p=∞时,L∞(Fi)表示在域流空间(Ω,Fi,Ft,P)上所有的关于Ft可测的本性有界随机向量的全体.用正的随机向量X来表示收益,负随机向量−X来表示损失.F0={Φ,Ω},FT=F.D{Dt|Dt ∈Ft,0≤Dt ≤1,t ∈[0,T]}.L(Fs)L(Ω,Fi,Fs,P)来表示所有定义在(Ω,Fi,Fs,P)上关于Fs可测随机变量的集合.定义如下的概率测度集
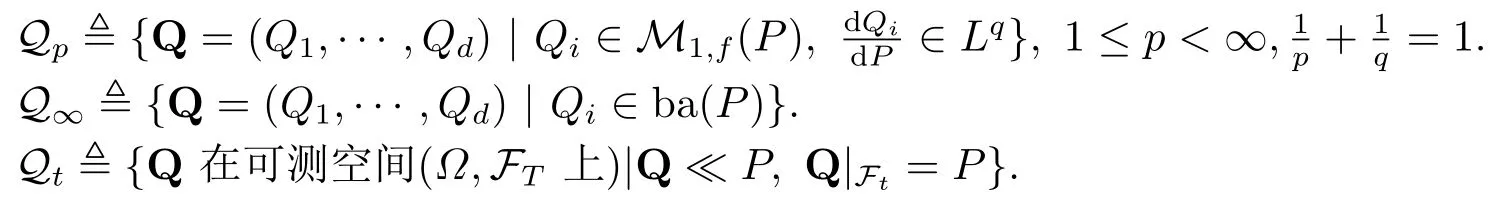
用符号Q来表示Qp ∪Q∞.
3.主要结论
本小节主要从货币的时间价值出发,首先提出了动态投资组合现金次可加风险度量的研究框架,并给出相应的表示定理.进一步,研究动态投资组合现金次可加风险度量在满足一定条件下的时间相容性问题.把文[15-16]的静态投资组合风险度量的研究框架推广到动态现金次可加框架下进行研究,弥补了在投资组合风险度量中货币度量单位不在同一时间点上的不足.
定义3.1对任意的X∈Lpd(Ft),s,t ∈[0,T],且s ≤t,映射ρs,t:Lpd(Ft)→L(Fs)满足下列性质:
1)ρ0,t是一个静态投资组合风险度量;
2)ρt,t(mei)=−m,对于任意的m ∈L(Ft).
则称ρs,t为条件投资组合风险度量.
定义3.1中的性质1)的金融含义为,当在起始时刻s=0计算风险时,条件投资组合风险度量就退化到了ρ0,t:Lpd→R静态投资组合风险度量的情形.性质2)的金融含义为,在到期日t时,所有的信息均已被披露,金融头寸的收益可以视为一个“常数”.
定义3.2若条件风险度量ρs,t:Lpd(Ft)→L(Fs)对s,t ∈[0,T],且s ≤t,满足如下性质
1)单调性:对所有满足X1≤X2的X1,X2∈Lpd(Ft),有
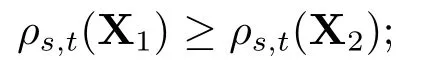
2)现金次可加性:对所有的X∈Lpd(Ft)和任意的m ∈L+(Fs),有
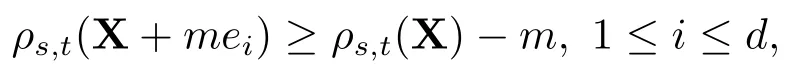
集合L+(Fs)表示在L(Fs)上非负的,且关于Fs可测的随机变量的全体;
3)凸性:对所有的X1,X2∈Lpd(Ft)和任意的Λ∈L(Fs),且0≤Λ≤1,有
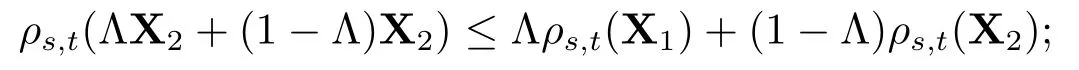
(4)正则性:ρs,t(0)=0.
则称条件风险度量ρs,t为条件投资组合现金次可加风险度量.
条件投资组合现金次可加风险度量有如下的金融解释:单调性表示收益越大,相应的风险越小; 现金次可加性表示在X某个头寸上追加m单位的现金,相应的风险减少的并没有m那么多; 凸性表示分散投资能较少风险; 正则性在某种意义下指无损失就无风险.
性质3.1设映射ρt:Lpd(F)→R,且定义
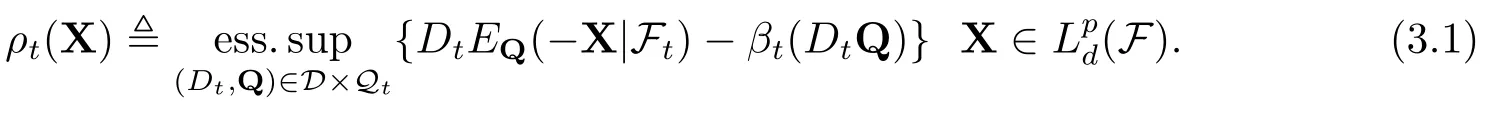
则ρt是条件投资组合现金次可加风险度量.
证单调性:设X1,X2∈Lpd(F),X1≥X2,两边取期望
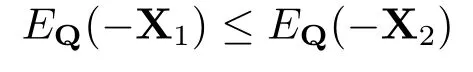
从而有
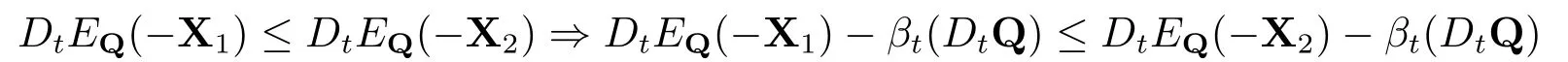
在(D,Q)∈D × Qt上,对上式两边取本性上确界,不等式仍然是成立的.因此就有ρt(X1)≤ρt(X2).
凸性:假设λ是Ft可测的随机变量,且满足0≤λ ≤1,对于任意的X1,X2∈Lpd(F),有
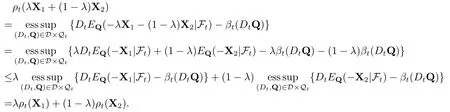
现金次可加性:设m是Ft可测非负的随机变量.对任意的X∈Lpd(F),有
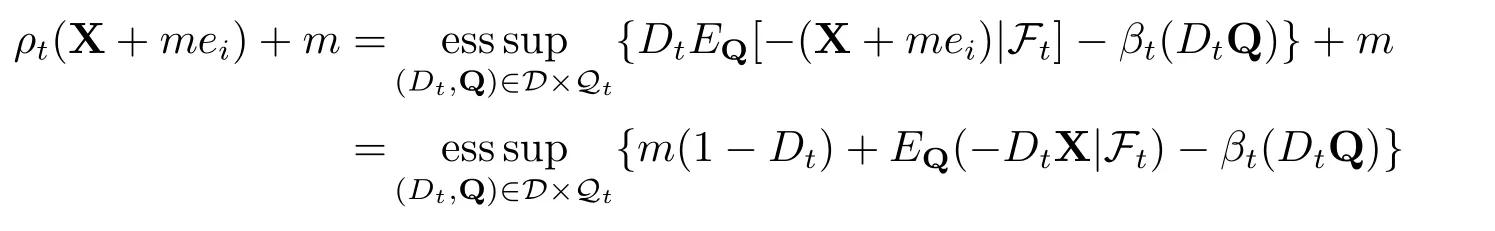
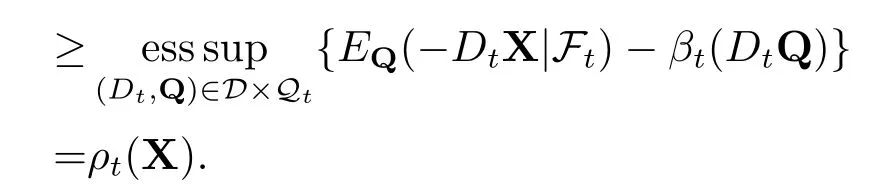
于是就有ρt(X+mei)≥ρt(X)−m.
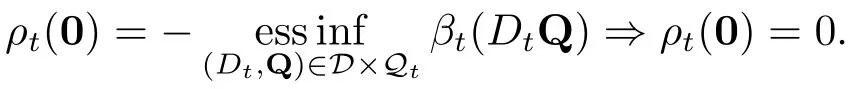
因此,根据定义3.2可知,满足(3.1)式的ρt是条件投资组合现金次可加风险度量.命题得证.
定义3.3如果条件投资组合风险度量ρt:L∞d(F)→R对于任意的A ∈Ft,X,Y∈L∞d(F),满足
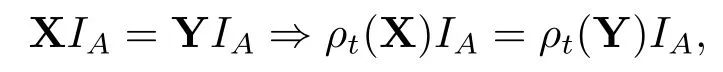
则称条件投资组合风险度量ρt是规范的.
定理3.1设ρt:Lpd(F)→L(Ft)是条件投资组合现金次可加风险度量,是有限的,且则下列性质是等价的.
1)ρt是从上连续的:(Xn)n∈N⊂Lpd(F),Xn ↘X,有ρt(Xn)↗ρt(X).
2)ρt有如下的表示形式
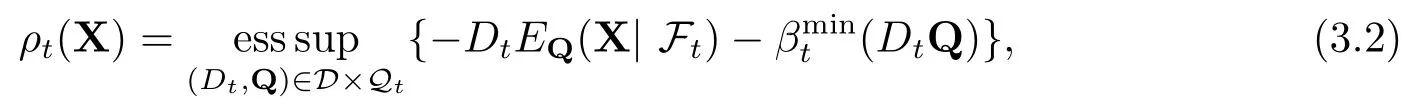
其中
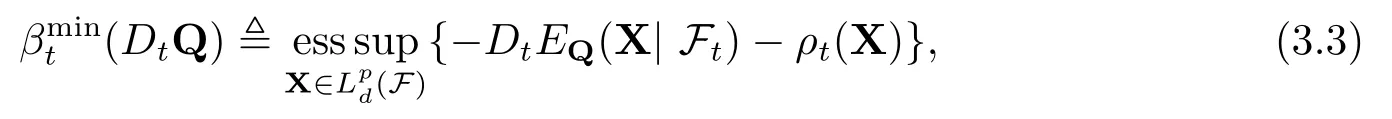
并且是ρt的最小惩罚函数,即对ρt的任意惩罚函数βt,均有
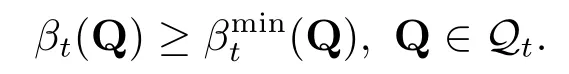
证2)⇒1),ρt可通过(3.2)式来表示.设Xn ↘X,有单调收敛定理可得
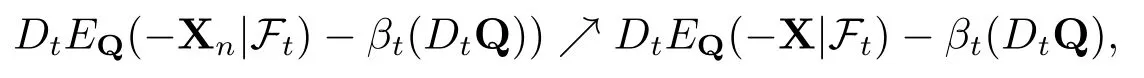
其中Q∈Qt.于是就有
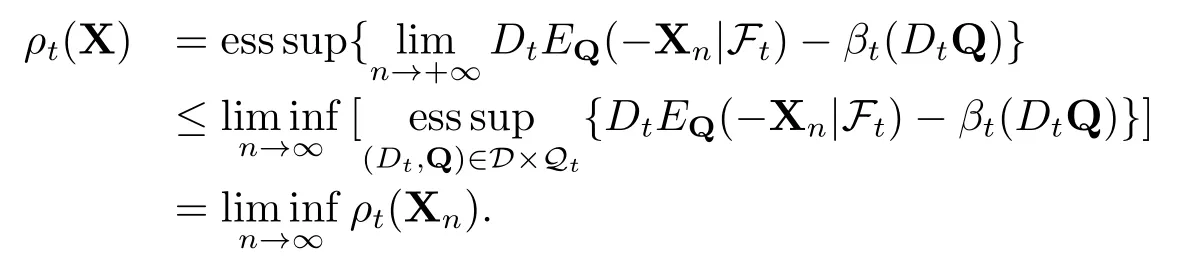
另一方面,ρt的单调性暗含了
1)⇒2),ρt是从上连续的,要证
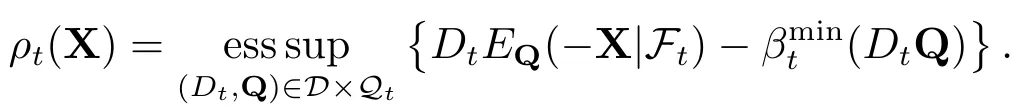
由的定义(3.3)式可得
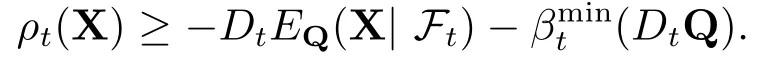
在上式右边取本性上确界不等式关系仍然保持,即有
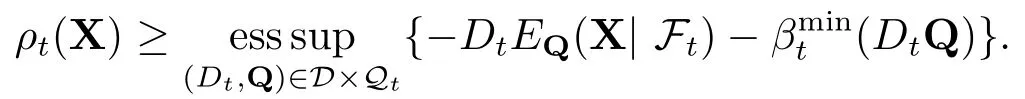
下证相反的不等式.对任意的X∈Lpd(F),等价于证明如下不等式成立
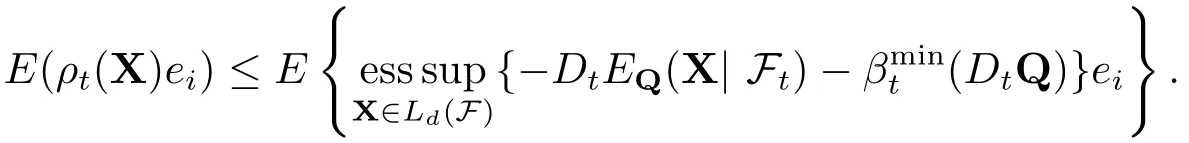
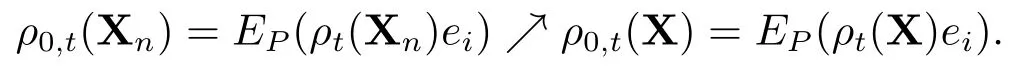
由投资组合现金可加风险度量的表示引理2.2 可知,ρ0,t可表示为如下形式
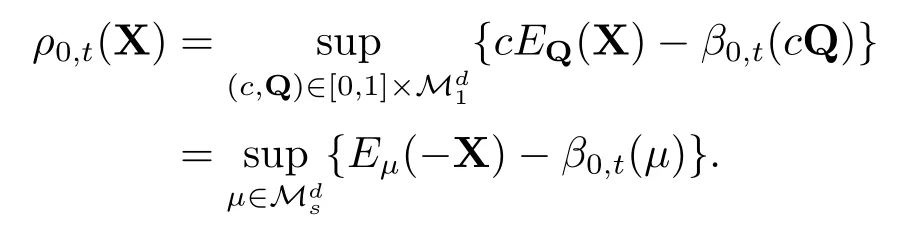
接下来证明,存在随机折现因子Dt ∈Dt使得
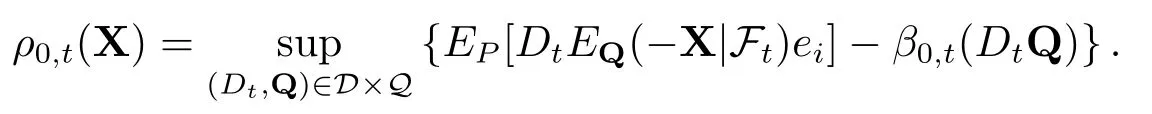
次概率测度可以分解为µ=cQ,c ∈[0,1]为常数折现因子,Q∈Md1,Q≪P.ρ0,t的表示定理中Q是σ可加的,暗含了相应的惩罚函数β0,t(µ)< ∞.下证,存在Dt ∈D,∈Q满足,
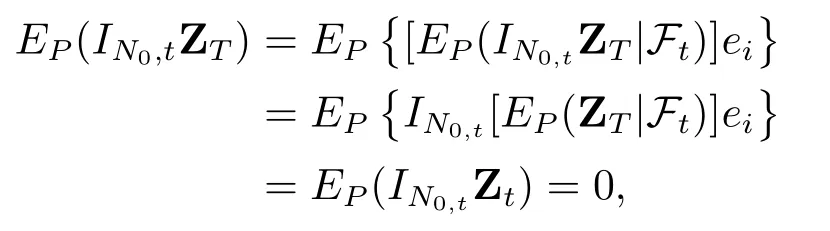
且由于IN0,tZT ≥0,于是可得IN0,tZT ≡0是几乎处处成立的.
定义
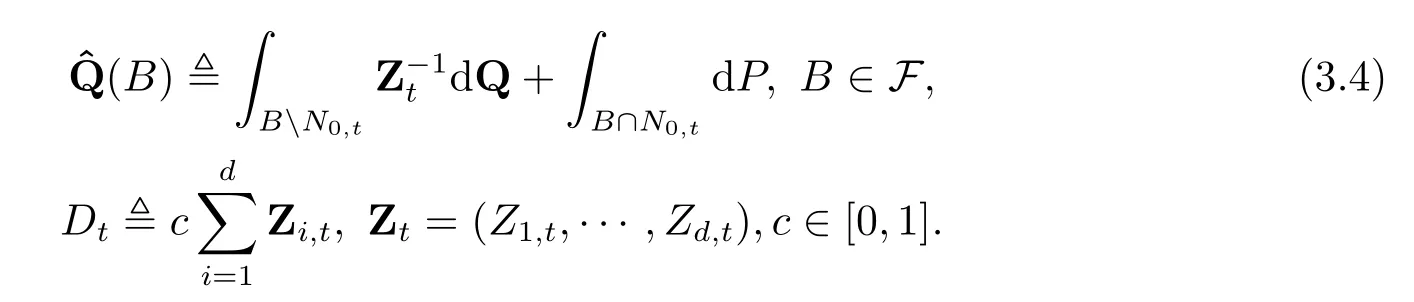
因此Dt ≥0,且在N0,t上有Dt=0,而且是一个概率测度.下证在Ft上有=P.对于任意的B ∈Ft,由(3.4)式可得
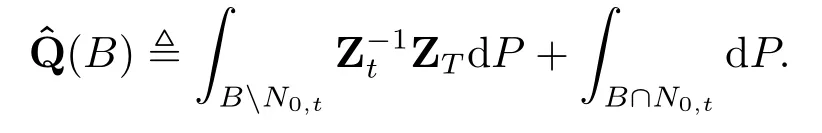
由于BN0,t ∈Ft,根据条件期望的性质,就有
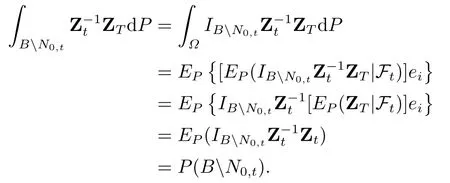
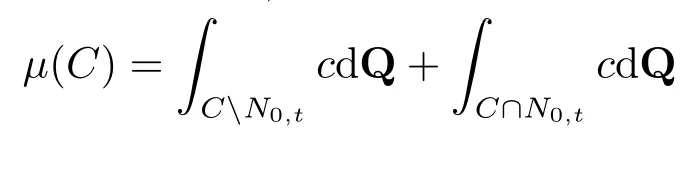
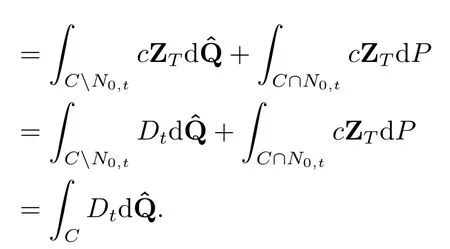
由于IN0,tZT ≡0,在域流Ft上=P可得
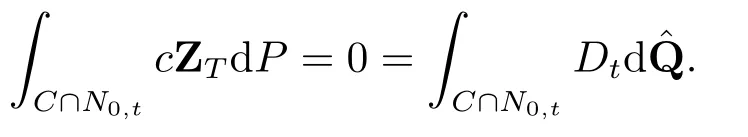
因此就有µ=.
接下来证明Dt ≤1.采用反证方法,设P(Dt >1)>0,A={ω:Dt(ω)>1}.由于Dt是Ft可测的,于是就有A ∈Ft.
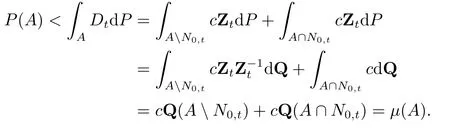
由于ρt具有凸性,易知ρt是规范的.由ρt的规范性可得
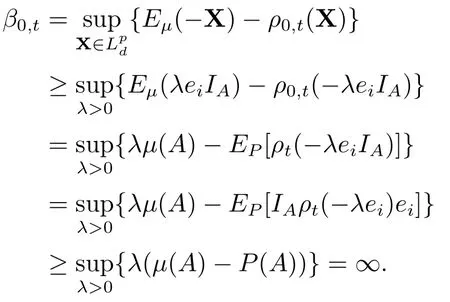
这与β0,t <∞是相互矛盾的,因此,0≤Dt ≤1.
于是就有下式
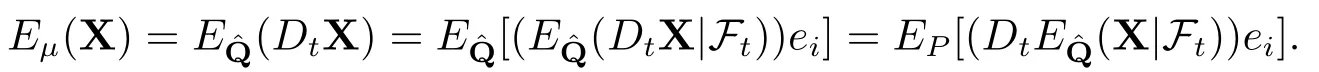
因此,惩罚函数β0,t可记为
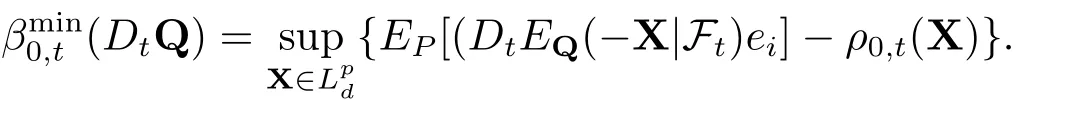
接下来证明EP(βmint(DtQ))=β0,t(DtQ),对于(D,Q)∈D×Qt是成立的.定义CD,Q{DtEQ(−X| Ft)−ρt(X)|X∈Lpd},则有CD,Q是定性向上的.事实上,如果X1,X2∈Lpd.定义ZX1IA+X2IAc ∈Lpd,其中A有下式给出
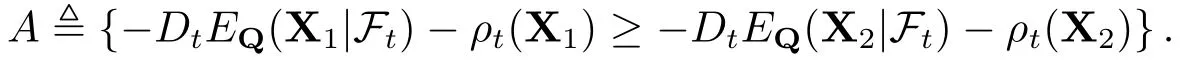
显然A ∈Ft.由ρt具有规范性可知
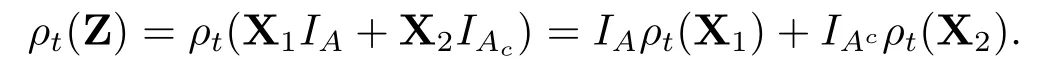
于是就有
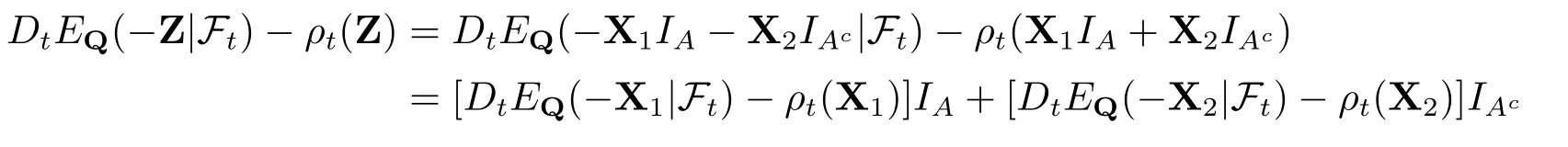
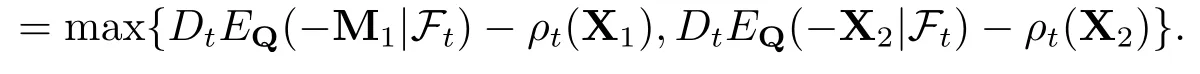
因此,CD,Q是定向向上的.由引理2.3可知,对任意的(D,Q)∈D×Qt,有
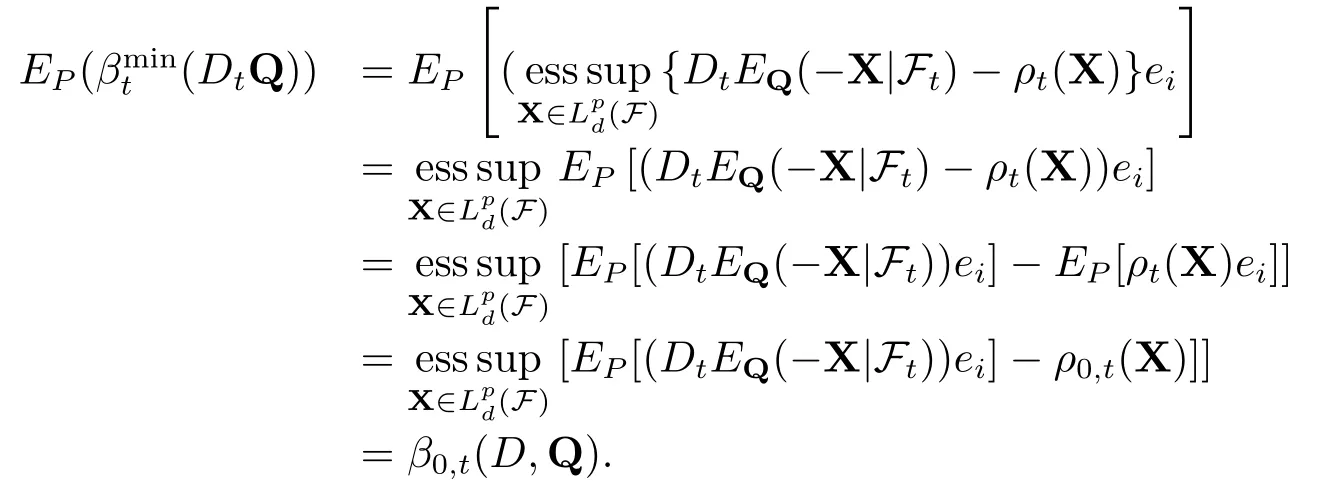
于是就有
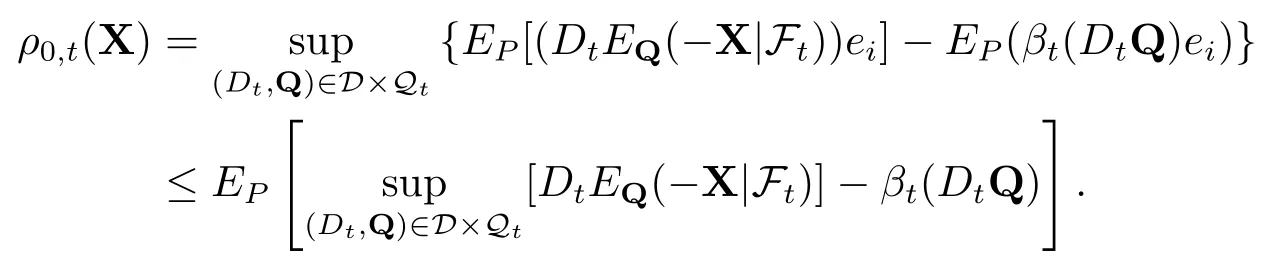
对于为ρt的最小惩罚函数易得.命题得证.
当仅研究期初和期末两个时间点的投资组合风险度量问题时,定理3.1就退化为文[6]的定理4.10.当研究对象由投资组合变为单个资产时,定理3.1就退化为引理2.1.
时间相容性是动态风险度量中一个很重要的性质,它描述了不同时刻间风险度量的关系.在动态投资组合现金可加风险度量中,只要其可接受集、惩罚函数或在不同域流空间上的测度满足一定条件下,动态投资组合现金可加风险度量就具有时间相容性.但对于动态投资组合现金次可加风险度量,还需要附加一些条件,自身才具有时间相容性.
定义3.4设ρt:Lpd(F)→L(Ft)是条件投资组合现金次可加风险度量,则序列(ρt)t∈[0,T]称为动态投资组合现金次可加风险度量.
记Ds,t{Ds,t| Ds,t ∈[0,1],Ds,t ∈Fs,s,t ∈[0,T],s ≤t},Qs,t{Q|Q≪P,Q|Fs=P}.(ρs,t)s,t∈[0,T]是动态投资组合现金次可加风险度量,根据定理3.4其表示定理有如下形式:
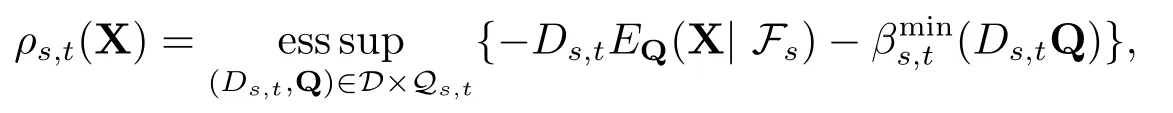
其中X∈Lpd(Ft),Ds,t视为随机折现因子,是ρs,t的最小惩罚函数,且关于Fs是可测的.单位向量ei的下标i是任意固定值.
对不同域流空间上的概率测度Qs,t,惩罚函数βs,t和随机折现因子Ds,t等做如下假设.
(a)概率测度集Qs,t满足:
(a1)设r,s,t ∈[0,T],且r ≤s ≤t,任意的Q1∈Qr,s,Q2∈Qs,t,存在粘合测度Q∈Qr,t,使得
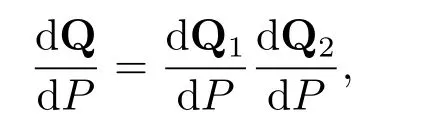
即对任意的X∈Lpd(Ft),有EQ(X|Fr)=EQ1[(EQ2(X|Fs)|Fr)ei];
(a2)对任意的Q1∈Qr,s,Q2∈Qs,t和A ∈Fr,存在Q∈Qr,t,使得
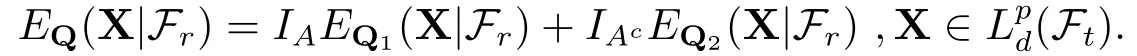
(b)对任意的Q1∈Qr,s,Q2∈Qs,t,D1∈Dr,s,D2∈Ds,t,r,s,t ∈[0,T],且r ≤s ≤t,存在Q∈Q,D ∈D,使得
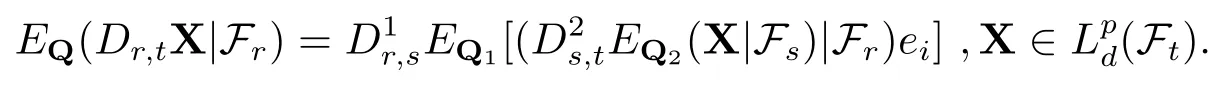
(c)对任意的D1s,t ∈Ds,t,D2s,t ∈Ds,t,A ∈Fs,s,t ∈[0,T]且s ≤t.随机折现因子Ds,t ∈D满足
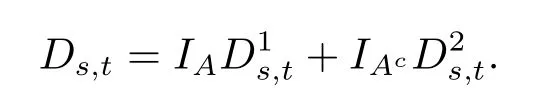
(d)对惩罚函数β满足:
(d1)对任意的Q∈Q,D ∈D,r,s,t ∈[0,T],且r ≤s ≤t,有
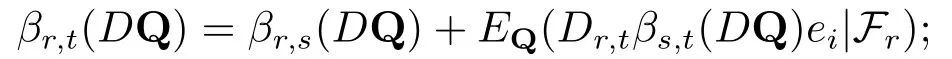
(d2)对任意的Q1,Q2∈Qs,t,D1s,t,D2s,t ∈Ds,t,A ∈Fs,s,t ∈[0,T],且s ≤t,有
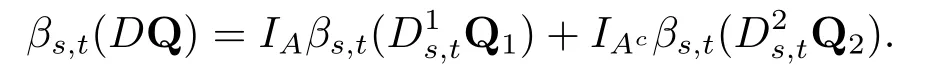
定理3.2当Q,D和惩罚函数βt满足(a),(b),(c)和(d)假设时,动态投资组合现金次可加风险度量(ρt)t∈[0,T]满足时间相容性.
证令s ≤t ∈[0,T],X∈Lpd(Ft).首先证明集合
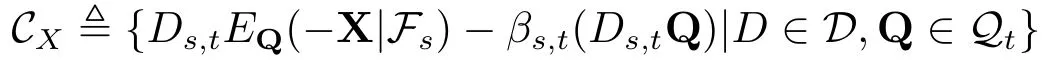
是定向向上的,定义
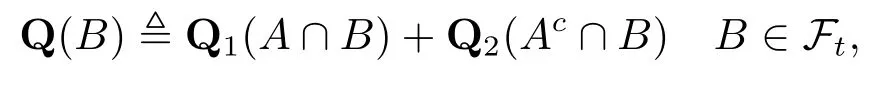
其中
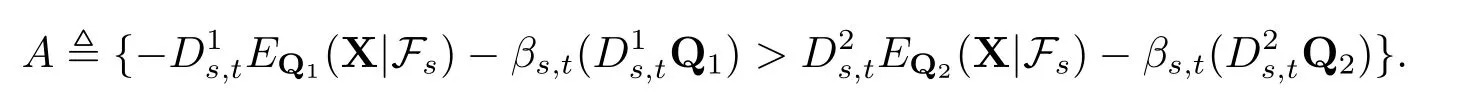
显然A ∈Fs.根据(a),(c)和(d)的假定,于是有
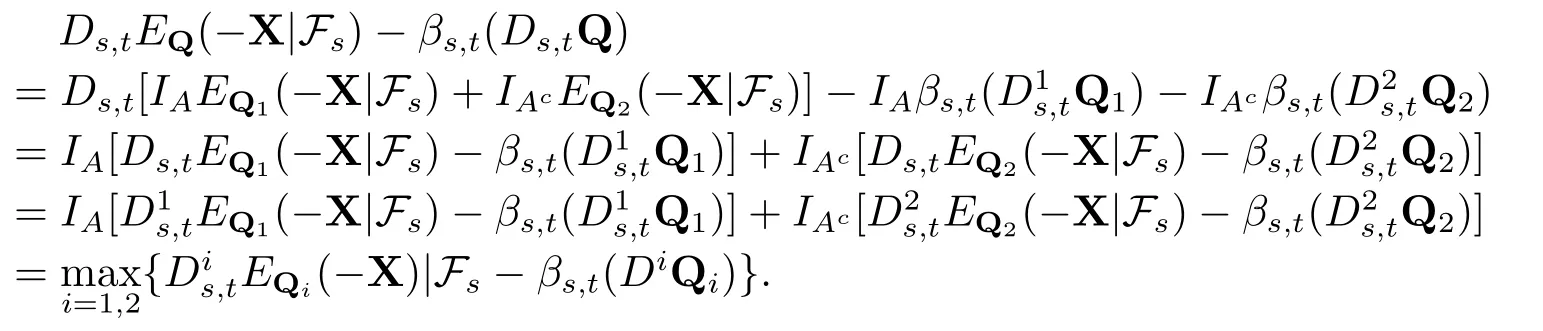
因此集合CX是定向向上的.所以,存在一个递增序列CX,使得
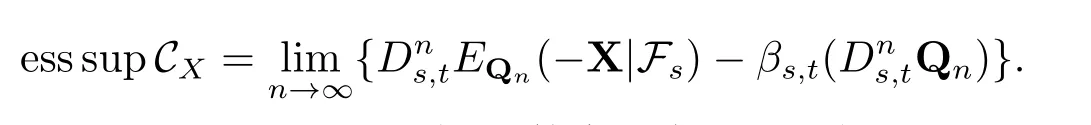
对任意的r,s,t ∈[0,T],且r ≤s ≤t.由ρr,t的表示定理以及假设(b)和(d)可得
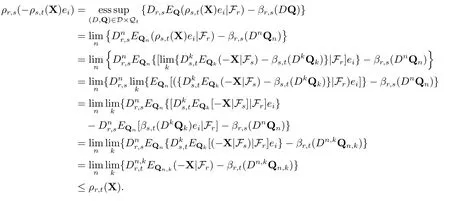
下证反向不等式ρr,s(−ρs,t(X))≥ρr,t(X),由ρr,t的表示定理及假设(a),(b),(d)和Fatou引理可得
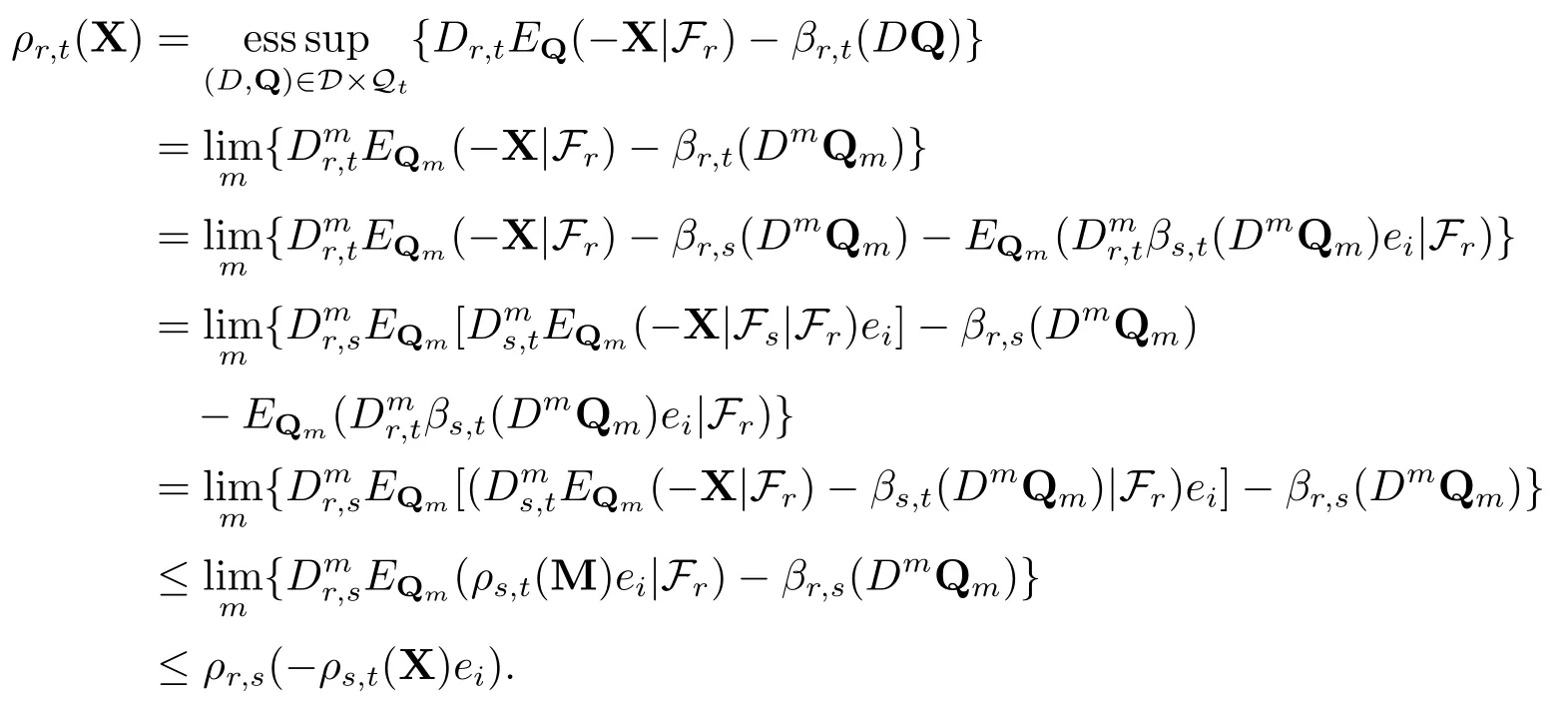
于是就有ρr,t(X)=ρr,s(−ρs,t(M)).命题得证.
性质3.2设(ρt)t∈[0,T]是动态投资组合现金次可加的风险度量,若ρt满足弱时齐性,对任意的s,t ∈[0,T],且s ≤t,X∈Lpd(F)有
1)如果ρt(X)≤0,则ρs(X)≤ρs(−ρt(X)ei);
2)如果ρt(X)≥0,则ρs(X)≥ρs((−ρt(X)ei).
证1)对任意的s,t ∈[0,T],s ≤t,X∈Lpd(F),ρt(X)≤0.由ρt的正则性可知ρt(0)=0.由ρt的现金次可加性得
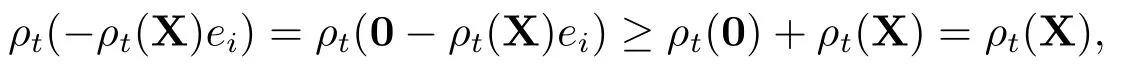
ρt满足弱时齐性,于是就有
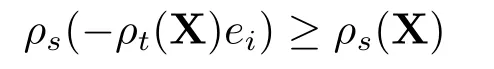
2)利用1)类似的方法,结论易证.
4.结语
本文基于货币具有时间价值这一金融市场实际,在一般空间LPd(Ft)上建立了动态投资组合现金次可加风险度量的研究框架,利用风险度量公理化定理给出了动态资产组合现金次可加风险度量的概念,并给出了相应的表示定理,推广了文[5,15-16]关于静态投资组合风险度量和现金次可加风险度量的结论.并讨论了概率测度、惩罚函数和随机折现因子在满足假定条件下动态投资组合现金次可加风险度量的时间相容性问题.
