均值-方差准则下具有利率和通胀双重风险的资产负债管理问题

潘坚,赵攀

(1.赣南师范大学数学与计算机科学学院,江西 赣州341000;2.皖西学院金融与数学学院,安徽 六安237012)

1.引言

1952年,诺贝尔经济学家Markowitz在他开创性的论文中提出了均值-方差模型[1],奠定了现代投资组合选择理论的基石.经典的Markowitz模型只考虑了单期静态情形,后来学者们致力于把它推广到更符合实际的多期和连续时间情形.然而,由于方差没有可分性,导致多阶段和连续时间均值-方差模型不能直接用动态规划方法求解.直到2000年,香港中文大学LI和Ng[2]以及ZHOU和LI[3]利用嵌入法和随机线性二次控制方法分别给出了离散多阶段和连续时间均值-方差问题的有效投资策略及有效前沿的解析表达式,更多满足现实条件的动态均值-方差模型才得到了解决.这其中,有不少学者研究了均值-方差准则下的资产负债管理问题.如,Leippold等[4]运用几何方法和嵌入法得到了离散多周期资产负债管理问题有效投资策略及有效前沿的解析表达式; Chiu和LI[5]在文[4]的基础上研究了连续时间的资产负债管理问题并得到有效投资策略和有效前沿的解析表达式,其中累积债务的演化过程服从几何布朗运动; 谢树香和李仲飞[6]利用文[3]的方法研究了累积债务的演化过程服从算术布朗运动的资产负债管理问题并得到连续时间资产负债管理问题的资产配置策略; CHEN等[7]与XIE[8]分别将文[5-6]推广至市场有机制转换的情形并得到有效的投资策略; CHANG[9]在文[6]的基础上考虑了具有利率风险的资产负债管理问题并在市场参数满足某一条件下得到了有效投资策略的解析表达式.此外,YAO等[10]研究了利率风险下的多周期资产负债管理问题并得到了有效前沿的解析表达式.

众所周知,对于具有较长投资期限的投资组合问题,通货膨胀率的大小会直接影响投资组合财富的实际价值,越高的通货膨胀率意味着财富的实际购买力水平会越低.近年来,也有不少学者研究了通胀风险背景下的投资组合选择问题.例如,Brennan和XIA[11],Munk等[12],ZHANG和Ewald[13],HAN和Hung[14],GUAN和LIANG[15],郑效晨等[16]等学者在期望效用最大化框架下利用Hamilton-Jacobi-Bellman(HJB)方法[17]或鞅方法[18]得到了相应投资组合选择问题的最优投资策略.姚海祥等[19−21]以及LIU等[22]则在均值-方差框架下利用HJB方法得到了相应投资组合选择问题有效的投资策略.需要指出的是:上述文献所建立的组合选择模型都没有考虑负债.而在实务中,投资者的投资过程往往伴随着负债.负债的引入使得所建立的模型更合符实际,但这个新增加的变量导致所建立的模型比较复杂,进而求解困难.本文的主要工作是在均值- 方差准则下研究具有利率和通胀双重风险的资产负债管理问题.在已有基于均值-方差准则研究资产负债管理的文献中,还没有学者将利率风险和通胀风险同时考虑进来.除此之外,与以往大多数文[19-22]不同,为了对冲通货膨胀风险,在投资产品中引入一种具有套期保值功能的通货膨胀指数债券(TIPS,Treasury inflation protected bonds).发行通货膨胀指数债券在西方一些国家(如美国,日本,英国,德国,加拿大和澳大利亚)和我国香港非常盛行.

2.问题描述

假设金融市场中有四个可连续交易的金融资产：无风险资产(现金),无违约的零息票债券(国债),对冲通胀风险的指数债券(TIPS)和股票.无风险资产在t时刻的价格C(t)满足如下微分方程：

其中R(t)是名义上的无风险利率且满足可匹配初始期限结构的Hull-White利率模型[21]：

这里θ0(t)是一个确定性的函数,表示名义利率的长期平均值;a0(>0)表示名义利率的均值回复速度;σR >0表示名义利率的波动水平;WR(t)是自然概率测度P下关于利率的一维标准布朗运动.

假设B(t,T)表示在到期日T支付1元的无违约零息票债券在t时刻的价格.在风险中性概率测度Q下,B(t,T)满足如下偏微分方程终值问题：

其中λR(t)是利率风险的市场价格.除此之外,B(t,T)具有如下解析表达式：

其中

在金融市场中,利率不是可交换资产.但在利率风险管理和利率衍生产品定价中,作为利率的载体-无违约零息票债券在随机利率研究中起着独特的作用.另外,正如Boulier,HUANG和Taillard[23]的研究中所讨论的,投资者很难找到到期日恰好是T的零息票债券.本文考虑一个到期日为T1的滚动债券(rolling bond)B(t,T1),为了防止T时刻套利,假定T1≥T.对(2.4)利用Itô公式,可推导出B(t,T1)满足如下随机微分方程：

众所周知,通货膨胀会影响投资者的财富,特别是对具有较长期限的投资项目(如养老金计划和社会保险基金).在金融经济中,消费者物价指数通常用来反映市场通货膨胀的水平,其变动率在一定程度上反映了通货膨胀或紧缩的程度.类似于大多数文献(如文[13,16]),假设物价指数水平I(t)满足如下随机微分方程：

其中r(t)是t时刻的实际利率.在现实中由于存在通货膨胀,实际利率可能是负的且是随机的.因此本文假定r(t)服从如下微分方程:

这里参数的金融意义见方程(2.2).除此之外,记v(t)=R(t)−r(t)+σI1λR(t)+σI2λI(t),表示物价指数水平I(t)的通货膨胀率.

金融市场的第三个资产是通货膨胀指数债券(一种特殊的零息票债券).通货膨胀指数债券的发行在西方一些国家(如美国,日本,英国,德国,加拿大和澳大利亚)和我国香港非常盛行,它被用来冲通货膨胀风险.参照文[13,16]的设置,假定通货膨胀指数债券的价格过程B(t,T2)满足如下随机微分方程：

第四个资产为风险资产(如股票),其价格过程S(t)服从几何布朗运动

其中λS(t)是风险源WS(t)的市场价格,常数σSS,σSR和σSI分别是股票价格关于WS(t),WR(t)和WI(t)的波动水平.除此之外,我们假定标准布朗运动WS(t)分别独立于WR(t)和WI(t).

定义X(t)为投资者在t时刻的总资产,πi(t),i=1,2,3分别为t时刻投资在无违约零息票债券,通货膨胀指数债券和股票的资产比例.称π(t)=(π1(t),π2(t),π3(t))T为投资者的决策过程,这里及下文出现的T表示向量或矩阵的转置.因此,在一个无摩擦可卖空的金融市场上,相应于投资策略π(t)下的总资产过程Xπ(t)可表示为

为了简便仍记Xπ(t)=X(t).由式(2.1),(2.5),(2.9)和(2.10),上式可表示为

为了简化计算,令µ1(t)=σB(t)λR(t),µ2(t)=σI1λR(t)+σI2λI(t),µ3(t)=σSSλS(t)+σSRλR(t)+σSIλI(t),σ1(t)=(σB(t),0,0),σ2(t)=(σI1,σI2,0),σ3(t)=(σSR,σSI,σSS)和W(t)=(WR(t),WI(t),WS(t))T,则式(2.11)可简化为

这里µ(t)=(µ1(t),µ2(t),µ3(t))T,σ(t)=(σ1(t);σ2(t);σ3(t))且假定σ(t)σ(t)T是可逆的.

假设投资者在投资过程中存在负债L(t),其变化过程服从如下几何布朗运动：

其中R(t)−r(t)+α(t)表示累积债务L(t)的预期增长率且是随机的,β(t)=(β1(t),β2(t),β3(t))是累积债务L(t)关于WR(t),WI(t)和WS(t)的波动水平.除此之外,假设α(t),β1(t),β2(t)和β3(t)都是连续有界的确定性函数.

在通货膨胀影响下的资产负债管理问题中,投资者关心的是剩余财富的实际价值.定义(t)=(t)(t)表示投资者在t时刻的实际财富,其中(t)=表示投资者在t时刻的实际资产,(t)=表示投资者在t时刻的实际负债.在(2.12)和(2.13)中分别利用It公式,可推导出(t)和(t)满足如下随机微分方程：

其中

在具有利率风险和通胀风险的背景下,投资者的目标是寻找到最优投资策略π∗(t),使得终端实际财富的期望E[(T)]达到最大,同时使得终端实际财富的方差Var[(T)]达到最小,即求解如下双目标优化问题：

其中Π为所有可允许策略组成的集合,即存在一个可测的随机过程f(t)使得

在均值-方差投资组合选择问题中,几乎不可能找到方差最小而均值最大的最优投资策略π∗(t),转而寻求均值-方差有效投资策略(见文[3]),即如果不存在可允许策略π(t)使得

为了得到优化问题(2.17)的有效前沿,根据文[3]的研究,可首先考虑如下方差最小的优化问题,即先固定终端实际财富的期望值使得E[(T)]=K,然后再选择可允许策略使得终端实际财富的方差Var[(T)]达到最小.更加具体地,是求解如下均值-方差有效问题：

因为

其中u=K−λ,所以最优问题(2.19)等价于

3.问题(2.20)的求解

问题(2.20)的值函数V(t,r,y,l)∈C1,2,2,2([0,T]×R×R×R+)可定义为

其中边界条件为V(T,r,y,l)=(y−u)2.除此之外,根据随机动态规划原理,V(t,r,y,l)满足如下HJB方程：

其中Vt,Vr,Vy,Vl,Vrr,Vry,Vrl,Vyy,Vyl和Vll分别是关于t,r,y和l的一阶和二阶(混合)偏导数.除此之外,记σTr=(σr1,σr2,0)T.

应用极小值的必要条件可以得到最优投资策略π∗(t)

将(3.3)代入HJB方程(3.2)并经过较为繁琐的计算后,得到如下非线性偏微分方程：

其中

方程(3.4)是一个复杂的非线性抛物型方程,在一般情况下没有解析解.但根据边界条件V(T,r,y,l)=(y−u)2,可以猜测(3.4)具有如下形式的解：

其中g(t,r)和h(t,r,l)是两个待定的函数.将(3.5)代入(3.4)并经过繁琐的计算后,得到如下等式：

消除对变量y+l−h的依赖,得到如下两个偏微分方程：

由边界条件V(T,r,y,l)=(y−u)2得到g(T,r)=1和h(T,r,l)=u+l.因此,g(t,r)和h(t,r,l)分别满足如下偏微分方程终值问题：

下面利用函数变换技巧和偏微分方程方法得到(3.9)和(3.10)的解析解,进而得到辅助问题的值函数和最优投资策略.首先求解问题(3.9).注意到(3.9)的结构类似于(2.3).因此,猜测问题(3.9)的解具有如下指数形式：

其中A1(t)和A2(t)为两个待定的函数且满足A1(T)=0以及A2(T)=0.将(3.11)代入(3.9)并整理:A1(t)和A2(t)分别满足如下两个常微分方程定解问题

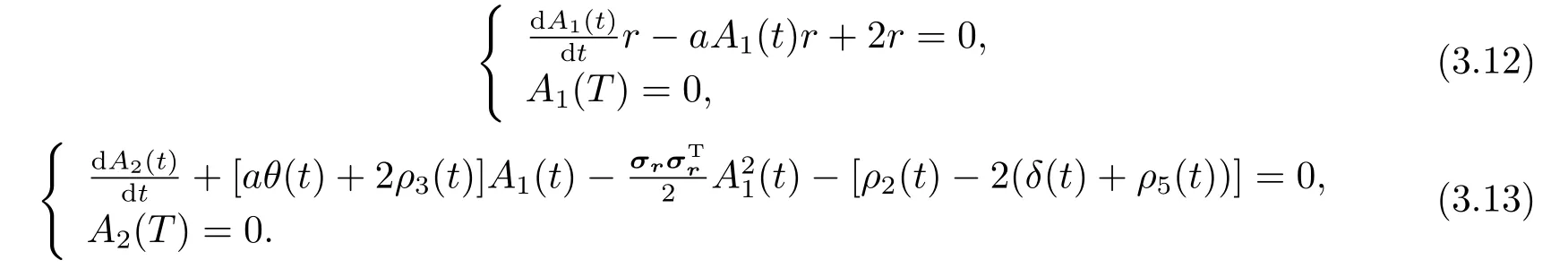
通过简单的计算后,可以得到

下面求解问题(3.10).令

其中M(t,r)=eA3(t)r+A4(t),A3(t)和A4(t)为两个待定的函数.

将(3.11)和(3.16)代入(3.10)并化简得到

由边界条件h(T,r,l)=u+l,得到M(T,r)=1和P(T,l)=u+l.因此,(3.10)可分解为如下两个偏微分方程定解问题：

完全类似于(3.9)的求解,可以得到(3.18)的解,即

其中

注意到问题(3.19)中的偏微分方程完全类似于标准的Black-Scholes方程[24],而标准的Black-Scholes方程可通过作函数变换得到解析解.为此,作自变量变换

为了得到(3.21)的解,继续作变换

通过简单的计算后,(3.21)简化为如下热传导方程的初值问题：

由Poisson公式(见文[25]),得到

返回原函数和原变量,(3.19)的解可表示为

进一步地,由(3.16),可以得到问题(3.10)的解析解，即

最后,由(3.11)和(3.25),得到优化问题(2.20)的值函数

和最优投资策略

4.原问题的有效投资策略及有效前沿

本节将根据第3节的结果以及Lagrange对偶定理[3]得到原问题的有效投资策略及有效前沿.

定义V1(0,r0,y0,l0)=infπ(t)∈ΠE[(T)−u]2−λ2表示(2.19)的值函数.根据(2.19)与(2.20)的等价性以及(3.26),可以得到

其中

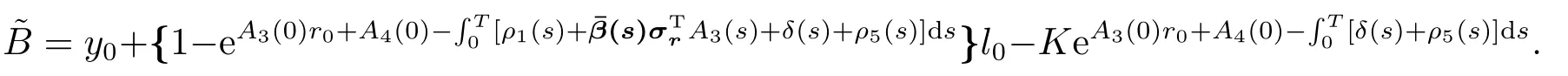
注意到(4.1)是一个关于参数λ的二次函数,而二次函数在系数满足某一条件下有最大值(或最小值).基于此,下面给出如下引理:

引理4.1如果σrA3(t)+b(t)σ(t)−1≠0,则有

证根据A1(t),A2(t),A3(t)和A4(t)的表达式,得到

因此,引理4.1得证.

引理4.1表明优化问题(2.19)最大值存在.因此,由一阶条件可得最大值点

将(4.3)代入(3.27),得到优化问题(2.19)的最优投资策略

这里u∗=K−λ∗.除此之外,可以得到(2.19)的最优值,即

来选择投资策略.至此,本文得到如下结果.

定理4.1均值-方差准则下具有利率和通胀双重风险的资产负债管理问题相对于真实终端财富期望E[(T)]=K的有效投资策略由(4.4)给出,有效前沿由(4.6)给出,其中

从式(4.4)和式(4.6)可以看出债务影响投资者的投资决策。因此,由定理4.1可以得到相应没有负债的投资策略和有效前沿，即令l0=0,(t)=0,则有

推论4.1均值-方差准则下具有利率和通胀双重风险的资产分配问题相对于真实终端财富期望E[(T)]=K的有效投资策略和有效前沿分别是

5.数值算例

本节针对本文的理论结果给出一些数值算例以分析模型主要参数对投资策略的影响.为了简化计算并不失一般性,假定所有的参数均为常数,即选择如下基本参数：

基于上面的基本参数,可以得到

下面以初始负债,利率波动和通货膨胀波动为代表讨论它们对投资策略的影响.

表5.1 初始负债对投资策略的影响

表5.2 利率波动对投资策略的影响

表5.3 通货膨胀波动对投资策略的影响

我们首先分析表5.1中的数据.随着初始负债的增大,投资在高风险资产股票的比例是逐步上升的,而投资到债券类资产(国债和通胀指数债券)的比例是下降的.这也说明在面对比较高的初始负债时,投资者在投资决策时变得比较激进.除此之外,我们需要指出的是当L0=0时,我们所考虑的模型将退化成众多学者考虑的资产分配模型(不考虑负债).除此之外,从表5.2-5.3中的数据可以看出,当σr1或σI2发生很小的波动时,投资策略需作很大的调整.

图5.1,图5.2分别给出了t=0时,有效前沿随利率波动σr1和通货膨胀波动σI2的变化图.从图5.1可以看出：当利率的波动值从σr1=0.195上升到σr1=0.21时,均值-方差有效前沿向右下方移动,即在终端真实财富方差Var[(T)]一定时,终端真实财富均值E[(T)]是减少的.图5.2显示,在终端真实财富均值E[(T)]一定的条件下,终端真实财富方差Var[(T)]对通货膨胀波动参数σI2比较敏感,如均值为4时,方差从5.629上升到6.2459.这说明通货膨胀波动参数极度影响投资边界(有效前沿).

图5.1 利率波动对有效前沿的影响

图5.2 通货膨胀波动对有效前沿的影响

6.结论

利率风险和通胀风险是投资者在投资决策过程中面临的主要背景风险.鉴于此,本文在均值-方差准则下考虑了具有利率和通胀双重风险的资产负债管理问题.利用Lagrange对偶定理,HJB方法,偏微分方程方法和一些函数变换技巧得到了此问题的有效投资策略和有效前沿的解析表达式.解析表达式为模型计算的有效性和参数估计提供了方便,是本文的主要创新点.除此之外,作为模型的直接应用,通过数值算例分析了模型主要参数对有效投资策略和有效前沿的影响.结果表明：有没有负债以及利率风险和通胀风险会对投资策略产生本质的影响.因此,本文所得结论为个体投资者以及银行,保险公司,养老保险基金等金融机构进行资产负债管理提供决策依据.