左截断数据下非线性模型的加权分位数回归
2020-01-10冯海林罗倩倩
冯海林,罗倩倩
(西安电子科技大学数学与统计学院,陕西 西安710071)
1.引言
分位数回归由Koenker和Bassett于1978年首次提出[1],是对线性回归模型的进一步拓展.随着协变量的变化,线性回归模型描述的是因变量条件均值的变化,而分位数回归模型描述的是因变量条件分位数的变化.因此,分位数回归可以比线性回归更好的展示因变量分布随协变量变化.与线性回归模型常用的最小二乘估计相比,分位数估计具有更好的稳健性(对离群值和误差分布不敏感).在误差含有异常值或者误差分布为重尾分布时,仍然可以利用分位数回归进行拟合估计.而且随着计算机的快速发展和统计软件的广泛应用,拟合分位数回归模型变得简单快捷.正是由于分位数回归具有诸多优点,近年来被广泛使用和发展.例如,YU和Jones[2]利用局部线性加权方法研究了非参数模型的分位数估计; YU和LU[3]利用相同线性加权方法讨论了可加模型的分位数估计; Honda[4]考虑了变系数模型的分位数估计;LV等[5−6]分别讨论了单指标模型和部分线性单指标模型的分位数估计等; 更多相关的研究和发展内容在YU和LU[7]对分位数回归方法的分析中可见.
上述提及的模型和方法以及结果均是基于完整数据的工作.而在很多领域的统计分析过程中,由于各种原因易导致缺失数据的产生.例如,在可靠性工程、生存分析、生物学和经济学等领域中常常出现左截断数据.左截断数据具有相同的数据结构,当研究变量小于固定的阈值或截断变量时,会造成数据缺失,无法观测到相应样本.如文[8-9]中具体给出的左截断数据实例.近年来,已经有诸多学者开始关注并研究左截断数据的统计推断问题,并取得一些成果.基于左截断数据,Bhattacharya[10]讨论了线性回归模型中斜率的非参数估计; Lynden-Bell[11]推导了截断模型下分布函数的非参数最大似然Product-Limit(PL)估计;Stute[12−13]证明了PL估计的几乎处处收敛性及中心极限定理; HE和YANG[14]讨论了随机截断模型下截断率的有效估计; HE和YANG[15]提出了左截断数据下线性回归模型的加权最小二乘估计,其中采用截断变量分布函数的PL估计定义权重.有关左截断数据的其他研究成果也可参考文[16-18]等.但是,到目前为止,只有极少部分学者利用分位数回归方法研究左截断数据.例如,ZHOU[19]研究了左截断数据下线性回归模型的加权分位数估计,其中采用与文[15]相同的权重定义方式; XU等[20]研究了左截断数据下部分线性模型的加权分位数估计.对于左截断数据下非线性模型的分位数估计,至今几乎没有研究结果.
本文的主要工作是拓展了文[19-20]针对左截断数据的分位数回归的相关工作.即针对左截断数据,建立了非线性模型的加权分位数估计,其中权重定义方式与文[15]保持一致.并在一定的假设条件下,给出了估计的大样本性质及其相关结论的理论证明.进一步,使用蒙特卡罗方法验证所提估计的有效性和真实性.
2.分位数估计及主要定理
对任意分位点τ ∈[0,1],本文考虑左截断数据下非线性回归模型:

其中,Y为因变量,X为协变量,f(·,β(τ))为p维参数向量β(τ)的已知函数,ε(τ)为满足等式P(ε(τ)≤0| X)=τ的随机误差.需要注意的是ε(τ)可能存在异方差.在左截断模型下,变量(Y,X)被随机变量T截断.当且仅当Y ≥T时,才可以观察到(Y,X,T)的样本,若Y < T,则无法观察到任何样本值.
记 {(Yi,Xi,Ti),1≤i ≤N}为独立同分布于变量(Y,X,T)的完整样本.在截断变量T影响下,仅仅可观察到变量(Y,X,T)的部分样本:

令P和E分别表示N-样本下的概率测度和期望,P和E表示n-样本下的概率测度和期望.α=P(Y ≥T)表示随机变量Y可观察的概率,又称为截断率.当α=0 时无法观察到变量(Y,X,T)的任何样本,所以本文通篇假设α>0.
Ⅰ非参数估计
定义

其中分布函数F(y)的定义域记为(aF,bF):aF=inf {y:F(y)>0},bF=sup {y:F(y)<1},可类比定义分布函数G(t)的定义域(aG,bG).
这里,将分布函数右上角标*表示n-样本下的分布函数,由文[15]可知

相应经验估计函数为

令


若Y和T的样本无节点,上述估计式可简化为

实际上,当样本没有被截断时,PL估计就退化为经验分布估计.又由C(y)=α−1G(y)[1−F(y−)],可得α的非参数估计式为

由文[15]可知,αn的取值与y无关,可以由任意一个满足条件Cn(y)=0的y计算取值.因此,从上述一系列的推导中可得到F(y,x)的非参数估计式

Ⅱ加权分位数估计
对于任意分位点τ ∈(0,1),非线性回归模型(2.1)的分位数估计定义为

其中QY(τ|X)=inf {y:P(Y ≤y|X)≥τ}表示Y在特定X取值下第τ条件分位数,随机误差满足条件P(ε(τ)≤0|X)=τ.
在完整数据N-样本下,上述分位数估计损失函数为

其中ρτ(u)=u(τ−I(u <0)),也可以写为为(Y,X)的经验估计函数.在左截断模型下,利用前面推导的F(y,x)的非参数估计式Fn(y,x)代替(y,x),得到


当样本不存在截断时,对于任意的i,Gn(Yi)=1,上式即为一般分位数回归的损失函数.
Ⅲ一致性与渐近正态性
在给出所提估计的大样本性质之前,需要做如下假设:
(A1)分布函数F和G连续且满足aG (A2)随机误差ε在给定X取值时具有条件分布函数Fε(·|X)和条件密度函数fε(·|X).其中对于任意的X,Fε(0|X)=τ,fε(e|X)在零领域(−δ,δ)内连续; (A3)E[(∇f(Xi,β∗))⊗2]=Γn,其中0<Γn <∞,E[(∇f(Xi,β∗))⊗2]=E[∇f(Xi,β∗)∇f(Xi,β∗)T]; 假设(A1)是为了保证F(y)=P(Y ≤y|Y ≥aG)和G(t)=P(T ≤t|T ≤bF)成立.(A2)使得随机误差满足分位数回归模型假设条件P(ε(τ)≤0|X)=τ.假设(A3)-(A4)为定理证明需要. 定理1(一致性)在假设(A1)-(A4)成立的条件下,令β∗(τ)为β(τ)的真实值,则有 定理2(渐近正态性)在假设(A1)-(A4)成立的条件下,则有 其中Σ的定义见第四节中定理证明过程. 为了验证所提出方法的有限样本性质,利用蒙特卡罗方法考虑如下指数回归模型 其中参数β0=1,β1=2,协变量X∼U(0,1),截断变量T服从均值为c,方差为d的正态分布,ε为随机误差.通过调整c和d的取值确定不同样本截断率.为了检验方法的稳健性,考虑了三种不同的误差分布,并以偏差和标准差作为衡量方法优劣的主要指标. 例1ε∼N(0,1). 例2ε=X∗e,其中e服从均值为0,方差为2∧2的正态分布. 例3ε∼t(3). 由前面加权分位数估计的定义可知,权重在最小化目标函数中占有重要的作用,其非参数估计主要取决于分布函数F(y)和G(t)的PL估计Fn(y)和Gn(t).因此在进行参数估计之前,首先对Fn(y)和Gn(t)的拟合效果进行检验.针对分布函数F(y)和G(t),现将τ=0.5 时左截断数据(截断率25%)下的PL估计(PL)和完整数据下的经验估计(ECDF)展示于图1-3. 图1 N(0,1) 图2 X∗e 图3 t(3) 可以看出,PL估计与ECDF估计分布相一致且不受误差影响,这一结果对于后续的参数估计至关重要. 注3.1分布函数F(y)和G(t)的PL估计主要取决于Cn(·).但在随机截断模型下,Cn(·)的取值有可能趋于0,这将会导致Fn(y)和Gn(t)估计的不合理性.因此在仿真计算中,采用C∗n(y)代替Cn(·): 该方法由Woodroofet[8]首次提出,并且Stute和WANG[13]证明了基于C∗n(y)的估计与基于Cn(·)的估计相比,估计结果等价. 注3.2为了满足分位数回归假设条件P(ε(τ)≤0|X)=τ,在计算中对随机误差进行略微调整,令εi−Qε(τ)→εi,其中Qε(τ)表示误差ε的第τ分位数. 现在进行参数估计.首先从变量(Y,X,T)中随机产生300组样本量均为100的随机样本.通过调整c和d的取值考虑约10%,25%,60%三种样本截断率.同时在每种截断率下,分别考虑τ=0.25,0.5,0.75三种分位点下的加权分位数估计.各误差分布下的回归参数估计结果见表1-3. 表1 β0,β1估计结果, ε∼N(0,1) 表2 β0,β1估计结果, ε=Xe, e∼N(0,4) 表3 β0,β1估计结果, ε∼t(3) 表4 OMNI,WQR和LS三种估计方法对比 从表1-3中可以看出,在指数回归模型的三种误差分布下,加权分位数估计均具有较小的偏差和标准差.且随着截断率的增加,加权分位数估计的偏差和标准差呈现递增趋势.同时,为体现方法的优越性,在τ=0.5分位点时,将完整数据下分位数估计(OMNI)、左截断数据下加权分位数估计(WQR)、左截断数据下最小二乘估计(LS)三种估计方法进行对比并将结果展示在表4中. 当随机误差服从正态分布时,LS的估计效果优于WQR,仅次于OMNI估计.但当误差服从其他分布时,WQR 估计的偏差,标准差均小于相应的LS 估计,WQR估计效果明显优于LS 估计.上述现象源于,最小二乘估计稳健性较差,在随机误差服从异方差和分布时,最小二乘估计不再具有好的性质.而分位数估计具有强稳健型,对异常值不敏感,因而具有更强的优越性. 引理1[13]如果分布函数F和G连续且满足 对于x ∈(aG,bF),则有 其中Wi(x)=为均值为0,方差为的独立同分布随机变量. 定理1,2的证明令un=则un最小化下列等式 由fXi,β∗(τ)+n−1/2un在处的泰勒展开式 及等式ρτ(r−s)−ρτ(r)=s[I(r <0)−τ]+0s[I(r ≤x)−I(r ≤0)]dx, 其中∇f(Xi,β∗(τ))=[∂f(Xi,β(τ))/∂β(τ)]|β(τ)=β∗(τ), 首先计算In1,定义zn1=则 由Cramér-Wald定理和中心极限定理,则有 其中W1为均值为0的p维正态随机向量.接下来计算In2. 相似的可以计算Var(In2)=op(1),从而有 最后计算In3,由引理1可知 定义 由鞅的中心极限定理,可以证明zn2→W2,其中W2为均值为0的p维正态随机向量,因此 结合(5.1),(5.2)和(5.3)可得 当||un||足够大时,由(W1+W2)Tun=Op(||un||),则Qn主要由正则项决定.因此对任意的δ >0,存在常数C,当n充分大时,有 又由最小化Qn的un应满足 本文主要研究了左截断数据下非线性模型的加权分位数回归,采用截断变量T的PL估计定义权重.并在一定假设条件下,给出了加权分位数估计的大样本性质.利用数值模拟展示了方法的有效性,并将方法与最小二乘回归进行对比.对比结果显示,当随机误差不服从正态分布时,所提方法与最小二乘估计相比可以更准确的估计模型参数.


3.数值仿真









4.定理的证明




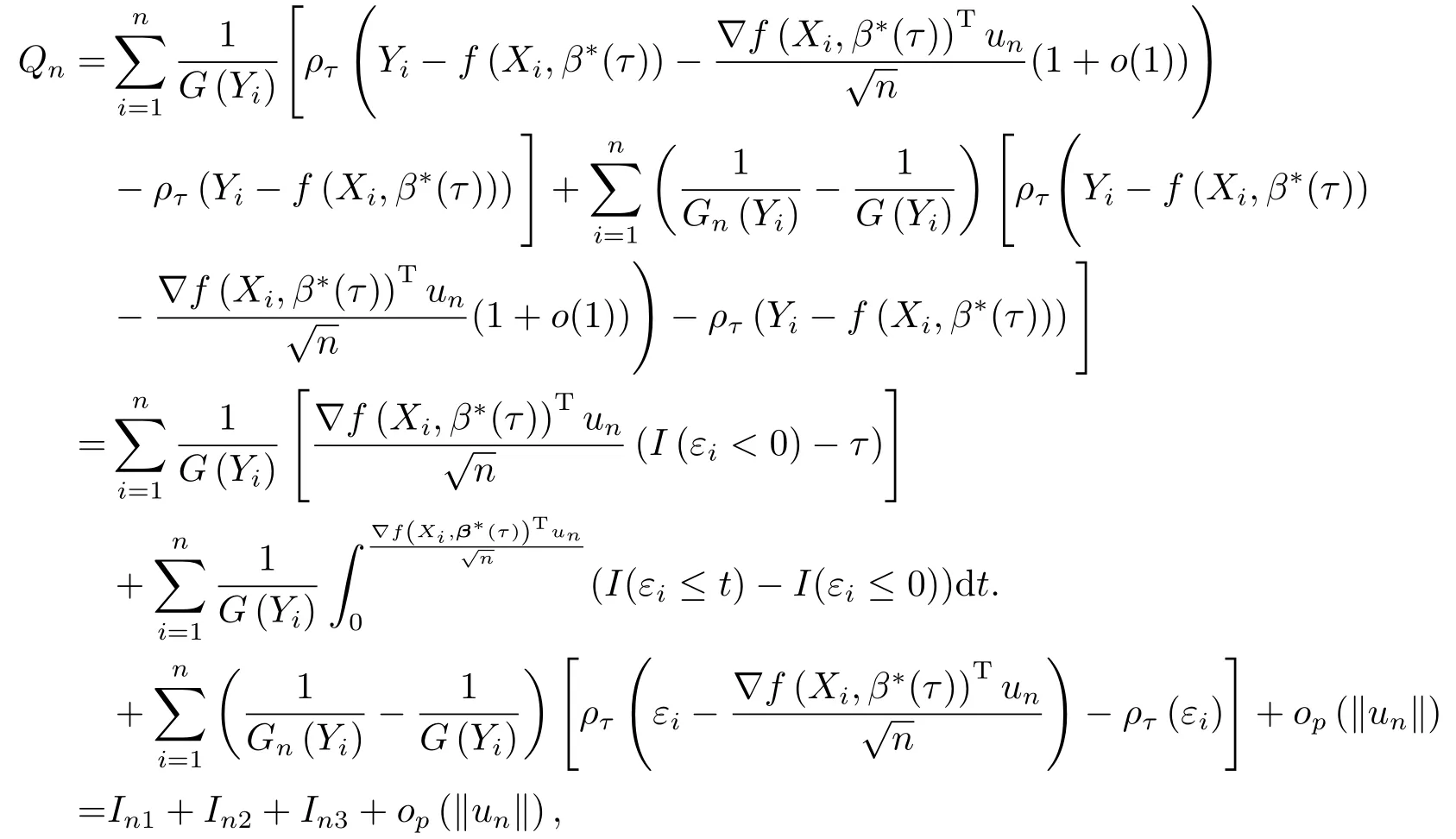












5.结语
