含多调和延拓算子的积分方程组的Liouville型定理
2020-01-10唐素芳
唐素芳
( 西安财经大学统计学院,陕西 西安710100)
1.引言
令Rn+={x=(x1,x2,...,xn)∈Rn | xn >0}是上半欧氏空间.对x ∈Rn+,y ∈∂Rn+=Rn−1,2−n 为上半空间的Poisson核.对定义在∂Rn+上的函数f,多调和延拓算子定义为: 2014年,CHEN[1]证明了上半空间一类带边界项的精确的积分不等式: 其中1< p ≤∞,n ≥2.并且,当p=时,他还证明了不等式的极值函数的存在性.2008年,在a=0的情形下,HANG等[2]建立了不等式(1.1),并利用移动平面法对不等式的极值函数进行了分类. 不等式(1.1)对应的Euler-Lagrange 方程为 为了得到这个方程解的存在性,CHEN[1]采用了重排不等式和文[2]中的命题4.1来证明. 若记u(x)=(Paf)(x),v(y)=fp−1(y)及κ=则可把上面的Euler-Lagrange方程写成如下的积分方程组:注意到此积分方程组在临界指数的情形下关于Kelvin变换满足共形不变性,因此我们在文[3]中在临界指数的情形下对方程组(1.2)的正解进行了分类,在次临界指数的情形下证明了正解的不存在性. 受上述工作的启发,本文考虑如下更一般的积分方程组: 其中f,g:[0,∞)→[0,∞)是非负的连续函数,且满足如下条件: (i)f(t),g(s)在(0,∞)上非减; (ii)F(t)=上非增,这里 本文的主要结果如下. 定理1.1假设f,g:[0,∞)→[0,∞)是非负函数且满足条件(i)和(ii).若(u,v)是方程组(1.3)非负解,且满足: 其中a1,a2>0,d>0,η0∈∂Rn+. 当a=0时,DOU和ZHANG在文[4]中同样利用积分形式的移动球面法证明了方程组(1.3)的Li-ouville型定理.特别地,若a=0及f(v)=vκ,g(u)=uθ时,方程组(1.3)恰好是文[2]中的积分不等式的极值函数满足的Euler-Lagrange方程的变形. 近年来,一些研究者考虑了含调和核的积分方程组: 其中1< α < n.该方程组的正解与Hardy-Littlewood-Sobolev (HLS)不等式的极值函数密切相关.在f,g满足类似于(i)和(ii)的某些自然结构条件下,YU[5]利用移动平面法讨论了方程组(1.4)的Liouville型定理.当f(v)=vq及g(u)=up时,CHEN等[6−7]和HANG[8]分别在不同的指数条件下利用积分形式的移动平面法证明了方程组(1.4)解的径向对称性和单调性等性质.特别地,当u=v及p=q=时,方程组(1.4)归结为单个方程,CHEN等[9]和LI[10]分别利用积分形式的移动平面法和积分形式的移动球面法对方程的正解进行分类. 同样地,上半空间含调和核的积分方程组为: 其中1< α < n.注意到,当f(v)=及g(u)=时,DOU和ZHU[11]证明了方程组(1.5)恰好是上半空间相应于HLS不等式的Euler-Lagrange方程,并利用积分形式的移动球面法及Li-Zhu引理[12],对该方程组的正解进行了分类.此外,DOU和LI[13]考虑了方程组(1.5)的Liouville型定理,且f,g满足类似于(i)和(ii)的某些自然结构条件. 若f(v(y))=vκ(y),g(u(x))=uθ(x),κ=则方程组(1.3)关于Kelvin变换具有共形不变性.因此,本文也采用积分形式的移动球面法对方程组的正解进行分类.此外,由于指数κ<1,所以在处理不等式的时候需要不同的估计技巧. 本文组织如下:第2节介绍本文要用到的一些记号和相关引理.第3节利用积分形式的移动球面法证明定理1.1. 首先介绍一些本文要用到的记号.对于R>0,记 当x=0时,记BR=BR(0),Bn−1R=Bn−1R(0),B+R=B+R(0),ΣnR=Σn0,R,Σn−1R=Σn−10,R . 下面定义(1.1)式的对偶形式.令g是定义在Rn+上的函数,记Pa的对偶算子为: 命题2.1[3]令1≤p 其中g ∈Lp(Rn+). 为了证明定理1.1,需要利用下面的正则性结果. 命题2.2设κ>0,1≤θ ≤−1,f,g:[0,∞)→[0,∞)是非负的连续函数且满足条件(ii).令(u,v)是方程组(1.3)的一组正解,且(∂Rn+),假设 成立,其中κ0=那么可推出v ∈C∞(∂Rn+),u ∈C∞(Rn+). 这个关于正则性的命题的证明,可类似于文[3]中的定理2.3或文[4]中的定理2.3推得,此处略. 本文还需要下面三个关键引理,这三个引理在移动球面的过程中至关重要.第一个引理和第二个引理由文[10]给出,并且在更强假设下的结论由LI,ZHU[12]及LI,ZHANG[14]给出.第三个引理由DOU和ZHU在文[11]中给出,它把文[10]中的结果推广到了上半空间. 引理2.1[10]对n ≥1及µ∈R,若f是定义在Rn上的实值函数且满足: 则f(x)=C是常函数. 引理2.2[10]令n ≥1,µ∈R,及f ∈C0(Rn).假设对任意的x ∈Rn,存在λ>0使得 那么,存在a ≥0,d>0及∈Rn,使得 引理2.3[11]对n ≥1 及µ∈R,若f是定义在Rn+上的实值函数且满足: 则我们有 本节利用积分形式的移动球面法证明定理1.1.为方便使用移动球面法,定义变换: 其中λ>0,ξ ∈Rn+{x},η ∈∂Rn+{x},及 分别是ξ和η关于球Bλ(x)和(x)的Kelvin变换.简记ωkx,λ(ξ):=(ωx,λ(ξ))k. 现在证明下面几个引理. 引理3.1令(u,v)是方程组(1.3)的一组正解,则有 其中x ∈∂Rn+.并且,有 这里 可推出P1(x,λ;ξ,η)>0,P2(x,λ;η,ξ)>0,对任意的0. 证这个引理的证明过程类似于文[3-4,10-11]中相应引理的证明,但是我们需要更繁琐的计算.为方便起见,记 其中x ∈∂Rn+,λ>0.那么有 令y=ηx,λ,则有 并且,根据第n个变量的Kelvin变换有 则有 同理,可得 同理可证(3.2)式成立.将ux,λ(ξ)与u(ξ)相减,可得 注意到 及 将上面两个式子相减后,再带入到(3.5)式中,可得(3.3)式.同理,可推出(3.4)式成立. 类似于文[13]中的证明,可证得P1(x,λ;ξ,η)>0,P2(x,λ;ξ,η)>0,其中及λ>0. 为下文叙述方便,记 引理3.2在假设(H′)成立的条件下,令(u,v)是方程组(1.3)的一组正解,则对任意的x ∈∂Rn+,存在λ0(x)>0使得对任意的0<λ<λ0(x),有 证当时,显然有v(ηx,λ)≥vx,λ(η),根据条件(ii)可知F(v(ηx,λ))≤F(vx,λ(η)).另一方面,根据条件(i)可知对有f(vx,λ(η))≤f(v(η)).从(3.3)可知,对有 上式用到了中值定理,且r ∈[,θ].令f+(x)=:max {f(x),0},及s>则从(1.1)式及Hölder不等式有 其中()C是的余集, 根据引理3.1的推导过程,有 另一方面,我们有 HANG在文[8]中证明了基本不等式: 其中0< s ≤1,a ≥b >0及c ≥0.类似于文[15]中的方法,对η ∈Σvx,λ,从(3.7)式,(3.8)式及(3.9)式,推出 从(2.1)式推出 在(H′)的假设条件下,存在充分小的λ0使得对0<λ<λ0,有 将上式带入到(3.12)式中,有 令 引理3.3对某个x0∈∂Rn+,若=:(x0)<∞,则 证这个引理的证明思路与文[11]中的引理3.4或文[3]中的引理3.3的证明思路类似.根据的定义,有 从(3.3)式及(3.4)式推出,对λ ∈[,+ε),存在充分小的ϵ<δ使得 这表明 记 当R→∞时,ε1=λ/R任意小.令 分别为和在Kelvin 变换下关于球 {x:|x−x0|=λ}的反射.类似于(3.12)式的推导,有 根据假设(H),∫ 有 选取充分小的ε0,使得对λ ∈[,+ε)有 类似地,有 其中λ ∈[,+ε),这与的定义矛盾.从而引理3.3得证. 定理1.1的证明情形1 若存在某个x0∈∂Rn+使得(x0)< ∞,则类似于文[16]中的引理4.2的证明过程可以表明(x)<∞,∀x ∈∂Rn+.再根据引理3.3有 从引理2.2推出 这里a1,d>0及η0∈∂Rn+. 将上式带入到方程组(1.2)的第一个方程中,并类似于文[10]中引理6.1的证明过程,有 其中a2,d>0. 情形2 若对任意的x ∈∂Rn+都有(x)≡∞,那么有 从引理2.1可推出v >0是一个常函数.另一方面, 根据引理2.3可知u只与变量t有关.因此,有 显然,u(0,t)不依赖于变量t.因此,u也是一个常函数.定理1.1得证.









2.预备引理









3.定理1.1的证明


























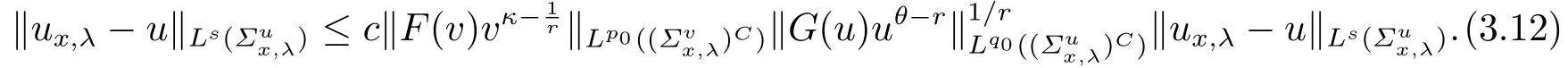








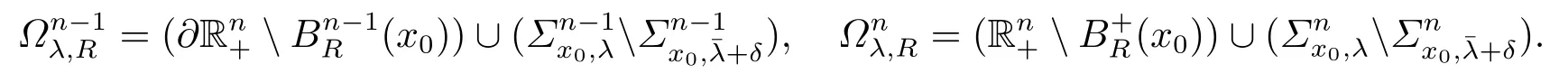












猜你喜欢
杂志排行
应用数学的其它文章
- Threshold Dynamics of Discrete HIV Virus Model with Therapy
- Solvability for Fractional p-Laplacian Differential Equation with Integral Boundary Conditions at Resonance on Infinite Interval
- Long-Time Dynamics of Solutions for a Class of Coupling Beam Equations with Nonlinear Boundary Conditions
- Existence and Uniqueness of Mild Solutions for Nonlinear Fractional Integro-Differential Evolution Equations
- 基于Markov链的税延型养老保险跨期效用
- 动态投资组合现金次可加风险度量的时间相容性
