部分线性模型的模态正交经验似然推断
2020-01-10陈健赵培信
陈健,赵培信,2
(1.重庆工商大学数学与统计学院,重庆400067;2.经济社会应用统计重庆市重点实验室,重庆400067)
1.引言
进行回归分析时,如果模型误差服从正态分布,那么普通最小二乘估计是一个有效的模型估计方法.但是,如果模型误差不服从正态分布,特别是当模型误差为厚尾分布或数据含有异常点时,普通最小二乘估计则不再是一个有效的统计推断方法.随着社会的发展和科技的进步,实际问题中遇到的数据结构越来越复杂.在统计建模时,假定模型误差分布服从正态分布或者不含有异常点,往往是不切实际的.因此,关于模型的稳健统计推断问题越来越受到关注,并且许多文献已提出大量的稳健统计推断方法,其中模态回归(modal regression)方法[1]是一种既具有较好的稳健性,又保留了估计的有效性的稳健统计推断方法.具体地,记f(y|x)为给定协变量X的情况下响应变量Y的条件密度函数,YAO和LI[1]定义f(y|x)的模为Mode(Y|X)=arg maxy(f(y|x)),对线性回归模型Yi=XTi β+εi,i=1,2,··· ,n,提出参数β的模态估计为最大化如下目标函数的解.
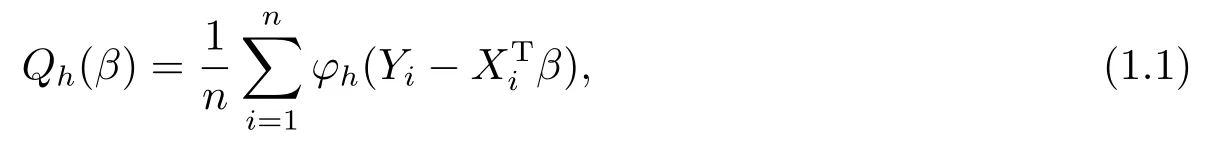
其中φh(·)=h−1φ(·/h),φ(·)为对称的核函数,h为带宽.
目前,已有大量的文献对模态估计相关理论和应用进行了研究.比如YAO等[2]对非参数回归模型提出了一个局部模态估计方法.LIU等[3]利用模态估计方法研究了单指标模型的统计推断问题.YANG等[4]利用模态估计方法研究了部分线性单指标模型的估计问题.LV等[5]结合模态估计方法研究了非线性模型的变量选择问题.ZHANG等[6]则基于模态估计方法研究了部分线性变系数模型的变量选择问题.
另外,在模型参数估计以及检验方面,经验似然方法[7]是一种有效的非参数统计推断方法.该方法在构造参数置信区间方面具有许多优良的性质,比如避免了极限方差的估计,并且置信域的形状完全由数据确定等.目前经验似然方法广泛应用到参数模型,非参数模型以及半参数模型的统计推断中.ZHAO等[8]结合模态估计方法对线性回归模型,提出了一个基于模态估计的经验似然统计推断过程.但是在实际问题建模中,线性回归模型往往不能有效刻画数据间的相关结构,而部分线性模型是线性模型的一个有效的推广形式.为此,本文将结合模态估计技术,研究部分线性模型的模态经验似然统计推断问题.具体地,考虑如下部分线性模型

其中β=(β1,··· ,βp)T为p维的未知参数向量,g(·)为未知非参数函数,Xi为p维协变量,Ui为1维协变量,Yi为响应变量,εi为零均值的模型误差.另外,不失一般性,本文假定Ui在区间[0,1]上取值.
接下来,本文结合模态估计方法和正交投影技术,对模型(1.2)提出了一个模态经验似然统计推断过程.并且证明了所构造的经验对数似然比函数渐近服从中心卡方分布,进而给出了模型参数的置信区间估计.本文通过正交投影技术,使得所提出的估计过程可以分别对模型的参数分量β和非参数分量g(·)进行估计,而互不影响.因此,与已有估计方法相比,本文所构造的置信域同时具有较好的稳健性和有效性,并且在实际应用中更加容易计算.最后通过一些数据模拟结果说明该方法是行之有效的.
2.方法论及主要结果
我们首先利用B样条逼近技术[9]来逼近非参数函数g(u).设B(u)=(B1(u),··· ,BL(u))T阶数为M的B样条基函数,其中L=K+M,K为内部结点个数.那么g(u)可以渐近表示为g(u)≈B(u)Tγ,其中γ为基函数系数.进而结合模型(1.2)可得
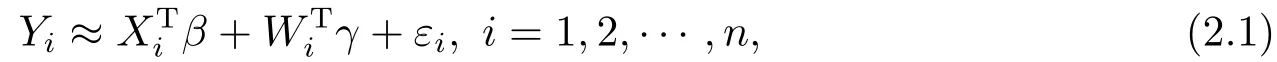
其中Wi=B(Ui)=(B1(Ui),··· ,BL(Ui))T.记X=(X1,··· ,Xn)T,W=(W1,··· ,Wn)T,Y=(Y1,··· ,Yn)T,ε=(ε1,··· ,εn)T,则模型(2.1)可写为

假定W为n×L的列满秩矩阵,那么利用矩阵的QR分解公式可得
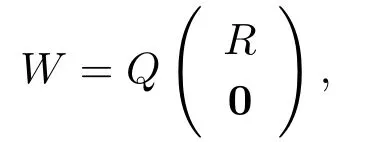
其中Q是一个n×n正交矩阵,R是一个L×L上三角矩阵,0是一个(n−L)×L零矩阵.进一步,对Q进行分块为Q=(Q1,Q2),其中Q1为n×L矩阵,Q2为n×(n−L)矩阵.那么有W=Q1R以及QT2Q1=0.因此可得QT2W=QT2Q1R=0.进而在(2.2)式两边同时乘以QT2可得

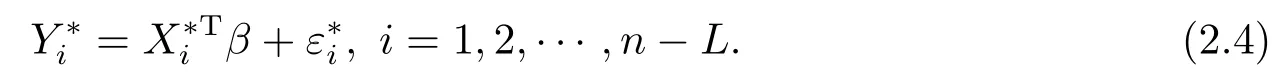
注意到模型(2.4)为一个仅含有参数分量的标准线性回归模型,因此为构造参数β的模态经验似然比函数,类似文[8],定义辅助随机向量
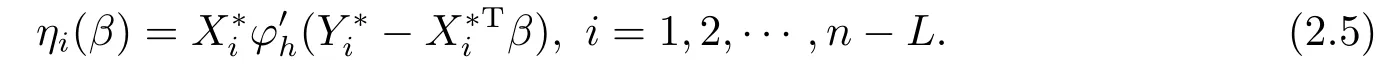
并进一步定义关于β的经验对数似然比为
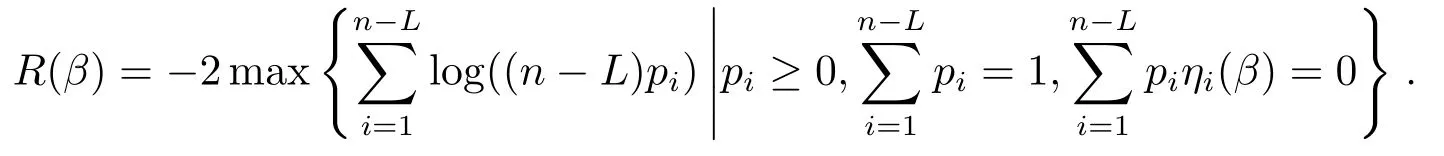
接下来,我们给出R(β)渐近分布.为此首先罗列一些渐近结果所需要的正则性条件.
(C1)非参数函数g(u)为r阶连续可微函数,这里r ≥2;
(C2)模型误差ε满足E(ε|X,U)=0,并且存在一个正常数δ >0,使得E(|ε|2+δ)<∞;
(C3)设c1,··· ,cK为区间[0,1]的内部节点,并记c0=0,cK+1=1以及∆i=ci−ci−1.那么存在常数C0使得max {∆i}/min {∆i}≤C0和max {|∆i+1−∆i|}=o(K−1);
(C4)对任意给定的带宽h,核函数φh(·)满足E(φ′h(ε))=0,Fh ≡E(φ′′h(ε))>0 以及Gh ≡E(φ′h(ε)2)<∞;
(C5)记Σ=E {φ′h(ε∗i)2X∗i X∗Ti}和Γ=E {φ′′h(ε∗i)X∗i X∗Ti},那么Γ和Σ均为可逆矩阵.在这些正则条件下,如下定理给出了R(β)的渐近分布.
定理2.1假设正则条件(C1)-(C5)成立,并且内部节点个数K满足K=O(n1/(2r+1)).那么当n→∞时,有R(β)2p,其中表示以分布收敛,χ2p表示自由度为p的中心卡方分布.
记χ2p(1−α)为χ2p的1−α分位点,那么由定理2.1可知β的1−α置信区间可定义为Cα(β)= {β|R(β)≤χ2p(1−α)}.另外,最大化 {−R(β)}则得到β的最大经验似然估计,记为.在一些正则条件下,如下定理2.2表明渐近服从正态分布.
定理2.2假设正则条件(C1)-(C5)成立,并且内部节点个数K满足K=O(n1/(2r+1)).那么当n→∞时,有其中Σ和Γ由条件(C5)所定义.
接下来,我们给出非参数分量g(u)的估计过程.把参数分量β的经验似然估计代入模型(2.1)可得=WTi γ+εi,其中=Yi−.进而,类似参数分量β的估计过程,定义辅助随机向量ψi(γ)=Wiφ′h(−WTi γ),i=1,2,··· ,n,并进一步定义关于γ的经验对数似然比为

定理2.3假设正则条件(C1)-(C5)成立,并且内部节点个数K满足K=O(n1/(2r+1)).那么当n→∞时,有其中||·||表示函数的L2范数.
另外,在实际应用中内部节点个数K以及带宽h需要选择.类似文[8],我们给出一个关于K和h的选择方法.定义和其中那么K和h的估计定义为

尽管基于该方法给出的参数在理论上可能不是最优的,但第4节的数据模拟结果表明该选择方法是可行的.
3.定理的证明
引理3.1设ξi,i=1,··· ,n,为相互独立的随机变量序列,且满足E(ξi)=0 和E(ξ2i) 证参见文[9]中引理A.2的证明. 引理3.2假定条件(C1)-(C5)成立,那么当β为参数真值时,有 其中Σ由条件(C5)所定义. 证记R(Ui)=g(Ui)−B(Ui)Tγ和R(U)=(R(U1),··· ,R(Un))T,结合QT2W=0 可知 记QT2R(U)=(r∗1(U),··· ,r∗n−L(U))T,那么结合(3.1)式以及ηi(β)的定义可知 注意到E(Jn1)=0以及Var(Jn1)=Σ,因此由中心极限定理可知 另外由条件(C1),(C3)以及文[10]的推论6.21可得||R(U)||=O(K−r).进而结合引理3.1,简单计算可得Jn2=Op((n−L)−1/2(n−L)1/2log(n−L)K−r)=op(1)和Op((n−L)1/2||R(U)||2)=op(1).因此结合(3.2)和(3.3)式,并利用Slutsky定理则完成了本引理的证明. 定理2.1的证明结合ηi(β)的定义,并利用类似文[7]的证明可得 进而结合(3.4)和(3.5),并利用类似文[11]中定理4证明方法可得 定理2.2的证明结合(3.6)式并用类似文[11]的证明可知,最大经验似然估计为估计方程的解.因此有 另外利用Taylor展开可得 结合(3.7)和(3.8)式,简单计算可得 利用大数定律可得 因此,结合(3.9),(3.10)式以及引理3.2的证明过程,并利用Slutsky定理可得N(0,Γ−1ΣΓ−1).这就完成了定理2.2的证明. 定理2.3的证明类似定理2.2的证明可知,γ最大似然估计为的解.进而为最小化如下目标函数Qh(γ)的解 记τ=n−r/(2r+1)和γ=γ0+τξ,其中γ0表示γ的参数真值.我们首先证明对任意给定的ϵ >0,那么存在常数C使得 利用Taylor展开,并经简单计算可得 记∆(γ)=K−1[Qh(γ)−Qh(γ0)],结合(3.14)和(3.15)式可得 注意到K=Op(n1/(2r+1)),进而有Op(nτ2K−1)=Op(1),并且Op(n1/2τK−1)和op(nτ2K−1)均为op(1).因此,对充分大的C,J2和J3均一致小于J1.另外由J1恒为正值可得(3.12)式成立.即以概率1−ε存在极小值点满足 另外由简单计算可得 由||R(u)||=O(K−r)和K=Op(n1/(2r+1))可知进而结合(3.17)和(3.18)式可得这就完成了定理2.3的证明. 在这一节,我们通过一些数值模拟来说明本文提出估计方法的有限样本性质.我们基于如下模型产生数据Yi=Xiβ+g(Ui)+0.5εi,i=1,··· ,n,其中取β=2以及g(u)=cos(2πu).为实施模拟,取协变量Xi∼N(1,2),Ui∼U(0,1),响应变量Yi根据模型产生,其中模型误差εi分别取为正态分布N(0,1),自由度为3的t分布t(3)以及拉普拉斯分布La(0,1)三种情况来代表不同的模型误差形式.在模拟过程中取三次B样条基函数对非参数分量进行展开,并利用高斯核函数进行模态回归,其中内部节点个数K以及带宽h通过(2.6)式进行选择.另外,在模拟过程中样本容量分别取为n=50,100和150三种情况,并且对每一种情况,实验重复1000次. 对参数分量β,我们对三种方法进行比较:模态经验似然方法(基于定理2.1),记为MR-EL;模态回归估计的正态逼近方法(基于定理2.2),记为MR-NA; 以及经典的最小二乘估计的正态逼近方法,记为LS-NA.表4.1给出了基于1000次重复实验,参数分量β的95%置信区间的平均长度(AL)以及对应的覆盖概率(CP).由表4.1,我们可以得到如下结论: (i)对任一给定的模型误差,基于本文提出的模态经验似然方法(MR-EL)给出的置信区间随着样本量的增加,区间长度则逐渐变短,并且对应的覆盖概率越来越接近名誉水平0.95.这表明本文提出的模态经验似然方法是行之有效的. (ii)当模型误差为正态分布时,基于三种方法给出的模拟结果是类似的.但当模型误差为非正态分布时,本文提出的模态经验似然方法(MR-EL)明显优于最小二乘方法估计方法(LS-NA).这就表明本文提出的模态经验似然方法是相对稳健的. (iii)与MR-NA方法相比,MR-EL给出了稍微较短的置信区间.这主要是因为基于MREL方法的置信区间构造过程不涉及任何渐近方差的估计,而基于MR-NA方法的置信区间构造过程需要给出估计量渐近方差的估计,从而影响了置信区间的精度. 表4.1 基于不同的估计方法,对参数分量β的模拟结果. 图4.1 基于MR-EL方法, g(u)的估计曲线 另外对非参数分量g(u),如图4.1给出了当n=100,ε∼t(3)时,基于本文提出的模态经验似然方法给出的估计结果,其中虚线表示估计曲线,实线为真实曲线.从图4.1可以看出对非参数分量的估计,本文提出的模态经验似然方法仍然是行之有效的.在样本容量及模型误差为其他情况下的模拟结果与图4.1是类似的,由于篇幅所限,本文不一一展示.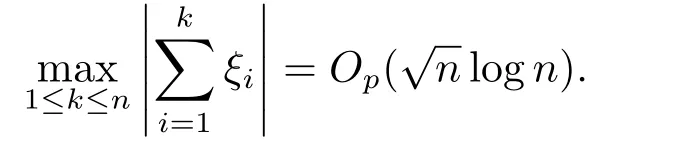
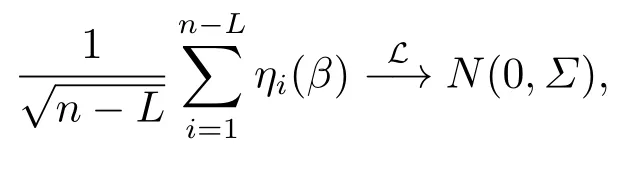
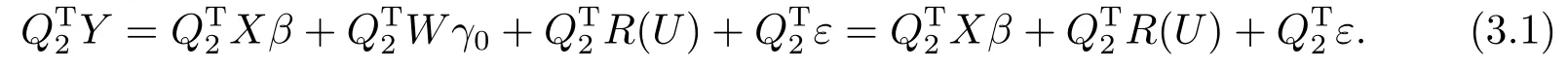
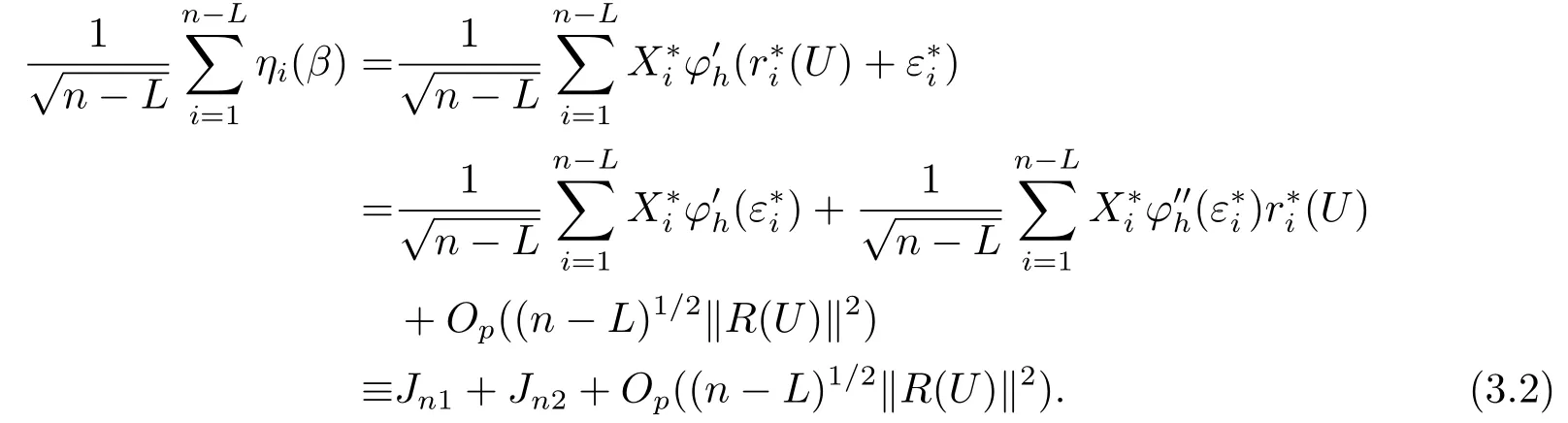

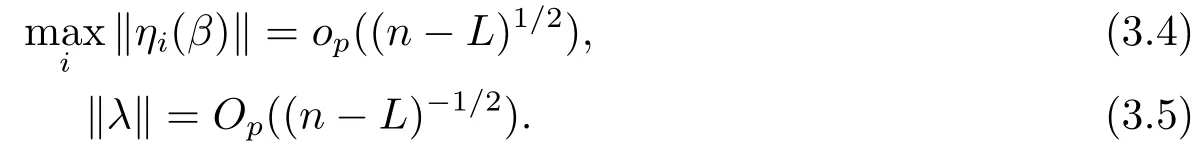
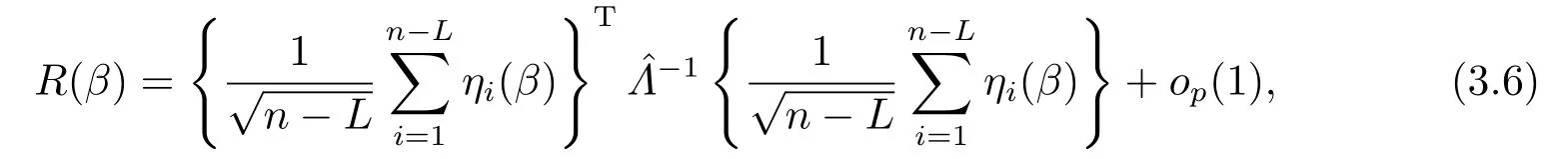
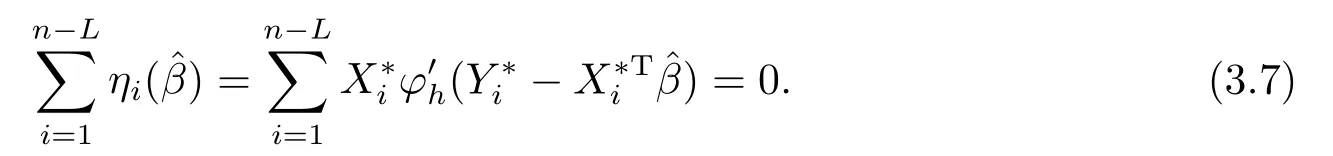
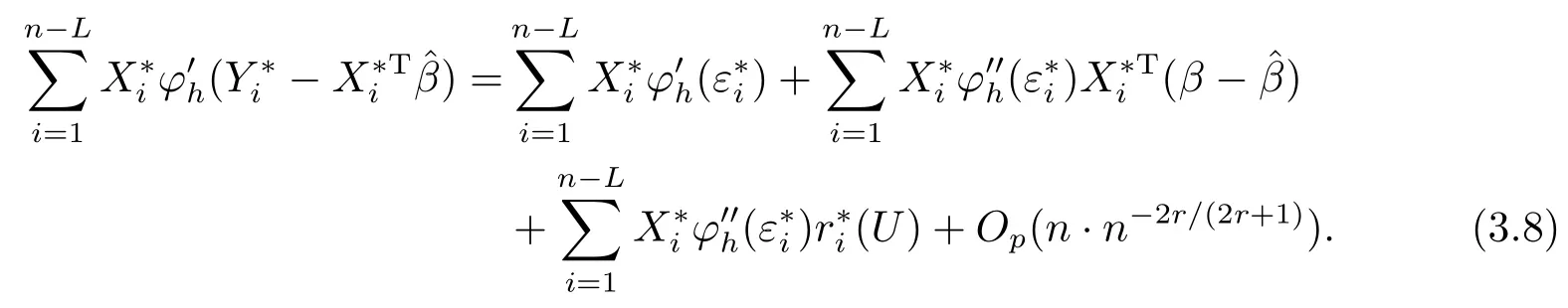
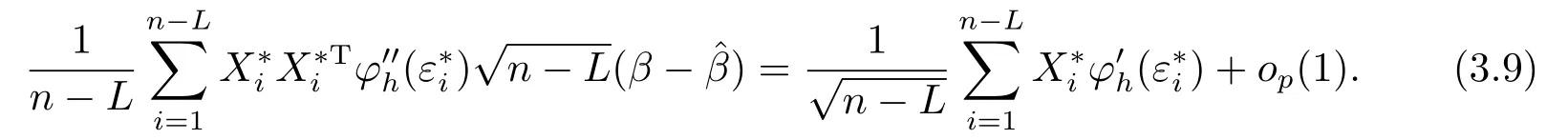
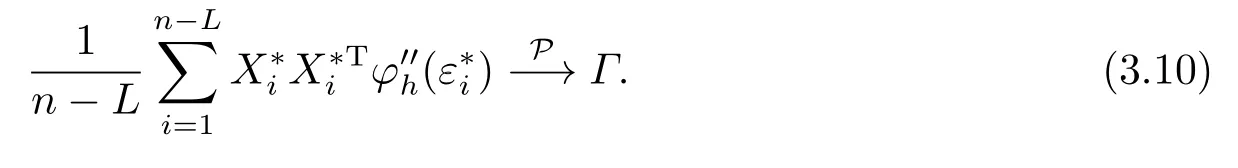
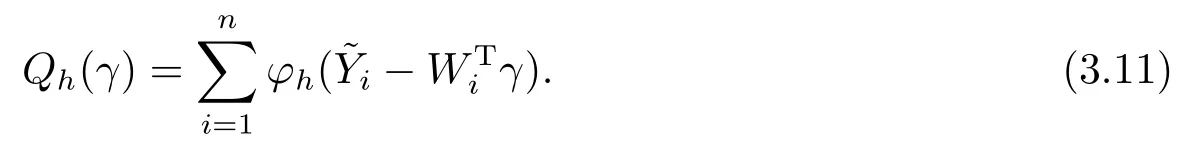
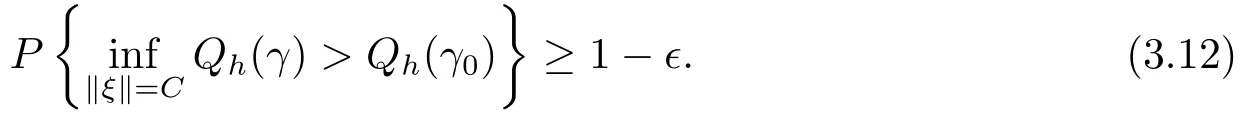



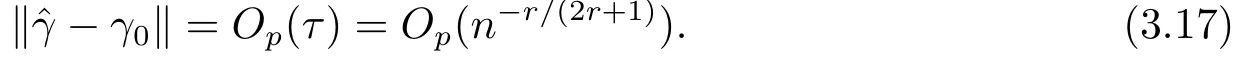
4.模拟研究