军事案例在导数概念教学中的应用

赵静静 火箭军士官学校

导数是高等数学重要基础概念，描述了函数在某点处的变化率。它与物理、几何、经济等学科关系密切，在工程技术和日常生活中也有着广泛的应用。荷兰数学家和数学教育家弗兰登塔尔说“数学是现实的，学生从现实生活中学习数学，再把学习到的数学应用到现实中去”，所以学生的现实经验是其学习数学的基础。教师要善于从学生的经验出发，挖掘学生感兴趣的案例，以学生熟知的军事案例为驱动，提出问题、分析问题，从实际问题中抽象出数学模型，概括数学知识，再用数学知识去解决案例中的实际问题，让知识从生成到应用，形成闭环，让数学“看得见、摸得着、用的上”。

一、教学分析

导数的概念较为抽象，学生不易理解。平面曲线的切线问题是一个几何问题，较为枯燥，同时学生没有应用切线解决实际问题的经验，所以没有学习的兴趣也没有学习的动力。在物理上，物体在某点处的运动方向即为其运动轨迹在该点处的切线。在教学中，从学生的这个实际认知出发，采用贴近部队、贴近装备、贴近实战的坦克爬坡问题，把切线斜率问题结合这个军事背景重新阐述，作为案例进行引入，层层分析，逐步引导学生生成导数的概念。

二、教学实施

（一）问题提出，激发兴趣

最大爬坡角指汽车在满载时的最大爬坡能力，武器装备也有最大爬坡角，已知某型坦克的最大爬坡角为30°。在执行任务时坦克要爬过某个山坡，坦克驾驶员如何预判坦克能否直接爬过山坡？

（二）问题分析，建立模型

坦克能否直接爬过山坡取决于坦克在爬坡过程中的最大倾斜角是否超过30°，若不超过30°坦克就能顺利爬过山坡。建立如图1所示的平面直角坐标系，假设山坡垂直截面的边界曲线方程满足。如图2所示，坦克在任意点处的倾斜角α就是在该点处曲线的切线的倾斜角。而切线切率k= t anα，所以要讨论的问题转换成分析曲线上任意点切线的斜率是否超过。曲线的切线斜率又将如何求解呢？

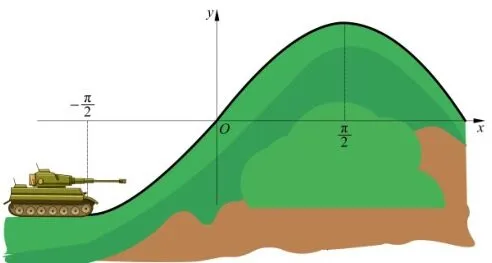
图1 坦克爬坡示意图

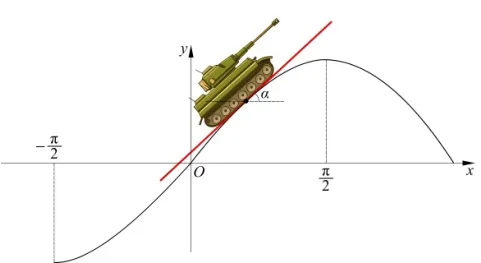
图2 坦克倾斜角

（三）问题探究，生成概念

任取曲线上一点M(x0,y0)，如图3所示，设直线MT为曲线在点M处的切线。两点确定一条直线，直接作出曲线过点M的切线是不能实现的，所以在曲线上另取异于M的一点N作出曲线的割线MN。M、N两点的纵坐标之差为Δy，横坐标之差为Δx，则割线MN的斜率。将割线MN绕点M旋转，随着割点N向点M的无限趋近，Δx的逐渐减小趋近于0，割线MN逐渐趋近于切线MT。因而割线MN的斜率在Δx→0时的极限即为切线MT的斜率，所以

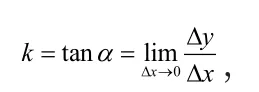
这个极限就称为函数f(x)在x0处的导数，即

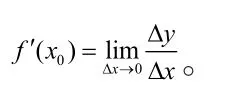
综上分析，函数在某点处的导数即为曲线在该点处切线的斜率，这也称为导数的几何意义。

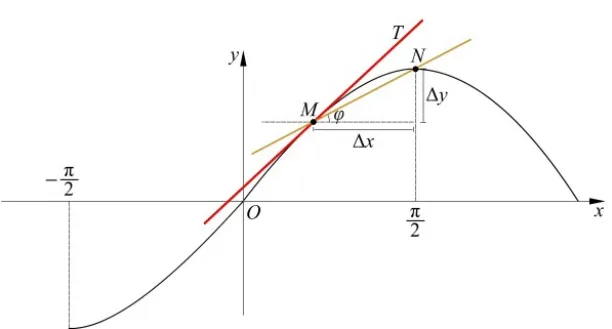
图3 切线

（四）问题解决，回扣引例

根据导数的几何意义，切线上任一点M处的切线即为

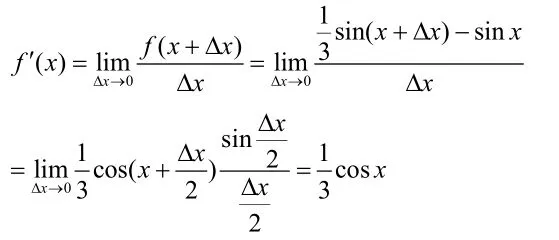
也就是说，坦克在爬坡过程中最大的倾斜角也不会超过30°，所以坦克可以顺利的爬过山坡。

上述问题在解决的过程中先是抽象出了数学问题，让学生感受到数学和生活、工作的密切联系；对数学问题的解决则让学生逐步生成了导数的概念，建立起对导数的几何意义的认识，明确了切线斜率和导数的联系；最终又应用导数的概念解决了坦克爬坡问题。这种应用知识从实际问题中抽象、提炼出数学问题并建立模型的过程就是数学建模。在对军事问题的解决中潜移默化地锻炼了学生的建模能力，提高了其应用数学知识解决实际问题的能力。

三、教学总结

弗兰登塔尔还有一句名言“没有一种数学思想，是以它被发现时的那个样子发表出来”。数学中抽象的概念固然简洁美丽，却掩盖了产生这些概念的实际问题，也掩盖了前人对这些问题所进行的火热的思考。军事案例的教学即是重述这些问题，让学生以这些问题为驱动，重新进行火热的思考，火热思考的积累就是创新思维的源泉，发掘和领会火热思考的能力是学习能力的主要表现。军事案例教学通过对问题的解决，提高了学员的综合能力。