关于CopositivePlus张量及其互补问题的研究
2020-01-09刘康
刘 康
(天津大学数学学院,天津 300350)
0 引 言
随着现代科学技术的发展,张量(超矩阵)作为矩阵的高阶推广,在化学、医学与神经科学、社会网络分析、高光谱图像以及人脸识别等方面都有着广泛应用.张量互补问题(TCP)作为互补问题的一个特定子类,也引起了广泛关注和研究.
有许多文献对TCP解集的理论性质展开研究,包括解的存在性[1-6]、解的全局唯一性[3,7]、解集的有界性[8]和稀疏解的存在性[2]等.Huang和Qi在文献[9]中给出了张量互补问题的一个重要应用,为TCP的进一步研究提供了动力.
在TCP的研究中,结构张量扮演了重要的角色.很多结构张量已经被引入和研究,其中,具有广泛应用的Copositive张量得到了很多研究[10-14],文献[14]中给出了Copositive张量在物理和超图领域的应用.特别地,在文献[15]中,作者对Copositive张量的理论、方法及其应用进行了综述.
在以往关于结构张量的研究中,大多数都是将结构矩阵的概念、相关的理论与方法延伸到张量情况.由于张量远比矩阵复杂,有很多矩阵相关的理论不能延伸到张量情况.在本文中,CopositivePlus矩阵的概念被延伸到高阶张量,即引入了CopositivePlus张量的概念,然后讨论了CopositivePlus张量的性质,以及对应张量互补问题解集的性质.
1 预备知识
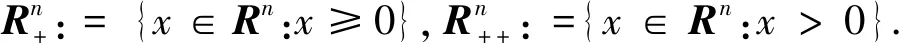
一个m阶n维张量A=(ai1…im)可以看作是元素ai1…im的多重线性排列,其中ij∈{1,2,…,n},j∈{1,2,…,m}.如果张量的元素都为实数,则称该张量为实张量;所有m阶n维实张量的集合记作R[m,n].如果任意置换元素ai1…im的下标i1,…,im,其值保持不变,则张量A=(ai1…im)称为对称张量;如果任意置换元素ai1…im的下标i2,…,im,其值保持不变,则张量A=(ai1…im)称为偏对称张量.
Qi在文献[16]中提出了对称张量特征值的概念,并讨论了相关的性质.从此,掀起了张量谱理论的研究热潮.之后,结构张量、张量互补问题相继引起人们的关注和研究.
对于任意的张量A∈R[m,n]和任意的x∈Rn,Axm-1∈Rn被定义如下:

∀i∈{1,2,…,n}.
对于给定的映射F:Rn→Rn,且q∈Rn,经典互补问题是找到一个x∈Rn使得
x≥0,F(x)+q≥0,xT(F(x)+q)=0.
(1)
本文主要考虑问题(1)在F(x)=Axm-1,A∈R[m,n]的情形.此时问题(1)具体化为
x≥0,Axm-1+q≥0,xT(Axm-1+q)=0,
这被称为张量互补问题,简写为TCP(A,q),记TCP(A,q)的解集为SOL(A,q).
定义1.1[1]称张量A∈R[m,n]是Q张量,当且仅当对于所有q∈Rn,张量互补问题TCP(A,q)有解.
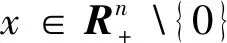
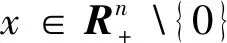
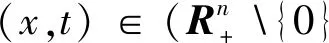
在上式中,如果取t=0,称张量A是R0张量.
2 主要结论
2.1 CopositivePlus张量的性质
定义2.1.1[17]矩阵M称为CopositivePlus的,如果下列条件成立:
(1)x≥0,有xTMx≥0;
(2)x≥0,xTMx=0,有(M+MT)x=0.
引理2.1.1[17]如果一个对称Q矩阵是CopositivePlus的,那么它一定是严格Copositive矩阵.
引理2.1.2[17]如果一个矩阵M是CopositivePlus的,那么下列命题等价:
(A)M∈Q;(B)M∈R;(C)M∈R0.
由定义2.1.1引入CopositivePlus张量的概念.
定义2.1.2假设A∈R[m,n]是一个偏对称张量,则A是CopositivePlus张量当且仅当下列条件成立:

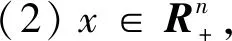
由定义2.1.2、引理2.1.1和引理2.1.2有如下定理:
定理2.1.1假设A∈R[m,n]是一个Q张量,如果A是CopositivePlus的,并且TCP(A,0)有非零解,则A不是严格Copositive张量.


定理2.1.2假设A∈R[m,n]是一个Q张量,并且是CopositivePlus的,如果m≥3,那么A不一定是R张量.
证明:设张量A=(ai1i2i3)∈R2×2×2为一个3阶2维张量,其元素为a111=a211=a122=a222=1,a121=a112=a221=a212=-1.

Ax3=(x1+x2) (x1-x2)2.
由定义2.1.2,知A是CopositivePlus的.首先证明A是Q张量.
假设a,b为任意非负实数,就以下几种情形展开证明.
(1)令q=(a2,b2)T,取x=(0,0)T,显然为TCP(A,q)的解.
(2)令q=(a2,-b2)T,取x=(0,b)T,满足
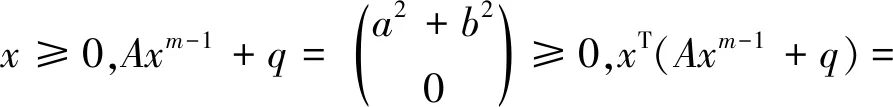
(3)令q=(-a2,b2)T,取x=(a,0)T,满足


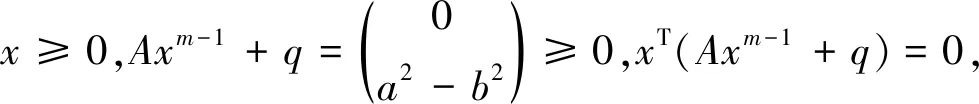
综上,A是Q张量,且A是CopositivePlus的.
另一方面,由q的任意性,取q=(0,0)T,容易验证x*=(1,1)T为解之一,于是有(Ax2)i=0,xi≥0,i=1,2,即x=(1,1)T,t=0为方程组
的解.由定义1.4,可知A不是R张量.
定理2.1.3假设A∈R[m,n]是一个Q张量,且是CopositivePlus的,如果m≥3,那么A不一定是R0张量.
证明:同定理2.1.2,取A=(ai1i2i3)∈R2×2×2为一个元素为a111=a211=a122=a222=1,a121=a112=a221=a212=-1的三阶张量.由定理2.1.2,知A是Q张量且是CopositivePlus的.
由q的任意性,取q=(0,0)T,容易验证x*=(2,2)T也为解之一,可知x=(2,2)T为方程组

的一个解.根据定义1.4,可知A不是R0张量.
2.2 CopositivePlus张量互补问题
基于CopositivePlus矩阵的线性互补问题,Danao[18]证明了其解集的非空有界性,而对于CopositivePlus张量,其相应的张量互补问题未必有界.
首先,本研究将Danao[18]的结论列举如下.
引理2.2.1[18]如果一个Q矩阵是CopositivePlus的,那么它对应的互补问题的解集一定非空有界.
由引理2.2.1,关于张量互补问题,有如下定理:
定理2.2.1假设A∈R[m,n]是一个Q张量,并且是CopositivePlus的,如果m≥3,那么其解集SOL(A,q)不一定有界.
证明:举一个解集无界的例子进行反证.
设张量A=(ai1i2i3)∈R2×2×2为一个3阶2维张量,其元素为a111=a211=a122=a222=1,a121=a112=a221=a212=-1.故有
由定理2.1.2的证明,知A是Q张量且是CopositivePlus的.
另一方面,由q的任意性可知,取q=(0,0)T,此时,对任意满足(t,t)T,t≥0的向量均为张量互补问题的解,故SOL(A,q)无界,结论得证.
根据定理2.2.1,如果A是Q张量且是CopositivePlus的,那么在什么条件下,一定能保证SOL(A,q)非空有界呢?
不妨假设A的每一个元素都为严格正,下面证明此时SOL(A,q)非空有界.
定理2.2.2假设A∈R[m,n]是Q张量,并且是CopositivePlus的,如果其元素严格正,则其解集SOL(A,q)有界.
证明:利用反证法证明该结论的正确性.
首先假设SOL(A,q)无界. 即存在一个非负向量列{xi},i=1,2,…,xi≠0,‖xi‖→∞使得

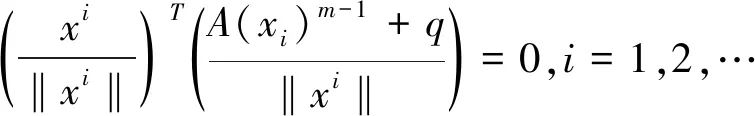
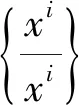
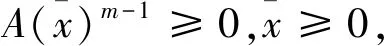
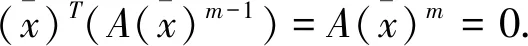

3 总 结
本文给出了CopositivePlus张量的定义,并对这类新定义的结构张量的性质进行了研究.对于张量互补问题解集的研究方面,本文也证明了CopositivePlus张量在为Q张量且每一个元素都为严格正时,它对应的张量互补问题的解集是有界的.当然,CopositivePlus张量作为CopositivePlus矩阵在高阶张量的自然推广,作为Copositive张量的一个子类,具有很好的理论性质,理论上还有很多相应的结论值得延伸和探索.
